It is known that particles in solids liquids

It is known that particles in solids, liquids & gases are in a state of constant motion. Movement in solids, liquids and gases This is called the kinetic theory of matter. In liquids, particles are moving more freely than in solids and in gases they move more freely than in liquids. Particles in a gas such as ammonia (NH 3) spread very quickly through the air in a classroom. This process – of a gas spreading through another gas is called diffusion. This occurs in liquids as well. Motion of molecules in gases 1

All matter consists of minute particles in constant, random motion. In solids, particles are close together & exhibit vibratory motion. In liquids & gases, particles further apart & freer to move. Particles can vibrate, spin & move from place to place. Diffusion can take place. In gases, spaces between particles are large & can thus be compressed. Molecules bump into each other & walls of container – thus creating a pressure that acts in all directions. 2

Molecules in a sample of gas particles all move at different speeds. The average speed of the sample of gas particles remains constant for a certain temperature. Average kinetic energy Ek ∝ T. Particles moving at different speeds, but having the same average Ek. Movement of gas particles 3

Solid – particles close together with vibratory motion Liquid – particles further apart, move more easily & move from point to point in liquid. Exert pressure Gas – particles far apart, move with higher velocities & fill the container with their movement. Exert pressure inside container. 4

Ideal gases are imaginary gases where the particles: Ideal gas always 1. Are identical in all ways obeys gas laws 2. Occupy no volume under all conditions. 3. Exert no forces on each other (except during collisions) 4. Collide with perfectly elastic collisions in which energy is conserved. Gas laws As pressure is increased, volume of an ideal gas can decrease to 0 volume! 5

Real gases deviate from the behaviour of ideal gases at very low temperatures and very high pressures – where they tend to become liquids. Most of the time, real gases behave like ideal gases. The real gases that behave closest to the ideal gas model are He and H 2. Ideal vs real gases 6

In order to fully describe and study a gas, we need to refer to the mass, volume, pressure and temperature of the gas. To see how they relate to one another, we need to keep 2 variables constant and then see how the one changes as we vary the other. 7

You are surrounded by millions of air particles all the time – the atmosphere. They exert a pressure in all directions – even on you! This pressure is called the atmospheric pressure. In view of the fact that this pressure has always been there – you do notice it at all. 8

Using a bicycle pump, pull out the plunger, put your finger over the hole at the bottom & then push the plunger in as far as you can. Pressure, volume & temperature As the pressure increases, so the volume decreases because the same number of particles are now in a more confined space & they are bumping each other & the walls of the container more frequently – resulting in an increased pressure in the pump. 9 Double the pressure is experienced when vol. is halved.

The unit of pressure is the pascal (Pa). 1 Pa occurs when 1 N acts on 1 m 2 surface area. This is a small value & we usually use kilopascals (k. Pa) instead. 1 k. Pa = 1000 Pa. Atmospheric pressure is 100 k. Pa at sea level. A Bourdon gauge is used to measure gas pressure. How gauge works Bourdon gauge 10

Robert Boyle 1627 -1691 The apparatus is used to inves- Volume vs pressure tigate the relationship between p and V for a fixed number of moles of a gas at a 11 constant temperature.

Air trapped in tube A. Air causes increased pressure. Bourdon guage. Air pumped in. Oil reservoir. 12

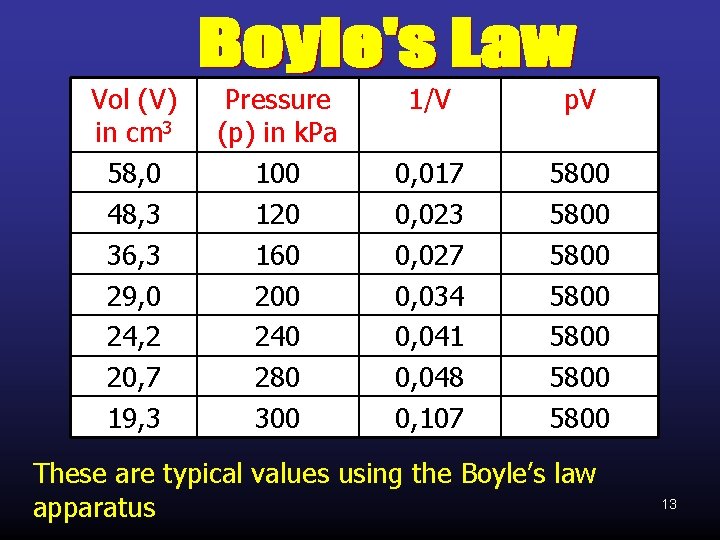
Vol (V) in cm 3 58, 0 48, 3 36, 3 29, 0 24, 2 20, 7 19, 3 Pressure (p) in k. Pa 100 120 160 200 240 280 300 1/V p. V 0, 017 0, 023 0, 027 0, 034 0, 041 0, 048 0, 107 5800 5800 These are typical values using the Boyle’s law apparatus 13

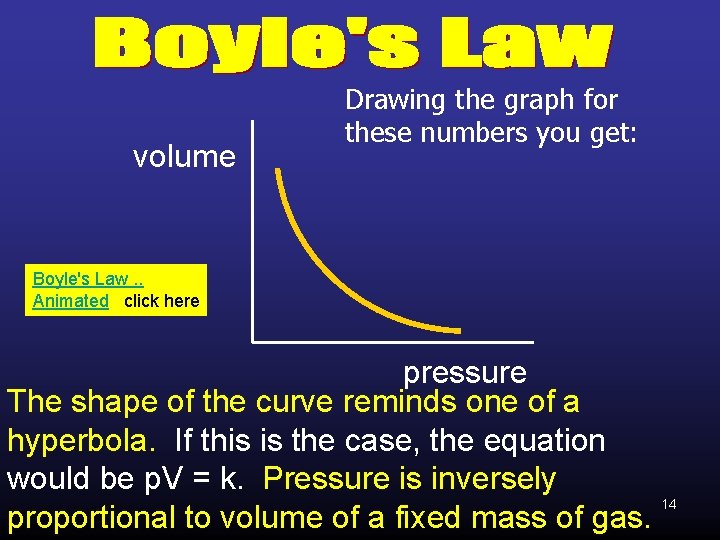
volume Drawing the graph for these numbers you get: Boyle's Law. . Animated click here pressure The shape of the curve reminds one of a hyperbola. If this is the case, the equation would be p. V = k. Pressure is inversely 14 proportional to volume of a fixed mass of gas.

As the curve could be something other than a hyperbola, we can check as follows: If p. V = k V = 1/ p k A graph of V vs 1/p would therefore indicate a straight line through the origin (compare y = mx). As a straight line is obtained it means the original graph was a hyperbola therefore 15 p. V = k.

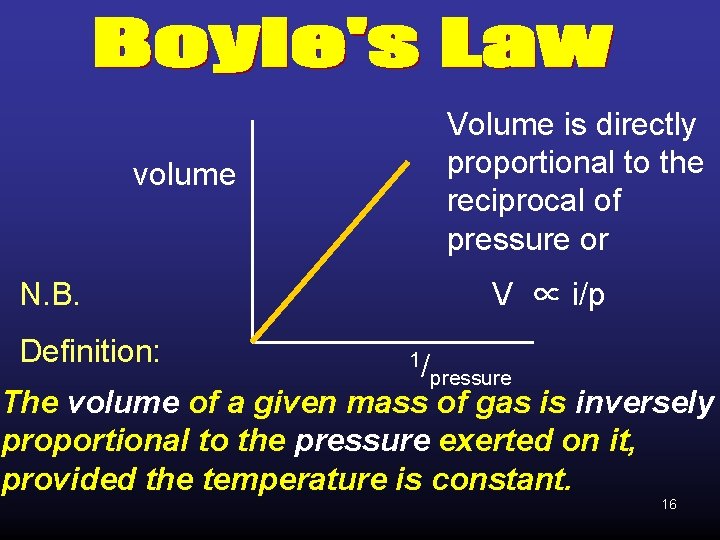
Volume is directly proportional to the reciprocal of pressure or volume N. B. Definition: V ∝ i/p 1/ pressure The volume of a given mass of gas is inversely proportional to the pressure exerted on it, provided the temperature is constant. 16

From the defining relationship between pressure and volume, we get the equation derived from this relationship: Since p 1 V 1 = k and p 2 V 2 = k then: p 1 V 1 = p 2 V 2 Boyle’s law equation. 17

Take note that the conditions for Boyle’s law stated in the previous formulation are: 1. The quantity of gas remains constant. 2. The temperature remains constant. If p. V = k, what would the unit of measurement for k be? Explain the answer in terms of the units of measurement for p and V. Relationship P, V & T 18

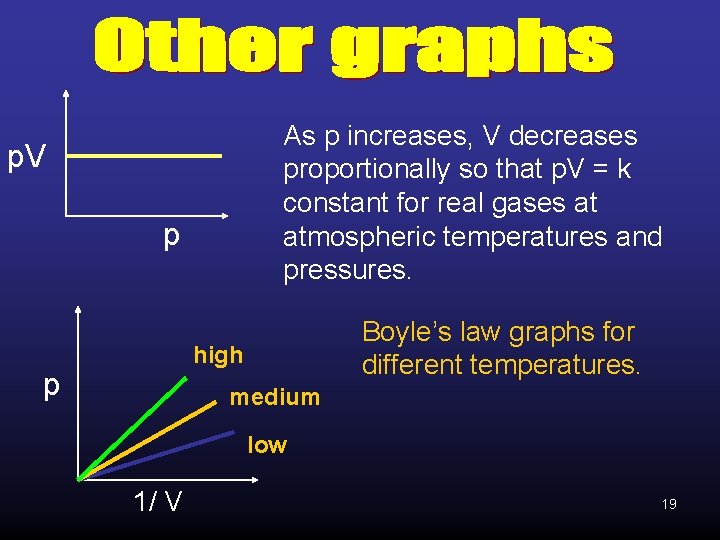
As p increases, V decreases proportionally so that p. V = k constant for real gases at atmospheric temperatures and pressures. p. V p Boyle’s law graphs for different temperatures. high p medium low 1/ V 19

What happens when a cannon is fired? The exploding gunpowder causes the gas to expand rapidly and thrust the cannon ball into the air at high velocity. This principle can be used in rockets, car engines, power station turbines & hot air balloons. 20

Drop of Hg in capillary tube Ruler Thermometer Ice cubes Air trapped in tube Record the volume of the air column below the Hg as the temperature rises & record the values. As the temperature increases, so the volume also increases & we need to study this relationship between volume & temperature. This is known as Charles’ law of volume. 21

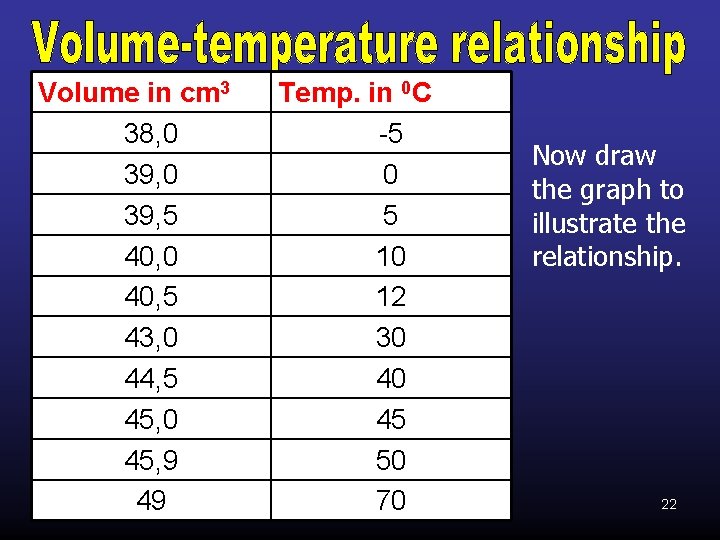
Volume in cm 3 38, 0 39, 5 40, 0 40, 5 43, 0 44, 5 45, 0 45, 9 49 Temp. in 0 C -5 0 5 10 12 30 40 45 50 70 Now draw the graph to illustrate the relationship. 22

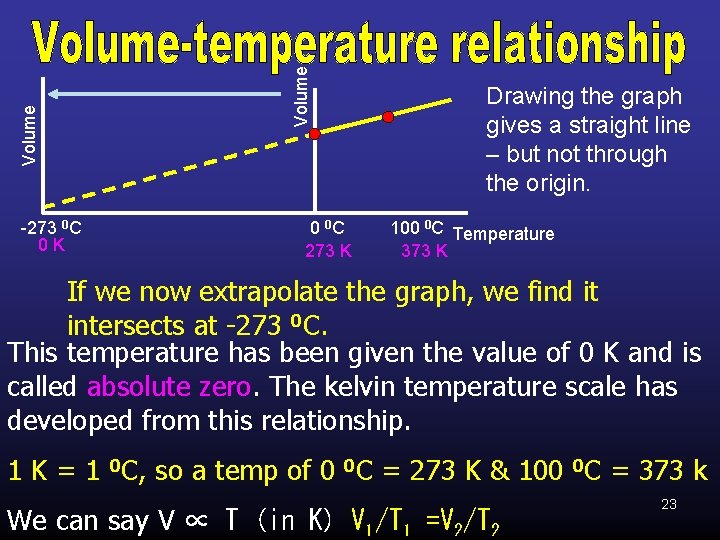
Volume -273 0 C 0 K 0 0 C 273 K Drawing the graph gives a straight line – but not through the origin. 100 0 C Temperature 373 K If we now extrapolate the graph, we find it intersects at -273 0 C. This temperature has been given the value of 0 K and is called absolute zero. The kelvin temperature scale has developed from this relationship. 1 K = 1 0 C, so a temp of 0 0 C = 273 K & 100 0 C = 373 k We can say V ∝ T (in K) V 1/T 1 =V 2/T 2 23

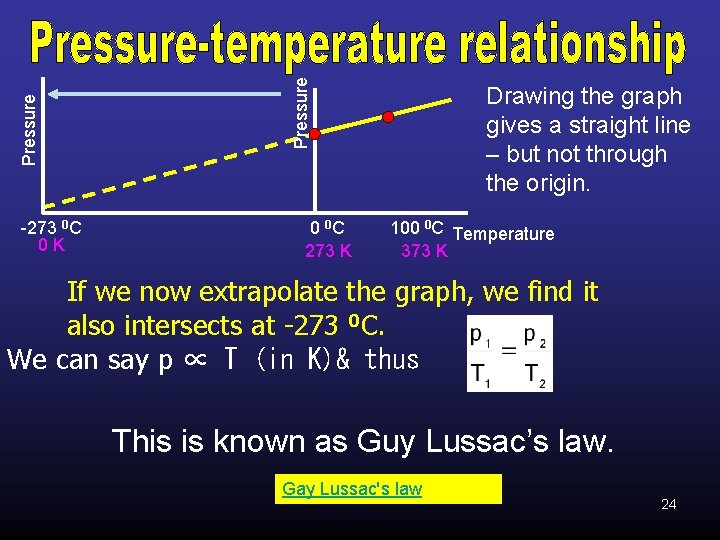
Pressure -273 0 C 0 K 0 0 C 273 K Drawing the graph gives a straight line – but not through the origin. 100 0 C Temperature 373 K If we now extrapolate the graph, we find it also intersects at -273 0 C. We can say p ∝ T (in K)& thus This is known as Guy Lussac’s law. Gay Lussac's law 24

Lord William Thomson Kelvin 1824 -1907 V 1 T 1 V 2 = T 2 From this relationship we get the above equation. P T V relationships Combining the p-V, the p-T and the V-T relationships, we then get: p 1 V 1 = p 2 V 2 PV&T Charles and Gay-Lussac's Law – Animated click here T 1 T 2 This is known as the general gas equation. 25 N. B. v & P may be in any units, but T must be in kelvin.

To convert one temperature to the other – or vice -versa, we use the following equation: Temp in kelvin = 273 + temp in celsius T = 273 + t A temp of – 50 0 C is thus: Conversion of Celcius to Kelvin temperatures T = 273 + (-50 0 C) = 223 K Now try converting the following: 20 0 C 150 0 C 70 K 200 K 26

When describing a gas, sometimes we refer to S. T. P. This is standard temperature & pressure. These standard conditions are: Standard pressure = 100 k. Pa & (1 Atm pressure) Standard temperature = 0 0 C or 273 K Now try some problems & calculations on the gas laws. Molecular Model for an Ideal Gas Special processes of an ideal gas click here 27

We can combine the 3 gas law equations and get the following ideal gas law equation: p. V = n. RT Pressure must be in pascals Volume in m 3 & Temperature in kelvin (K) The universal gas constant (R) has the value of 8, 31 J∙K-1∙mol-1 28

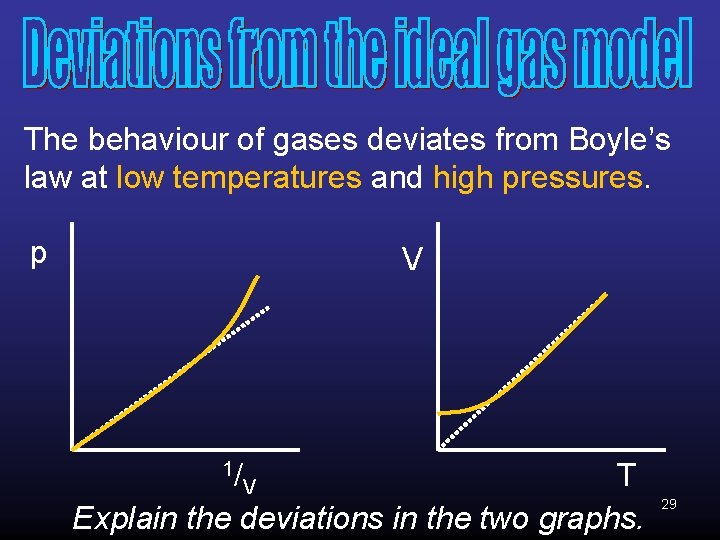
The behaviour of gases deviates from Boyle’s law at low temperatures and high pressures. p V 1/ T Explain the deviations in the two graphs. V 29

p 1 T 1 and p 2 T 2 p p 1/T 1 = p 2/T 2 0 T Explain the deviation above. 30

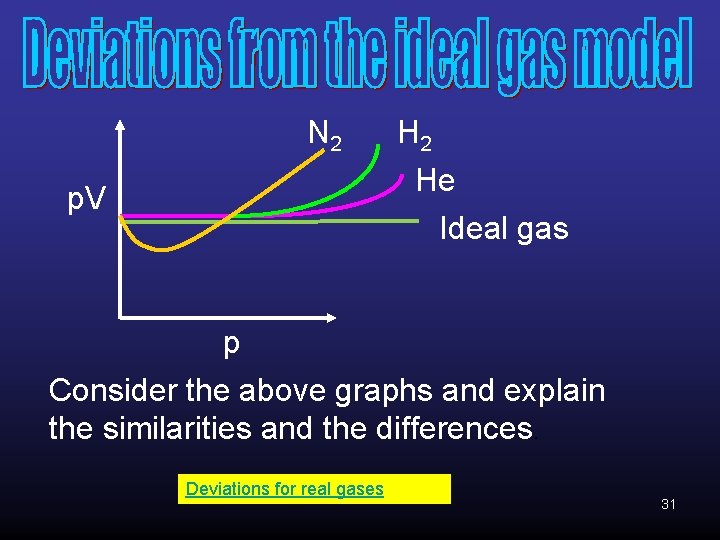
N 2 He Ideal gas p. V p Consider the above graphs and explain the similarities and the differences. Deviations for real gases 31