IT 105 Matematika Diskrit Logika Pernyataan Penghubung Pernyataan

IT 105 Matematika Diskrit Logika (Pernyataan & Penghubung Pernyataan) Grace Lusiana Beeh, S. Kom. lezzz. mail@gmail. com Selasa, 17 Jan 2012

Presentasi Mat. Dis - Grace Beeh - 2012 LOGIKA

Presentasi Mat. Dis - Grace Beeh - 2012 LOGIKA Logika merupakan studi penalaran (reasoning). Dalam Kamus Besar Bahasa Indonesia disebutkan definisi penalaran : cara berpikir dengan mengembangkan sesuatu berdasarkan akal budi bukan dengan perasaan atau pengalaman. Materi logika difokuskan pada hubungan antara pernyataan-pernyataan (statements).

Presentasi Mat. Dis - Grace Beeh - 2012 Ilmu Logika Ilmu logika berhubungan dengan kalimat (argumen-argumen) dan hubungan yang ada di antara kalimat tersebut. Tujuannya : memberikan aturan sehingga orang dapat menentukan nilai kebenaran suatu kalimat.

Presentasi Mat. Dis - Grace Beeh - 2012 Fungsi Logika dalam Metematika menspesifikasikan matematis. makna dari pernyataan untuk membedakan antara argumen yang valid dan tidak valid. untuk membuktikan teorema-teorema di dalam matematika.

Presentasi Mat. Dis - Grace Beeh - 2012 Penerapan Logika Matematika Logika mempunyai aplikasi yang luas di dalam ilmu komputer : dalam bidang pemrograman, analisis kebenaran algoritma, kecerdasan buatan (artificial intelligence), perancangan komputer, kemanan jaringan (enkripsi) dll

Presentasi Mat. Dis - Grace Beeh - 2012 PERNYATAAN

Presentasi Mat. Dis - Grace Beeh - 2012 Pernyataan Nama Lain : Kalimat Deklaratif atau Proposisi Pernyataan adalah suatu argumen/statemen/kalimat yang bernilai benar atau salah, dan tidak keduanya. Pernyataan adalah kalimat yang mempunyai nilai kebenaran (T/F).

Presentasi Mat. Dis - Grace Beeh - 2012 … Semarang 1 adalah ibokota Jawa Tengah. adalah bilangan prima. Dika 1+1 mempunyai mobil mewah. = 10 Siapa nama Anda?

Presentasi Mat. Dis - Grace Beeh - 2012 … Semarang adalah ibokota Jawa Tengah. (penyataan, True) 1 adalah bilangan prima. (penyataan, False) Dika mempunyai mobil mewah. (bukan pernyataan) 1+1 = 10 (pernyataan, jika biner True ; jika desimal False) Siapa nama Anda? (bukan pernyataan)

Presentasi Mat. Dis - Grace Beeh - 2012 Proposisi? Siapa nama adik saya? x + y = 12 2 mencintai 3. A lebih pandai dari B. Cecep sepeda boleh meja. Jika bukan proposisi, mengapa?

Presentasi Mat. Dis - Grace Beeh - 2012 PENGHUBUNG PERNYATAAN

Presentasi Mat. Dis - Grace Beeh - 2012 Penghubung Pernyataan Ingkaran/Negasi Konjungsi Disjungsi Implikasi Biimplikasi

Presentasi Mat. Dis - Grace Beeh - 2012 Contoh pernyataan P : Matematika Diskrit itu sulit Q : Saya pandai.

Presentasi Mat. Dis - Grace Beeh - 2012 PENGHUBUNG PERNYATAAN …negasi…

Presentasi Mat. Dis - Grace Beeh - 2012 Ingkaran/Negasi (tidak, bukan) Notasi: Negasi ¬ , ~, ¯, ’ pernyataan P adalah suatu pernyataan ~P yang mempunyai nilai kebenaran berlawanan dari nilai kebenaran pernyataan semula.

Presentasi Mat. Dis - Grace Beeh - 2012 Contoh negasi P : Matematika Diskrit itu sulit. Q : Saya pandai. Pernyataan NOT dari P dan Q: ~P : Matematika Diskrit itu tidak sulit. ~Q : Saya tidak pandai.

Presentasi Mat. Dis - Grace Beeh - 2011 PENGHUBUNG PERNYATAAN …konjungsi…

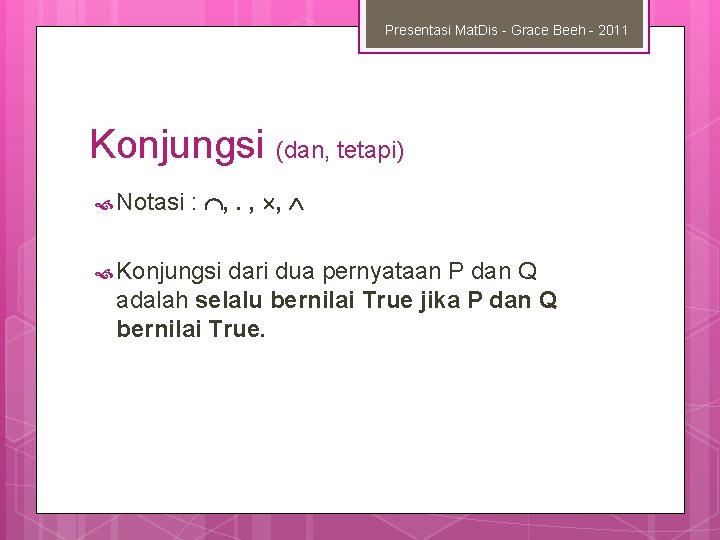
Presentasi Mat. Dis - Grace Beeh - 2011 Konjungsi (dan, tetapi) Notasi : , . , , Konjungsi dari dua pernyataan P dan Q adalah selalu bernilai True jika P dan Q bernilai True.

Presentasi Mat. Dis - Grace Beeh - 2011 Contoh Konjungsi P : Matematika Diskrit itu sulit. (T) Q : Saya pandai. (F) Pernyataan P ^ Q: Matematika Diskrit itu sulit dan/tetapi saya pandai. P ^ Q = T ^ F = F

Presentasi Mat. Dis - Grace Beeh - 2011 Sifat dan Negasi dari Konjungsi simetri: P Q = Q P. Negasi P Q adalah ~P ~Q. Sifat

Presentasi Mat. Dis - Grace Beeh - 2011 … Mawar berwarna merah dan kucing berwarna hitam. “dan” digunakan seperti yang dimaksud simbol ). Prinsip simetri berlaku. P Q = Q P Inem membuka pintu dan berjalan masuk. “dan” berarti “kemudian” karena “berjalan masuk” terjadi setelah “Inem membuka pintu” tidak dapat diterjemahkan dengan . Prinsip simetri tidak berlaku. P Q Q P Inem dan Ponim bersaudara. “dan” bukan penghubung, karena hanya satu kalimat bukan dua kalimat setara yang dihubungkan dengan AND. Bila dipecah, akan menjadi kalimat berita tidak lengkap. “Inem bersaudara”. Kalimat menjadi tidak lengkap karena bersaudara dengan siapa? .

Presentasi Mat. Dis - Grace Beeh - 2011 PENGHUBUNG PERNYATAAN …disjungsi…

Presentasi Mat. Dis - Grace Beeh - 2011 Disjungsi (atau) Notasi: , + , Disjungsi dari dua pernyataan P dan Q adalah bernilai True jika salah satu dari P dan Q, atau keduanya bernilai True.

Presentasi Mat. Dis - Grace Beeh - 2011 Contoh Disjungsi P : Matematika Diskrit itu sulit. (T) Q : Saya pandai. (F) Pernyataan P V Q: Matematika Diskrit itu sulit atau saya pandai. P V Q = T V F = T

Presentasi Mat. Dis - Grace Beeh - 2011 Sifat dan Negasi dari Disjungsi simetri: P Q = Q P. Negasi P Q adalah ~P ~Q. Sifat

Presentasi Mat. Dis - Grace Beeh - 2011 … Saya akan menonton pertandingan di tv atau pergi ke lapangan pertandingan. “atau” dipakai dalam bentuk yang eksklusif untuk memilih salah satu dari dua alternatif tetapi tidak keduanya (P atau Q saja tetapi tidak P dan Q). Ada sesuatu yang salah dengan bolam itu atau dengan pengabelannya. “atau” dipakai dalam bentuk yang inklusif yaitu bisa salah satu atau kedua alternatif terjadi (P, atau Q atau P dan Q). “atau” digunakan seperti yang dimaksud (simbol ). Dua atau tiga orang cedera dalam kecelakaan itu. “atau” tidak ditujukan dalam arti Penghubung yang dimaksudkan tetapi mengenai jumlah orang dalam kejadian itu.

Presentasi Mat. Dis - Grace Beeh - 2012 PENGHUBUNG PERNYATAAN …implikasi…

Presentasi Mat. Dis - Grace Beeh - 2012 Implikasi (jika…. maka…. ) Notasi: Jika P dan Q adalah dua pernyataan, maka implikasi pernyataan P Q dapat dibaca sebagai IF P, THEN Q. P dan Q adalah suatu pernyataan conditional. Untuk : P Q P : hipotesa/antecedent/premis/kondisi/syarat cukup Q : kesimpulan/consequent/konklusi/syarat perlu

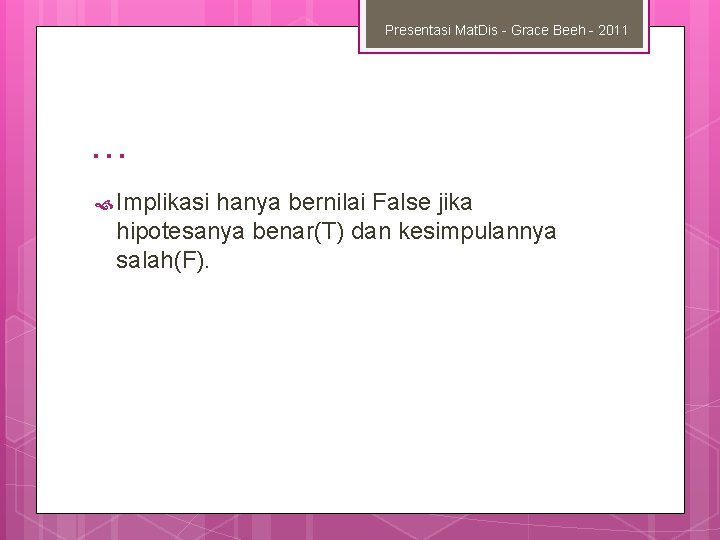
Presentasi Mat. Dis - Grace Beeh - 2011 … Implikasi hanya bernilai False jika hipotesanya benar(T) dan kesimpulannya salah(F).

Presentasi Mat. Dis - Grace Beeh - 2011 Contoh Implikasi P : Saya naik kelas(T) Q : Saya dibelikan sepeda oleh ortu(T) Pernyataan P Q: Jika saya naik kelas maka saya dibelikan sepeda oleh ortu. P Q = T T = T

Presentasi Mat. Dis - Grace Beeh - 2011 Sifat dan Negasi dari Implikasi tidak mempunyai sifat simetri dalam arti bahwa P Q tidak sama dengan Q P. P Q (ekuivalen dengan) ~P Q (P Q) adalah ~(P Q) ~(~P Q) P ~Q Negasi

Presentasi Mat. Dis - Grace Beeh - 2011 … p q memainkan peranan penting dalam penalaran. Implikasi ini tidak hanya diekspresikan dalam pernyataan standard “jika p, maka q” tetapi juga dapat diekspresikan dalam berbagai cara, antara lain: Implikasi Jika p, maka q Jika p, q p mengakibatkan q q jika p p hanya jika q p syarat cukup agar q q syarat perlu bagi p q bilamana p

Presentasi Mat. Dis - Grace Beeh - 2012 PENGHUBUNG PERNYATAAN …biimplikasi…

Presentasi Mat. Dis - Grace Beeh - 2012 Biimplikasi (…. jika dan hanya jika…. ) Notasi: Jika P dan Q adalah dua pernyataan, maka biimplikasi pernyataan P Q (dibaca P jika dan hanya jika Q) mempunyai nilai T bilamana baik P dan Q keduanya mempunyai nilai kebenaran yang sama.

Presentasi Mat. Dis - Grace Beeh - 2012 Contoh Biimplikasi P : Hari cerah (T) Q : Saya pergi ke pantai (T) Pernyataan P Q: Hari cerah jika dan hanya jika saya pergi ke pantai. P Q = T T = T

Presentasi Mat. Dis - Grace Beeh - 2012 Sifat dan Ekuivalensi dari Biimplikasi P Q mempunyai sifat simetri yaitu: P Q = Q P. P Q (P Q) ^ (Q P)

Presentasi Mat. Dis - Grace Beeh - 2011 … Terdapat sejumlah cara untuk menyatakan bikondisional p q dalam kata-kata, yaitu: p jika dan hanya jika q. p adalah syarat perlu dan cukup untuk q. Jika p maka q, dan sebaliknya.

Presentasi Mat. Dis - Grace Beeh - 2012 … Proposisi 1 majemuk berikut adalah bi-implikasi: + 1 = 2 jika dan hanya jika 2 + 2 = 4. Syarat cukup dan syarat perlu agar hari hujan adalah kelembaban udara tinggi. Jika anda orang kaya maka anda mempunyai banyak uang, dan sebaliknya.

Presentasi Mat. Dis - Grace Beeh - 2012 usai

Presentasi Mat. Dis - Grace Beeh - 2012 Tugas Kelas Buatlah 3 pernyataan tunggal. Misalkan ketiga pernyataan itu adalah A, B, C. Kerjakan dalam kalimat untuk: 1. 2. 3. 4. 5. 6. AVB^C ~(A V B) ^ C C ~B A ^ (B C) (A V B) (C v ~A) (A V B) ~(C v A) Buatlah tabel kebenaran dari poin 1 -6 di atas.