IST 4 Information and Logic Office hours moved

IST 4 Information and Logic

Office hours moved from Moore 331 to MQ 1 grades SFL emailed were please let the TAs know if you submitted MQ 1 and did not get the email

IST 4: Planned Schedule – Spring 2014 T = today x= hw#x out x= hw#x due oh = office hours mon tue wed thr 31 M 1 1 7 oh 14 oh 21 oh 28 oh 5 Mx= MQx out 12 oh Mx= MQx due 19 oh 1 T M 2 3 3 4 oh 5 2 M 2 2 midterms oh oh 26 2 oh M 1 fri oh 4 5 oh

Memory MQ 2 Deadline Thursday 4/29/2014 at 10 pm • You are invited to write short essay on the topic of the Magenta Question. • Recommended length is 3 pages (not more) • Submit the essay in PDF format to ta 4@paradise. caltech. edu file name lastname-firstname. pdf • No collaboration. No extensions Grading of MQ: 3 points (out of 103) 50% for content quality, 50% for writing quality Some students will be given an opportunity to give a short presentation for up to 3 additional points

Building Blocks finite number of different parts ‘infinitely’ many structures Natural language: the composition of a small number of parts (letters/words) results in infinitely many conceptual structures Any language: from parts to systems life, biology, music, art, physics, chemistry, computing, engineering, mathematics, literature. . .

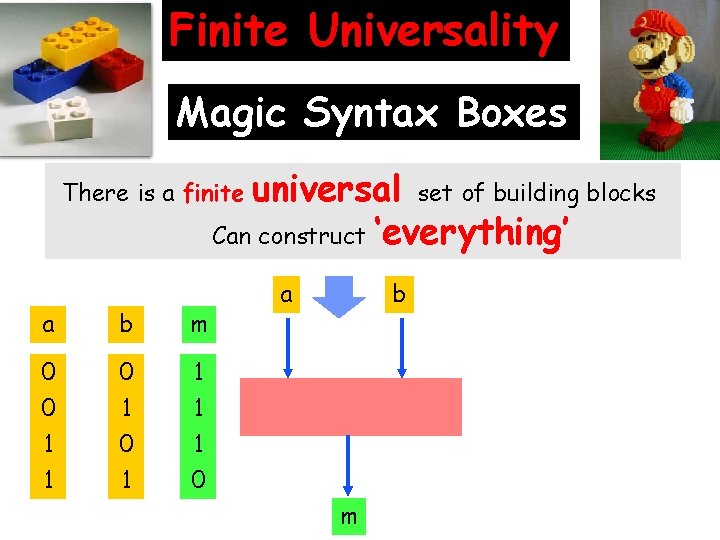
The most important idea in Information Finite Universality of a Language Can construct ‘everything’ from a finite set of building blocks

Finite Universality Magic Syntax Boxes universal set of building blocks Can construct ‘everything’ There is a finite a b m 0 0 1 1 0 a b m

Magic Syntax Boxes Proof by induction: Base: Can generate all the s-boxes of size 2 – a single variable: 0 0 1 1 0 1 Assume true for all s-boxes with n-1 variables Prove true for any s-box with n variables

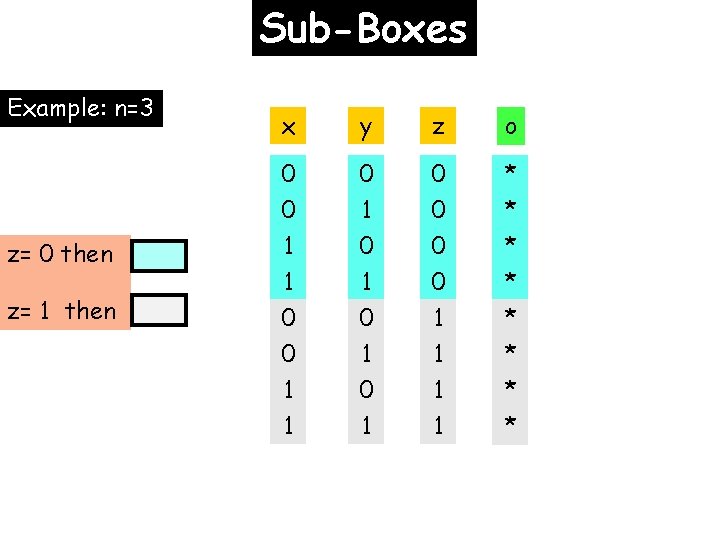
Sub-Boxes Example: n=3 z= 0 then z= 1 then x y z o 0 0 1 0 0 * * * 1 0 0 1 1 1 0 1 0 1 1 * * *

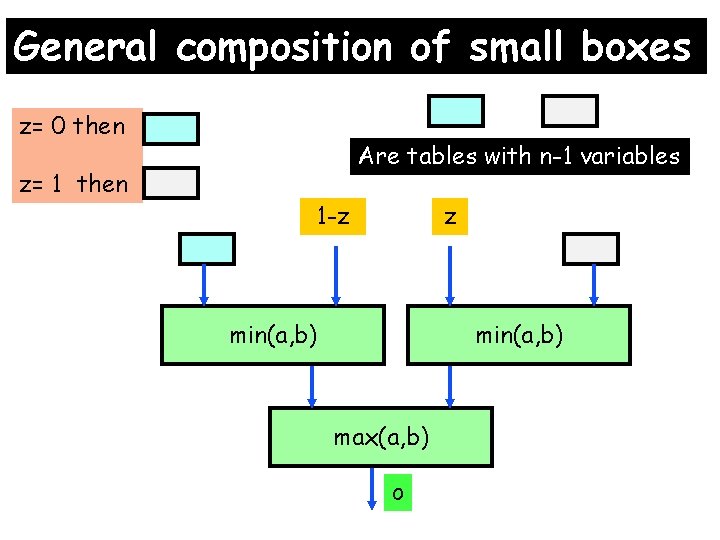
General composition of small boxes z= 0 then z= 1 then Are tables with n-1 variables 1 -z z min(a, b) max(a, b) o

Questions about building blocks? Feasibility Given a set of building blocks: What can/cannot be constructed?

solving equations Can the solutions be expressed using

solving equations Leonardo Fibonacci 1170 -1250 Considered: Found an approximate solution base-60. . Source: wikipedia

solving equations Scipione del Ferro 1465 -1526 Considered: Found a general solution. . . Did not publish it. . . The power of keeping a secret. ? Source: wikipedia

solving equations Niccolò Tartaglia 1500 -1557 Gerolamo Cardano 1501 - 1576 Lodovico Ferrari 1522 – 1565 Will be posted on the class website Source: wikipedia

solving equations Niels Abel 1802 -1826 This activity led to the invention of complex numbers, group theory, abstract algebra. . Source: wikipedia

Arithmetic Boxes

0 1 2 3 4 5 6 7 8 9 0 0 1 2 3 4 5 6 7 8 9 10 2 2 3 4 5 6 7 8 9 10 11 3 3 4 5 6 7 8 9 10 11 12 4 4 5 6 7 8 9 10 11 12 13 5 5 6 7 8 9 10 11 12 13 14 6 6 7 8 9 10 11 12 13 14 15 7 7 8 9 10 11 12 13 14 15 16 8 8 9 10 11 12 13 14 15 16 17 9 9 10 11 12 13 14 15 16 17 18

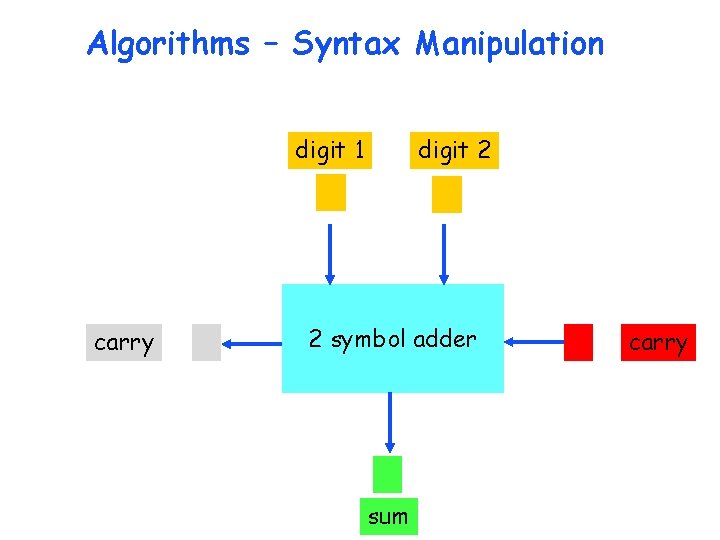
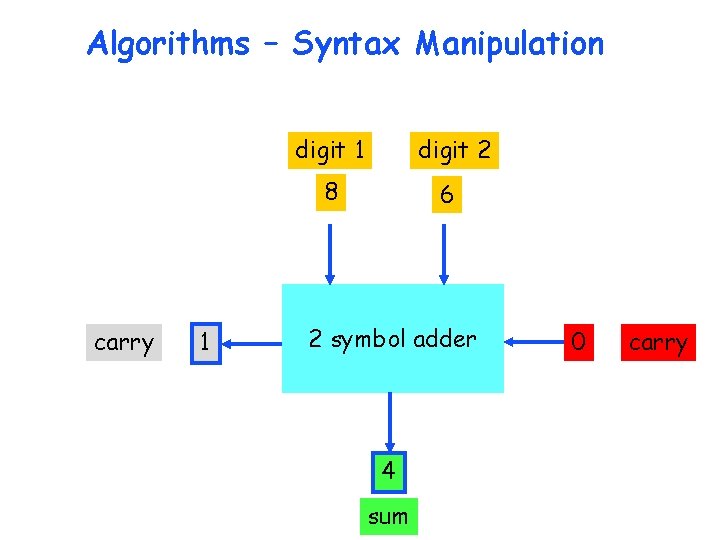
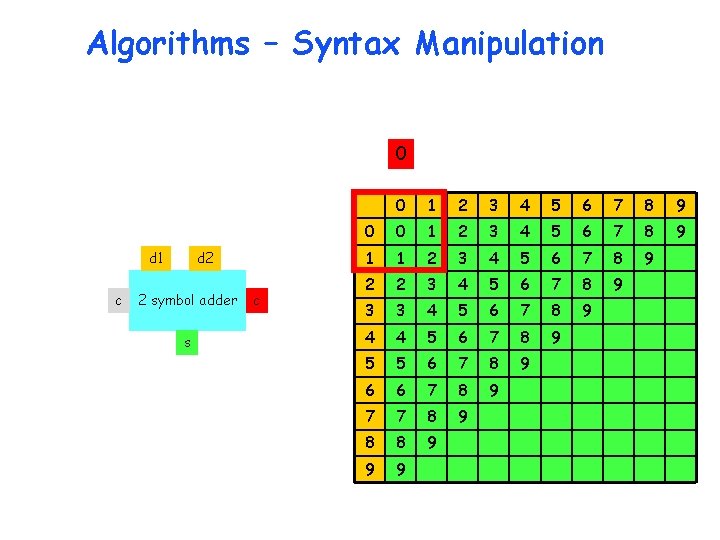
Algorithms – Syntax Manipulation digit 1 carry digit 2 2 symbol adder sum carry

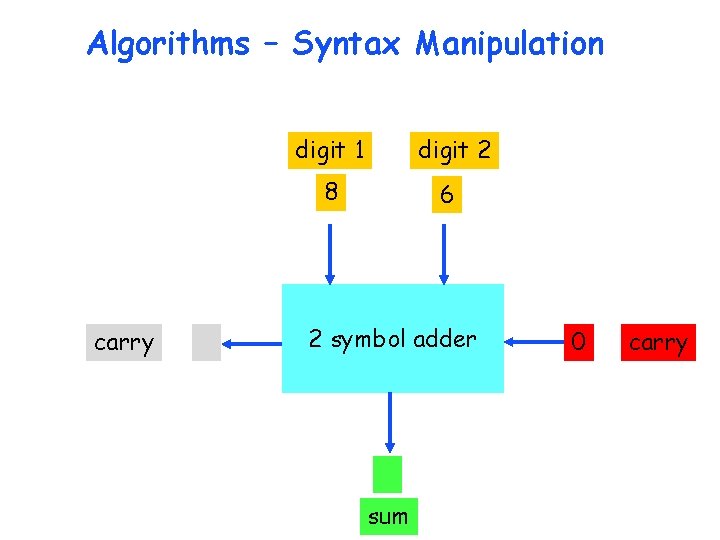
Algorithms – Syntax Manipulation digit 1 digit 2 8 carry 6 2 symbol adder sum 0 carry

Algorithms – Syntax Manipulation digit 1 digit 2 8 carry 1 6 2 symbol adder 4 sum 0 carry

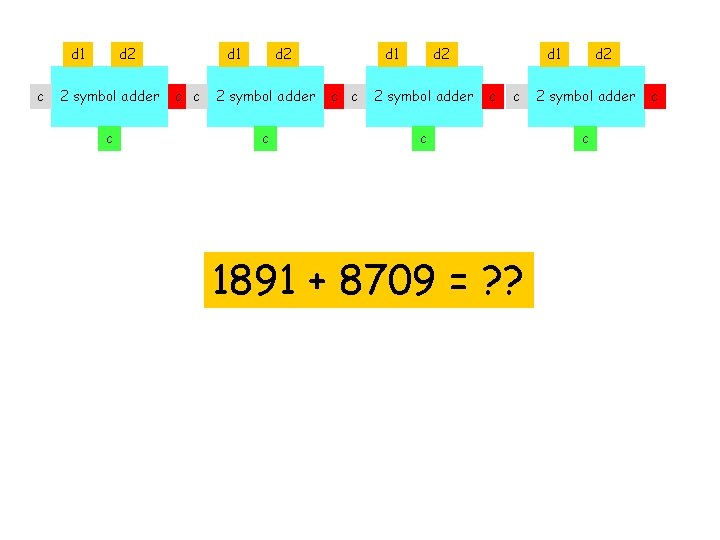
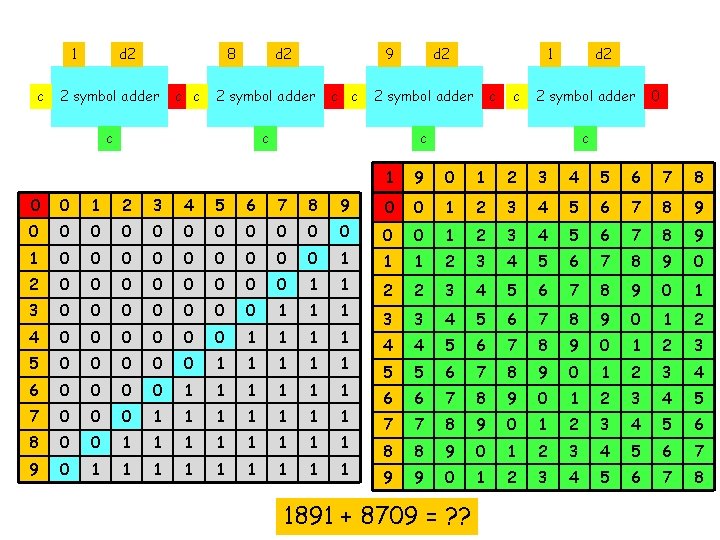
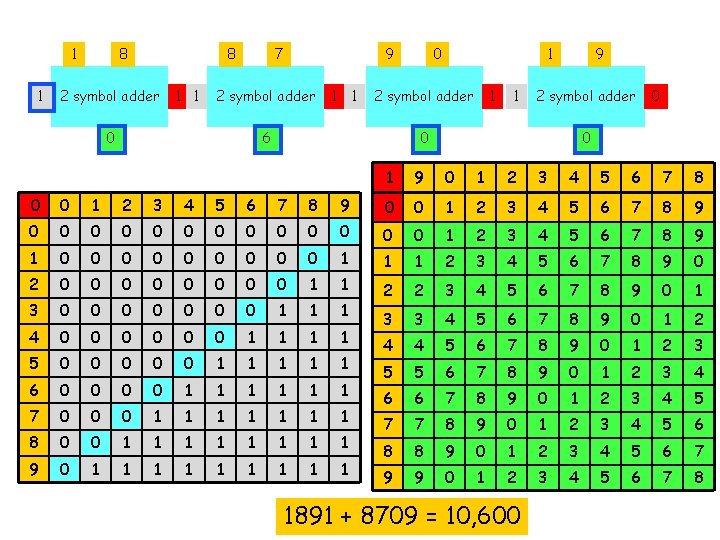
d 1 c d 2 2 symbol adder c d 1 c c d 2 2 symbol adder d 1 c c c 1891 + 8709 = ? ? d 2 2 symbol adder c c

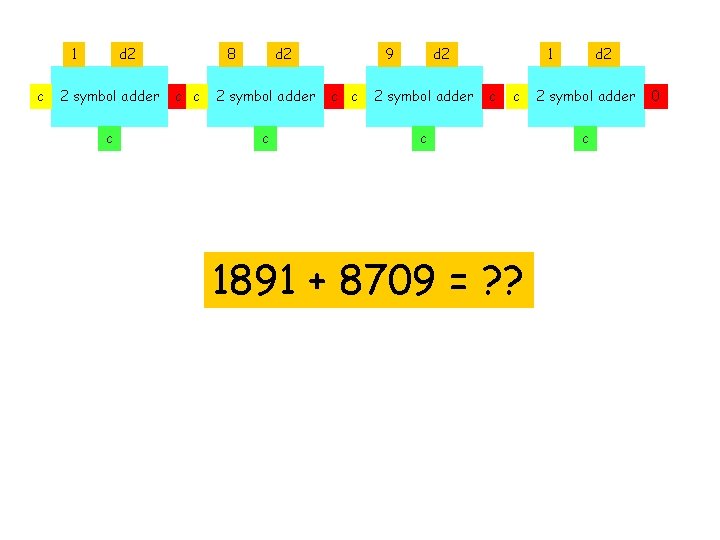
1 c d 2 2 symbol adder c 8 c c d 2 2 symbol adder c 9 c c d 2 2 symbol adder 1 c c c 1891 + 8709 = ? ? d 2 2 symbol adder c 0

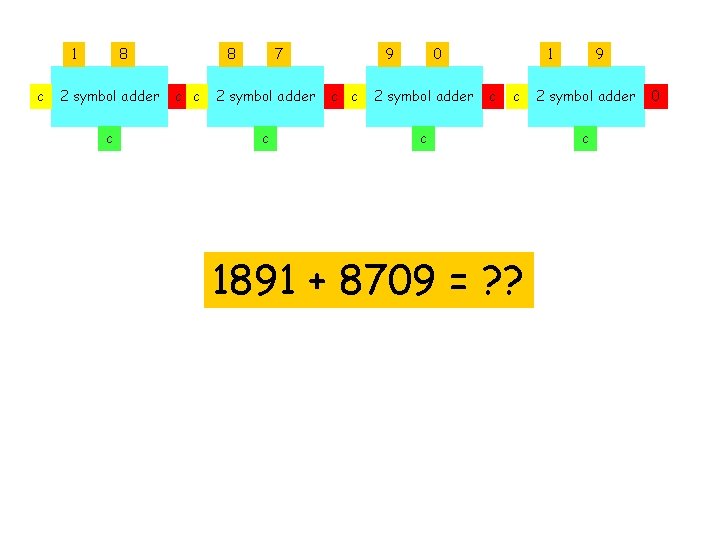
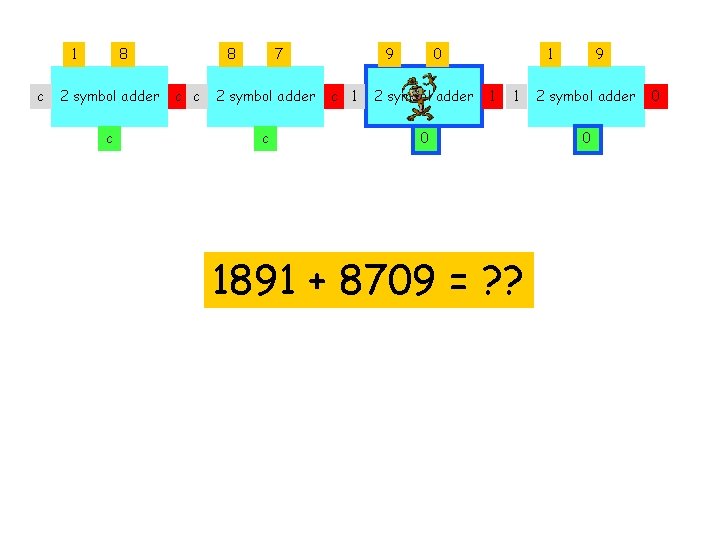
1 c 8 2 symbol adder c 8 c c 7 2 symbol adder c 9 c c 0 2 symbol adder 1 c c c 1891 + 8709 = ? ? 9 2 symbol adder c 0

1 c 8 2 symbol adder c 8 c c 7 2 symbol adder c 9 c c 0 2 symbol adder 1 c 1891 + 8709 = ? ? 9 2 symbol adder 0 0

1 c 8 2 symbol adder c 8 c c 7 2 symbol adder c 9 c 1 0 2 symbol adder 1 1 1 0 1891 + 8709 = ? ? 9 2 symbol adder 0 0

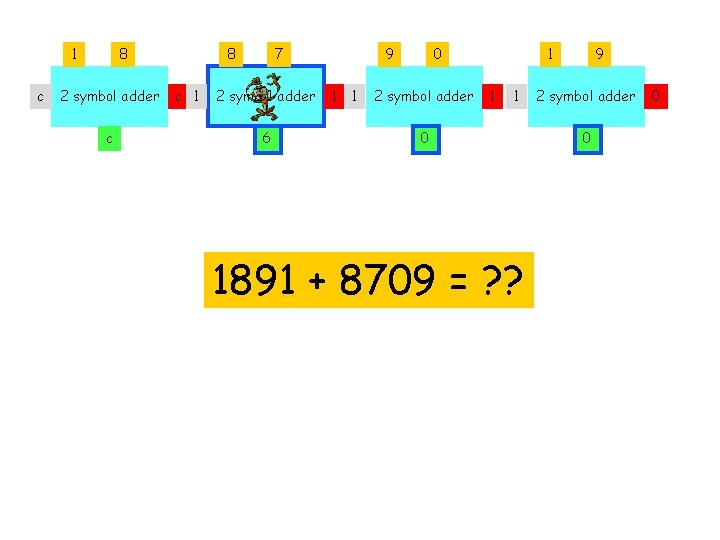
1 c 8 2 symbol adder c 8 c 1 7 2 symbol adder 6 9 1 1 0 2 symbol adder 1 1 1 0 1891 + 8709 = ? ? 9 2 symbol adder 0 0

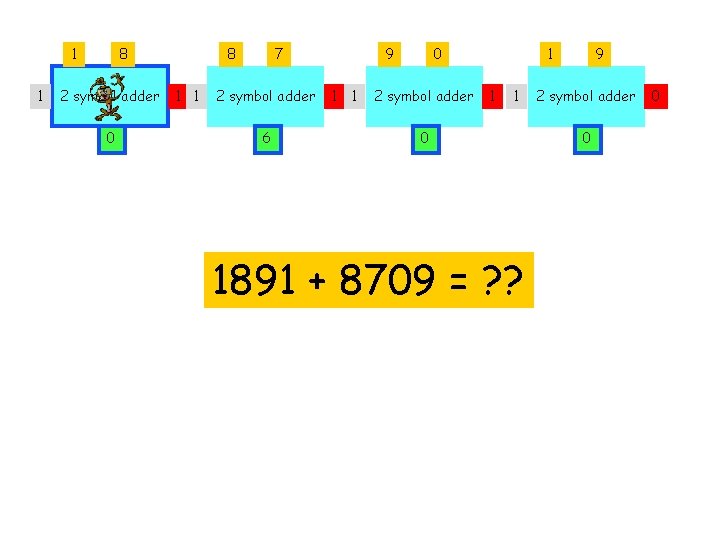
1 1 8 2 symbol adder 0 8 1 1 7 2 symbol adder 6 9 1 1 0 2 symbol adder 1 1 1 0 1891 + 8709 = ? ? 9 2 symbol adder 0 0

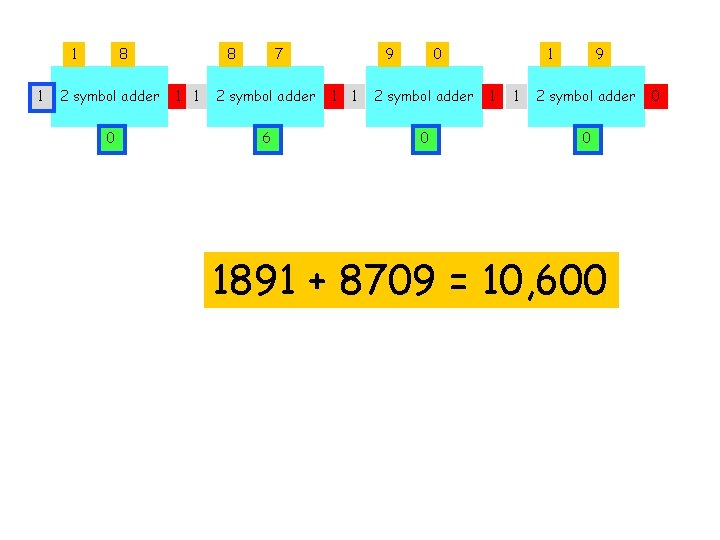
1 1 8 2 symbol adder 0 8 1 1 7 2 symbol adder 6 9 1 1 0 2 symbol adder 0 1 1 1 9 2 symbol adder 0 1891 + 8709 = 10, 600 0

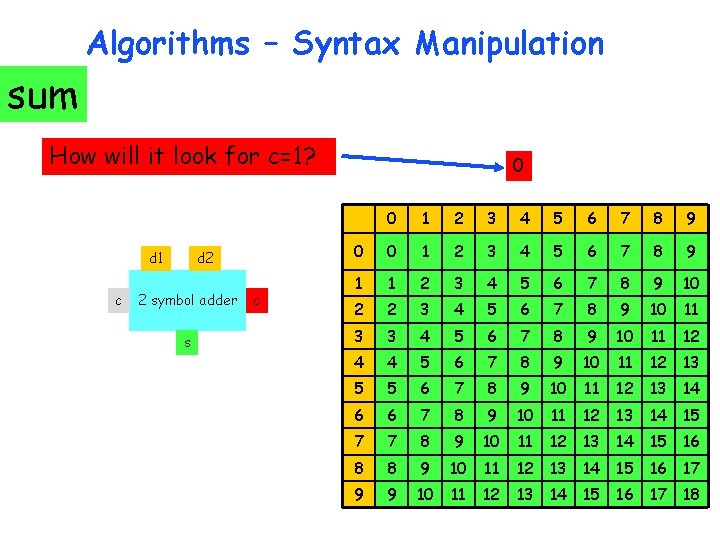
sum Algorithms – Syntax Manipulation How will it look for c=1? d 1 c d 2 2 symbol adder s c 0 0 1 2 3 4 5 6 7 8 9 10 2 2 3 4 5 6 7 8 9 10 11 3 3 4 5 6 7 8 9 10 11 12 4 4 5 6 7 8 9 10 11 12 13 5 5 6 7 8 9 10 11 12 13 14 6 6 7 8 9 10 11 12 13 14 15 7 7 8 9 10 11 12 13 14 15 16 8 8 9 10 11 12 13 14 15 16 17 9 9 10 11 12 13 14 15 16 17 18

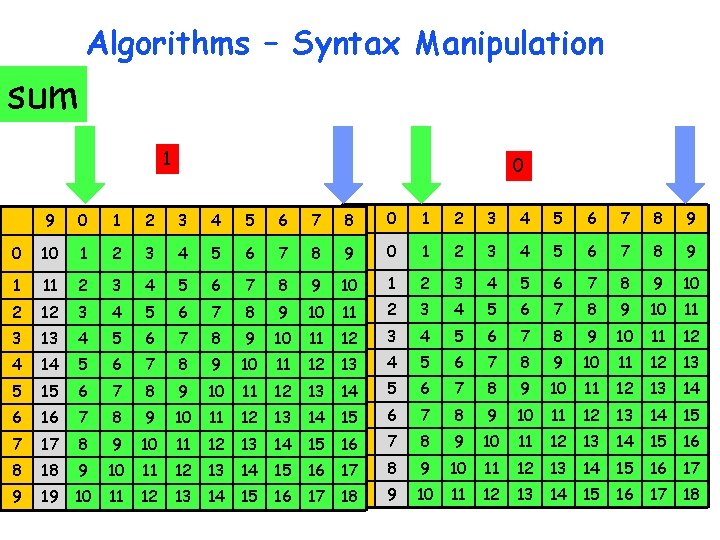
sum Algorithms – Syntax Manipulation 1 0 9 0 1 2 3 4 5 6 7 8 9 0 10 1 2 3 4 5 6 7 8 90 0 1 2 3 4 5 6 7 8 9 1 11 2 3 4 5 6 7 8 9 10 2 12 3 4 5 6 7 8 9 10 101 112 2 3 4 5 6 7 8 9 10 11 3 13 4 5 6 7 8 9 10 11 12 4 14 5 6 7 8 9 10 11 12 123 134 4 5 6 7 8 9 10 11 12 13 5 15 6 7 8 9 10 11 12 13 14 6 16 7 8 9 10 11 12 13 14 145 156 6 7 8 9 10 11 12 13 14 15 7 17 8 9 10 11 12 13 14 15 16 8 18 9 10 11 12 13 14 15 16 167 178 8 9 10 11 12 13 14 15 16 17 9 19 10 11 12 13 14 15 16 17 189 9 10 11 12 13 14 15 16 17 18

sum Algorithms – Syntax Manipulation 1 0 9 0 1 2 3 4 5 6 7 8 9 0 10 1 2 3 4 5 6 7 8 90 0 1 2 3 4 5 6 7 8 9 1 11 2 3 4 5 6 7 8 9 10 2 12 3 4 5 6 7 8 9 10 101 112 2 3 4 5 6 7 8 9 10 11 3 13 4 5 6 7 8 9 10 11 12 4 14 5 6 7 8 9 10 11 12 123 134 4 5 6 7 8 9 10 11 12 13 5 15 6 7 8 9 10 11 12 13 14 6 16 7 8 9 10 11 12 13 14 145 156 6 7 8 9 10 11 12 13 14 15 7 17 8 9 10 11 12 13 14 15 16 8 18 9 10 11 12 13 14 15 16 167 178 8 9 10 11 12 13 14 15 16 17 9 19 10 11 12 13 14 15 16 17 189 9 10 11 12 13 14 15 16 17 18

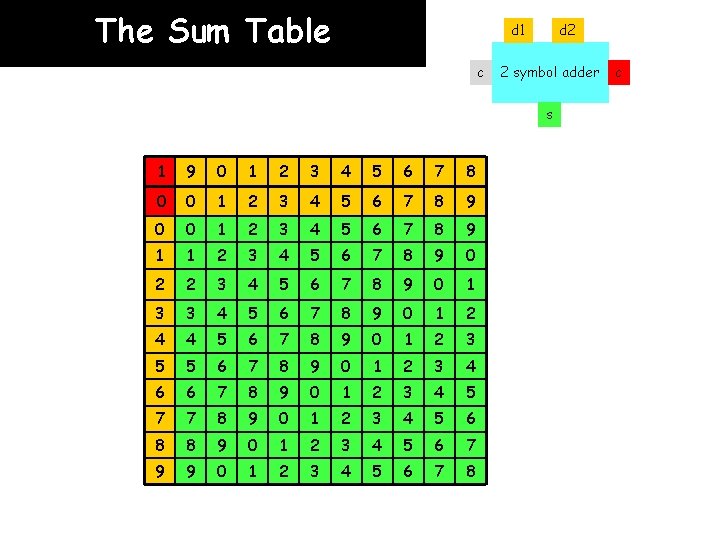
The Sum Table d 1 c d 2 2 symbol adder s 1 9 0 1 2 3 4 5 6 7 8 0 0 1 2 3 4 5 6 7 8 9 1 1 2 3 4 5 6 7 8 9 0 2 2 3 4 5 6 7 8 9 0 1 3 3 4 5 6 7 8 9 0 1 2 4 4 5 6 7 8 9 0 1 2 3 5 5 6 7 8 9 0 1 2 3 4 6 6 7 8 9 0 1 2 3 4 5 7 7 8 9 0 1 2 3 4 5 6 8 8 9 0 1 2 3 4 5 6 7 9 9 0 1 2 3 4 5 6 7 8 c

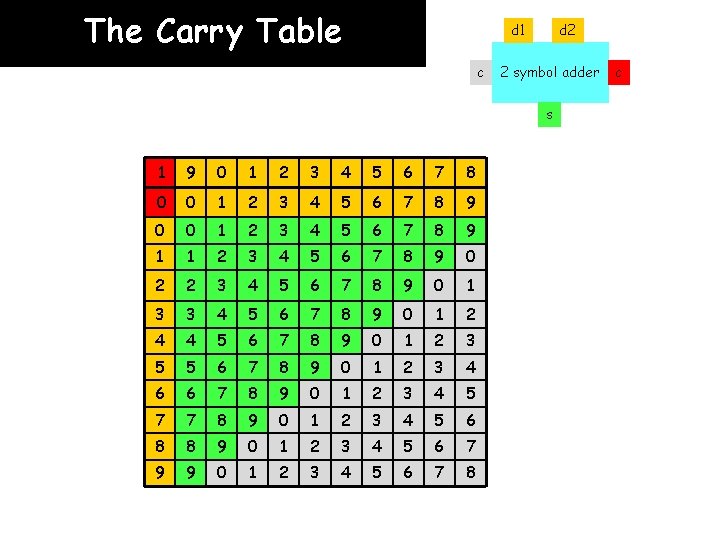
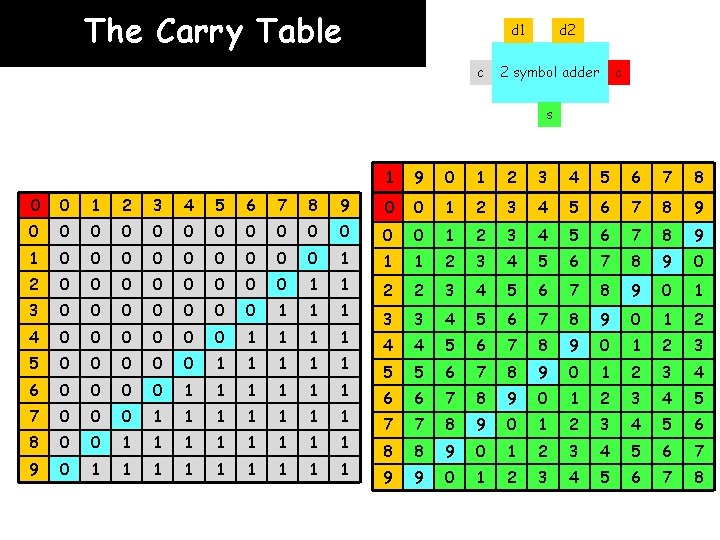
The Carry Table d 1 c d 2 2 symbol adder s 1 9 0 1 2 3 4 5 6 7 8 0 0 1 2 3 4 5 6 7 8 9 1 1 2 3 4 5 6 7 8 9 0 2 2 3 4 5 6 7 8 9 0 1 3 3 4 5 6 7 8 9 0 1 2 4 4 5 6 7 8 9 0 1 2 3 5 5 6 7 8 9 0 1 2 3 4 6 6 7 8 9 0 1 2 3 4 5 7 7 8 9 0 1 2 3 4 5 6 8 8 9 0 1 2 3 4 5 6 7 9 9 0 1 2 3 4 5 6 7 8 c

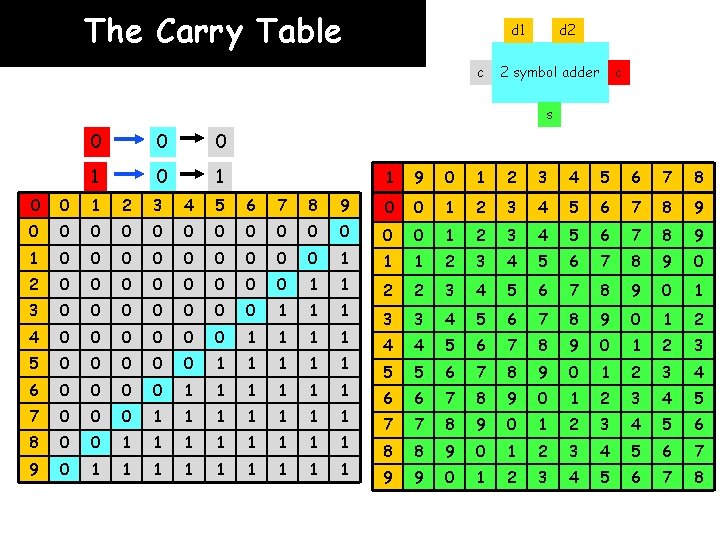
The Carry Table d 1 c d 2 2 symbol adder c s 1 9 0 1 2 3 4 5 6 7 8 0 0 1 2 3 4 5 6 7 8 9 0 0 0 0 1 2 3 4 5 6 7 8 9 1 0 0 0 0 0 1 1 1 2 3 4 5 6 7 8 9 0 2 0 0 0 0 1 1 3 0 0 0 0 1 1 1 2 2 3 4 5 6 7 8 9 0 1 4 0 0 0 1 1 3 3 4 5 6 7 8 9 0 1 2 5 0 0 0 1 1 1 4 4 5 6 7 8 9 0 1 2 3 6 0 0 1 1 1 5 5 6 7 8 9 0 1 2 3 4 7 0 0 0 1 1 1 1 6 6 7 8 9 0 1 2 3 4 5 8 0 0 1 1 1 1 7 7 8 9 0 1 2 3 4 5 6 9 0 1 1 1 1 1 8 8 9 0 1 2 3 4 5 6 7 9 9 0 1 2 3 4 5 6 7 8

The Carry Table d 1 c d 2 2 symbol adder c s 0 0 0 1 1 9 0 1 2 3 4 5 6 7 8 0 0 1 2 3 4 5 6 7 8 9 0 0 0 0 1 2 3 4 5 6 7 8 9 1 0 0 0 0 0 1 1 1 2 3 4 5 6 7 8 9 0 2 0 0 0 0 1 1 3 0 0 0 0 1 1 1 2 2 3 4 5 6 7 8 9 0 1 4 0 0 0 1 1 3 3 4 5 6 7 8 9 0 1 2 5 0 0 0 1 1 1 4 4 5 6 7 8 9 0 1 2 3 6 0 0 1 1 1 5 5 6 7 8 9 0 1 2 3 4 7 0 0 0 1 1 1 1 6 6 7 8 9 0 1 2 3 4 5 8 0 0 1 1 1 1 7 7 8 9 0 1 2 3 4 5 6 9 0 1 1 1 1 1 8 8 9 0 1 2 3 4 5 6 7 9 9 0 1 2 3 4 5 6 7 8

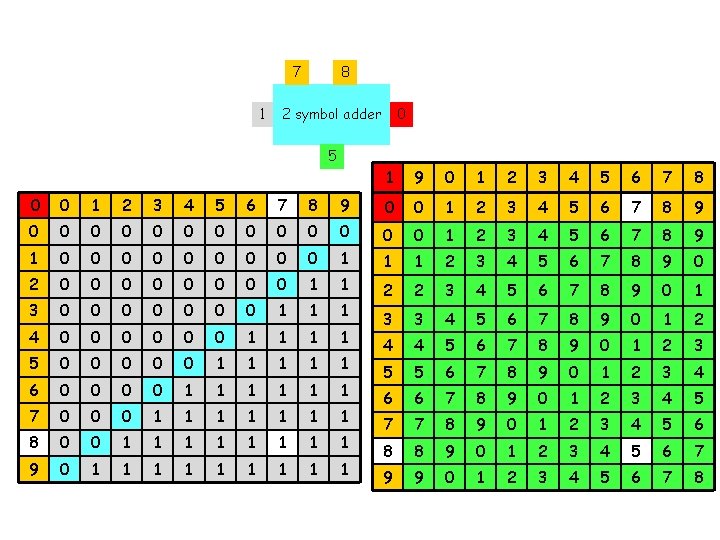
7 c 8 0 2 symbol adder s 1 9 0 1 2 3 4 5 6 7 8 0 0 1 2 3 4 5 6 7 8 9 0 0 0 0 1 2 3 4 5 6 7 8 9 1 0 0 0 0 0 1 1 1 2 3 4 5 6 7 8 9 0 2 0 0 0 0 1 1 3 0 0 0 0 1 1 1 2 2 3 4 5 6 7 8 9 0 1 4 0 0 0 1 1 3 3 4 5 6 7 8 9 0 1 2 5 0 0 0 1 1 1 4 4 5 6 7 8 9 0 1 2 3 6 0 0 1 1 1 5 5 6 7 8 9 0 1 2 3 4 7 0 0 0 1 1 1 1 6 6 7 8 9 0 1 2 3 4 5 8 0 0 1 1 1 1 7 7 8 9 0 1 2 3 4 5 6 9 0 1 1 1 1 1 8 8 9 0 1 2 3 4 5 6 7 9 9 0 1 2 3 4 5 6 7 8

7 1 8 0 2 symbol adder 5 1 9 0 1 2 3 4 5 6 7 8 0 0 1 2 3 4 5 6 7 8 9 0 0 0 0 1 2 3 4 5 6 7 8 9 1 0 0 0 0 0 1 1 1 2 3 4 5 6 7 8 9 0 2 0 0 0 0 1 1 3 0 0 0 0 1 1 1 2 2 3 4 5 6 7 8 9 0 1 4 0 0 0 1 1 3 3 4 5 6 7 8 9 0 1 2 5 0 0 0 1 1 1 4 4 5 6 7 8 9 0 1 2 3 6 0 0 1 1 1 5 5 6 7 8 9 0 1 2 3 4 7 0 0 0 1 1 1 1 6 6 7 8 9 0 1 2 3 4 5 8 0 0 1 1 1 1 7 7 8 9 0 1 2 3 4 5 6 9 0 1 1 1 1 1 8 8 9 0 1 2 3 4 5 6 7 9 9 0 1 2 3 4 5 6 7 8

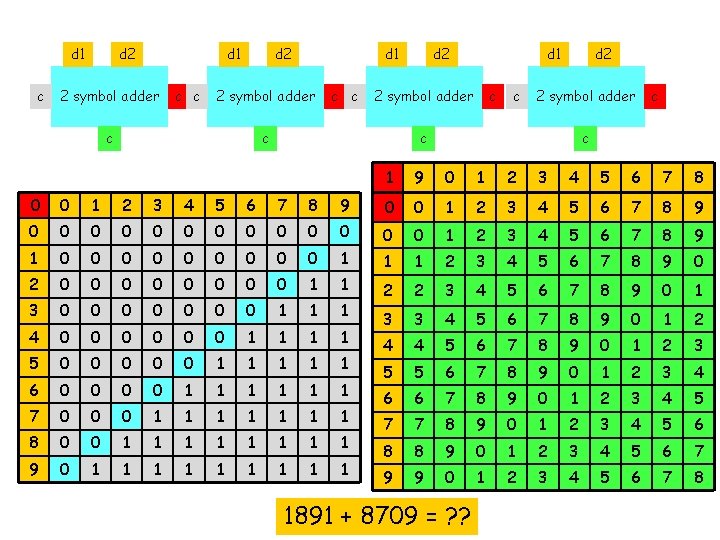
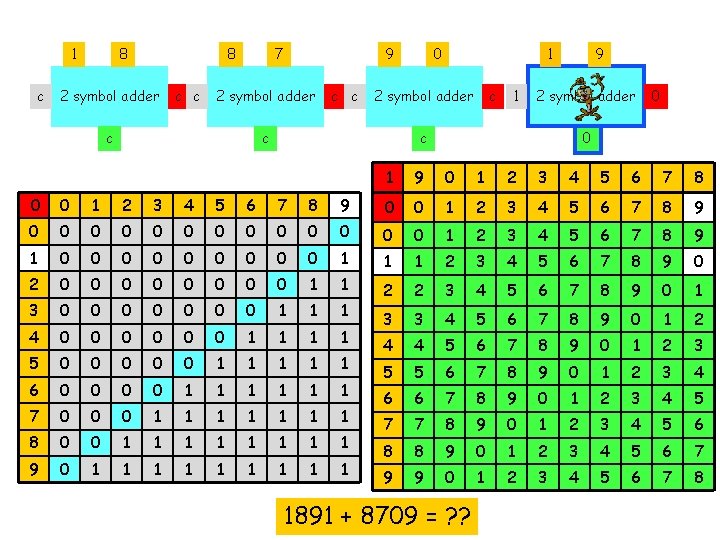
d 1 c d 2 d 1 2 symbol adder c c c d 2 2 symbol adder c c c 1 9 0 1 2 3 4 5 6 7 8 0 0 1 2 3 4 5 6 7 8 9 0 0 0 0 1 2 3 4 5 6 7 8 9 1 0 0 0 0 0 1 1 1 2 3 4 5 6 7 8 9 0 2 0 0 0 0 1 1 3 0 0 0 0 1 1 1 2 2 3 4 5 6 7 8 9 0 1 4 0 0 0 1 1 3 3 4 5 6 7 8 9 0 1 2 5 0 0 0 1 1 1 4 4 5 6 7 8 9 0 1 2 3 6 0 0 1 1 1 5 5 6 7 8 9 0 1 2 3 4 7 0 0 0 1 1 1 1 6 6 7 8 9 0 1 2 3 4 5 8 0 0 1 1 1 1 7 7 8 9 0 1 2 3 4 5 6 9 0 1 1 1 1 1 8 8 9 0 1 2 3 4 5 6 7 9 9 0 1 2 3 4 5 6 7 8 1891 + 8709 = ? ?

1 c d 2 8 2 symbol adder c c d 2 9 2 symbol adder c c c d 2 1 2 symbol adder c c c d 2 2 symbol adder c 0 c 1 9 0 1 2 3 4 5 6 7 8 0 0 1 2 3 4 5 6 7 8 9 0 0 0 0 1 2 3 4 5 6 7 8 9 1 0 0 0 0 0 1 1 1 2 3 4 5 6 7 8 9 0 2 0 0 0 0 1 1 3 0 0 0 0 1 1 1 2 2 3 4 5 6 7 8 9 0 1 4 0 0 0 1 1 3 3 4 5 6 7 8 9 0 1 2 5 0 0 0 1 1 1 4 4 5 6 7 8 9 0 1 2 3 6 0 0 1 1 1 5 5 6 7 8 9 0 1 2 3 4 7 0 0 0 1 1 1 1 6 6 7 8 9 0 1 2 3 4 5 8 0 0 1 1 1 1 7 7 8 9 0 1 2 3 4 5 6 9 0 1 1 1 1 1 8 8 9 0 1 2 3 4 5 6 7 9 9 0 1 2 3 4 5 6 7 8 1891 + 8709 = ? ?

1 c 8 8 2 symbol adder c c 7 9 2 symbol adder c c c 0 1 2 symbol adder c c c 9 2 symbol adder c 0 c 1 9 0 1 2 3 4 5 6 7 8 0 0 1 2 3 4 5 6 7 8 9 0 0 0 0 1 2 3 4 5 6 7 8 9 1 0 0 0 0 0 1 1 1 2 3 4 5 6 7 8 9 0 2 0 0 0 0 1 1 3 0 0 0 0 1 1 1 2 2 3 4 5 6 7 8 9 0 1 4 0 0 0 1 1 3 3 4 5 6 7 8 9 0 1 2 5 0 0 0 1 1 1 4 4 5 6 7 8 9 0 1 2 3 6 0 0 1 1 1 5 5 6 7 8 9 0 1 2 3 4 7 0 0 0 1 1 1 1 6 6 7 8 9 0 1 2 3 4 5 8 0 0 1 1 1 1 7 7 8 9 0 1 2 3 4 5 6 9 0 1 1 1 1 1 8 8 9 0 1 2 3 4 5 6 7 9 9 0 1 2 3 4 5 6 7 8 1891 + 8709 = ? ?

1 c 8 8 2 symbol adder c c 7 9 2 symbol adder c c c 0 1 2 symbol adder c c 1 9 2 symbol adder c 0 0 1 9 0 1 2 3 4 5 6 7 8 0 0 1 2 3 4 5 6 7 8 9 0 0 0 0 1 2 3 4 5 6 7 8 9 1 0 0 0 0 0 1 1 1 2 3 4 5 6 7 8 9 0 2 0 0 0 0 1 1 3 0 0 0 0 1 1 1 2 2 3 4 5 6 7 8 9 0 1 4 0 0 0 1 1 3 3 4 5 6 7 8 9 0 1 2 5 0 0 0 1 1 1 4 4 5 6 7 8 9 0 1 2 3 6 0 0 1 1 1 5 5 6 7 8 9 0 1 2 3 4 7 0 0 0 1 1 1 1 6 6 7 8 9 0 1 2 3 4 5 8 0 0 1 1 1 1 7 7 8 9 0 1 2 3 4 5 6 9 0 1 1 1 1 1 8 8 9 0 1 2 3 4 5 6 7 9 9 0 1 2 3 4 5 6 7 8 1891 + 8709 = ? ?

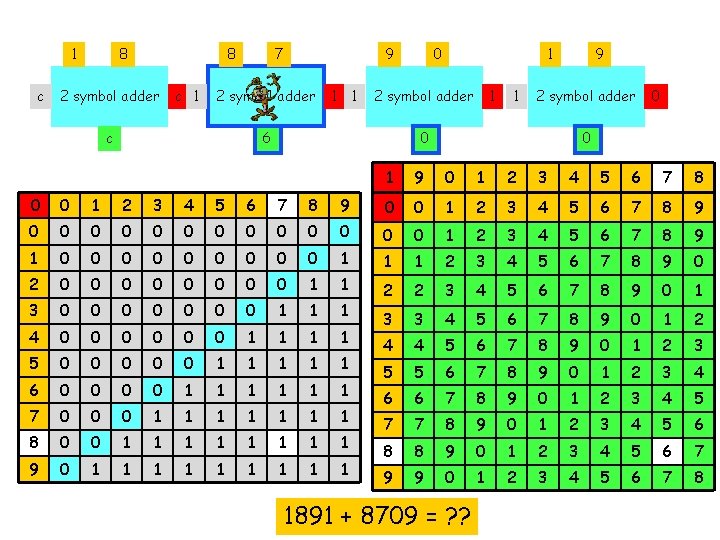
1 c 8 8 2 symbol adder c c 7 9 2 symbol adder c c 1 0 1 2 symbol adder c 1 1 9 2 symbol adder 0 0 0 1 9 0 1 2 3 4 5 6 7 8 0 0 1 2 3 4 5 6 7 8 9 0 0 0 0 1 2 3 4 5 6 7 8 9 1 0 0 0 0 0 1 1 1 2 3 4 5 6 7 8 9 0 2 0 0 0 0 1 1 3 0 0 0 0 1 1 1 2 2 3 4 5 6 7 8 9 0 1 4 0 0 0 1 1 3 3 4 5 6 7 8 9 0 1 2 5 0 0 0 1 1 1 4 4 5 6 7 8 9 0 1 2 3 6 0 0 1 1 1 5 5 6 7 8 9 0 1 2 3 4 7 0 0 0 1 1 1 1 6 6 7 8 9 0 1 2 3 4 5 8 0 0 1 1 1 1 7 7 8 9 0 1 2 3 4 5 6 9 0 1 1 1 1 1 8 8 9 0 1 2 3 4 5 6 7 9 9 0 1 2 3 4 5 6 7 8 1891 + 8709 = ? ?

1 c 8 8 2 symbol adder c 1 7 9 2 symbol adder c 1 1 0 1 2 symbol adder 6 1 1 9 2 symbol adder 0 0 0 1 9 0 1 2 3 4 5 6 7 8 0 0 1 2 3 4 5 6 7 8 9 0 0 0 0 1 2 3 4 5 6 7 8 9 1 0 0 0 0 0 1 1 1 2 3 4 5 6 7 8 9 0 2 0 0 0 0 1 1 3 0 0 0 0 1 1 1 2 2 3 4 5 6 7 8 9 0 1 4 0 0 0 1 1 3 3 4 5 6 7 8 9 0 1 2 5 0 0 0 1 1 1 4 4 5 6 7 8 9 0 1 2 3 6 0 0 1 1 1 5 5 6 7 8 9 0 1 2 3 4 7 0 0 0 1 1 1 1 6 6 7 8 9 0 1 2 3 4 5 8 0 0 1 1 1 1 7 7 8 9 0 1 2 3 4 5 6 9 0 1 1 1 1 1 8 8 9 0 1 2 3 4 5 6 7 9 9 0 1 2 3 4 5 6 7 8 1891 + 8709 = ? ?

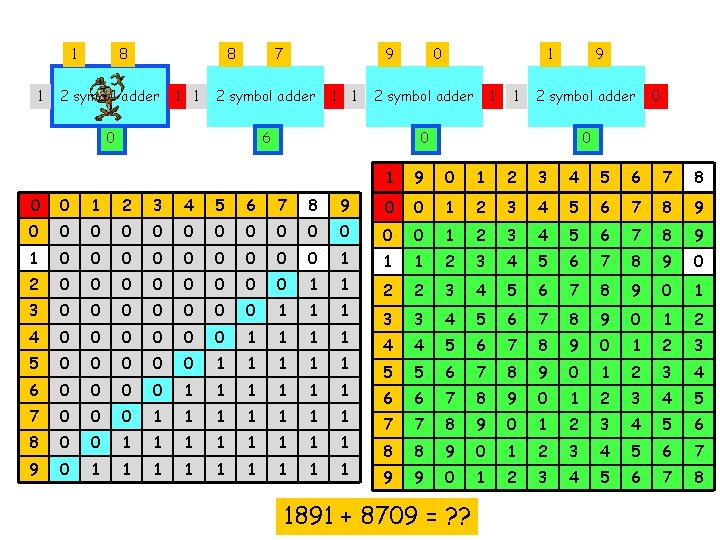
1 1 8 8 2 symbol adder 1 1 7 9 2 symbol adder 0 1 1 0 1 2 symbol adder 6 1 1 9 2 symbol adder 0 0 0 1 9 0 1 2 3 4 5 6 7 8 0 0 1 2 3 4 5 6 7 8 9 0 0 0 0 1 2 3 4 5 6 7 8 9 1 0 0 0 0 0 1 1 1 2 3 4 5 6 7 8 9 0 2 0 0 0 0 1 1 3 0 0 0 0 1 1 1 2 2 3 4 5 6 7 8 9 0 1 4 0 0 0 1 1 3 3 4 5 6 7 8 9 0 1 2 5 0 0 0 1 1 1 4 4 5 6 7 8 9 0 1 2 3 6 0 0 1 1 1 5 5 6 7 8 9 0 1 2 3 4 7 0 0 0 1 1 1 1 6 6 7 8 9 0 1 2 3 4 5 8 0 0 1 1 1 1 7 7 8 9 0 1 2 3 4 5 6 9 0 1 1 1 1 1 8 8 9 0 1 2 3 4 5 6 7 9 9 0 1 2 3 4 5 6 7 8 1891 + 8709 = ? ?

1 1 8 8 2 symbol adder 1 1 7 9 2 symbol adder 0 1 1 0 1 2 symbol adder 6 1 1 9 2 symbol adder 0 0 0 1 9 0 1 2 3 4 5 6 7 8 0 0 1 2 3 4 5 6 7 8 9 0 0 0 0 1 2 3 4 5 6 7 8 9 1 0 0 0 0 0 1 1 1 2 3 4 5 6 7 8 9 0 2 0 0 0 0 1 1 3 0 0 0 0 1 1 1 2 2 3 4 5 6 7 8 9 0 1 4 0 0 0 1 1 3 3 4 5 6 7 8 9 0 1 2 5 0 0 0 1 1 1 4 4 5 6 7 8 9 0 1 2 3 6 0 0 1 1 1 5 5 6 7 8 9 0 1 2 3 4 7 0 0 0 1 1 1 1 6 6 7 8 9 0 1 2 3 4 5 8 0 0 1 1 1 1 7 7 8 9 0 1 2 3 4 5 6 9 0 1 1 1 1 1 8 8 9 0 1 2 3 4 5 6 7 9 9 0 1 2 3 4 5 6 7 8 1891 + 8709 = 10, 600

Algorithm = a procedure for syntax manipulation Dear Algo and Fibo, we get confused with those large tables. . . can we use a smaller syntax?

The Binary

When was the binary system “invented”? (11010100111)2 (1703)10

Gottfried Leibniz 1646 -1716 Leibniz – Binary System Algorithm = a procedure for syntax manipulation

Gottfried Leibniz 1646 -1716 Algorithm = a procedure for syntax manipulation

Gottfried Leibniz 1646 -1716 Algorithm = a procedure for syntax manipulation

Gottfried Leibniz 1646 -1716 Algorithm = a procedure for syntax manipulation Use the smallest syntax possible Binary – 0 and 1

Gottfried Leibniz 1646 -1716 ? ? 8

Gottfried Leibniz 1646 -1716 Binary Addition carry

Gottfried Leibniz 1646 -1716 Binary Multiplication 3 5 6 10 5 20 Addition of shifted versions

Leibniz: No Need for Flash Cards!

Gottfried Leibniz 1646 -1716 Invented the Binary System?

Gottfried Leibniz 1646 -1716 Leibniz – Binary System Wen Wang (who flourished in about 1150 BC) is traditionally thought to have been author of the present hexagrams 63

Gottfried Leibniz 1646 -1716 Leibniz – Binary System

Arithmetic Boxes binary

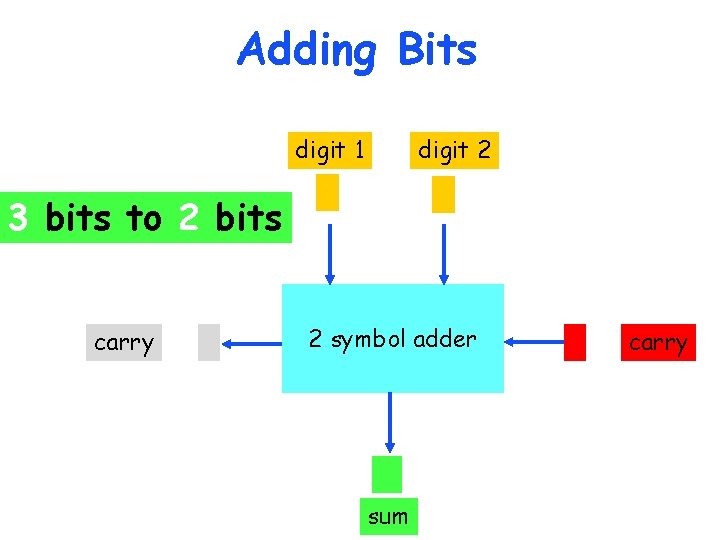
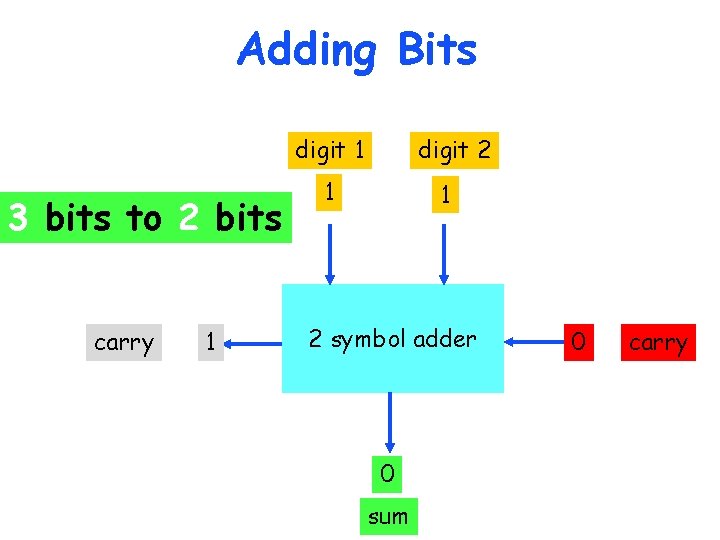
Adding Bits digit 1 digit 2 3 bits to 2 bits carry 2 symbol adder sum carry

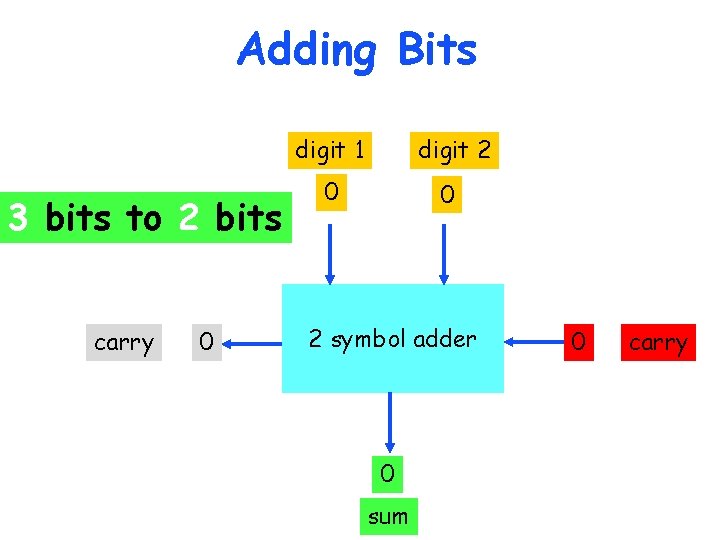
Adding Bits digit 1 3 bits to 2 bits carry 0 digit 2 0 0 2 symbol adder 0 sum 0 carry

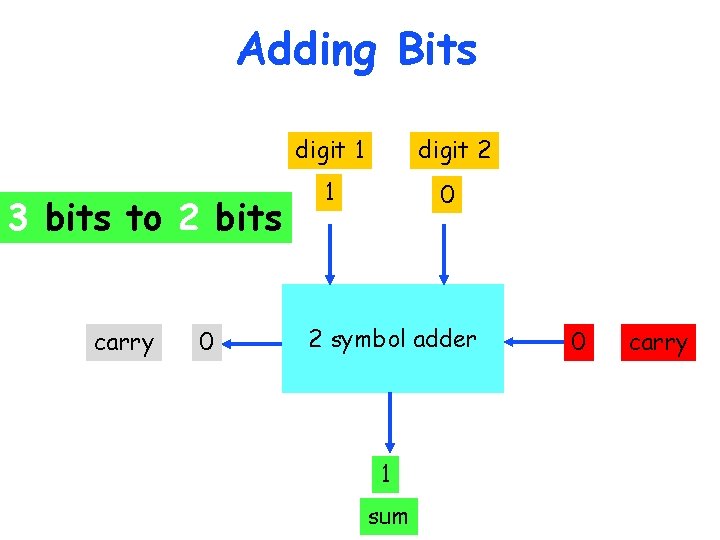
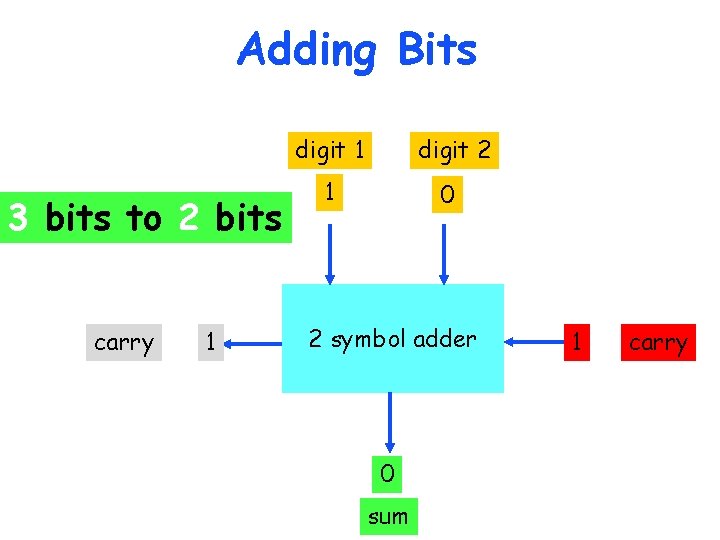
Adding Bits digit 1 3 bits to 2 bits carry 0 digit 2 1 0 2 symbol adder 1 sum 0 carry

Adding Bits digit 1 3 bits to 2 bits carry 1 digit 2 1 1 2 symbol adder 0 sum 0 carry

Adding Bits digit 1 3 bits to 2 bits carry 1 digit 2 1 0 2 symbol adder 0 sum 1 carry

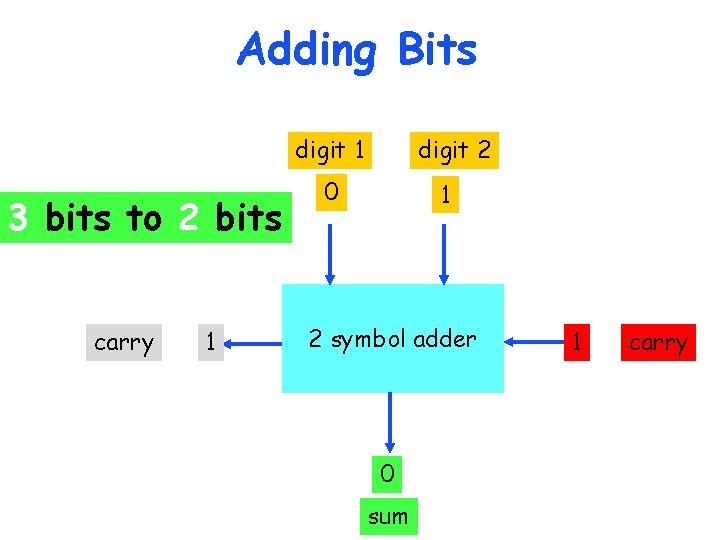
Adding Bits digit 1 3 bits to 2 bits carry 1 digit 2 0 1 2 symbol adder 0 sum 1 carry

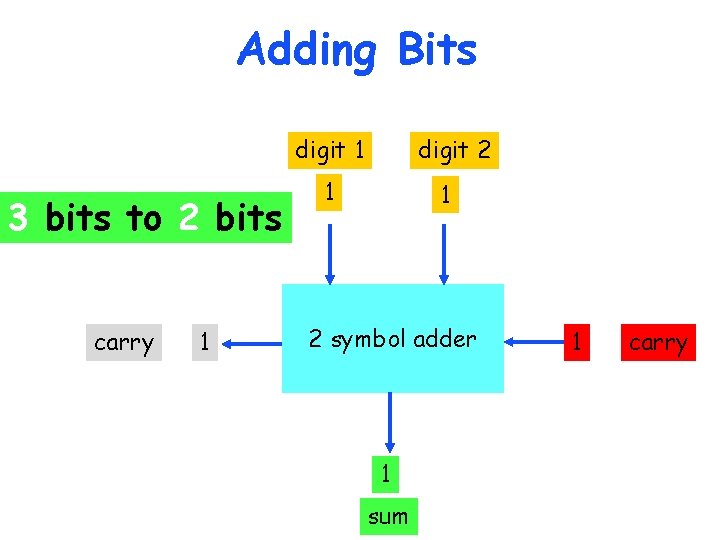
Adding Bits digit 1 3 bits to 2 bits carry 1 digit 2 1 1 2 symbol adder 1 sum 1 carry

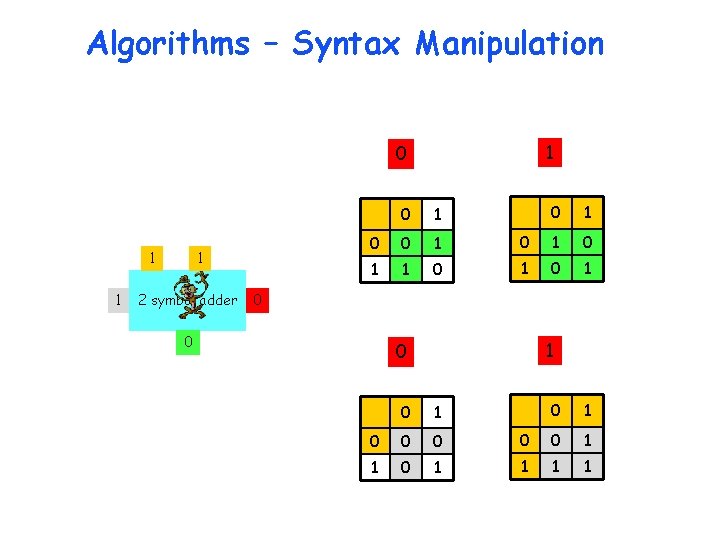
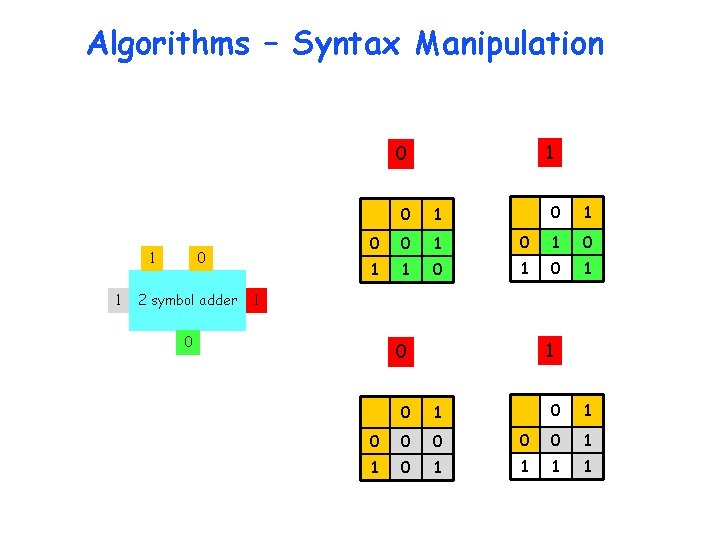
Algorithms – Syntax Manipulation 0 d 1 c d 2 2 symbol adder s c 0 1 2 3 4 5 6 7 8 9 0 0 1 2 3 4 5 6 7 8 9 1 1 2 3 4 5 6 7 8 9 2 2 3 4 5 6 7 8 9 3 3 4 5 6 7 8 9 4 4 5 6 7 8 9 5 5 6 7 8 9 6 6 7 8 9 7 7 8 9 8 8 9 9 9

Algorithms – Syntax Manipulation 0 0 1 1 1 2 1 1 0 sum d 1 c d 2 2 symbol adder c 0 1 0 0 1 1 1 0 0 1 0 1 s 1 0 carry 0 1 0 0 0 1 0 1 0 0 1 1 0 1 2 1 2 3

Algorithms – Syntax Manipulation 1 0 1 1 1 2 symbol adder 0 1 0 0 1 1 1 0 0 1 0 0 0 1 0 1 0 0 1 1

Algorithms – Syntax Manipulation 1 0 1 1 0 2 symbol adder 0 1 0 0 1 1 1 0 0 1 0 0 0 1 0 1 0 0 1 1

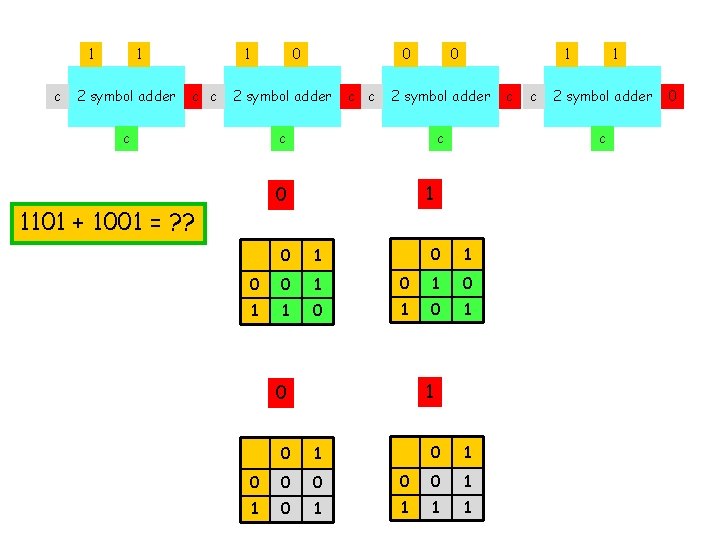
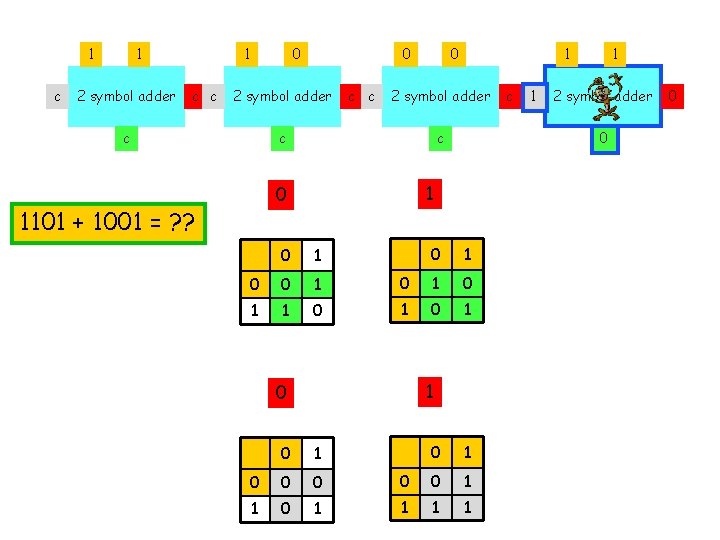
1 c 1 2 symbol adder 1 c c 0 0 2 symbol adder c c c 0 2 symbol adder c c 0 1 0 0 1 1 1 0 0 1 0 1 1 0 0 0 1 c c 1 2 symbol adder c 1 0 1101 + 1001 = ? ? 1 0 0 1 1 0

1 c 1 2 symbol adder 1 c c 0 0 2 symbol adder c c c 0 2 symbol adder c c 0 1 0 0 1 1 1 0 0 1 0 1 1 0 0 0 1 c 1 1 2 symbol adder 0 1101 + 1001 = ? ? 1 0 0 1 1 0

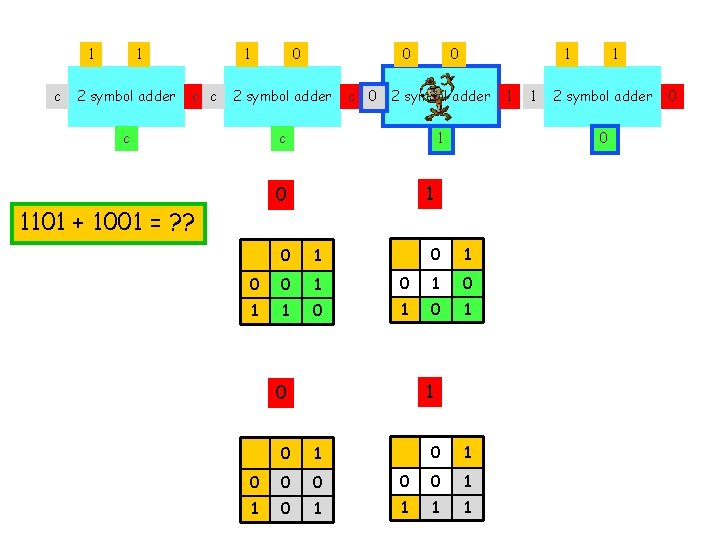
1 c 1 2 symbol adder 1 c c 0 0 2 symbol adder c 1 0 0 1 1 1 0 0 1 0 1 1 0 0 0 1 1 1 1 2 symbol adder 0 1101 + 1001 = ? ? 1 0 0 1 1 0

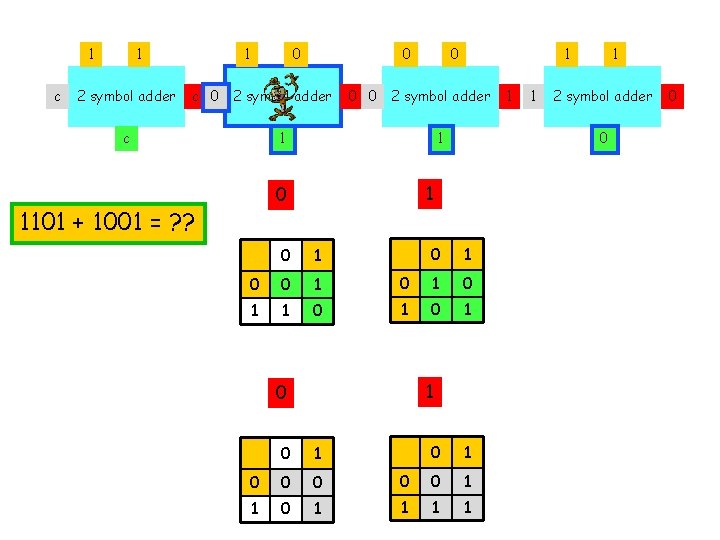
1 c 1 2 symbol adder 1 c 0 0 0 2 symbol adder 1 1 0 0 1 0 1 1 0 0 0 1 1 1 1 2 symbol adder 0 1101 + 1001 = ? ? 1 0 0 1 1 0

1 1 1 2 symbol adder 1 0 0 0 0 2 symbol adder 1 1 0 0 1 0 1 1 0 0 0 1 1 1 1 2 symbol adder 0 1101 + 1001 = ? ? 1 0 0 1 1 0

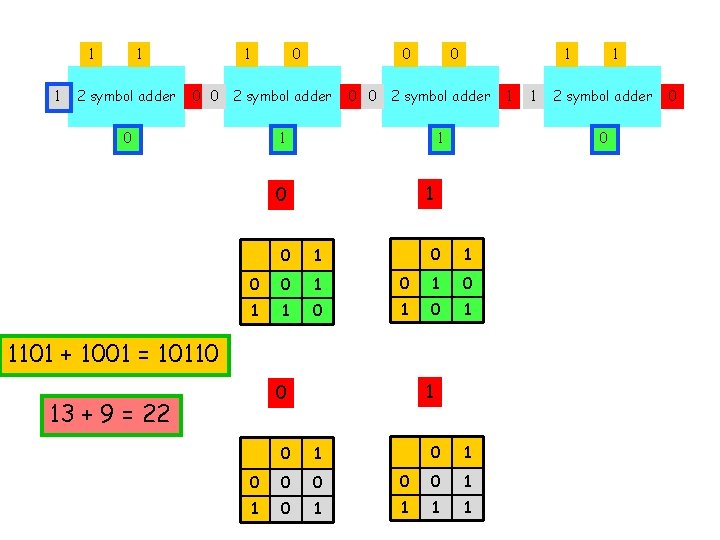
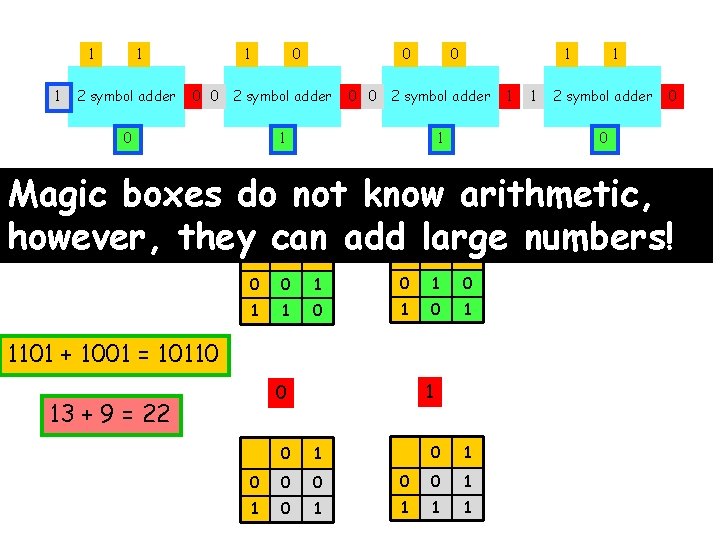
1 1 1 2 symbol adder 1 0 0 2 symbol adder 0 0 1 2 symbol adder 1 1 0 0 1 0 1 1101 + 1001 = 10110 1 0 13 + 9 = 22 0 1 0 0 0 1 1 2 symbol adder 0 1 1 0

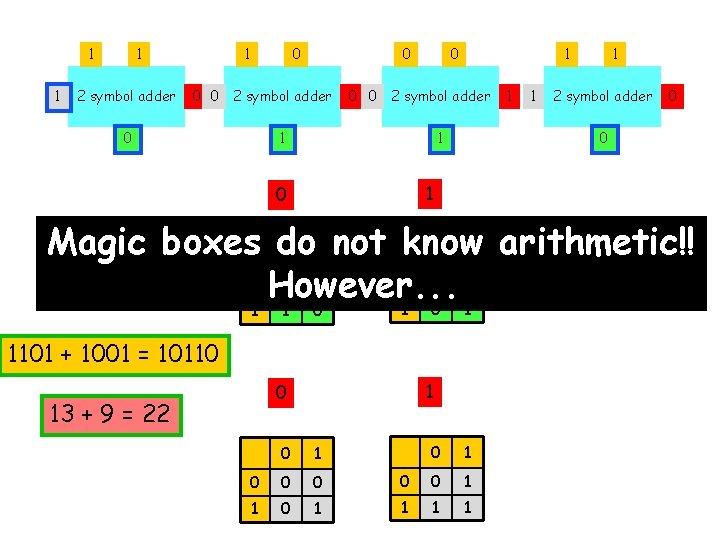
1 1 1 2 symbol adder 1 0 0 2 symbol adder 0 0 1 2 symbol adder 1 1 1 2 symbol adder 0 0 1 0 Magic boxes do arithmetic!! 0 1 not know 0 1 0 0 However. . . 0 1 1 1 0 1 1101 + 1001 = 10110 1 0 13 + 9 = 22 0 1 0 0 0 1 0 1 0 0 1 1

Arithmetic Boxes meet magic boxes

Finite Universality Magic Syntax Boxes universal set of building blocks Can construct ‘everything’ There is a finite a b m 0 0 1 1 0 a b m

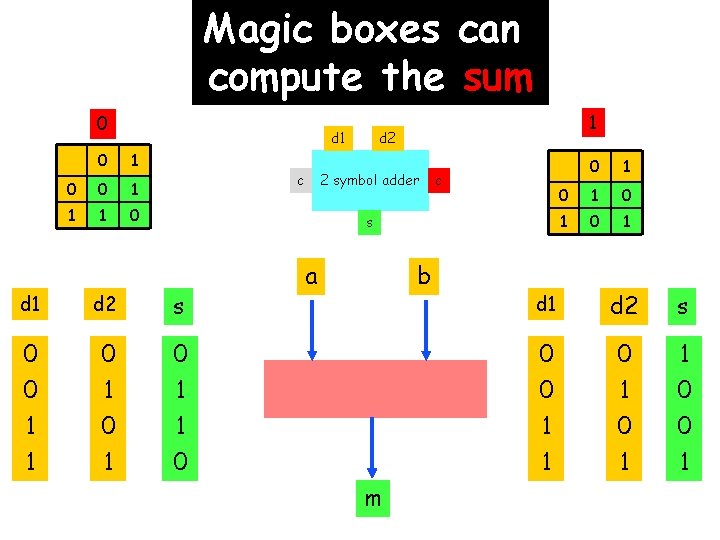
Magic boxes can compute the sum 0 d 1 0 0 1 1 1 0 1 d 2 2 symbol adder c c s d 1 d 2 s 0 0 1 1 0 1 0 1 1 0 a b m 0 1 0 1 d 1 d 2 s 0 0 1 1 0 0 1

Magic boxes can compute the carry 0 d 1 0 0 0 1 1 d 2 2 symbol adder c c s d 1 d 2 c 0 0 1 1 0 1 0 0 0 1 a b m 0 1 0 0 1 1 d 1 d 2 c 0 0 1 1 0 1 0 1 1 1

1 1 1 2 symbol adder 1 0 0 2 symbol adder 0 0 1 2 symbol adder 1 1 1 2 symbol adder 0 0 1 arithmetic, Magic boxes do 0 not know however, they can add large numbers! 0 1 0 1 0 1 1101 + 1001 = 10110 1 0 13 + 9 = 22 0 1 0 0 0 1 0 1 0 0 1 1

Gottfried Leibniz 1646 -1716 What do you see? Leibniz, Bernoulli and ? ? 0 0 0 1 0 0 0 0 1 0 1 0 0 0 1 1 0 0 1 1 0 0 0 1 Jakob Bernoulli 1654 -1705

Gottfried Leibniz 1646 -1716 What do you see? Leibniz, Bernoulli and Squares 0 1 0 0 0 1 4 9 0 0 0 16 25 36 49 0 1 0 0 1 1 0 0 0 1 Jakob Bernoulli 1654 -1705

Leibniz, Bernoulli and Squares Gottfried Leibniz 1646 -1716 Jakob Bernoulli 1654 -1705 Proof? Statement: Gray bits alternate between 0 and 1 What do you see? 0 1 Convince a friend 4 that this statement is true 9 0 0 0 1 0 0 0 0 1 - Square of even number is even 16 0 1 0 0 - Square of odd number is odd 25 0 1 1 0 0 1 36 1 0 0 In base-2, even number ends with a 0 49 with 1 1 a 10 0 0 1 odd number ends

Leibniz, Bernoulli and Squares Gottfried Leibniz 1646 -1716 Statement: The second bit of squares is always 0 What do you see? Proof? 0 1 0 0 0 1 4 9 0 0 0 16 25 36 49 0 1 0 0 1 1 0 0 0 1 Jakob Bernoulli 1654 -1705

Gottfried Leibniz 1646 -1716 Jakob Bernoulli 1654 -1705 Proof Statement: The second bit of squares is always 0 Even number: Key observation: What is the remainder if we divide a square by 4? Odd number: 0 1

Gottfried Leibniz 1646 -1716 Proof Statement: The second bit of squares is always 0 If we divide a square by 4 the remainder is either 0 or 1 0 0 0 1 4 9 0 0 0 1 0 0 The two right most bits in the binary representation 16 are the remainder if 25 we divide by 4 36 49 0 0 1 0 1 0 0 0 1 1 0 0 1 1 0 0 0 1 Jakob Bernoulli 1654 -1705

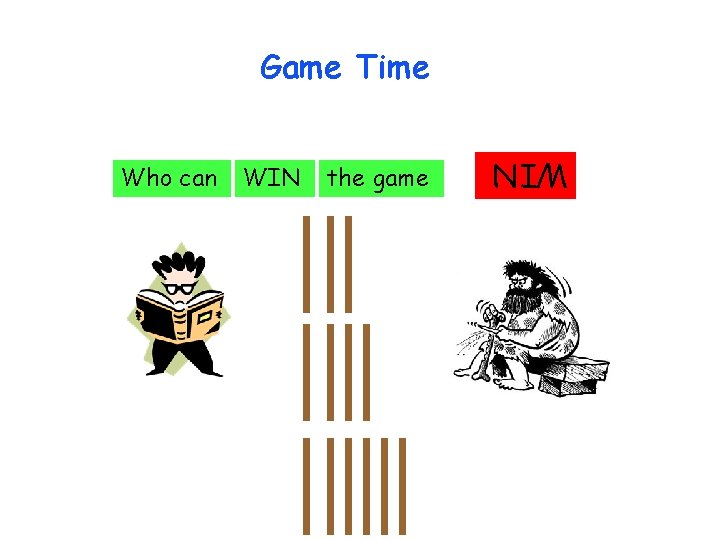
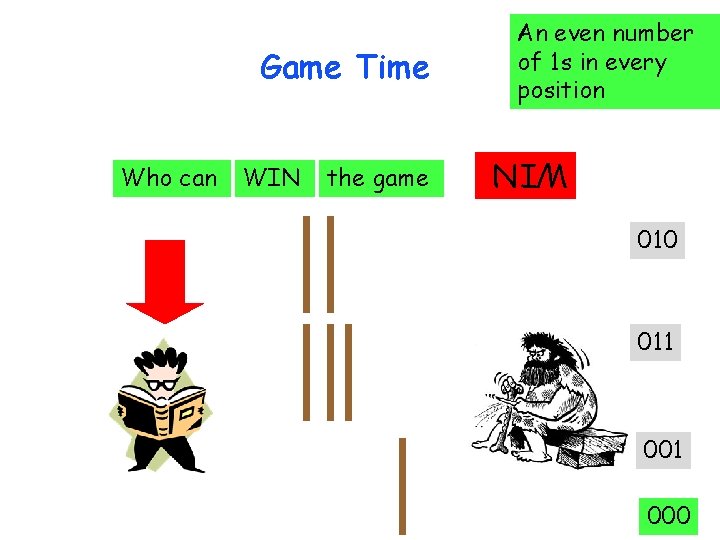
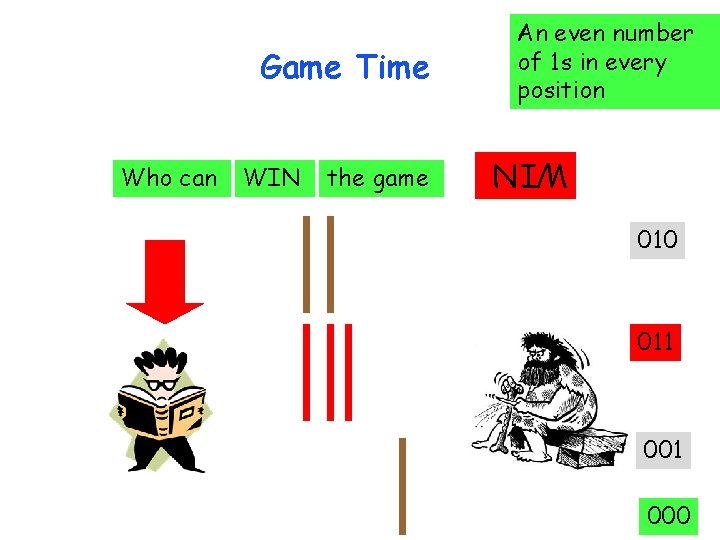
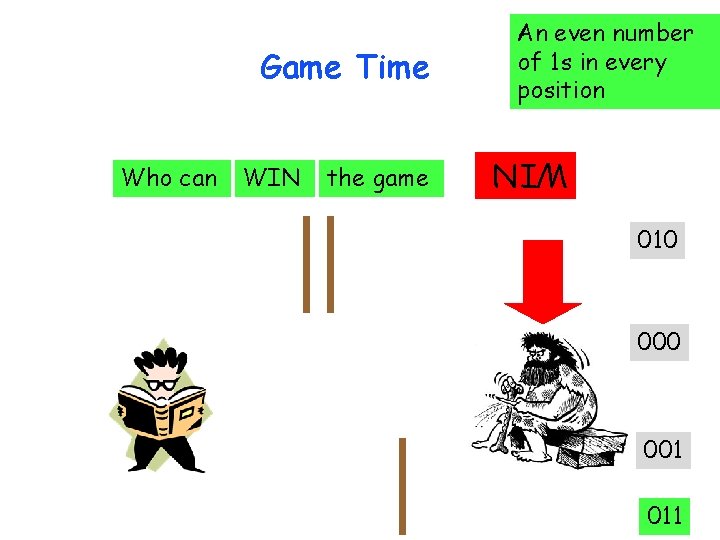
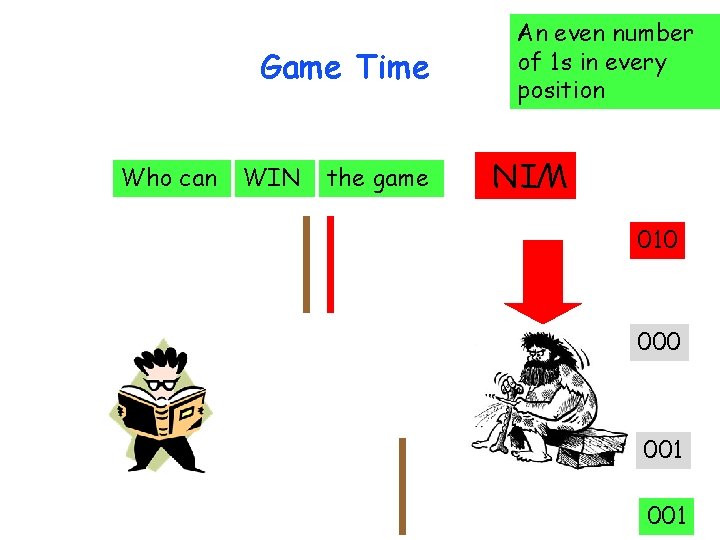
Game time

Game Time Who can VI WIN the game WIN

Game Time WIN the game WIN Who can

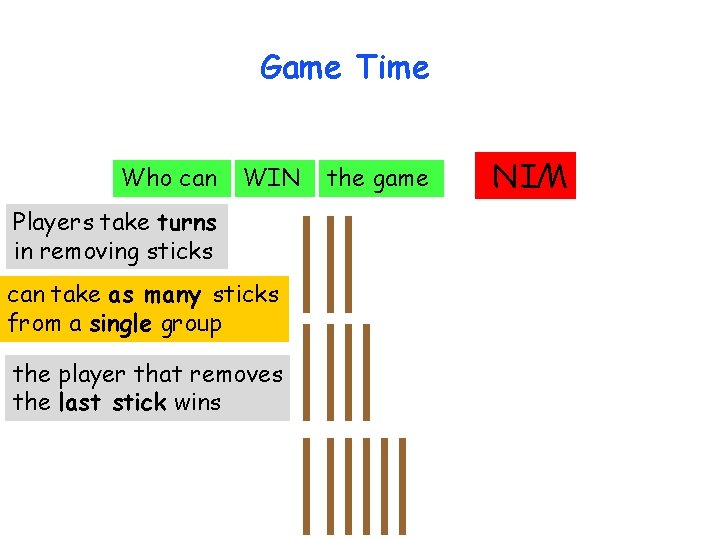
Game Time WIN Players take turns in removing sticks can take as many sticks from a single group the player that removes the last stick wins the game WIN Who can

Game Time WIN the game WIN Who can

Game Time WIN the game WIN Who can

Game Time WIN the game WIN Who can

Game Time WIN the game WIN Who can

Game Time WIN the game WIN Who can

Game Time WIN the game WIN Who can

Game Time WIN the game WIN Who can

Game Time WIN the game WIN Who can

Game Time WIN the game WIN Who can

Game Time WIN the game WIN Who can

Game Time WIN the game WIN Who can

Game Time WIN the game WIN Who can

Game Time WIN the game WIN Who can

Game Time WIN the game WIN Who can I CAN

Game Time Who can WIN the game WIN VI=110

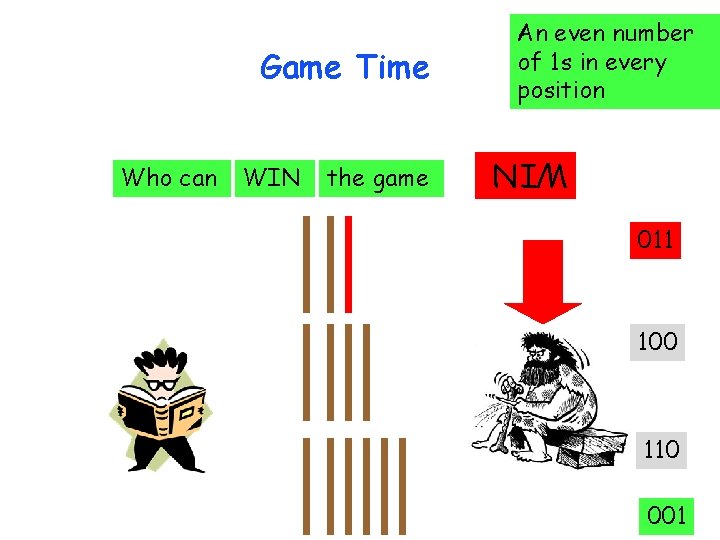
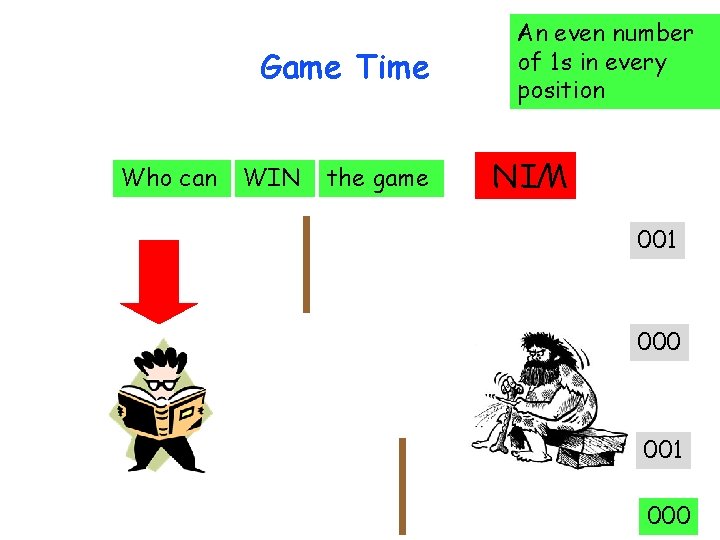
Who can WIN the game WIN Game Time An even number of 1 s in every position 011 100 110 001

Who can WIN the game WIN Game Time An even number of 1 s in every position 011 100 110 001

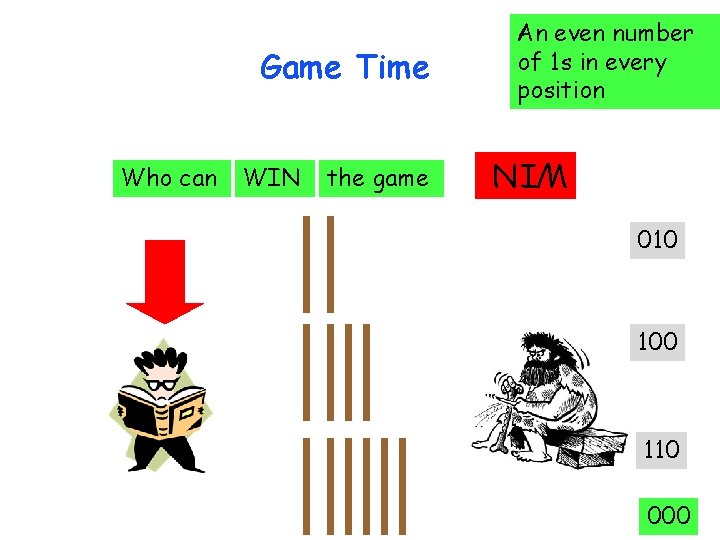
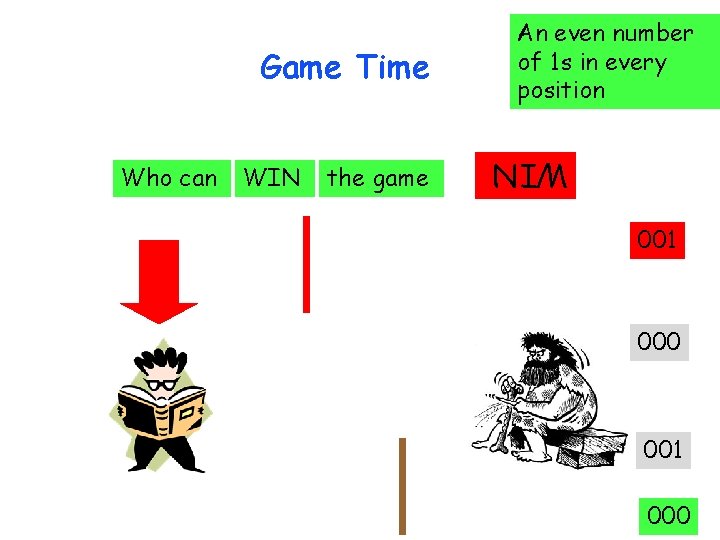
Who can WIN the game WIN Game Time An even number of 1 s in every position 010 100 110 000

Who can WIN the game WIN Game Time An even number of 1 s in every position 010 100 110 000

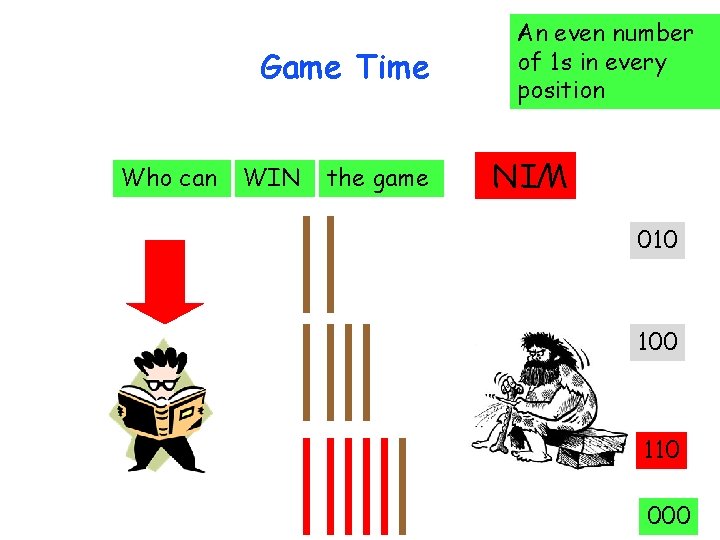
Who can WIN the game WIN Game Time An even number of 1 s in every position 010 100 001 111

Who can WIN the game WIN Game Time An even number of 1 s in every position 010 100 001 111

Who can WIN the game WIN Game Time An even number of 1 s in every position 010 011 000

Who can WIN the game WIN Game Time An even number of 1 s in every position 010 011 000

Who can WIN the game WIN Game Time An even number of 1 s in every position 010 011 000

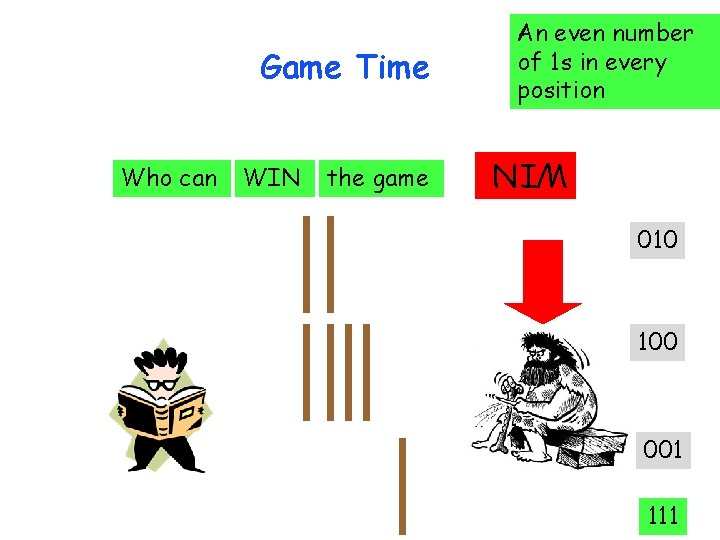
Who can WIN the game WIN Game Time An even number of 1 s in every position 010 001 011

Who can WIN the game WIN Game Time An even number of 1 s in every position 010 001 001

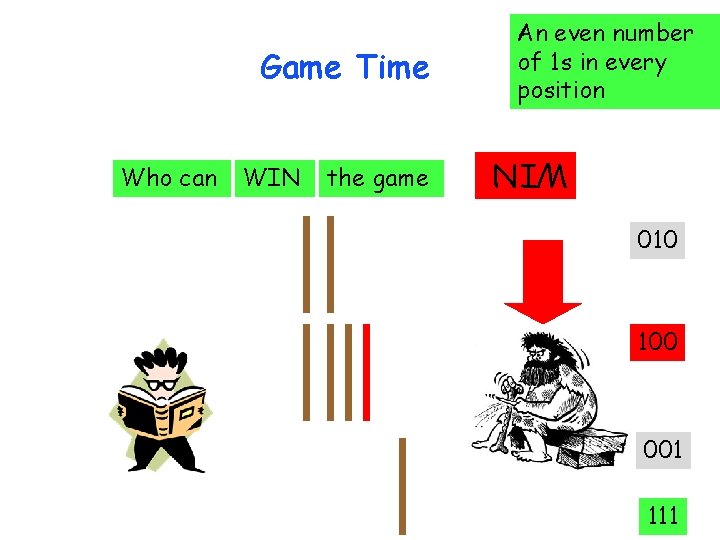
Who can WIN the game WIN Game Time An even number of 1 s in every position 001 000

Who can WIN the game WIN Game Time An even number of 1 s in every position 001 000

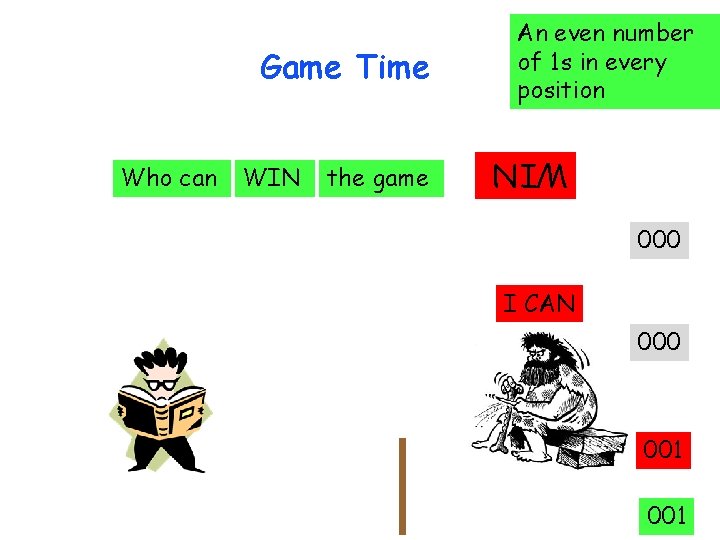
Who can WIN the game WIN Game Time An even number of 1 s in every position 000 I CAN 000 001

Who can WIN the game Winning starts with the choice of the right language WIN Game Time An even number of 1 s in every position 000 I CAN 000 000

Who can WIN the game WIN Game Time An even number of 1 s in every position 000 000