ISO 19107 Geographic information Spatial schema Pusan National

ISO 19107 Geographic information – Spatial schema Pusan National University Dept. of Computer Engineering Spatiotemporal Database Lab. Joon-Seok Kim joonseok@pnu. edu

Outline • Introduction • Schema – Geometry • • • Geometry root Geometry primitive Coordinate geometry Geometry aggregate Geometry complex – Topology • Topology root • Topology primitive • Topology complex • Summary 2

Introduction • ISO 19107 – Providing conceptual schemas for describing and manipulating the spatial characteristic – Formal language • Unified Modeling Language (UML) ISO 19103 – Vector geometry and topology up to 3 -D – Spatial operations • For use in access, query, management, processing, and data exchange of geographic information 3

4 Package Clients of ISO 19107

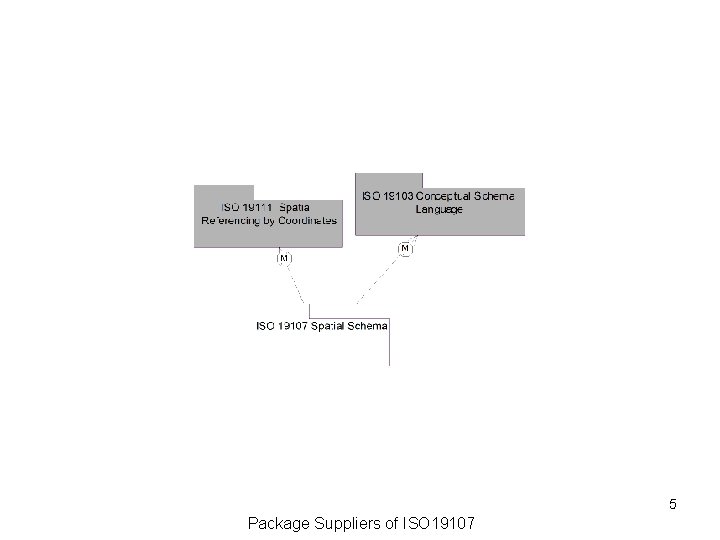
5 Package Suppliers of ISO 19107

6 Main Diagram of ISO 19107 Spatial Schema

Geometry

8 Geometry Packages

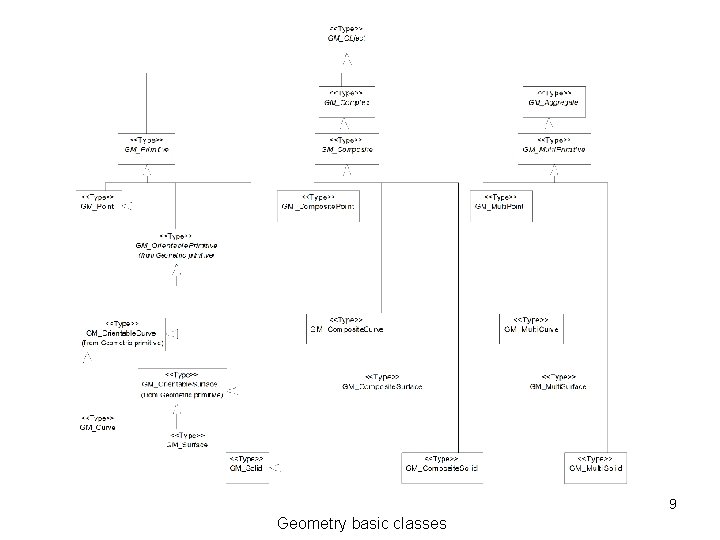
9 Geometry basic classes

Basic Concept Geometry object Point Line Rectangle … Infinite set of points Point set theory 10

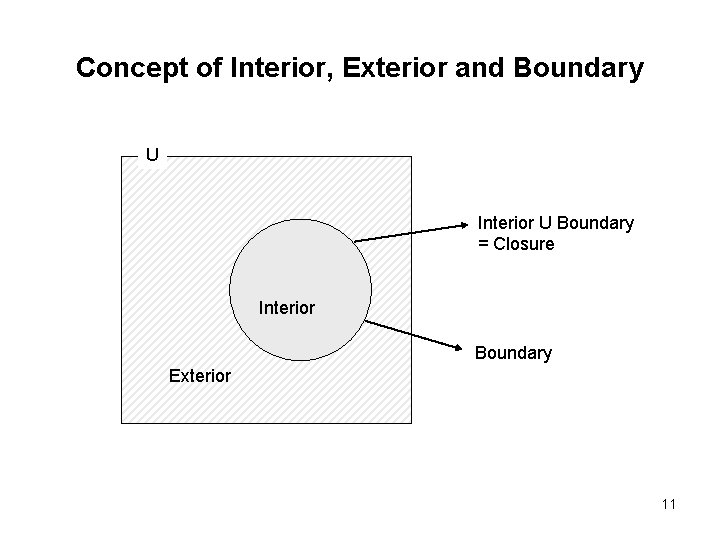
Concept of Interior, Exterior and Boundary U Interior U Boundary = Closure Interior Boundary Exterior 11

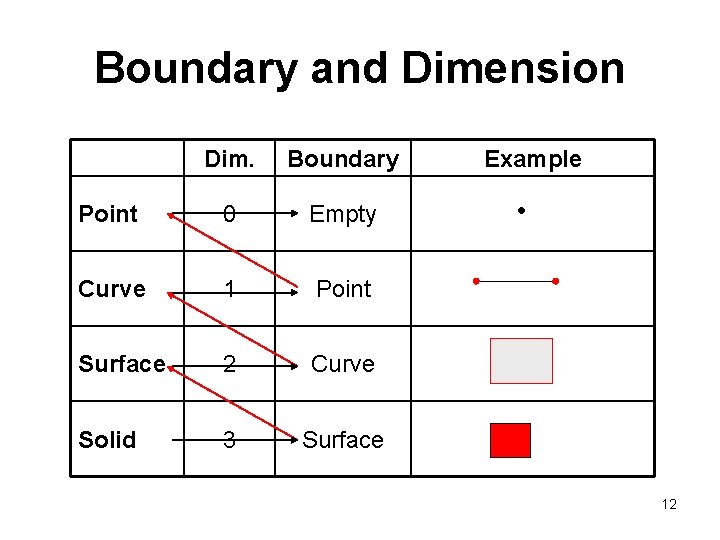
Boundary and Dimension Dim. Boundary Point 0 Empty Curve 1 Point Surface 2 Curve Solid 3 Surface Example 12

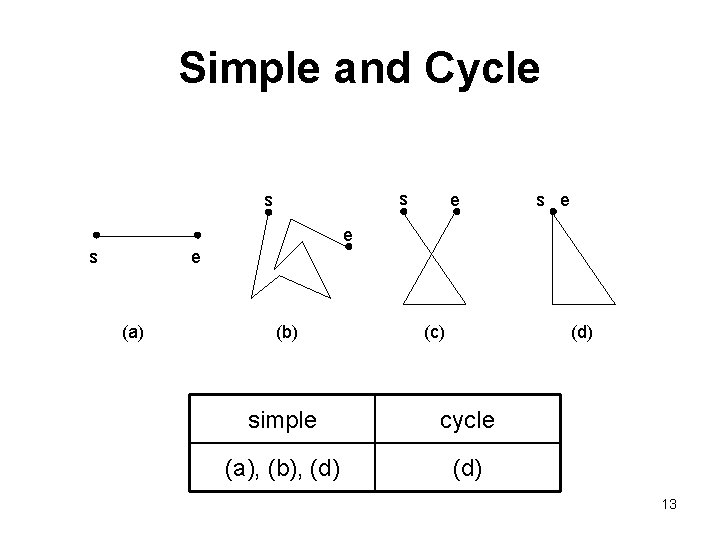
Simple and Cycle s s e e s e (a) (b) (c) (d) simple cycle (a), (b), (d) 13

14 GM_Object

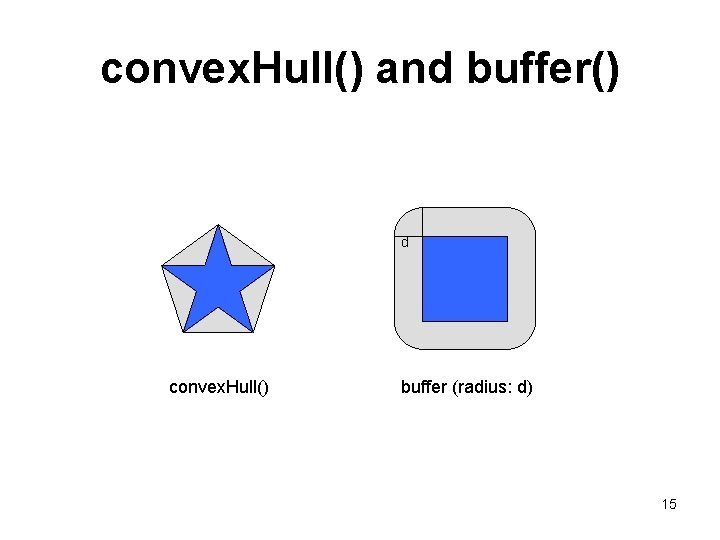
convex. Hull() and buffer() d convex. Hull() buffer (radius: d) 15

16 Geometry Boundary Data Types

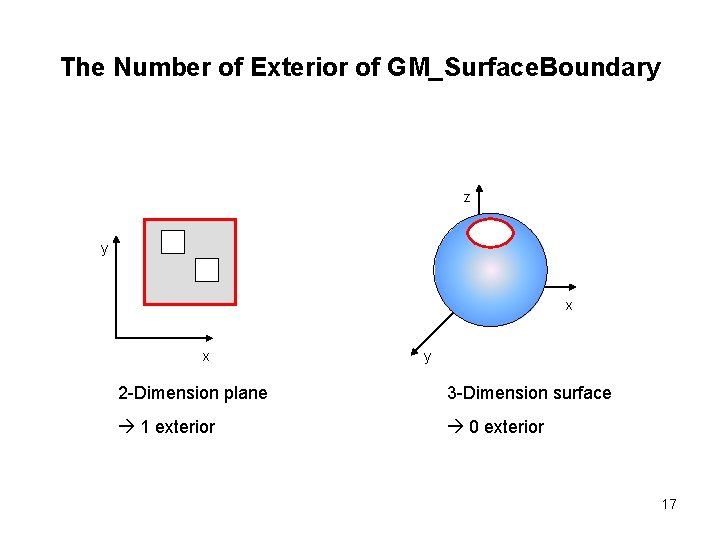
The Number of Exterior of GM_Surface. Boundary z y x x y 2 -Dimension plane 3 -Dimension surface 1 exterior 0 exterior 17

18 GM_Primitive

Geometric Primitive

20 GM_Point

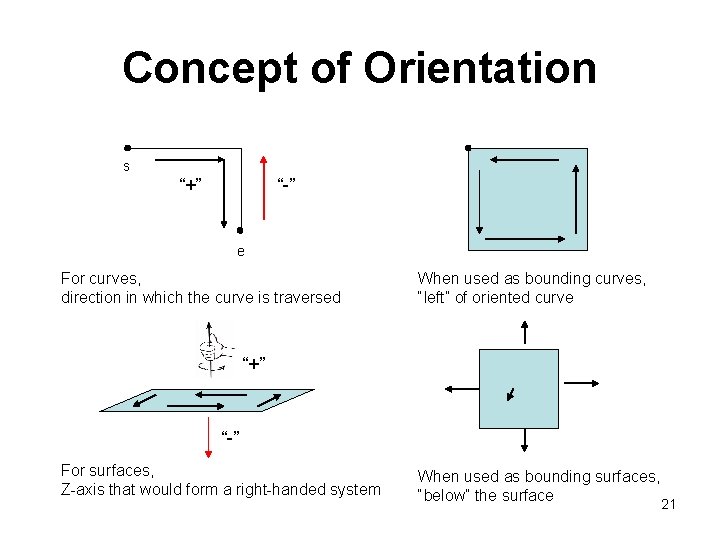
Concept of Orientation s “+” “-” e For curves, direction in which the curve is traversed When used as bounding curves, “left” of oriented curve “+” “-” For surfaces, Z-axis that would form a right-handed system When used as bounding surfaces, “below” the surface 21

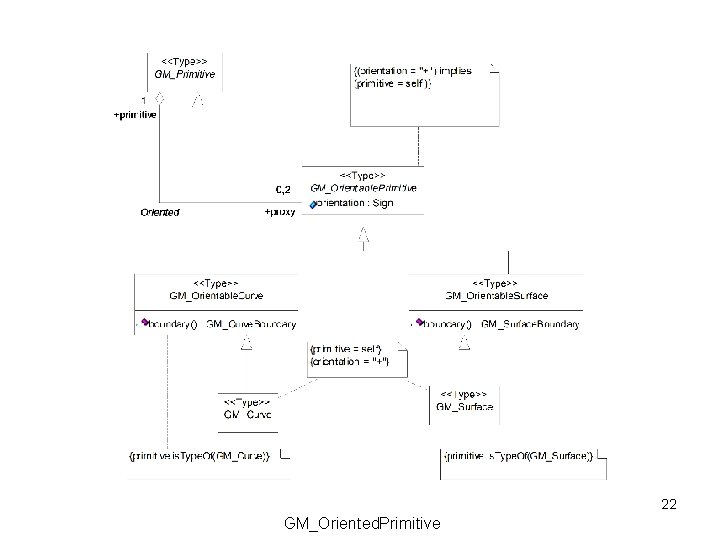
22 GM_Oriented. Primitive

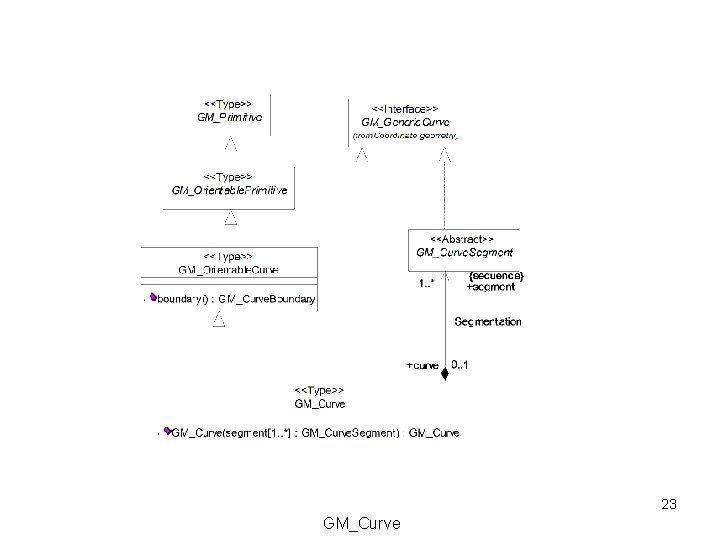
23 GM_Curve

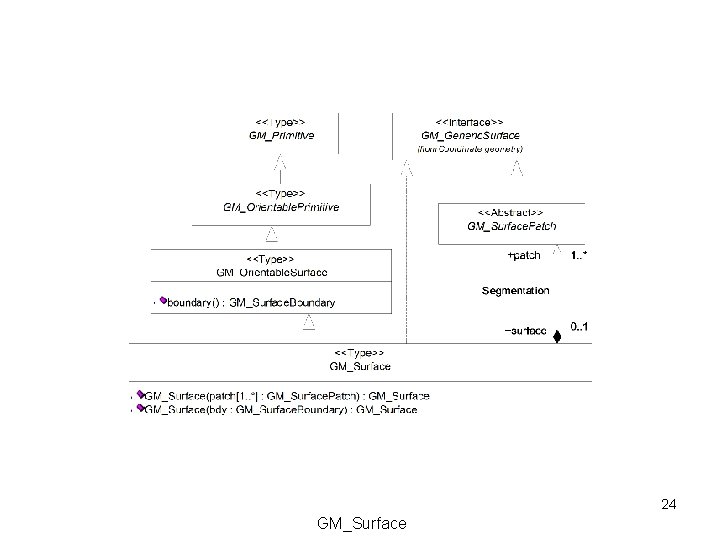
24 GM_Surface

25 GM_Solid

Coordinate Geometry

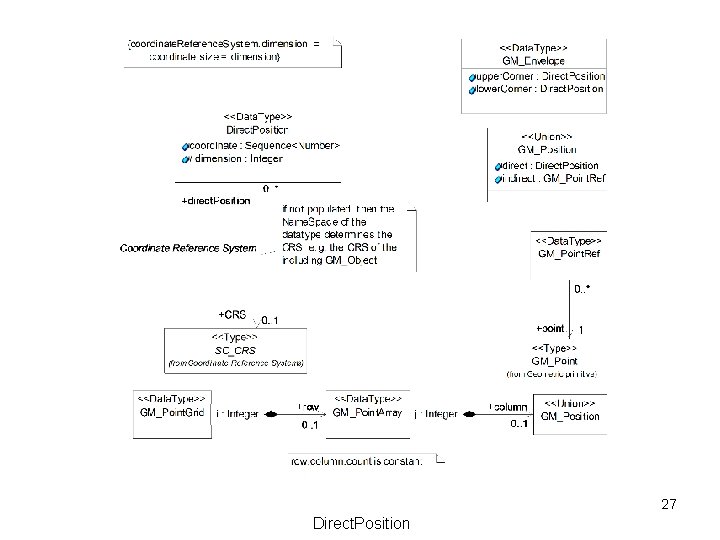
27 Direct. Position

28 Curve segment classes

29 Linear and Geodetic Interpolation

30 Arcs

31 Conics and placements

32 Spline and specialty curves

33 Surface patches

34 Polygonal surface

35 TIN construction

36 GM_Parmetric. Curve. Surface and its subtypes

Geometric Aggregate Geometric Complex

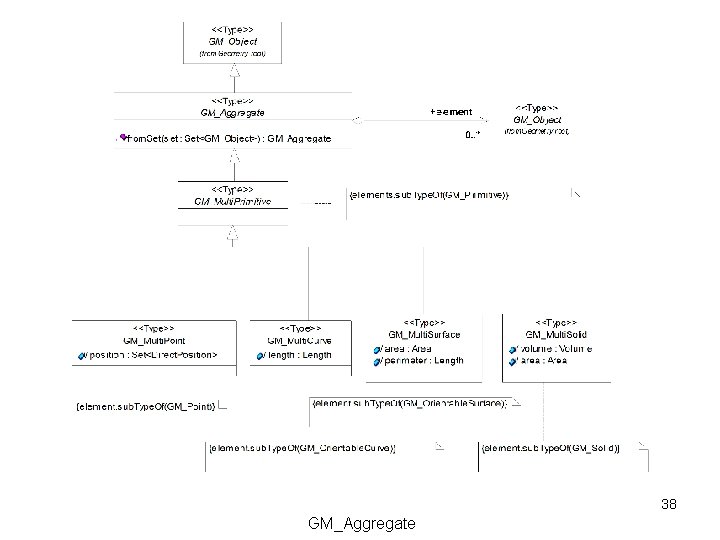
38 GM_Aggregate

39 GM_Complex

40 CM_Composite

Topology

Concept of Topology • Topology – Deal with characteristics of geometric figures that remain invariant if the space is deformed elastically and continuously – E. g. connectivity of an n-dimensional graph 42

43 Topology packages

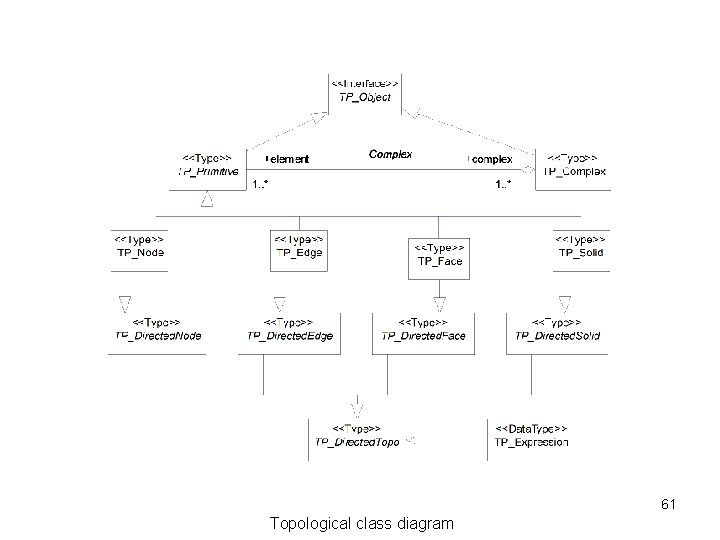
44 Topological class diagram

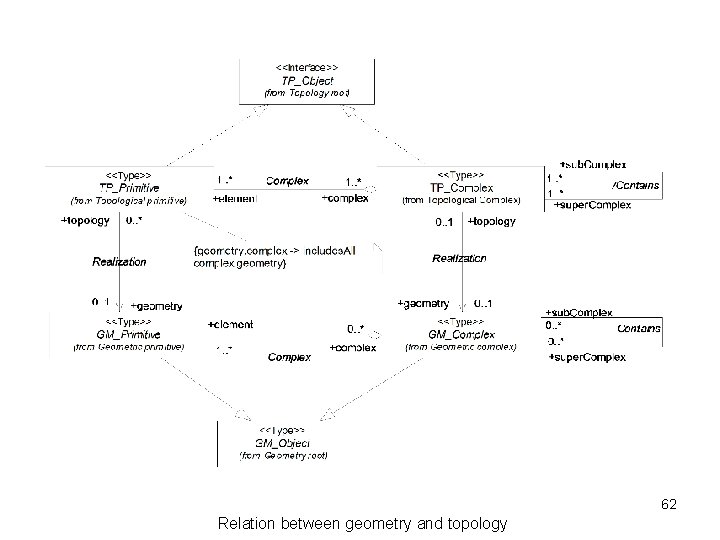
45 Relation between geometry and topology

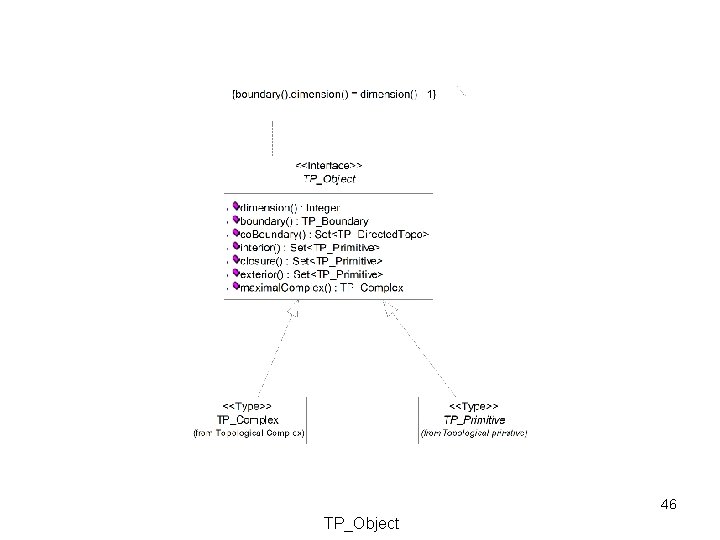
46 TP_Object

47 Boundary and coboundary operation

48 Boundary relation data types

49 TP_Primitive

50 TP_Directed. Topo subclasses

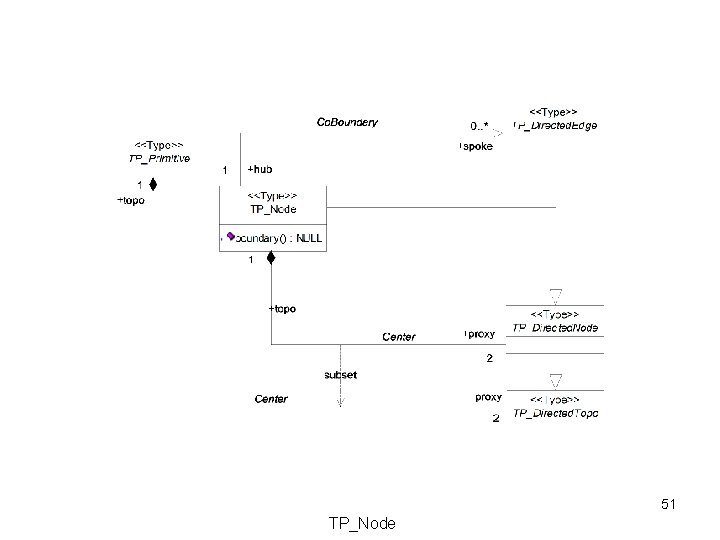
51 TP_Node

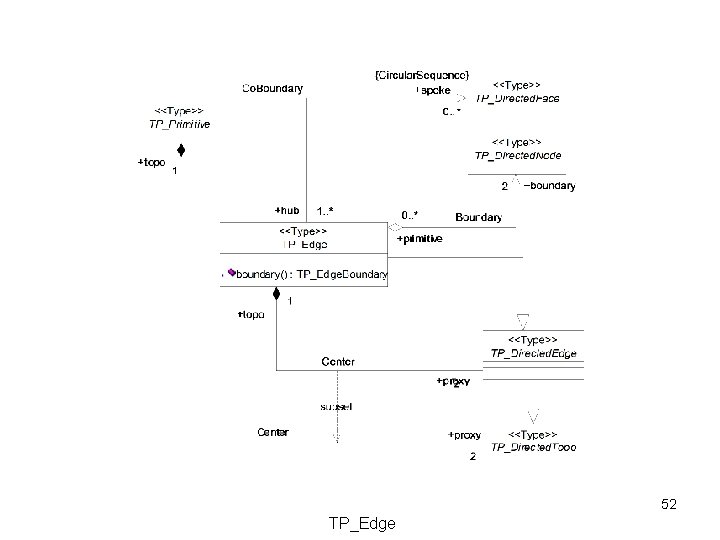
52 TP_Edge

53 TP_Face

54 TP_Solid

55 TP_Expression

56 TP_Complex

Summary

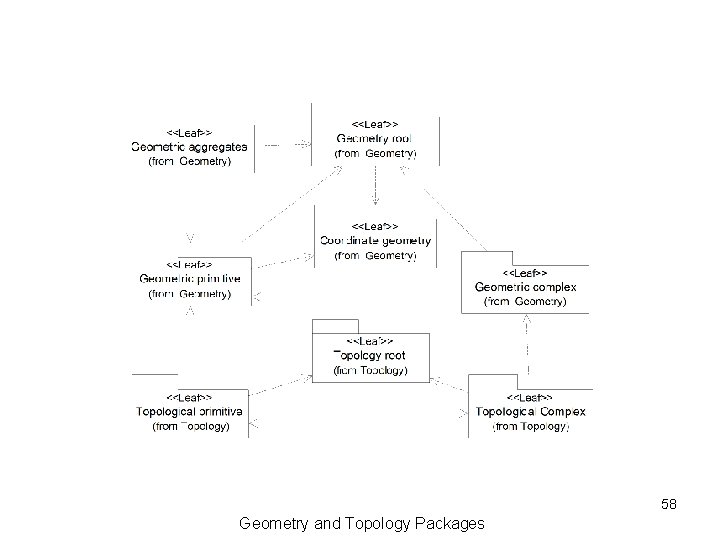
58 Geometry and Topology Packages

59 Geometry basic classes

60 Geometry Boundary Data Types

61 Topological class diagram

62 Relation between geometry and topology

Spatial Examples from ISO 19107

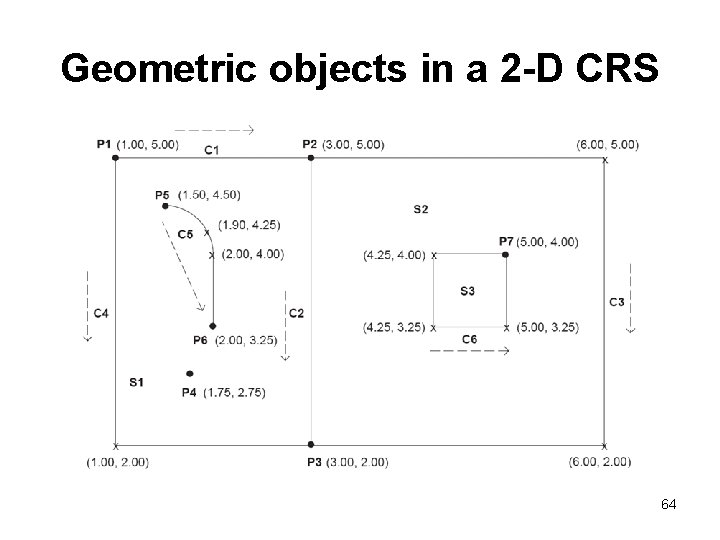
Geometric objects in a 2 -D CRS 64

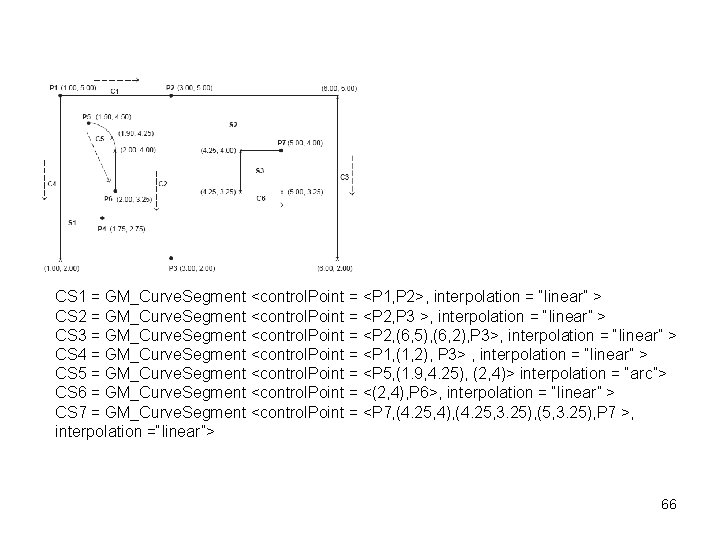
P 1 = GM_Point < position = < 1. 00, 5. 00 > > P 2 = GM_Point < position = < 3. 00, 5. 00 > > P 3 = GM_Point < position = < 3. 00, 2. 00 > > P 4 = GM_Point < position = < 1. 75, 2. 75 > > P 5 = GM_Point < position = < 1. 50, 4. 50 > > P 6 = GM_Point < position = < 2. 00, 3. 25 > > P 7 = GM_Point < position = < 5. 00, 4. 00 > > 65

CS 1 = GM_Curve. Segment <control. Point = <P 1, P 2>, interpolation = “linear” > CS 2 = GM_Curve. Segment <control. Point = <P 2, P 3 >, interpolation = “linear” > CS 3 = GM_Curve. Segment <control. Point = <P 2, (6, 5), (6, 2), P 3>, interpolation = “linear” > CS 4 = GM_Curve. Segment <control. Point = <P 1, (1, 2), P 3> , interpolation = “linear” > CS 5 = GM_Curve. Segment <control. Point = <P 5, (1. 9, 4. 25), (2, 4)> interpolation = “arc”> CS 6 = GM_Curve. Segment <control. Point = <(2, 4), P 6>, interpolation = “linear” > CS 7 = GM_Curve. Segment <control. Point = <P 7, (4. 25, 4), (4. 25, 3. 25), (5, 3. 25), P 7 >, interpolation =“linear”> 66

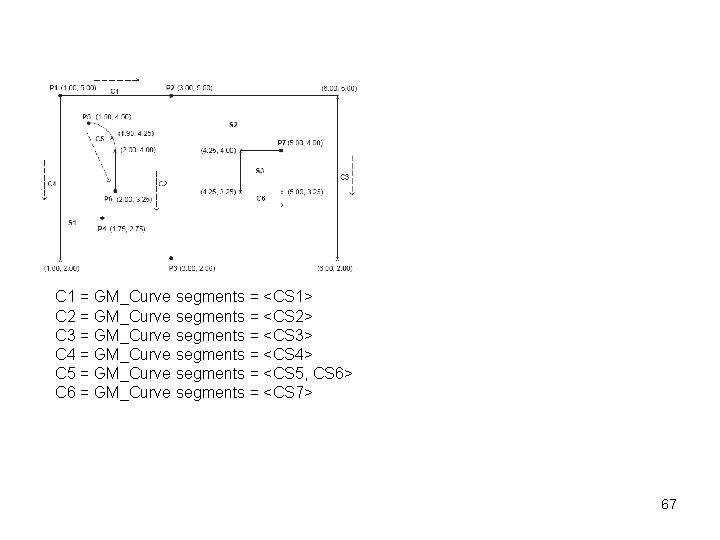
C 1 = GM_Curve segments = <CS 1> C 2 = GM_Curve segments = <CS 2> C 3 = GM_Curve segments = <CS 3> C 4 = GM_Curve segments = <CS 4> C 5 = GM_Curve segments = <CS 5, CS 6> C 6 = GM_Curve segments = <CS 7> 67

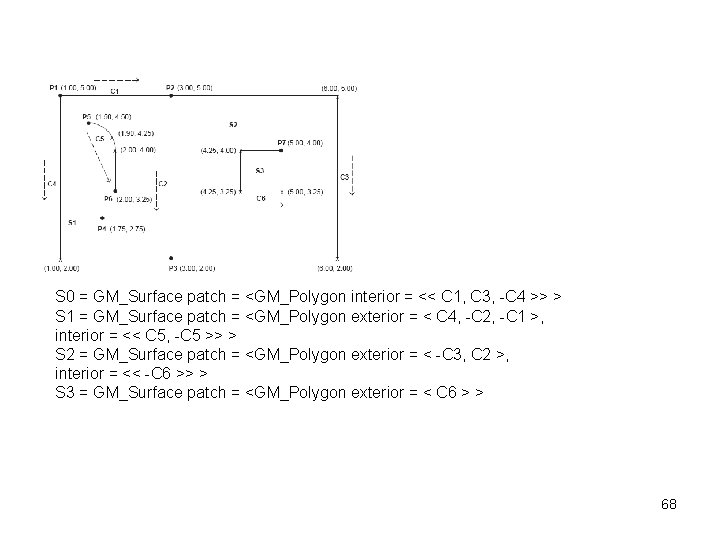
S 0 = GM_Surface patch = <GM_Polygon interior = << C 1, C 3, -C 4 >> > S 1 = GM_Surface patch = <GM_Polygon exterior = < C 4, -C 2, -C 1 >, interior = << C 5, -C 5 >> > S 2 = GM_Surface patch = <GM_Polygon exterior = < -C 3, C 2 >, interior = << -C 6 >> > S 3 = GM_Surface patch = <GM_Polygon exterior = < C 6 > > 68

Lake = Area. Feature feature. Type=“Hydrography: : Water. Body”, extent = S 3 Road. Centerline = Line. Feature feature. Type = “Transportation: : Road”, centerline = C 2 Road. Area = Road. Center. Line. centerline. buffer < distance = 10 m > Road. Extent = Area. Feature feature. Type = “Land. Cover: : Road”, extent = Road. Area Road. Instance = Complex. Feature feature. Type = “Land. Use: : Road”, feature. Components = {Road. Centerline, Road. Area } Trail = Line. Feature feature. Type = “Cultural. Facilities: : Hiking. Trail”, centerline = C 5 School = Point. Feature feature. Type = “Cultural. Facilities: : School”, Location = P 4 69