Ishodi uenja u nastavi matematike Jelena Horvat prof

Ishodi učenja u nastavi matematike Jelena Horvat, prof. OŠ Veliki Bukovec, 20. travnja 2010.

Što su ishodi učenja? �tvrdnje o tome što se očekuje od učenika da zna, razumije, može napraviti. . . kao posljedice učenja znanja, vještine, vrijednosti �NISU – skup zapamćenih činjenica, sadržaji koje učenici moraju usvojiti �definiraju ih nastavnici, ali su usmjereni na aktivnost učenika

Važnost definiranja ishoda učenja �učiteljima – određivanje sadržaja, aktivnosti, način vrednovanja �učenicima – jasan okvir i očekivanja �roditeljima – jasnija slika o radu njihove djece, osnova za praćenje napredovanja

Kompetencije �kompetencija – lat. competentia = postizati, biti sposoban �stručna sposobnost kojom pojedinac raspolaže; mjerodavnost �Europski parlament – 8 ključnih kompetencija za cjeloživotno učenje

Matematička kompetencija �sposobnost razvoja i primjene matematičkog mišljenja u svakodnevnom životu �uključuje = vladanje brojevima, znanje, aktivnost �matematički način mišljenja (logika, prostorno mišljenje, rasuđivanje), prikazivanje (grafikoni, tabele. . . )

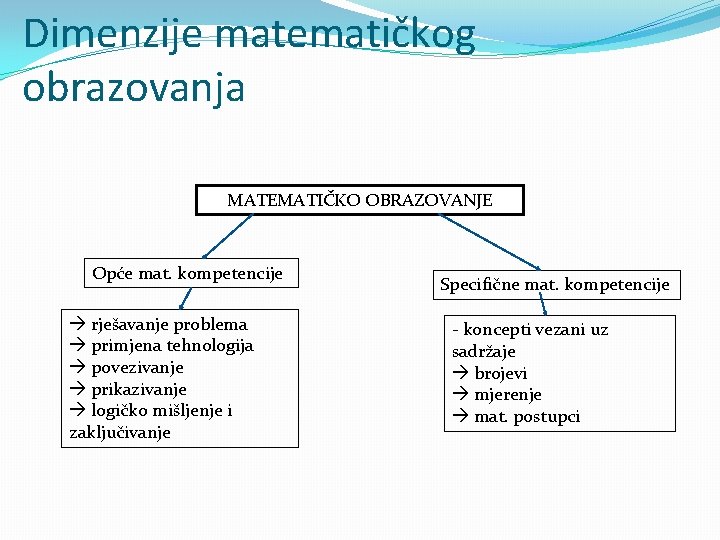
Dimenzije matematičkog obrazovanja MATEMATIČKO OBRAZOVANJE Opće mat. kompetencije rješavanje problema primjena tehnologija povezivanje prikazivanje logičko mišljenje i zaključivanje Specifične mat. kompetencije - koncepti vezani uz sadržaje brojevi mjerenje mat. postupci

Kognitivna domena ishoda učenja �Benjamin Bloom, 1956. �tri domene – kognitivna (znanje), afektivna (stavovi), psihomotorička (vještine) � 6 hijerarhijskih razina – poredane po složenosti

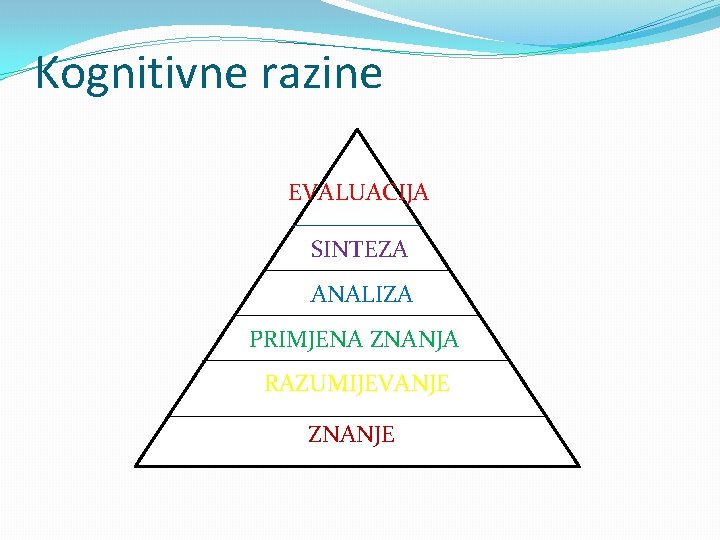
Kognitivne razine EVALUACIJA SINTEZA ANALIZA PRIMJENA ZNANJA RAZUMIJEVANJE ZNANJE

ZNANJE �znanje – reprodukcija činjenica, prisjećanje �ključne riječi – nacrtaj, pronađi, upari, pročitaj �primjeri: Što je kružnica? Nacrtaj pravac p i na njemu označi točku A. Nabroji nekoliko geometrijskih likova.

RAZUMIJEVANJE �usporedba, interpretacija svojim riječima, procjenjivanje �ključne riječi – usporedi, pokaži, prepoznaj, izrazi, predvidi, opiši �primjeri: Koji će zbroj biti veći, 10 + 3 ili 100 + 3? Je li nacrtani lik krug ili kružnica i zašto?

PRIMJENA ZNANJA �rješavanje problema, primjena starih znanja u novim situacijama �ključne riječi: preračunaj, otkrij, prouči, protumači �primjeri: Ako znamo kako se zbrajaju dva dvoznamenkasta broja, kako ćemo zbrojiti dva troznamenkasta broja?

ANALIZA �razumijevanje strukture problema �ključne riječi: razluči, usporedi, razlikuj, rastavi, zaključi �primjer: problemski zadatak riječima – npr. zbroju najmanjeg dvoznamenkastog i najvećeg troznamenkastog broja dodaj razliku najmanjeg troznamenkastog i najmanjeg dvoznamenkastog broja.

SINTEZA �stvaranje informacije na temelju skupljenih podataka �ključne riječi – predloži, uredi, organiziraj, poveži �primjer: Sastavi zadatak riječima za svog prijatelja iz klupe.

EVALUACIJA �procjena o korisnosti ideja i materijala �ključne riječi – usporedi, zaključi, prosudi, objasni �primjer: Kako bi ovo što si danas naučio objasni svojoj mlađoj sestri? Što bi joj rekao, zašto je to znanje korisno?

Obrazovni ishodi POŽELJNI GLAGOLI NEPOŽELJNI GLAGOLI definirati znati analizirati razumjeti usporediti cijeniti napraviti usvojiti Razlikovati naučiti opisati osvijestiti aktivne i mjerljive aktivnosti pasivne i nemjerljive aktivnosti izbjegavati riječi “bolje” i “više” jer podrazumijevaju mjerenje koristiti se Bloomovom taksonomijom

Primjer – matematika u NOK-u � C. Logičko mišljenje, argumentiranje i zaključivanje 1. ciklus � Učenici će moći: C 1. postavljati matematici svojstvena pitanja (Koliko ima. . . ? Što je poznato? Što trebamo odrediti? Kako ćemo odrediti? Zbog čega? Imali rješenje smisla? Postoji li više rješenja? i dr. ), te stvarati i istraživati pretpostavke o matematičkim objektima, pravilnostima i odnosima, C 2. obrazložiti odabir matematičkih postupaka i utvrditi smislenost dobi -venoga rezultata, C 3. zaključivati nepotpunom indukcijom i neformalnom dedukcijom s malim brojem koraka.

Primjer – matematika u NOK-u � E. Primjena tehnologije � 1. ciklus Učenici će moći: E 1. istraživati i učiti matematiku pomoću džepnih računala i primjerenih obrazovnih računalnih programa. � 2. ciklus Učenici će moći: E 1. istraživati i učiti matematiku pomoću džepnih računala i primjerenih računalnih programa, E 2. rabiti tehnologiju za crtanje, za prikupljanje, organiziranje i prikazivanje podataka i informacija, te u situacijama kojima su u središtu interesa matematičke ideje (u svrhu rasterećivanja od računanja).

Da ponovimo. . . 1. pitati se što učenici trebaju znati i biti u stanju činiti 2. koristiti jasne i konkretne glagole usmjerene na aktivnost učenika 3. obuhvatiti područja znanja, vještina i stavova 4. obuhvatiti sve razine Bloomove taksonomije

Da ponovimo. . . �poželjni aktivni glagoli učenici će nakon ovoga sata moći usporediti, razlikovati, izračunati, napraviti, odabrati. . . • nepoželjni su suviše općeniti glagoli učenici će nakon ovog sata znati, naučiti, razumjeti, cijeniti. . .

Izvori � http: //www. matematika. hr/_download/repository/Ucenicka_postignu ca_OS_04062009. pdf � http: //web. math. unizg. hr/nastava/metodika/materijali/mnm 3 Bloomova_taksonomija-ishodi. pdf � http: //www. unizg. hr/fileadmin/rektorat/slike/zvonimira/ishodi_ucenj a/Ishodi_ucenja-Vjeran_Strahoja. pdf � http: //www. matematika. hr/_download/repository/Matematika-NOKpredavanje-Zagreb. pdf � http: //pil 2. mscommunity. net/Portals/0/sadrzaj/elearning/learning 2_novo/bloom_dr_lek. htm � http: //www. sos. net/~donclark/hrd/bloom. html