Isentropic Flow Examples of Isentropic Flow Diffusers Air

Isentropic Flow

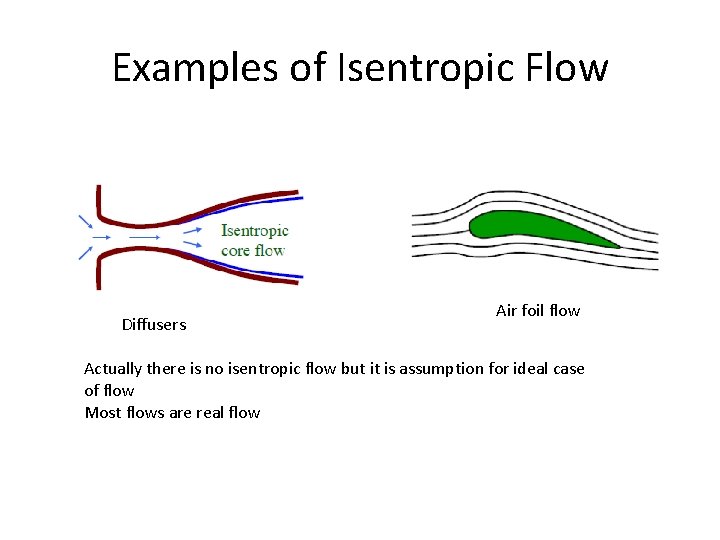
Examples of Isentropic Flow Diffusers Air foil flow Actually there is no isentropic flow but it is assumption for ideal case of flow Most flows are real flow

Definition of Isentropic Flow Isentropic flow : the flow which the properties of it at any location or any time could be estimated According to the isentropic process equation

ISENTROPIC Process Governing Equation • Goal: Relate Thermodynamics to Compressible Flow • Adiabatic Process: No heat is added or removed from system – dq = 0 – Note: Temperature can still change because of changing density • Reversible Process: No friction (or other dissipative effects) • Isentropic Process: (1) Adiabatic + (2) Reversible – (1) No heat exchange + (2) no frictional losses – Relevant for compressible flows only – Provides important relationships among thermodynamic variables at two different points along a streamline g = ratio of specific heats g = cp/cv gair=1. 4

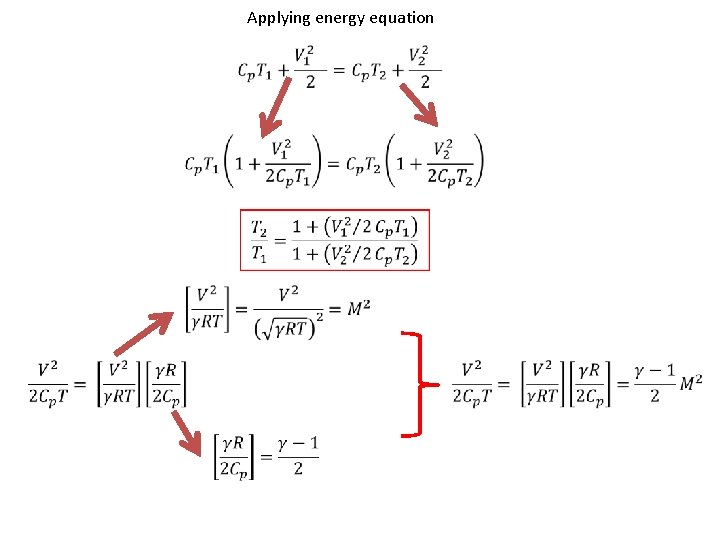
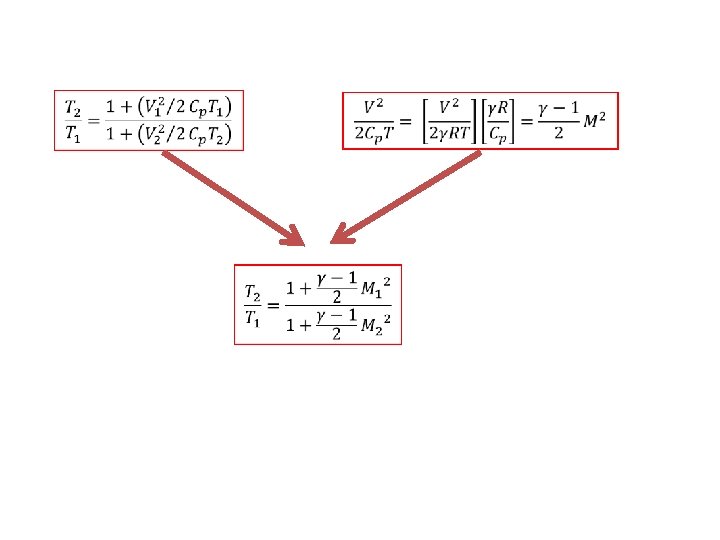
ENERGY EQUATION SUMMARY • Energy can neither be created nor destroyed; can only change physical form – Same idea as 1 st law of thermodynamics Energy equation for frictionless, adiabatic flow (isentropic) h = enthalpy = e+p/r = e+RT h = cp. T for an ideal gas Also energy equation for frictionless, adiabatic flow Relates T and V at two different points along a streamline

SPEED OF SOUND • Sound waves travel through air at a finite speed • Sound speed (information speed) has an important role in aerodynamics • Combine conservation of mass, Euler’s equation and isentropic relations: • Speed of sound, a, in a perfect gas depends only on temperature of gas • Mach number = flow velocity normalizes by speed of sound – If M < 1 flow is subsonic – If M = 1 flow is sonic – If M > flow is supersonic • If M < 0. 3 flow may be considered incompressible

GOVERNING EQUATIONS STEADY AND INVISCID FLOW • Incompressible flow of fluid along a streamline or in a stream tube of varying area • Most important variables: p and V • T and r are constants throughout flow • Compressible, isentropic (adiabatic and frictionless) flow along a streamline or in a stream tube of varying area • T, p, r, and V are all variables continuity isentropic energy equation of state at any point continuity Bernoulli

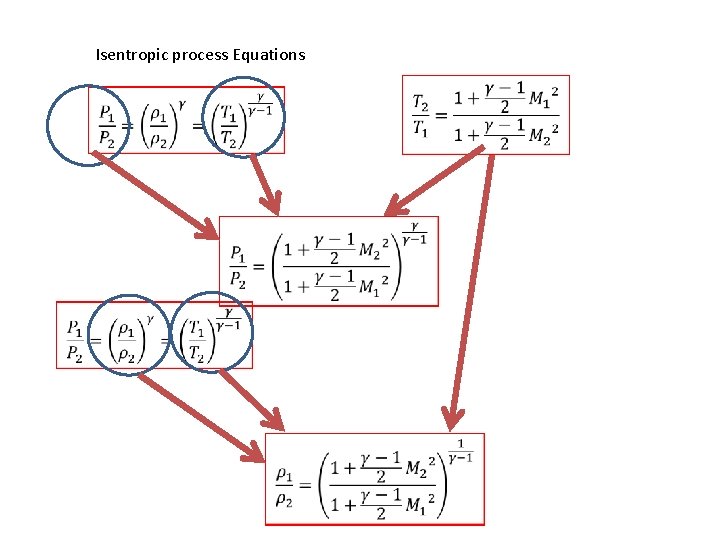
Derivation of Isentropic Flow Equations Isentropic governing equation 1 Speed of sound 2 By combining Eq 1 and Eq 2 3

Applying energy equation

Isentropic process Equations

Compressible flow Equation Referred to Stagnation Conditions At stagnation condition the velocity is zero For Any two point on flow stream For any point on flow stream and stagnation point

Compressible flow Equation Referred to Critical Conditions At critical conditions the velocity is equal to speed of sound For Any two point on flow stream For critical point of flow stream and stagnation point