ISA 562 Information Security Theory Practice Public Key

ISA 562 Information Security Theory & Practice Public Key Cryptosystem Chapter 9 of Bishop’s Book 1

Outline n n Background Diffie-Hellman RSA Cryptographic Checksums 2

History n n n Concept conceived by Diffie and Hellman in 1976 Rivest, Shamir and Adleman (RSA) were first to describe a public key system in 1978 Merkle and Hellman published a different solution later in 1978 (broken by Shamir) 3

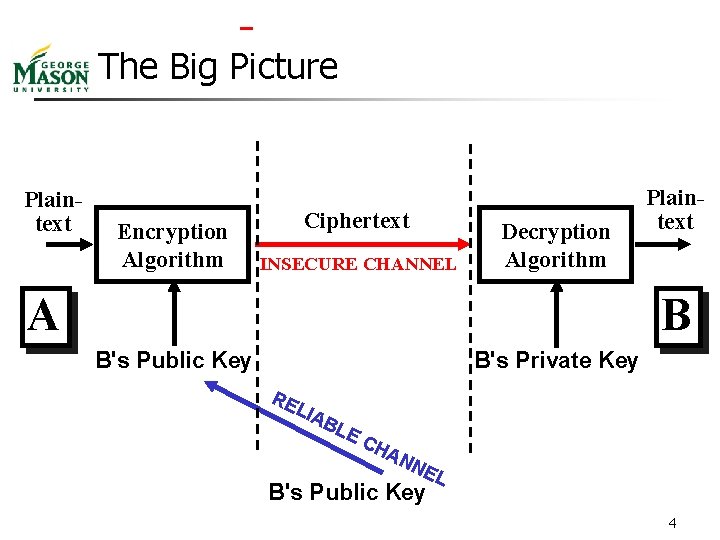
The Big Picture Plaintext Encryption Algorithm Ciphertext INSECURE CHANNEL Decryption Algorithm A Plaintext B B's Public Key B's Private Key RE LIA BL E CH AN NE B's Public Key L 4

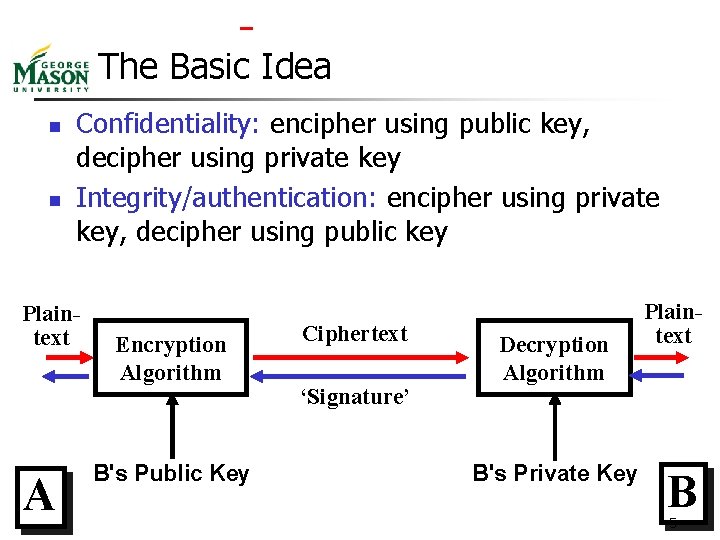
The Basic Idea n n Confidentiality: encipher using public key, decipher using private key Integrity/authentication: encipher using private key, decipher using public key Plaintext A Encryption Algorithm B's Public Key Ciphertext ‘Signature’ Decryption Algorithm B's Private Key Plaintext B 5

Requirements n The keys and algorithms must meet these requirements n n n Must be computationally easy to encipher or decipher Must be computationally infeasible to derive the private key from the public key Must be computationally infeasible to determine the private key from a chosen plaintext attack Different from those of secret key cryptosystem except the first requirement Why another cryptosystem? 6

Motivation 1 - Key Distribution Problem n n In a secret key cryptosystem, the secret key must be transmitted via a secure channel Inconvenient n n Insecure n n n parties want to communicate with each other, how many keys need to be transmitted? Is the secure channel really secure? Public key cryptosystem solves the problem n n Public key known by everyone – telephone directory Privacy key is never transmitted 7

Motivation 2 - Digital Signature n n In a secret key cryptosystem, authentication and non-repudiation may be difficult Authentication n n Non-repudiation n n You must share a secret key with someone in order to verify his signature “I didn’t sign it. You did since you also have the key” Public key cryptosystem solves the problem n n Verification of signature needs only the public key One is solely responsible for his private key 8

Required number theory n If a = b + kn for some integer k n n n We write b = a mod n (namely, a is congruent to b modulo n, and b is the residue of a modulo n) Examples: 2 = 12 mod 5, 2 = 12 mod 10, 0 = 12 mod 6 Properties (a O b) mod n = ((a mod n) O (b mod n)) mod n where O is +, -, * 35 mod 7 = (3*3*3 mod 7) = ((3*3 mod 7)*(3 mod 7))mod 7 Needed when enciphering/deciphering 9

More of the same… n A prime number is a positive integer having exactly one positive divisor other than 1. E. g. 3, 5, 7, 11, 13… n n a and b are relatively prime if they have no common positive factors other than 1. E. g. 1 and 2, 2 and 3, 3 and 4, but not 2 and 4 The totient function (n) gives the number of integers between 1 and n-1 that are relatively prime to n. E. g. (10) = 4 (1, 3, 7, 9 are relatively prime to 10) 10

Still More Math n Euler's Totient Theorem n n n 1 = a (n) mod n, where a and n are relatively prime Example: 3 (10) mod 10= 3 4 mod 10 = 81 mod 10 10 (3) mod 3= 10 2 mod 3 = 100 mod 3 Fermat’s Little Theorem n n a p-1=1 mod p, where p is prime and relatively prime to a Notice (p) = p-1 11

Outline n n Background Diffie-Hellman RSA Cryptographic Checksums 12

Diffie-Hellman Key Exchange Scheme n n n Proposed in 1976 as the first public key algorithm (predates RSA) Allows users to agree on a secret key over insecure channels with no prior communication The secret key can thus be used to encrypt or decrypt message (e. g. , SSL 3. 0, IPsec) A K Insecure Channel B 13

Discrete Logarithm Problem n D-H is based on the discrete logarithm problem n n n Given integers n and g and prime number p, compute k such that n = g k mod p In general computationally infeasible Choices for g and p are critical n n n Both p and (p– 1)/2 should be prime p should be large (at least 512 bits, possibly 1028 bits) g should be a primitive root mod p 14

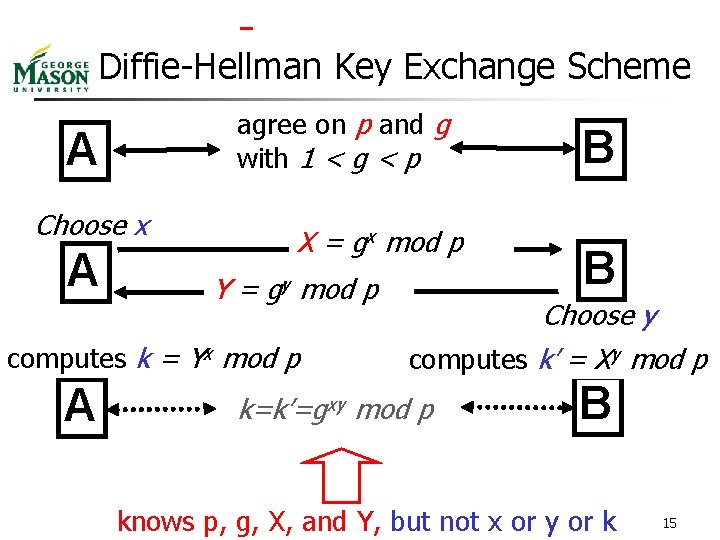
Diffie-Hellman Key Exchange Scheme agree on p and g with 1 < g < p A Choose x A X = gx mod p Y= gy mod p computes k = Yx mod p A B B Choose y computes k’ = Xy mod p k=k’=gxy mod p B knows p, g, X, and Y, but not x or y or k 15

Quiz n p = 7 and g = 5 n Alice n n n Bob n n n chooses x = 2 and send X = ? chooses y = 3 and send Y = ? Shared key: n n n k= ? k’ = ? (gxy mod p = ? ) 16

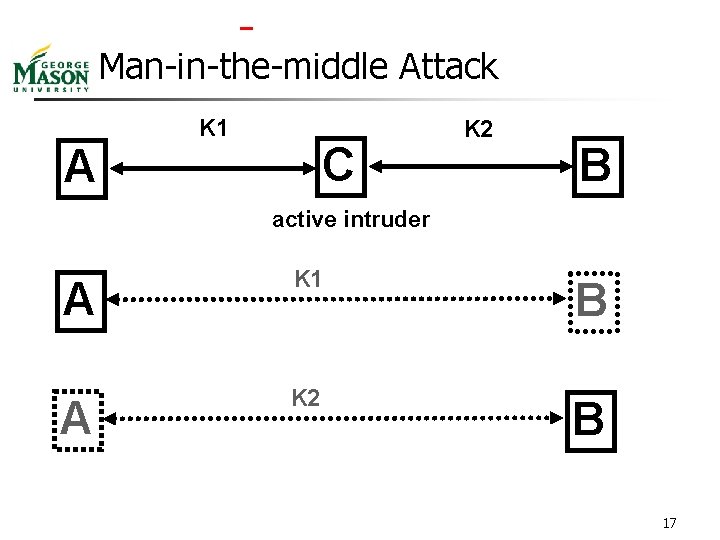
Man-in-the-middle Attack K 1 C A K 2 B active intruder A K 1 B A K 2 B 17

Outline n n Background Diffie-Hellman RSA Cryptographic Checksums 18

RSA In Summary n n Choose public key (n, e) Compute private key (n, d) Key Generation n Encryption C = Me mod n Decryption M = Cd mod n n Underlying theory – Euler's Totient Theorem n 19

Key Generation n Choose 2 large (512 bit) prime numbers p and q Compute n = p * q n Choose e relatively prime to (p-1)*(q-1) n Compute d such that 1 = e*d mod (p-1)*(q-1) n Publish (n, e) and keep (n, d) (discard p, q) n 20

Key Generation (Cont’d) n n n Large primes can be found efficiently using probabilistic algorithms due to Solvay and Strassen d can be computed using the Extended Euclidean Algorithm (Textbook 31. 2) Care must be exercised in choosing p and q, otherwise insecurities may result (p-1, p+1, q-1, q+1 should have large prime factors) 21

Key Generation - Example n n n p = 7, q = 11, so n = 77 and (p-1)(q-1) = 60 Alice chooses e = 17, computing d = 53 (17*53=901) publish (77, 17) and keep (77, 53) secret 22

Encryption/Decription n Encryption C = Me mod n Decryption M = Cd mod n n Underlying theory n n Cd mod n = (Me mod n)d mod n = Med mod n = M 1 mod (p-1)*(q-1) mod n = M (p-1)*(q-1)*i + 1 mod n = (1 i *M) mod n (by Fermat’s Little Theorem) = M mod n =M (require M<n; M relatively prime to n) 23

Example: Encryption n p = 7, q = 11, n = 77 Alice chooses e = 17, making d = 53 n Bob wants to send Alice secret message HELLO n (07 04 11 11 14) n n n 0717 0417 1117 1417 mod mod mod 77 77 77 = = = 28 16 44 44 42 Bob sends 28 16 44 44 42 24

Example: Decryption n n Alice receives 28 16 44 44 42 Alice uses private key, d = 53, to decrypt message: n n n 2853 1653 4453 4253 mod mod mod 77 77 77 = = = 07 04 11 11 14 Alice translates 07 04 11 11 14 to HELLO n No one else could read it, as only Alice knows her private key and that is needed for decryption 25

Digital Signatures in RSA n n RSA has an important property, not shared by other public key systems Encryption and decryption are symmetric n n n Encryption followed by decryption yields the original message (Me mod n)d mod n = M Decryption followed by encryption also yields the original message (Md mod n)e mod n = M Because e and d are symmetric in e*d = 1 mod (p-1)*(q-1) 26

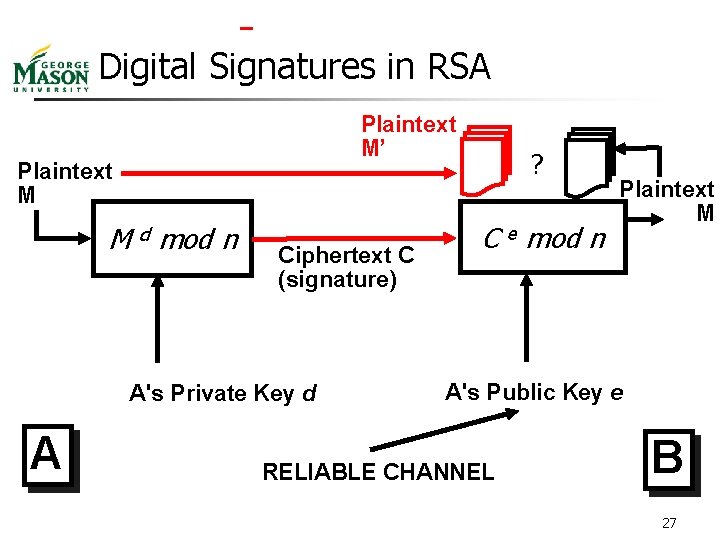
Digital Signatures in RSA Plaintext M’ Plaintext M M d mod n Ciphertext C (signature) A's Private Key d A ? C e mod n Plaintext M A's Public Key e RELIABLE CHANNEL B 27

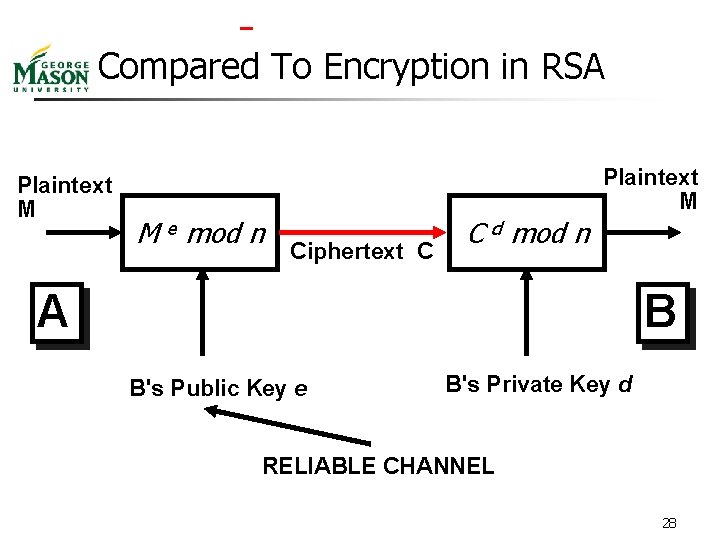
Compared To Encryption in RSA Plaintext M M e mod n Ciphertext C C d mod n A B B's Public Key e B's Private Key d RELIABLE CHANNEL 28

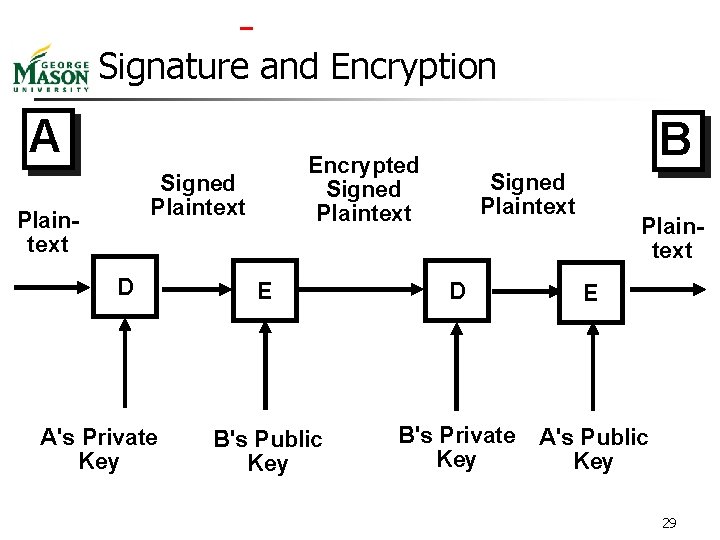
Signature and Encryption A Encrypted Signed Plaintext D A's Private Key B Signed Plaintext E D E B's Public Key B's Private Key A's Public Key 29

Signature and Encryption n n We could do the encryption first followed by the signature. Signature first has the advantage that the signature can be verified by parties other than B. 30

Example: Sign n Take p = 7, q = 11, n = 77 Alice chooses e = 17, making d = 53 Alice wants to send Bob message HELLO (07 04 11 11 14) so Bob knows it is from Alice, and it has not been modified in transit n n n 0753 0453 1153 1453 mod mod mod 77 77 77 = = = 35 09 44 44 49 Alice sends 35 09 44 44 49 31

Example: Verify n n Bob receives 35 09 44 44 49 Bob uses Alice’s public key, e = 17, n = 77, to decrypt message: n n n 3517 0917 4417 4917 mod mod mod 77 77 77 = = = Bob translates n n 07 04 11 11 14 to HELLO (Assume) only Alice has her private key, so no one else could have been able to create a correct signature The (deciphered) signature matches the transmitted plaintext, so the plaintext is not altered 32

Example: Both n Alice wants to send Bob message HELLO both enciphered and signed n n n Alice does (does she encipher first or sign first? ) n n n n Alice’s keys: public (17, 77); private: 53 Bob’s keys: public: (37, 77); private: 13 (0753 (0453 (1153 (1453 mod mod mod 77)37 77)37 mod mod mod 77 77 77 = = = 07 37 44 44 14 Alice sends 07 37 44 44 14 What would Bob do upon receiving the message? 33

Security of RSA n Cryptanalysis is to compute d while knowing (e, n) n such that e*d = 1 mod (p-1)(q-1), and n=pq, for some p and q (the factorization is unique) n n n If factorization of n into p*q is known, this is easy (Extended Euclidean Algorithm). Otherwise, it is hard. Therefore security of RSA is no better than complexity of the factoring problem Is the factoring problem provably hard (e. g. , undecidable)? No n However, the possibility of an easy factoring method is believed to be remote. 34

RSA Versus DES n n n Fastest implementations of RSA can encrypt kilobits/second Fastest implementations of DES can encrypt megabits/second It is often proposed that RSA be used for secure exchange of DES keys This 1000 -fold difference in speed is likely to remain independent of technology advances Matters more in wireless/ad hoc/sensor network 35

RSA Versus DES n n n Key size of RSA is selected by the user Many implementations choose n to be 154 digits (512 bits) so the key (n, e) is 1024 bits Key size of DES is 64 bits (56 bits plus 8 parity bits) 36

RSA Key Size n n key size should be chosen conservatively cryptographers can stay ahead of (factorization) cryptanalysts by increasing the key size Until 1989 factorization attacks were based on "high school mathematics. " Since then sophisticated attacks have extended factorization to larger numbers (usually of a specific form). At present it appears that 130 digit numbers can be factored in several months using lots of idle workstations. 37

Outline n n Background Diffie-Hellman RSA Cryptographic Checksums 38

One-way Hash Functions n n Also known as message digest A function H(M) = m satisfies n n n (Fixed length): M can be of any length, whereas m is of fixed length (One-way): computing H(M)=m is easy, but computing H-1(m)=M is computationally infeasible (Collision-free): in two forms n n Weak collision-freedom: given any M, difficult to find another M’ such that H(M)=H(M’) Strong collision-freedom: difficult to find any M and M’ such that H(M)=H(M’) 39

Why Those Requirements? n Many applications store H(p) instead of a password p n n Fixed length: cannot guess the length of p from H(p) (and H(p) is easier to store) One-way: the administrator cannot learn p of others Collision-free: cannot submit incorrect p matching H(p) Most applications sign H(M) instead of M 40

Example n ASCII parity bit n n ASCII has 7 bits; 8 th bit is “parity” Even parity: even number of 1 bits Odd parity: odd number of 1 bits Bob receives “ 10111101” n If sender is using even parity; six ‘ 1’ bits, so character was received correctly n n Note: could be garbled, but 2 bits would need to have been changed to match parity bit If sender is using odd parity; even number of 1 bits, so character was not received correctly 41

Hash Functions In Practice n n n DES based hash functions tend to produce 64 bit digest which cannot be strong CCITT X. 509 (proven insecure) Merkle's Snefru: 2 -pass version proven insecure; 4 -pass version unproven Jueneman's methods: broken and refined and broken and refined NIST Secure Hash Algorithm RSA: MD 2, MD 4, MD 5, SHA-0, SHA-1, SHA-2 (SHA-224, SHA-256, SHA-384, and SHA-512 ) 42

“Hash Functions Broken” ? n Crypto 2004 Rump session reported attacks on MD 4, MD 5 and SHA-0 n n n MD 4’s attacks are done by hands Crypto 2005 reported attacks on full SHA-1 Should we panic? Xiaoyun Wang’s webpage: http: //www. infosec. sdu. edu. cn/people/wangxiaoyun. htm 43

“Hash Functions Broken” ? (Cont’d) n Nature of the results n Algorithm that finds collision faster than theoretic bound n n n Yes, the results disprove those functions to be strong collision-free No, they do not give you a password from its hash n n MD 5 about one hour; SHA-1 263 vs 280 (theoretically) Brute force attacks do (refer to http: //passcracking. com/) Whether you should panic or not depends on what you use the hash functions for Xiaoyun Wang’s webpage: http: //www. infosec. sdu. edu. cn/people/wangxiaoyun. htm 44

Hash Functions Vs MAC n Send a message M together with its hash h=H(M), so the recipient can verify M by comparing H(M) with the received h n n Attack: If anyone in the middle can replace M with M’ and h with h’=H(M’), the recipient won’t detect this Keyed hash functions n n Also known as message authentication codes (MAC) Example: DES in CBC mode: use a key to encipher message in CBC mode and use last n bits as the MAC value. 45

HMAC n Build MAC from keyless hash functions n Encryption algorithms cannot be exported n h : keyless hash function k : a cryptographic key k padded with 0 Ipad: 00110110 repeated Opad: 01011100 repeated n HMAC h(k, m) = h(k opad || h(k ipad || m)) n n exclusive or, || concatenation 46

Key Points n n Public key cryptosystems has two keys Diffie-Hellman exchanges secret key via insecure channel RSA can be used for confidentiality and integrity Cryptographic Checksums are keyed hash functions 47