Irregular to Completely Regular Meshing in Computer Graphics

Irregular to Completely Regular Meshing in Computer Graphics Hugues Hoppe Microsoft Research International Meshing Roundtable 2002/09/17

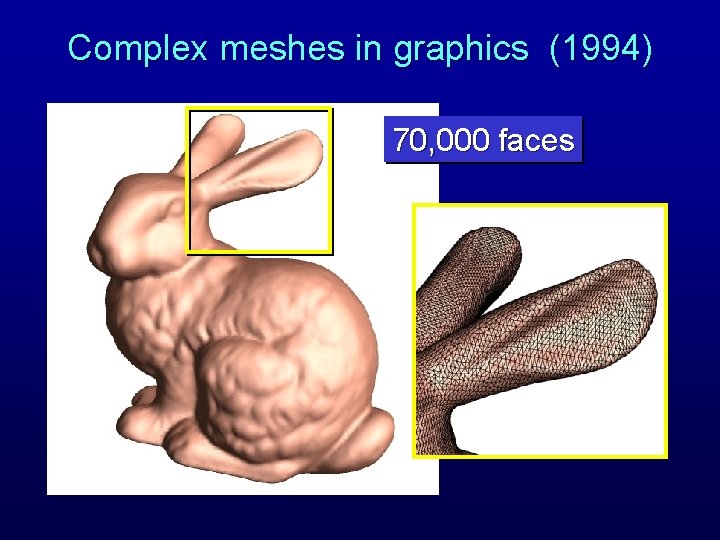
Complex meshes in graphics (1994) 70, 000 faces

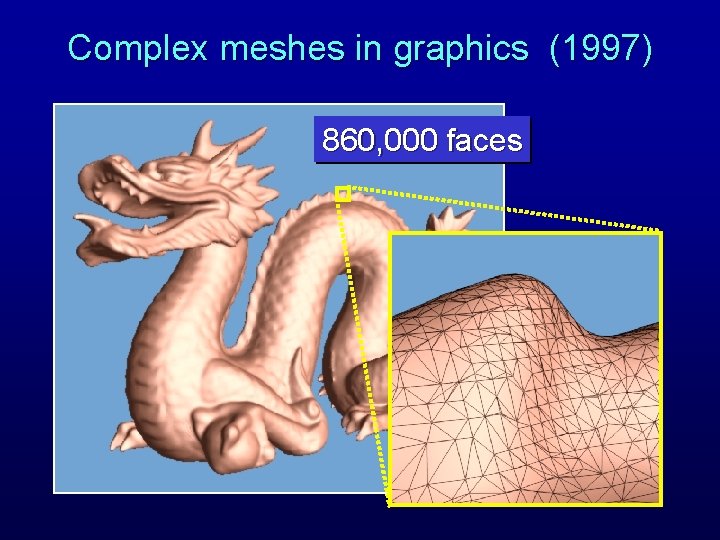
Complex meshes in graphics (1997) 860, 000 faces

Complex meshes in graphics (2000) 2, 000, 000 faces Challenges: - rendering - storage - transmission - scalability [Digital Michelangelo Project]

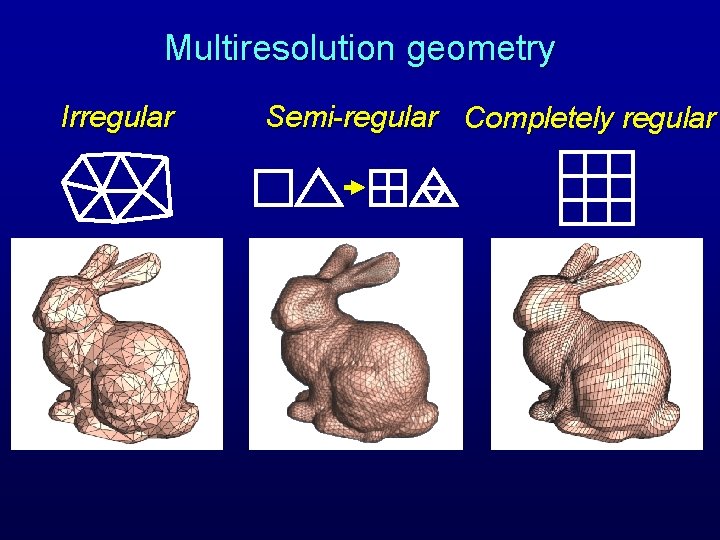
Multiresolution geometry Irregular Semi-regular Completely regular

Multiresolution geometry l Irregular meshes n n n l [1996] [1997] [2001] Semi-regular meshes n l Progressive meshes View-dependent refinement Texture-mapping PM Multiresolution analysis [1995] Completely regular meshes n Geometry images [2002]

Goals in real-time rendering #1 : Rendering speed n 60 -85 frames/second #2 : Rendering quality n n geometric “visual” accuracy temporal continuity Not a Goal: l Mesh “quality”

Not a goal: mesh quality 13, 000 faces 1, 000 faces

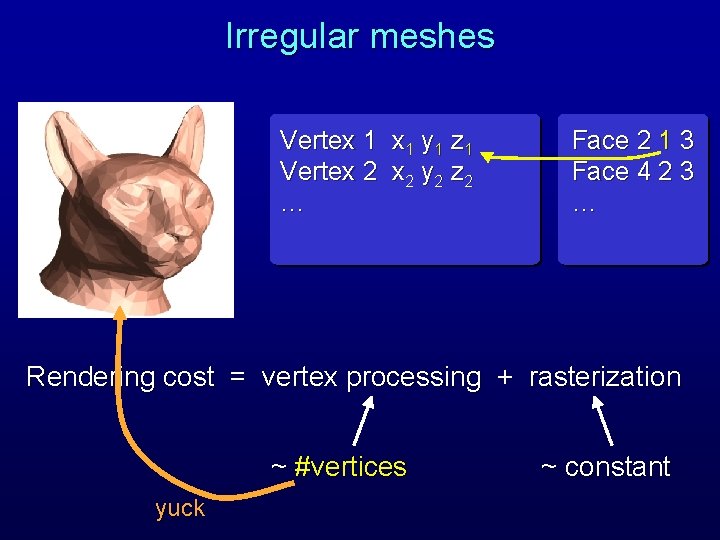
Irregular meshes Vertex 1 y 1 z 1 Vertex 2 y 2 z 2 … Face 2 1 3 Face 4 2 3 … Rendering cost = vertex processing + rasterization ~ #vertices yuck ~ constant

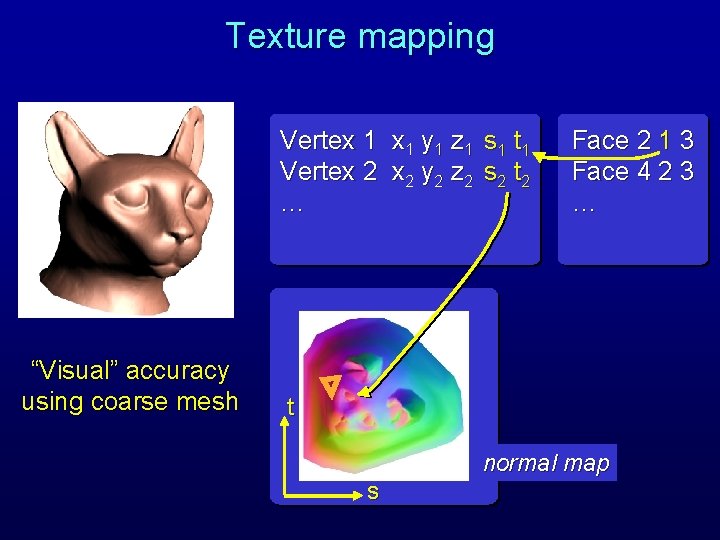
Texture mapping Vertex 1 y 1 z 1 s 1 t 1 Vertex 2 y 2 z 2 s 2 t 2 … “Visual” accuracy using coarse mesh Face 2 1 3 Face 4 2 3 … t normal map s

Goals in real-time rendering #1 : Rendering speed n Minimize #vertices best accuracy using irregular meshes #2 : Rendering quality n Use texture mapping parametrization

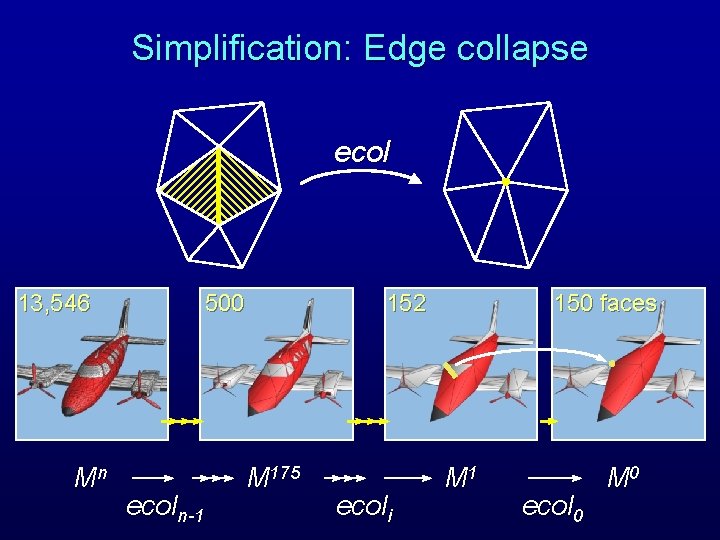
Simplification: Edge collapse ecol 13, 546 Mn 500 ecoln-1 152 M 175 ecoli 150 faces M 1 ecol 0 M 0

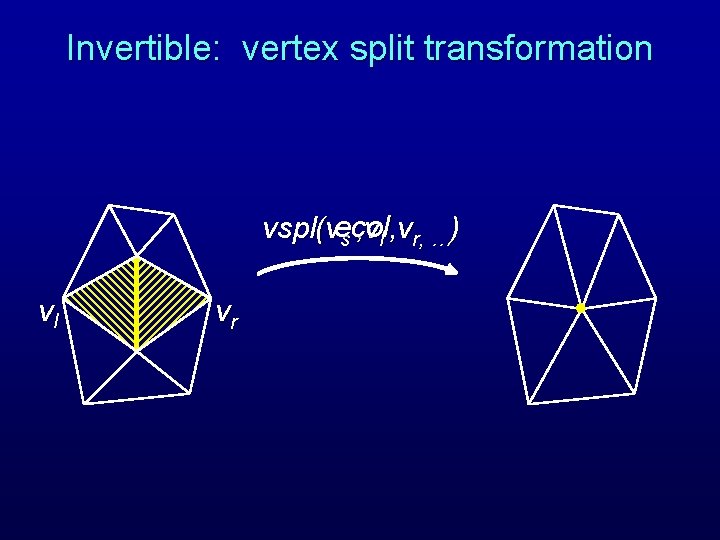
Invertible: vertex split transformation vspl(vecol s , vl , vr, …) vl vs vr

Progressive mesh 150 152 M 0 vspl 0 500 M 175 … … vspli i … … 13, 546 vspln-1 n-1 vspl progressive mesh (PM) representation Mn

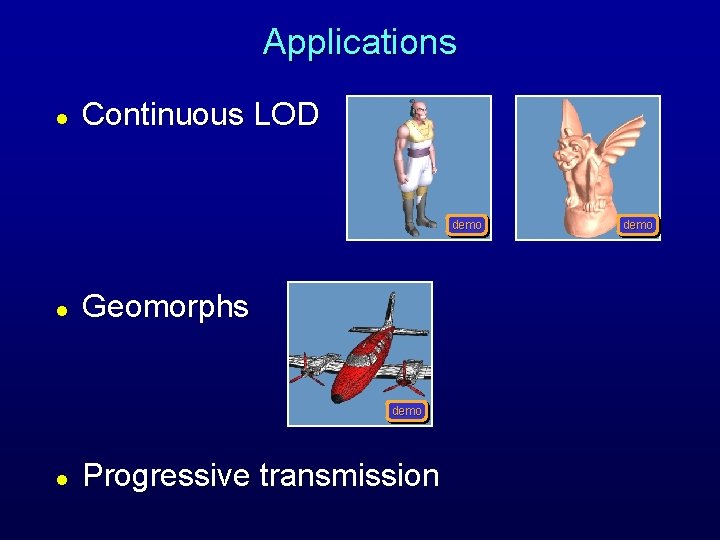
Applications l Continuous LOD demo l Geomorphs demo l Progressive transmission demo

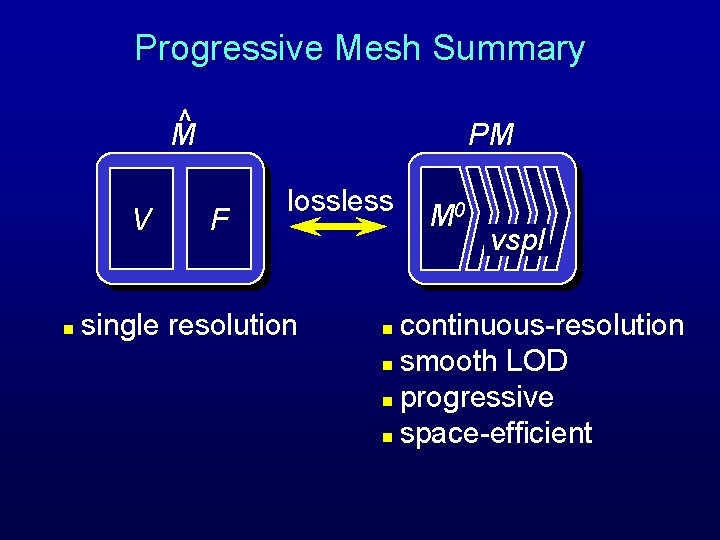
Progressive Mesh Summary ^ M V n PM F lossless single resolution M 0 vspl continuous-resolution n smooth LOD n progressive n space-efficient n

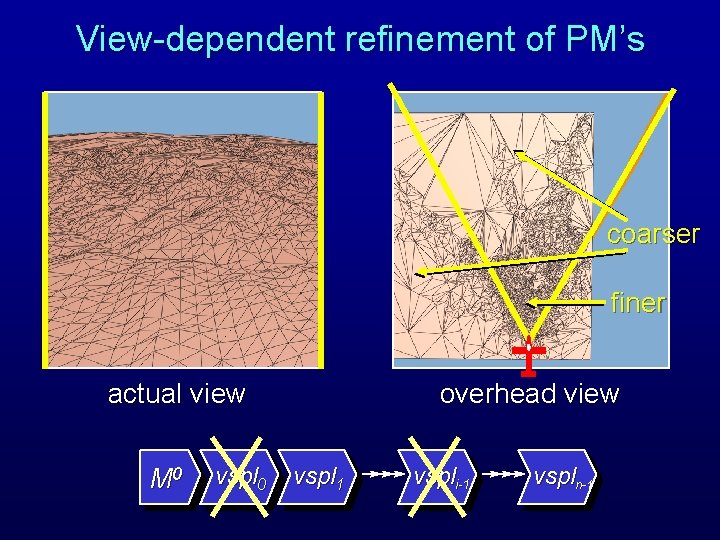
View-dependent refinement of PM’s coarser finer actual view M 0 vspl 0 overhead view vspl 1 vspli-1 vspln-1

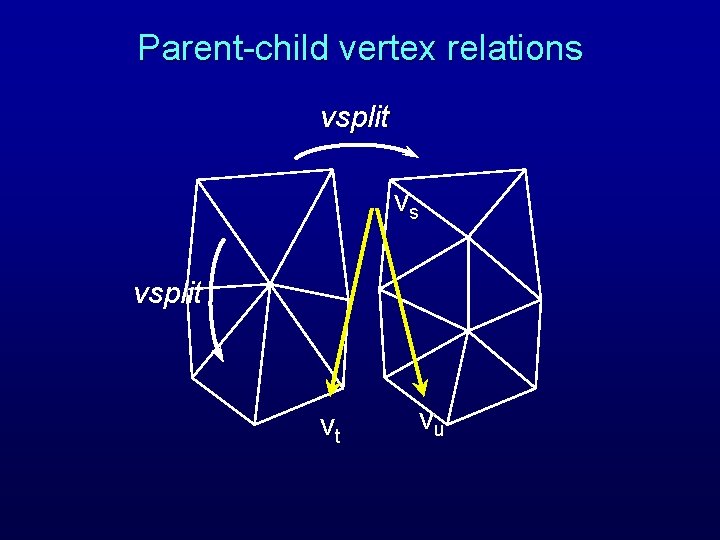
Parent-child vertex relations vsplit vt vu

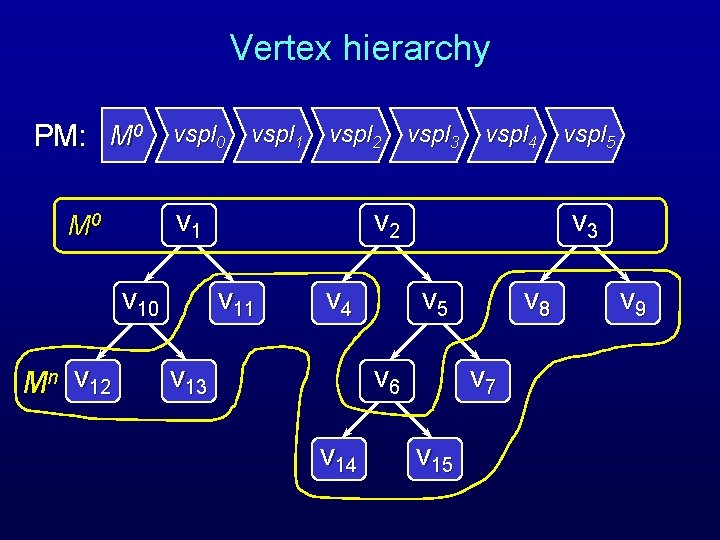
Vertex hierarchy PM: M 0 vspl 2 v 1 M 0 v 10 Mn v 12 vspl 1 vspl 3 vspl 4 v 2 v 11 v 4 v 13 v 5 v 6 v 14 vspl 5 v 8 v 7 v 15 v 9

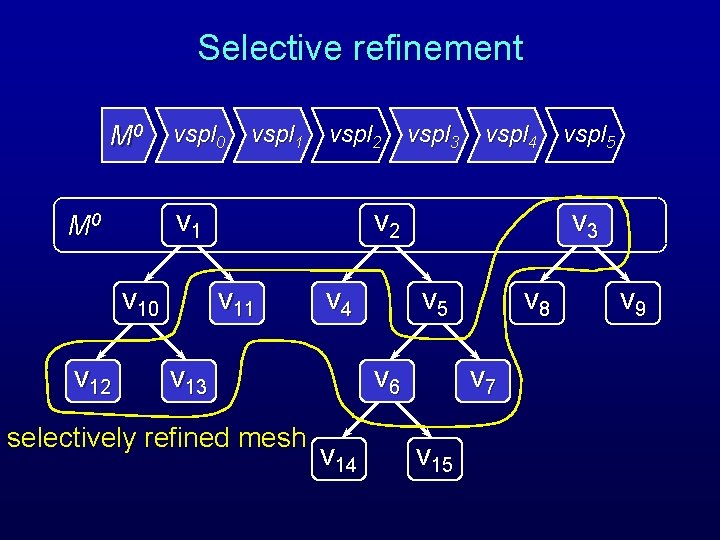
Selective refinement M 0 vspl 2 v 1 M 0 v 12 vspl 1 vspl 3 vspl 4 v 2 v 11 v 4 v 13 selectively refined mesh v 3 v 5 v 6 v 14 vspl 5 v 8 v 7 v 15 v 9

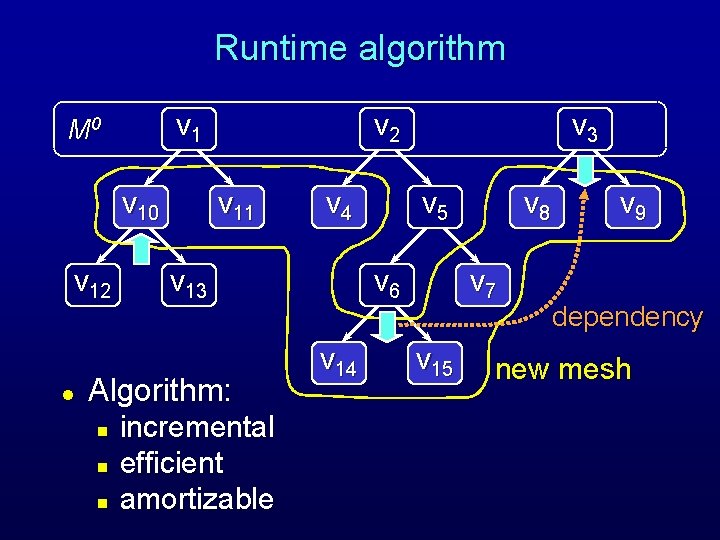
Runtime algorithm v 1 M 0 v 12 v 11 v 13 initial mesh l Algorithm: n n n v 4 incremental efficient amortizable v 3 v 5 v 6 v 14 v 8 v 7 v 15 v 9 dependency new mesh

DEMO: View-dependent LOD demo

Complex terrain model Puget Sound data 16 K x 16 K vertices ~537 million triangles 10 m spacing, 0. 1 m resolution 4 m demo simpler 10 m demo

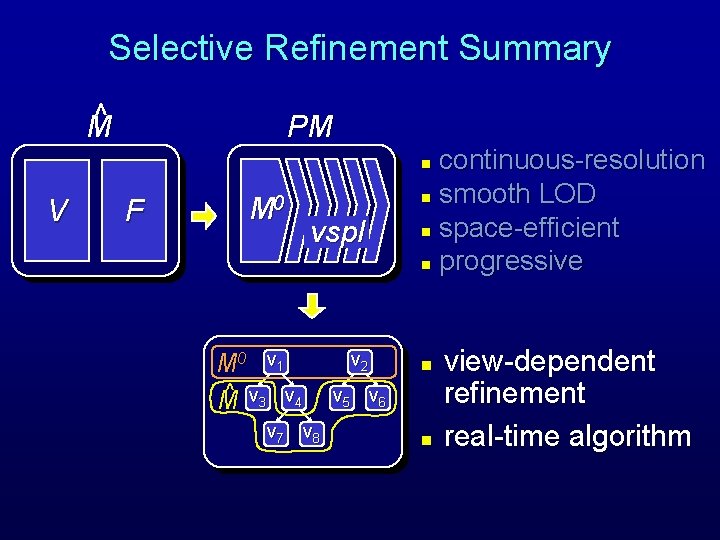
Selective Refinement Summary ^ M PM continuous-resolution n smooth LOD n space-efficient n progressive n V F M 0 vspl M 0 v 1 ^ v v M 3 4 v 7 v 8 v 2 n v 5 v 6 n view-dependent refinement real-time algorithm

Texture mapping progressive meshes l [Sander et al 2001] Construct texture atlas valid for all M 0…Mn. e. g. 1000 faces demo pre-shaded demo

Multiresolution geometry l Irregular meshes n n n l [1996] [1997] [2001] Semi-regular meshes n l Progressive meshes View-dependent refinement Texture-mapping PM Multiresolution analysis [1995] Completely regular meshes n Geometry images [2002]

Semi-regular representations [Eck et al 1995] [Lee et al 1998] [Khodakovsky 2000] [Guskov et al 2000] [Lee et al 2000] … irregular base mesh semi-regular

Challenge: finding domain [Eck et al 1995] [Lee et al 1998] [Khodakovsky 2000] [Guskov et al 2000] [Lee et al 2000] … base domain original surface

Techniques l “Delaunay” partition + parametrization [Eck et al. 1995] l Mesh simplification + … [Lee et al. 1998] [Lee et al. 2000] [Guskov et al. 2000]

Semi-regular: Applications l l l View-dependent refinement [Lounsbery et al. 1994] [Certain et al. 1995] Texture-mapping [Zorin et al. 1997] Multiresolution editing [Khodakovsky et al. 1999] Compression …

Multiresolution geometry l Irregular meshes n n n l [1996] [1997] [2001] Semi-regular meshes n l Progressive meshes View-dependent refinement Texture-mapping PM Multiresolution analysis [1995] Completely regular meshes n Geometry images [2002]

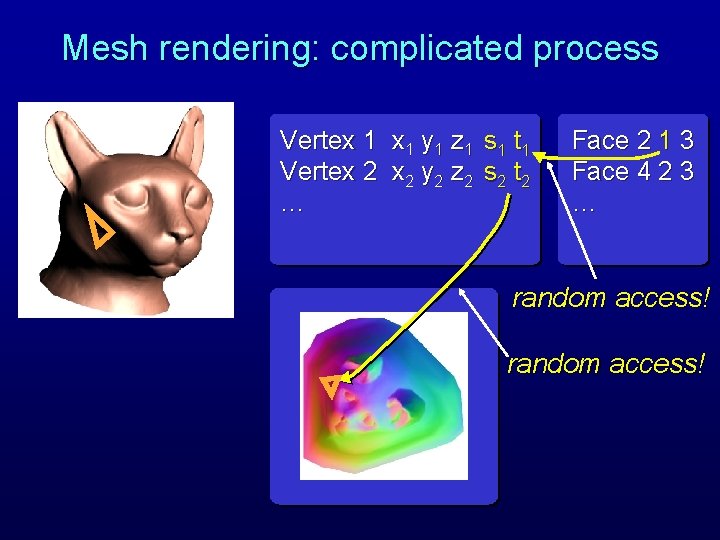
Mesh rendering: complicated process Vertex 1 y 1 z 1 s 1 t 1 Vertex 2 y 2 z 2 s 2 t 2 … Face 2 1 3 Face 4 2 3 … random access!

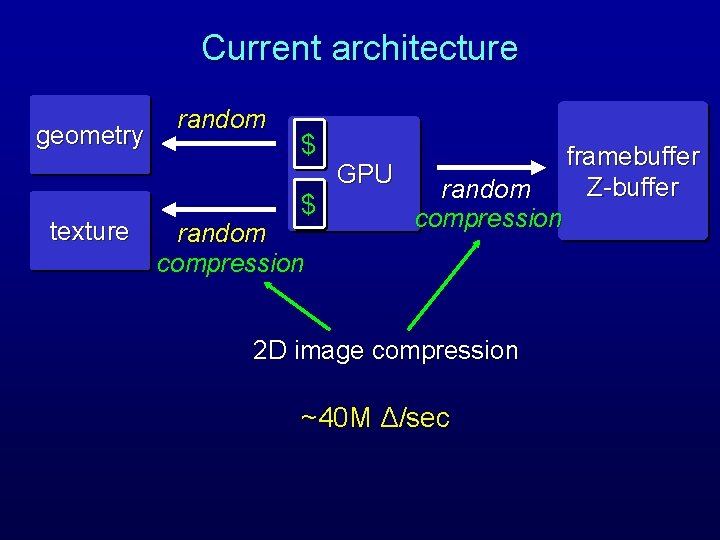
Current architecture geometry texture random $ $ random compression GPU random compression 2 D image compression ~40 M Δ/sec framebuffer Z-buffer

New architecture geometry sequential & texture GPU image great compression n n ~random compression framebuffer Z-buffer Minimize #vertices bandwidth, through compression. Maximize sequential (non-random) access

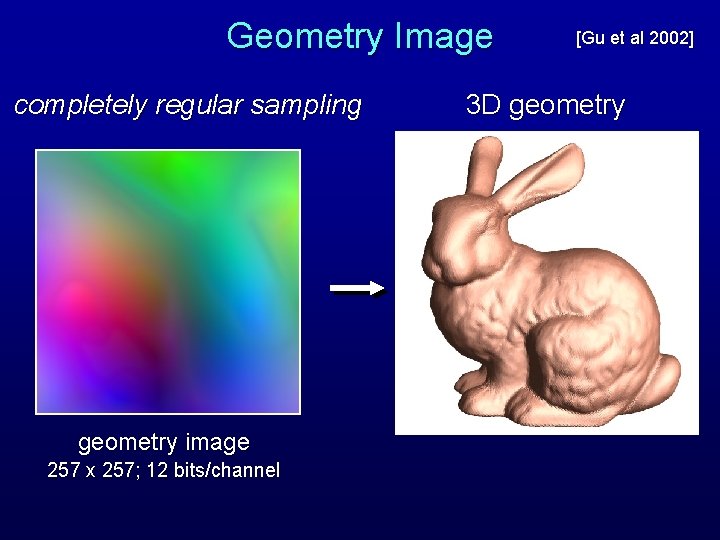
Geometry Image completely regular sampling geometry image 257 x 257; 12 bits/channel [Gu et al 2002] 3 D geometry

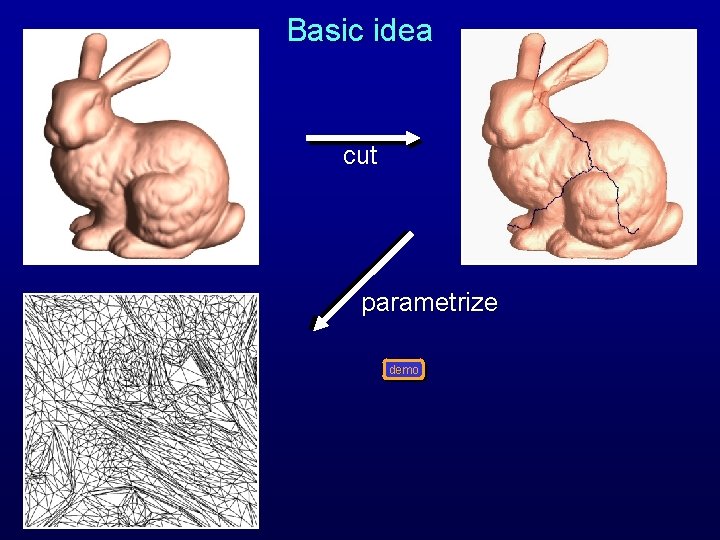
Basic idea cut parametrize demo

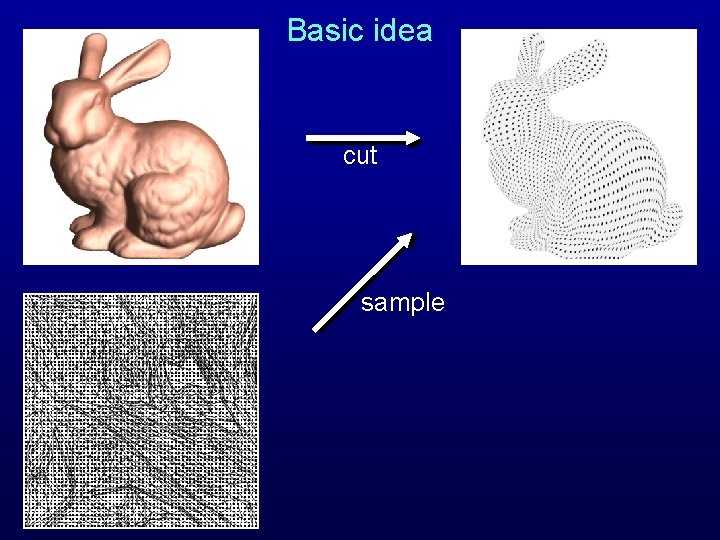
Basic idea cut sample

Basic idea cut store render [r, g, b] = [x, y, z]

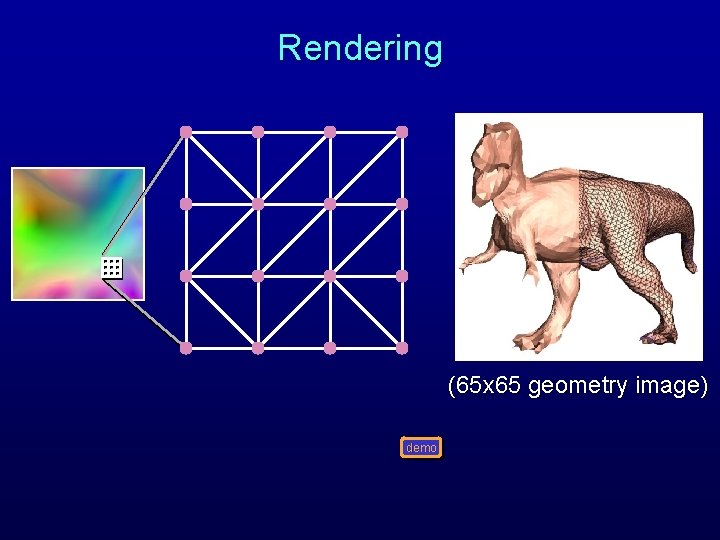
Rendering (65 x 65 geometry image) demo

Rendering with attributes geometry image 2572 x 12 b/ch normal-map image 5122 x 8 b/ch rendering

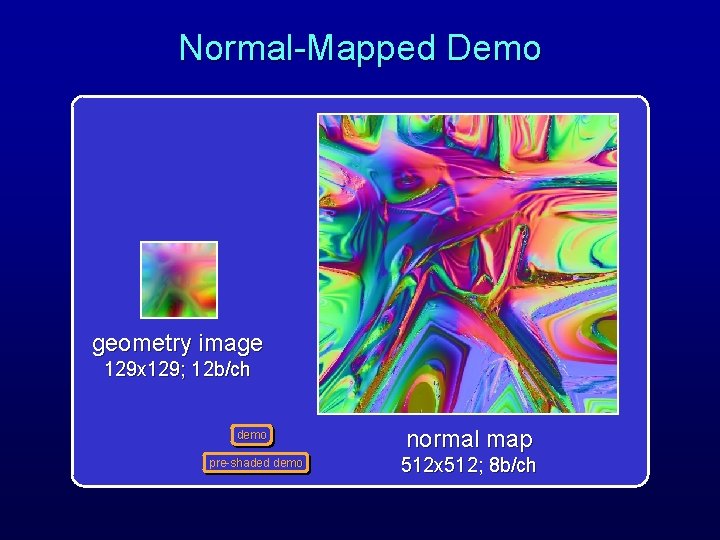
Normal-Mapped Demo geometry image 129 x 129; 12 b/ch demo pre-shaded demo normal map 512 x 512; 8 b/ch

Advantages for hardware rendering l Regular sampling no vertex indices. l Unified parametrization no texture coordinates. Raster-scan traversal of source data Run-time decompression?

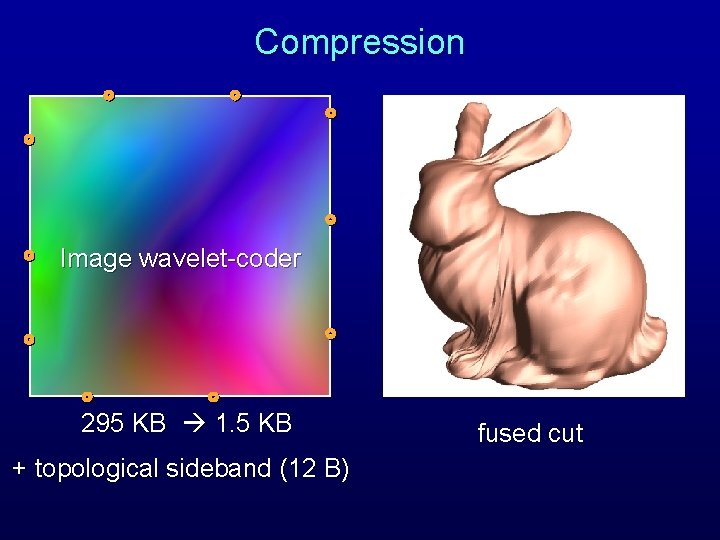
Compression Image wavelet-coder 295 KB 1. 5 KB + topological sideband (12 B) fused cut

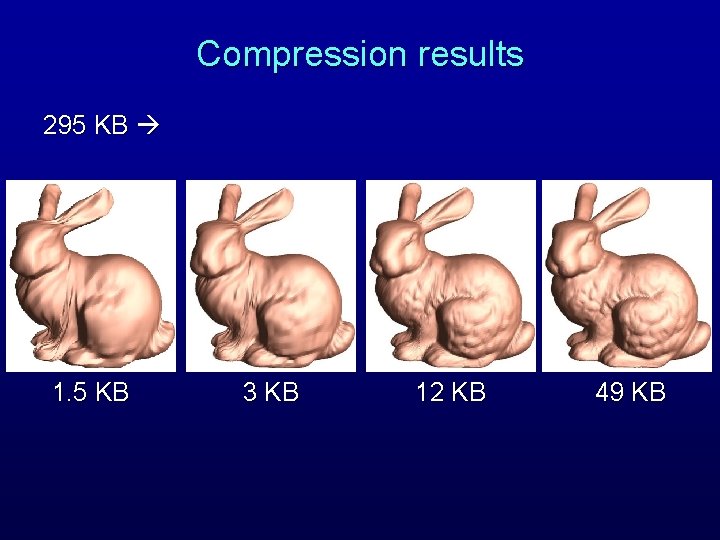
Compression results 295 KB 1. 5 KB 3 KB 12 KB 49 KB

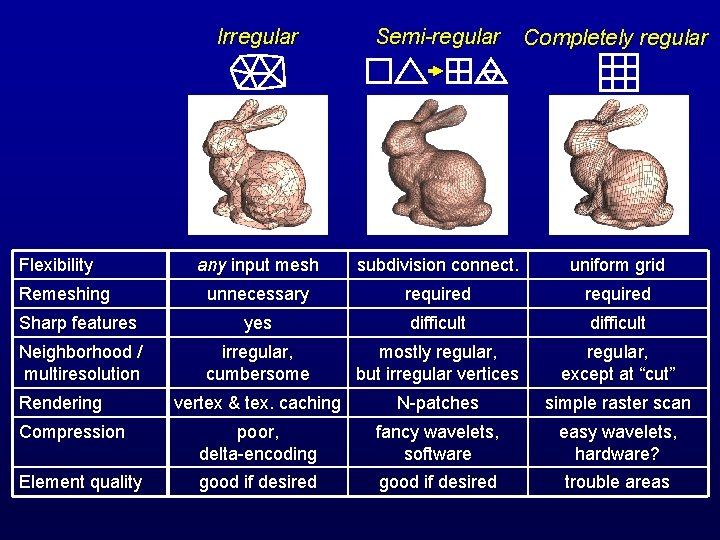
Irregular Semi-regular Completely regular any input mesh subdivision connect. uniform grid unnecessary required Sharp features yes difficult Neighborhood / multiresolution irregular, cumbersome mostly regular, but irregular vertices regular, except at “cut” vertex & tex. caching N-patches simple raster scan Compression poor, delta-encoding fancy wavelets, software easy wavelets, hardware? Element quality good if desired trouble areas Flexibility Remeshing Rendering

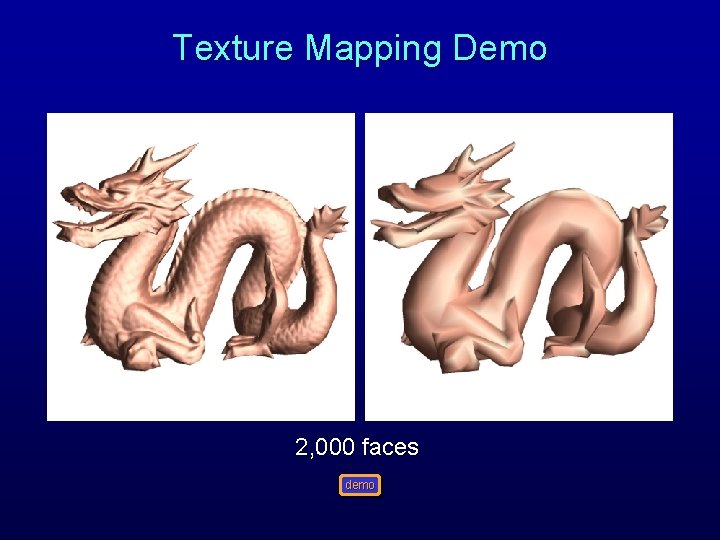
Texture Mapping Demo 2, 000 faces demo

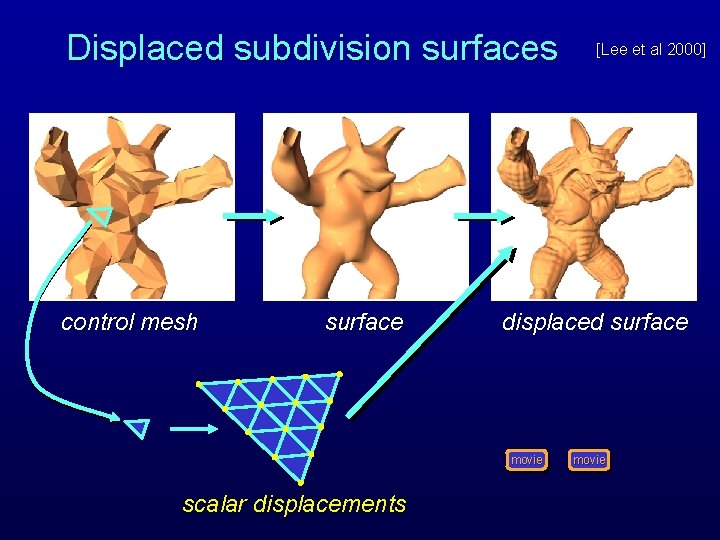
Displaced subdivision surfaces control mesh surface displaced surface movie scalar displacements [Lee et al 2000] movie

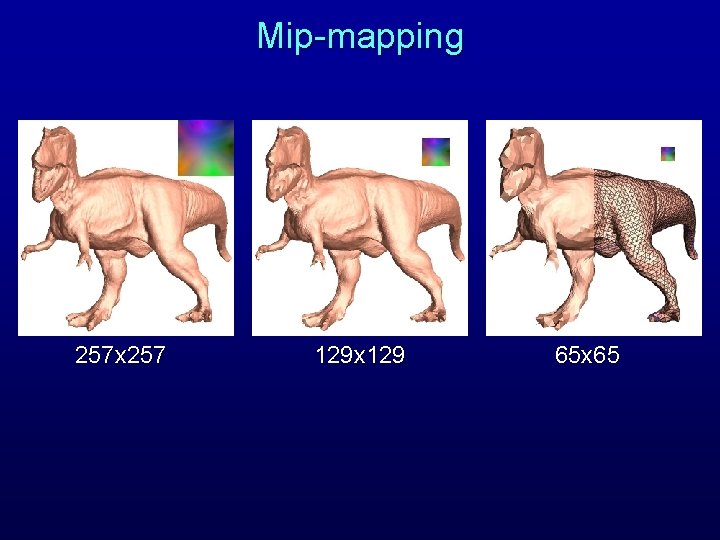
Mip-mapping 257 x 257 129 x 129 65 x 65

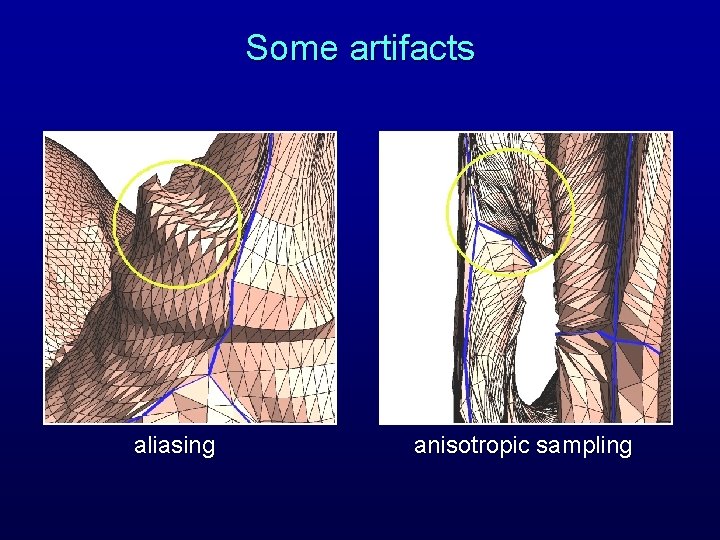
Some artifacts aliasing anisotropic sampling