IRRATIONAL NUMBERS When it came to measuring quantities

IRRATIONAL NUMBERS

• When it came to measuring quantities in dissimilar vessels, such a proportion could only be found by finding a unit of measure by which both vessels could be measured as a whole number Anthyphairesis

ANTHYPHAIRESIS • GO TO MATH HISTORY LESSON TO SEE PROCESS!!!!

INCOMMENSURABILITY • Egyptiona and Babylonians calculated square roots • These were approximated • Not appreciated • Hippasus of Metapontum • Credited for discovering Irrationals • Died for revealing the discovery

• First recorded proof that irrational is • Euclid’s Elements • Here is the most popular proof INCOMMESURABILITY

THE HISTORY OF PI Approximation of Pi • 1650 BC: Rhind Papyrus x = 3. 16045 • 950 BC Temple of Solomon: π = 3

THE HISTORY OF PI Approximation of Pi • 250 BC: Archimedes 3. 1418 • 150 CE: Ptolemy used a 360 – gon • 3. 14166 • 263 CE: Liu Hiu used a 192 regular inscribed polygon • 3. 14159 • 480 CE: Zu Chongzhi used a 24576 gon • 3. 141929265

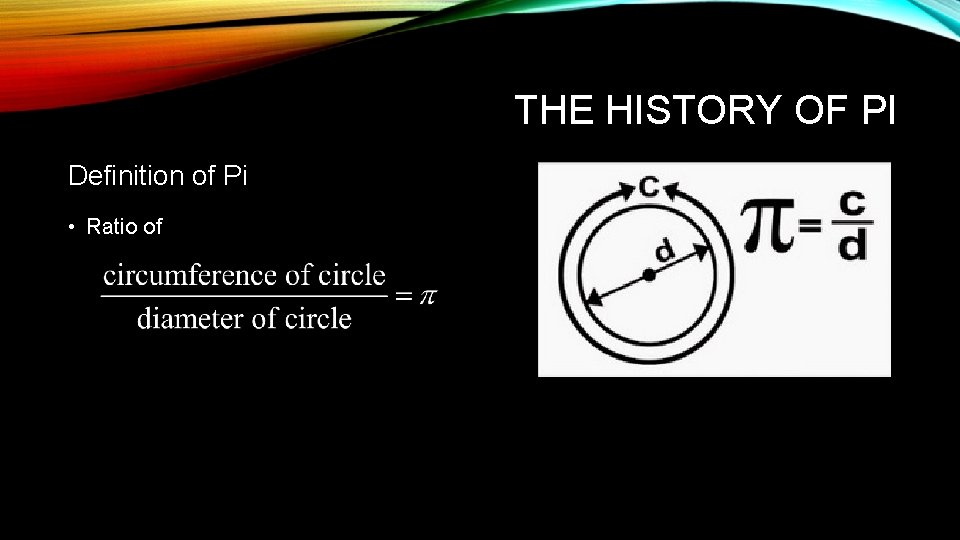
THE HISTORY OF PI Definition of Pi • Ratio of

1. Sometimes known as Euler’s constant. 2. The first references to “e” were in the appendix of a work by John Napier 3. The discovery of the constant itself is credited to Jacob Bernoulli THE HISTORY OF This is what Bernoulli was trying to solve when he discovered e

NEGATIVE NUMBERS

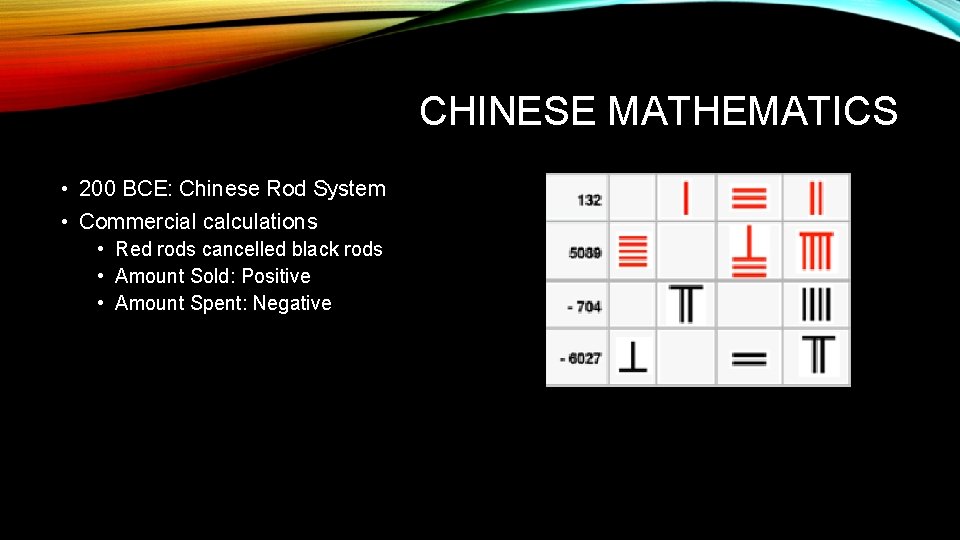
CHINESE MATHEMATICS • 200 BCE: Chinese Rod System • Commercial calculations • Red rods cancelled black rods • Amount Sold: Positive • Amount Spent: Negative

NEGATIVE NUMBERS IN INDIA • Brahmagupta – 7 th Century Mathematician • 1 st wrote of negative numbers • Zero already had a value • Developed rules for negative numbers • Developed the Integers we know

ARITHMETIC RULES WITH INTEGERS Brahmagupta’s work Translation to modern day • A debt minus zero is a debt • Negative – 0 = negative • A fortune minus zero is a fortune • Positive – 0 = positive • Zero minus zero is zero • 0– 0=0 • A debt subtracted from zero is a fortune • 0 – negative = positive • A fortune subtracted from zero is a debt • 0 – positive = negative

Brahmagupta’s work 1. 2. 3. 4. 5. 6. ARITHMETIC RULES WITH INTEGERS – CONT’D A product of zero multiplied by a debt or fortune is zero The product of zero multiplied by zero is zero The product or quotient of two fortunes is a fortune The product or quotient of two debts is a fortune The product or quotient of a debt and a fortune is a debt The product or quotient of a fortune and a debt is a debt

NEGATIVE NUMBERS IN GREECE Ignored and Neglected by Greeks • 300 CE: Diophantus wrote Arithmetica • 4 = 4 x + 20 • “Absurd result” Why would problems arising from Geometry cause Greeks to ignore negative numbers?

ARABIAN MATHEMATICS Also ignored negatives • Al-Khwarizami’s Algebra book – • • 780 CE Acknowledged Brahmagupta Heaviily influenced by the Greeks Called Negative Results “meaningless”

ARABIAN MATHEMATICS – CONT’D Al-Samaw’al (1130 – 1180 CE) • Shining Book of Calculations • Produced statements regarding algebra • Had no difficulty handling negative expressions His contribution to math al-Samawal is said to have been developing algebra of polynomials He introduced decimals, well before its appearance in Europe

AL-SAMAWAL’S ALGEBRA • If we subtract a positive number from an ‘empty power’, the same negative number remains. • If we subtract the negative number from an ‘empty power’, the same positive number remains. • The product of a negative number by a positive number is negative, and be a negative number is positive.

EUROPEAN MATHEMATICS • 15 th century • Arabs brought negatives to Europe • Translated ancient Islamic and Byzantine texts • Spurred solutions to quadratics and cubics

EUROPEAN MATHEMATICS • Luca Pacioli (1445 – 1517) • Summa de arithmetica, geometria • Double Entry Book-Keeping • He kept the use of negatives alive • John Wallis ( 1616 -1703) • English • Invented Number Line

EUROPEAN MATHEMATICS • 1758: Francis Maseres • British “ (negative numbers) darken the very whole doctrines of the equations and made dark the things which are in their nature excessively obvious and simple”

EUROPEAN MATHEMATICS • 1770: Euler • Swiss “Since negative numbers may be considered as debts. . . We say that negative numbers are less than nothing. Thus, when a man has nothing of his own, and owes 50 crowns, it is certain that he has 50 crowns less than nothing; though if any were to make a present of 50 crowns to pay his debt, he would still have nothing, though really richer than before. ”

POTENTIAL INFINITY VS ACTUAL INFINITY

SOURCES History of Negative Numbers: http: //nrich. maths. org/5961 https: //brilliant. org/discussions/thread/discovery-of-irrational-numbers/ https: //www. math. rutgers. edu/~cherlin/History/Papers 2000/wilson. html Mac. Tutor History of Mathematics: http: //www-history. mcs. st-and. ac. uk