IRISAN KERUCUT Oleh Neng Siva Afni N 0704318

IRISAN KERUCUT Oleh Neng Siva Afni N (0704318) Iis Ismayani (070434)

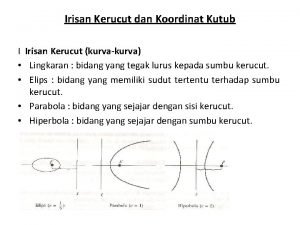
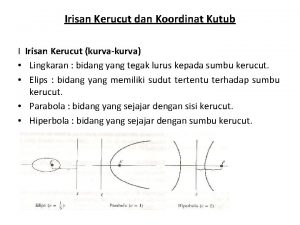
Pengertian Himpunan titik (x, y) yang memenuhi persamaan AX 2 + BXY + CY 2 + DX + EY + F = 0 disebut irisan kerucut. Secara geometris kurvanya dapat diperoleh dengan memotong suatu kerucut tegak lurus dengan suatu bidang datar.

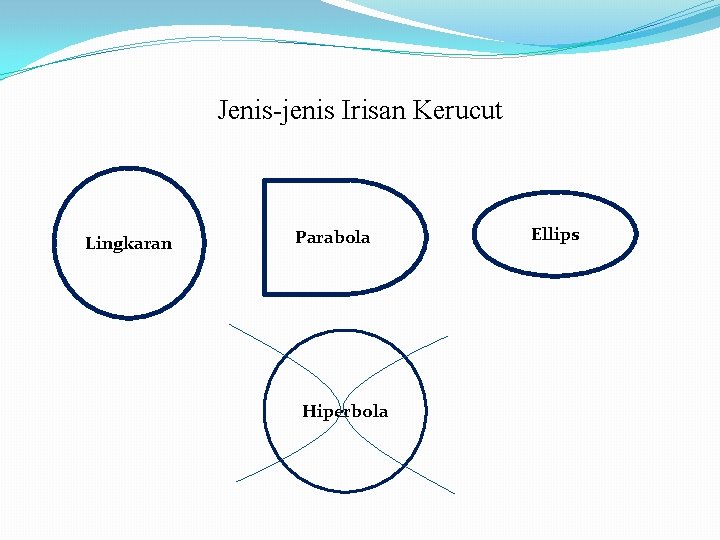
Jenis-jenis Irisan Kerucut Lingkaran Parabola Hiperbola Ellips

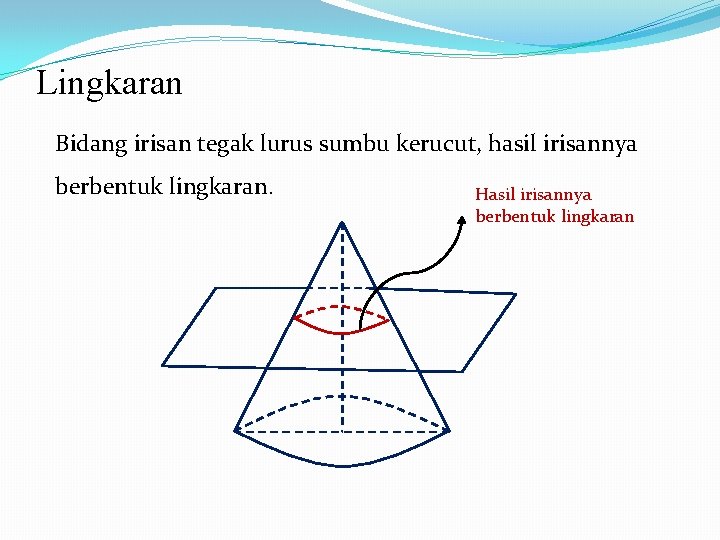
Lingkaran Bidang irisan tegak lurus sumbu kerucut, hasil irisannya berbentuk lingkaran. Hasil irisannya berbentuk lingkaran

�Definisi Lingkaran adalah tempat kedudukan titik-titik yang berjarak sama terhadap suatu titik tertentu. Titik tertentu itu disebut pusat lingkaran. Y jari-jari (r) merupakan jarak titik pusat lingkaran terhadap lingkaran. P(x, y) r O X

Persamaan Lingkaran a. Persamaan Lingkaran dengan pusat di (0, 0) Y Perhatikan gambar disamping! Jarak dari titik P(x, y) ke pusat lingkaran (0, 0) adalah: PO = P(x, y) r O <=> r = X <=> r 2 = Jadi, persamaan lingkaran dengan pusat di (0, 0) adalah: r 2 =

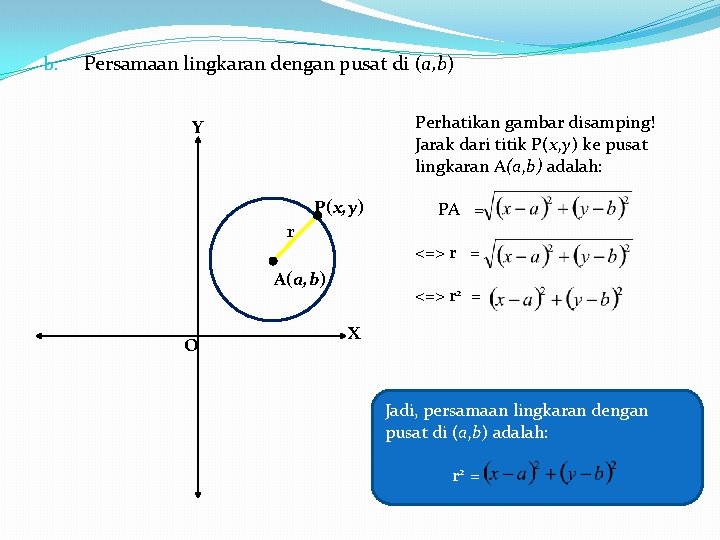
b. Persamaan lingkaran dengan pusat di (a, b) Perhatikan gambar disamping! Jarak dari titik P(x, y) ke pusat lingkaran A(a, b) adalah: Y P(x, y) r <=> r = A(a, b) O PA = <=> r 2 = X Jadi, persamaan lingkaran dengan pusat di (a, b) adalah: r 2 =

Contoh Soal Buktikan bahwa adalah persamaan lingkaran dan kemudian tentukan pusat dan jari-jarinya. Jawab: <=> <=> <=> Jadi, terbukti bahwa persamaan lingkaran dengan pusat (-1, 4) dan jari-jari 5 adalah persamaan

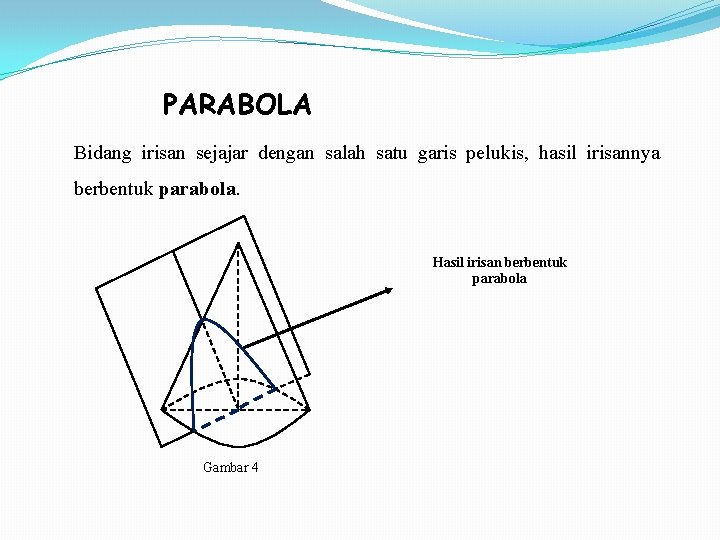
PARABOLA Bidang irisan sejajar dengan salah satu garis pelukis, hasil irisannya berbentuk parabola. Hasil irisan berbentuk parabola Gambar 4

Definisi Parabola: Parabola adalah tempat kedudukan titik-titik P sedemikian sehingga jarak P dari suatu titik tertentu selalu sama jaraknya dari suatu garis tertentu. Y A P(x, y) O X F(P, 0) A’ x = -p Gambar 5

Titik tertentu itu disebut fokus, garis tertentu itu disebut direktriks. Garis yang tegak lurus pada direktriks dan melalui fokus disebut sumbu parabola. Perpotongan antara sumbu dan parabola disebut puncak parabola. Untuk memperoleh persamaan parabola, ambil sumbu-sumbu koordinat yang fokus F mempunyai koordinat F(p, 0) dan garis direktriks AA’ mempunyai persamaan x = -p, dan puncak parabola (0, 0). (lihat gambar 5) Pengambilan sumbu-sumbu koordinat itu menuju ke persamaan yang paling sederhana. Menurut definisi, jarak PF harus sama dengan jarak dari P ke AA’ (tegak lurus).

Jarak P ke AA’ adalah Jarak P ke F adalah Sehingga diperoleh: . . . (kedua ruas dikuadratkan) Jadi, persamaan parabola dengan fokus F(p, 0) dan garis direktriks x= -p adalah

Dengan cara yang sama dapat diperoleh persamaan-persamaan parabola dengan fokus dan direktriks yang berbeda. Persamaan-persamaan parabola tersebut dapat disajikan dalam tabel berikut. q Puncak (0, 0) Persamaa n Fokus Direktri ks Sumbu parabola Grafiknya (p, 0) x = -p Sumbu x Terbuka ke kanan (-p, 0) x =p Sumbu x Terbuka ke kiri (0, p) y = -p Sumbu y Terbuka ke atas (0, -p) y=p Sumbu y Terbuka ke bawah

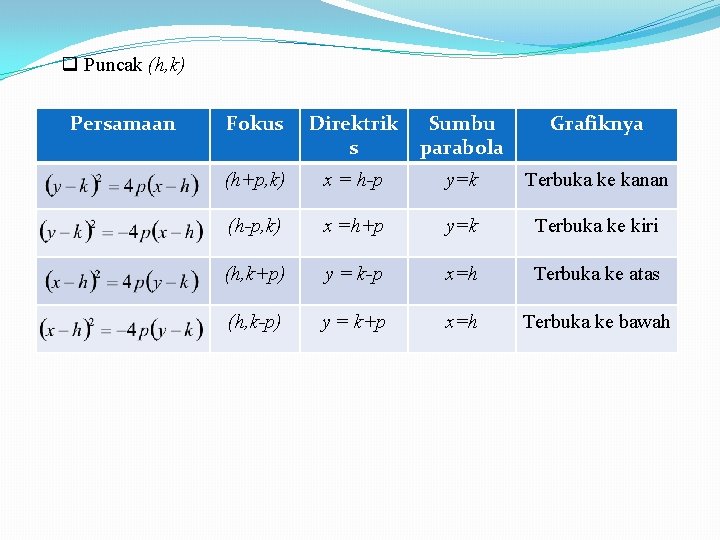
q Puncak (h, k) Persamaan Fokus Direktrik s Sumbu parabola Grafiknya (h+p, k) x = h-p y=k Terbuka ke kanan (h-p, k) x =h+p y=k Terbuka ke kiri (h, k+p) y = k-p x=h Terbuka ke atas (h, k-p) y = k+p x=h Terbuka ke bawah

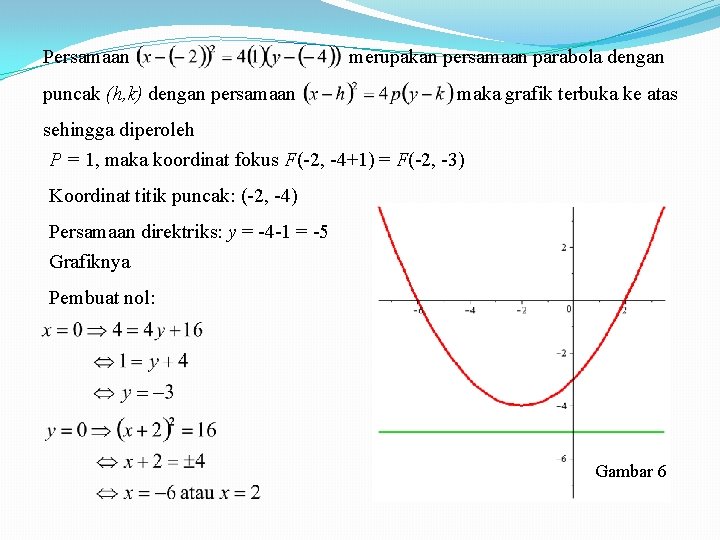
Contoh: Tentukan koordinat fokus, koordinat titik puncak, persamaan direktriks, dan lukiskan grafiknya dari parabola dengan persamaan Jawab: Persamaan di atas diubah menjadi bentuk umum persamaan parabola, diperoleh

Persamaan puncak (h, k) dengan persamaan merupakan persamaan parabola dengan maka grafik terbuka ke atas sehingga diperoleh P = 1, maka koordinat fokus F(-2, -4+1) = F(-2, -3) Koordinat titik puncak: (-2, -4) Persamaan direktriks: y = -4 -1 = -5 Grafiknya Pembuat nol: Gambar 6

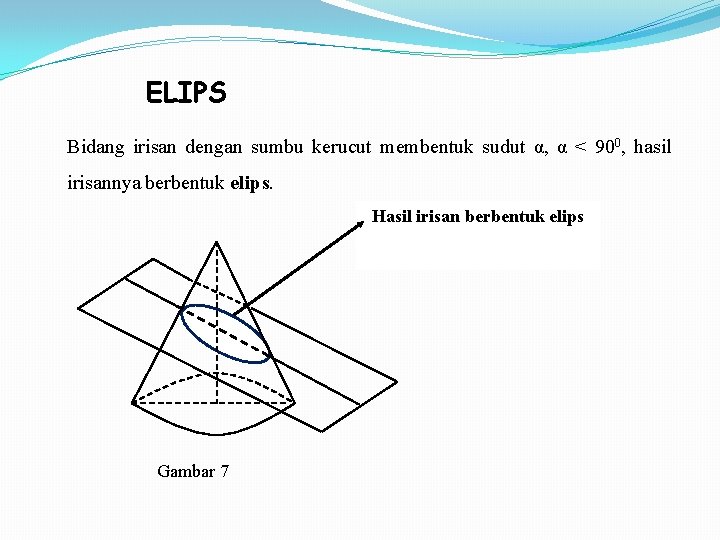
ELIPS Bidang irisan dengan sumbu kerucut membentuk sudut α, α < 900, hasil irisannya berbentuk elips. Hasil irisan berbentuk elips Gambar 7

Definisi Elips: Elips adalah tempat kedudukan titik-titik P sedemikian sehingga jumlah jarak P terhadap dua titik tertentu adalah tetap. Y D(0, b) b A(-a, 0) F 1(-p, 0) P(x, y) a F 2(p, 0) O p B(0, -b) Gambar 8 C(a, 0) X

§ Kedua titik tertentu itu disebut fokus-fokus elips. § Garis penghubung kedua fokus disebut sumbu panjang (sumbu mayor). § Garis melalui titik tengah kedua fokus dan tegak lurus terhadap sumbu mayor disebut sumbu pendek (sumbu minor). § Titik potong kedua sumbu disebut pusat elips. § Titik potong elips dengan kedua sumbu disebut puncak elips (A, B, C, D). § Jarak A ke C dan B ke D masing-masing merupakan panjang dari sumbu panjang dan sumbu pendek. Persamaan elips dapat diperoleh dengan: § Pilih sumbu-sumbu yang berfokus § Misalkan jumlah jarak yang tetap adalah 2 a berarti 2 a > 2 p atau a > p

Sehingga menurut definisi, diperoleh Kuadratkan kedua ruas, maka diperoleh

Kuadratkan kembali kedua ruas, maka diperoleh Karena a > p, maka Misalkan Maka persamaan (1) menjadi

Bagilah masing-masing ruas persamaan (2) dengan Jadi, persamaan elips dengan fokus , maka diperoleh adalah

Dengan cara yang sama dapat diperoleh persamaan-persamaan elips dengan fokus, sumbu mayor dan sumbu minor yang berbeda. Persamaan-persamaan elips tersebut dapat disajikan dalam tabel berikut. q Pusat (0, 0) Persamaan Fokus Sumbu mayor Sumbu minor Terletak pada sumbu x Terletak pada sumbu y Terletak pada sumbu x

q Pusat (h, k) Persamaan Fokus Sumbu mayor Sumbu minor y=k x=h x= h y=k

Contoh: Diketahui elips dengan persamaan Tentukanlah: a) Koordinat titik pusat elips b) Panjang sumbu mayor dan panjang sumbu minor c) Koordinat fokus-fokus d) Koordinat titik-titik puncak e) Lukiskan grafiknya

Jawab: Persamaan di atas diubah menjadi bentuk umum persamaan elips, diperoleh Dari persamaan (*), dapat ditentukan a) Koordinat titik pusat elips: (2, 1)

b) Menghitung panjang sumbu mayor dan sumbu minor Panjang sumbu mayor = 2 a = 2 x 10 =20 Panjang sumbu minor = 2 b = 2 x 5 = 10 c) Mencari koordinat fokus Koordinat fokus-fokus:

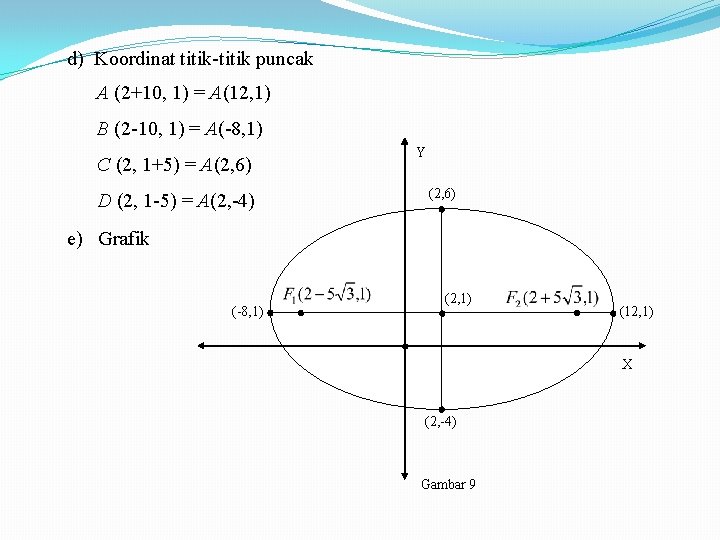
d) Koordinat titik-titik puncak A (2+10, 1) = A(12, 1) B (2 -10, 1) = A(-8, 1) C (2, 1+5) = A(2, 6) D (2, 1 -5) = A(2, -4) Y (2, 6) e) Grafik (-8, 1) (2, 1) (12, 1) X (2, -4) Gambar 9

HIPERBOLA Bidang irisan sejajar dengan sumbu kerucut hasil irisannya berbentuk hiperbola Hasil irisannya berbentuk hiperbola

Definisi Hiperbola