Investment Analysis and Portfolio Management Lecture 5 Gareth

Investment Analysis and Portfolio Management Lecture 5 Gareth Myles

Risk l l l An investment is made at time 0 The return is realised at time 1 Only in very special circumstances is the return to be obtained at time 1 known at time 0 In general the return is risky The choice of portfolio must be made taking this risk into account The concept of states of the world can be used

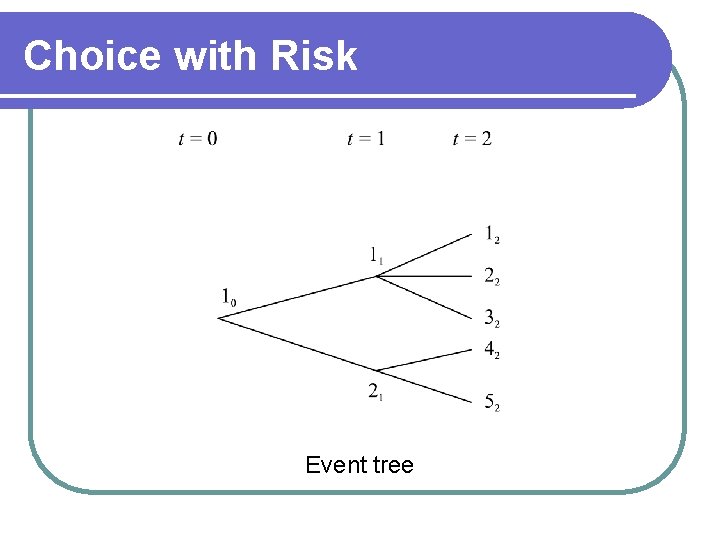
Choice with Risk l State Preference l The standard analysis of choice in risky situations applies the state preference approach Consider time periods t = 1, 2, 3, 4, . . . l At each time t there is a set of possible events (or "states of the world") l

Choice with Risk When time t is reached, one of these states is realized l At the decision point (t = 0), it is not known which l Decision maker places a probability on each event l The probabilities satisfy l

Choice with Risk Event tree

Choice with Risk Each event is a complete description of the world l Let = return on asset i at time t in state e then l This information will determine the payoff in each state l Investors have preferences over these returns and this determines preferences over states l

Choice with Risk l Expected Utility l Assume the investor has preferences over wealth in each state described by the utility function l Preferences can be defined over different sets of probabilities over the states

Choice with Risk Assume 1 time period and 2 states l Let wealth in state 1 be W 1 and in state 2 W 2 l Let p denote the lottery {p, 1 -p} in which state 1 occurs with probability p l Lottery q is defined in the same way l Example l Let , , , l Then any investor who prefers a higher return to a lower return must rank p strictly preferable to q

Choice with Risk l We now assume that an investor can rank lotteries l l 1. Preferences are a complete ordering 2. If p is preferred to q, then a mixture of p and r is preferred to the same mixture of r and q 3. If p is preferred to q and q preferred to r, then there is a mixture of p and r which is preferred to q and a different mixture of p and r which is strictly worse then q The investor will act as if they maximize the expected utility function

Choice with Risk This approach can be extended to the general state-preference model described above l For example, with two assets in each state l where ai is the investment in asset i l Summary l Preferences over random payoffs can be described by the expected utility function

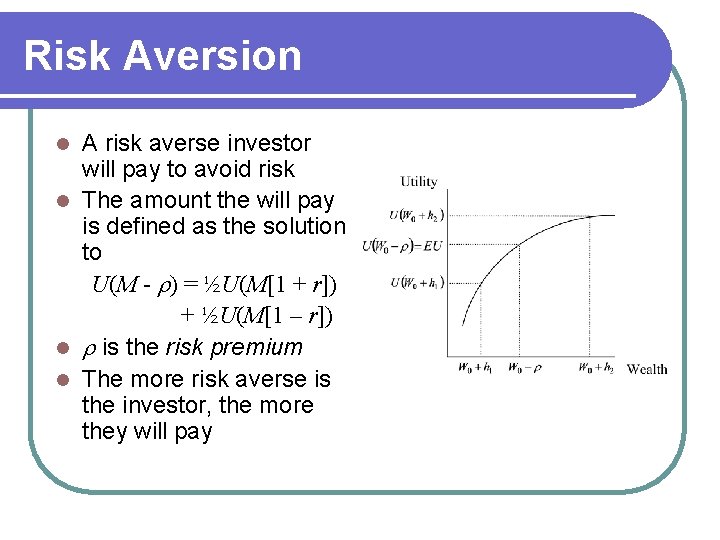
Risk Aversion Consider receiving either l l l A fixed income M A random income M[1 + r] or M[1 – r], each possibility occurring with probability ½ An investor is risk averse if U(M) > ½ U(M[1 + r]) + ½ U(M[1 – r]) The certain income is preferred to the random income This holds if the utility function is concave

Risk Aversion A risk averse investor will pay to avoid risk l The amount the will pay is defined as the solution to U(M - r) = ½U(M[1 + r]) + ½U(M[1 – r]) l r is the risk premium l The more risk averse is the investor, the more they will pay l

Portfolio Choice Assume a safe asset with return rf = 0 l Assume a risky asset l l l Return rg > 0 in “good” state Return rb < 0 in “bad” state Investor has amount W to invest l How should it be allocated between the assets? l

Portfolio Choice Let amount a be placed in risky asset, so W – a in safe asset l After one period l l l Wealth is W - a + a[1 + rg] in good state Wealth is W - a + a[1 + rb] in bad state A portfolio choice is a value of a l High value of a l l l More wealth if good state occurs Less wealth if bad states occurs

Portfolio Choice l Possible wealth levels are illustrated on a “state-preference” diagram Wealth in bad state a=0 W a=W W[1+rb] W W[1+rg] Wealth in good state

Portfolio Choice Adding indifference curves shows the choice l Indifference curves from expected utility function EU = p. U(W - a + a[1 + rg]) + (1 -p)U(W - a + a[1 + rb]) l The investor chooses a to make expected utility as large as possible l Attains the highest indifference curve given the wealth to be invested l

Portfolio Choice Wealth in bad state W a=0 a* W[1+rb] a=W W W[1+rg] Wealth in good state

Portfolio Choice l l l Effect of an increase in risk aversion What happens if rb > 0 or if rg < 0? When will some of the risky asset be purchased? When will only safe asset be purchased? Effect of an increase in wealth to be invested?

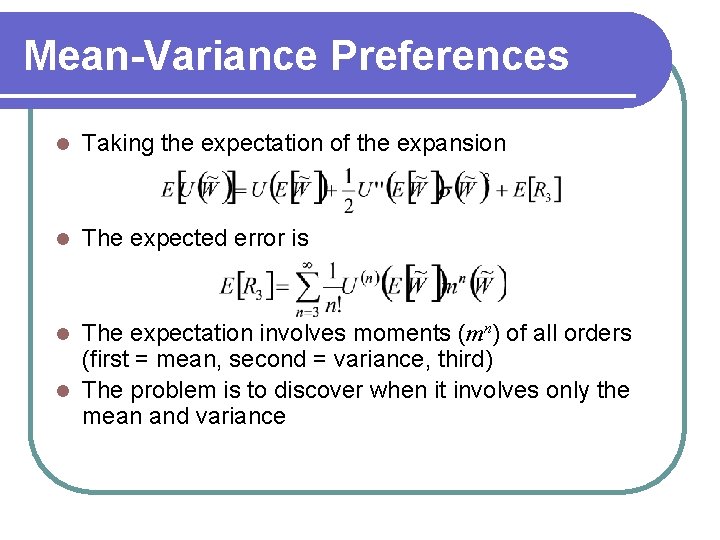
Mean-Variance Preferences There is a special case of this analysis that is of great significance in finance l The general expected utility function constructed above is dependent upon the entire distribution of returns l The analysis is much simpler if it depends on only the mean and variance of the distribution. l When does this hold? l

Mean-Variance Preferences l Denote the level of wealth by. Taking a Taylor's series expansion of utility around expected wealth l Here R 3 is the error that depends on terms involving and higher

Mean-Variance Preferences l Taking the expectation of the expansion l The expected error is The expectation involves moments (mn) of all orders (first = mean, second = variance, third) l The problem is to discover when it involves only the mean and variance l

Mean-Variance Preferences l Expected utility depends on just the mean and variance if either l l = 0 for n > 2. This holds if utility is Or l l 1. quadratic 2. The distribution of returns is normal since then all moments depend on the mean and variance In either case

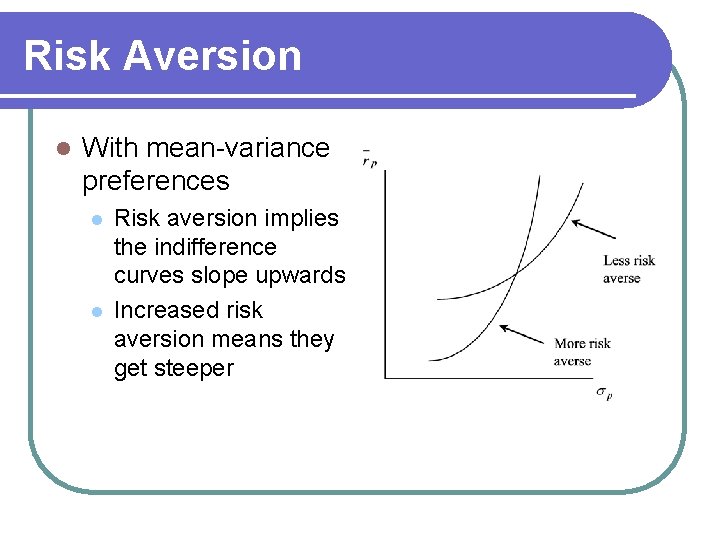
Risk Aversion l With mean-variance preferences l l Risk aversion implies the indifference curves slope upwards Increased risk aversion means they get steeper

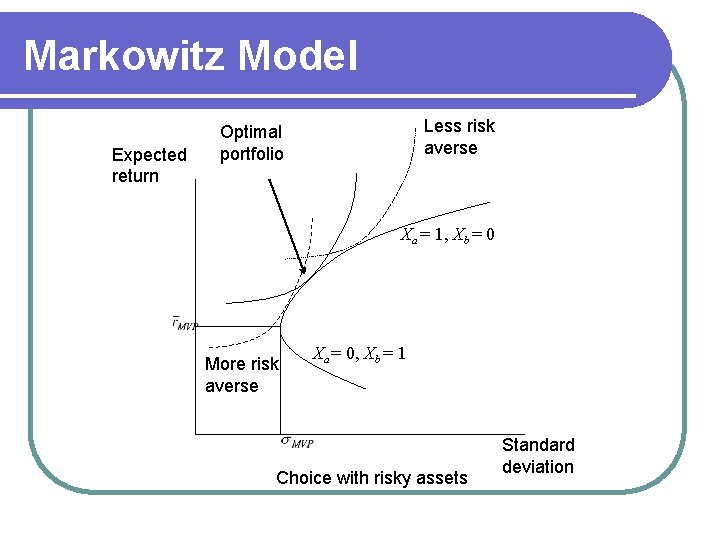
Markowitz Model The Markowitz model is the basic model of portfolio choice l Assumes l l l A single period horizon Mean-variance preferences Risk aversion Investor can construct portfolio frontier

Markowitz Model Confront the portfolio frontier with meanvariance preference l Optimal portfolio is on the highest indifference curve l An increase in risk aversion changes the gradient of the indifference curve l Moves choice around the frontier l

Markowitz Model Expected return Less risk averse Optimal portfolio Xa = 1, Xb = 0 More risk averse Xa = 0, Xb = 1 Choice with risky assets Standard deviation

Markowitz Model Expected return Optimal portfolio Less risk averse Borrowing Xa = 1, Xb = 0 More risk averse Lending Xa = 0, Xb = 1 Choice with a risk-free asset Standard deviation

Markowitz Model Note the role of the tangency portfolio l Only two assets need be available to achieve an optimal portfolio l l Model makes predictions about l l Riskfree asset Tangency portfolio (mutual fund) The effect of an increase in risk aversion Which assets will be short sold Which investors will buy on the margin Markowitz model is the basis of CAPM