Investigation Find the distance between two points A1

Investigation. Find the distance between two points A(1, 2) and B(3, 6) x-length = 3 – 1 = 2 • • B(3, 6) 6 (6 – 2 ) Form a triangle and use Pythagoras to find the distance between the points 4 2 2 • • A(1, 2) y-length = 6 – 2 = 4 Length = √(22 + 42 = √ 20 • 1 (3 – 1 ) • 3

Co-ordinate Geometry Chapter 7

Note 1 : Distance between two points Let A (x 1 , y 1) and B (x 2 , y 2) be two points. A (x 1 , y 1) D B (x 2 , y 2) y 2 – y 1 x 2 – x 1 We often need to find d, the distance between A and B. This is found using PYTHAGORAS

Example: Find the distance between the points (– 3, 2) and (3, -6) (x 1, y 1) substitute into the formula d = 10 units (x 2, y 2)

Applications Prove that the vertices A(1, 5), B(2, 9) and C(6, 10) are those of an isosceles triangle. AB = √ 17 BC = √ 17 AC = √ 50 Because there is two sides with the same length the triangle is isosceles.

Theata Page 128 Exercise 16. 2

Investigation Consider the two numbers 6 and 10. The number exactly halfway between them, their MIDPOINT, is 8. The midpoint can easily be worked out by counting inwards from 6 and 10, but you can also find the midpoint by averaging the two numbers. This averaging is a really useful process when the numbers are not as easy to work with as 6 and 10
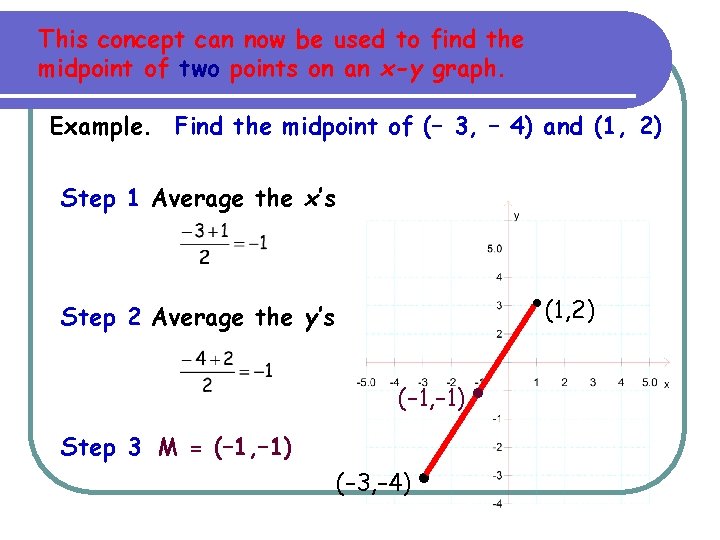
This concept can now be used to find the midpoint of two points on an x-y graph. Example. Find the midpoint of (– 3, – 4) and (1, 2) Step 1 Average the x’s • (1, 2) Step 2 Average the y’s (– 1, – 1) Step 3 M = (– 1, – 1) (– 3, – 4) • •
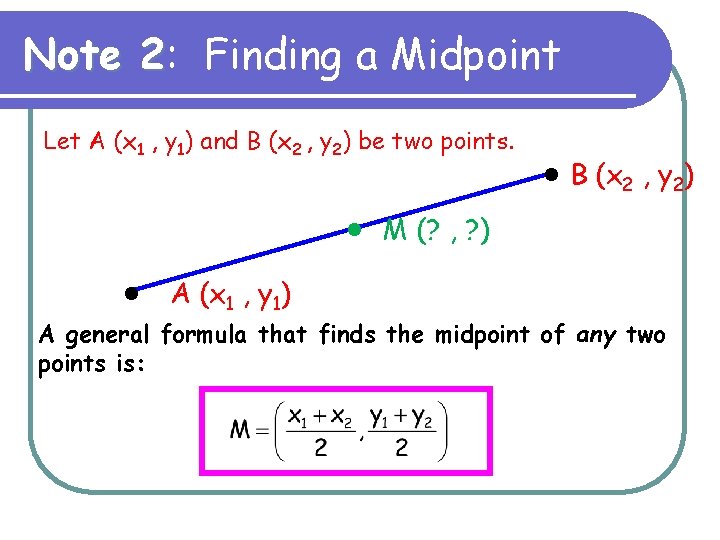
Note 2: 2 Finding a Midpoint Let A (x 1 , y 1) and B (x 2 , y 2) be two points. A (x 1 , y 1) B (x 2 , y 2) M (? , ? ) A general formula that finds the midpoint of any two points is:

Example: Find the midpoint of the line segment joining E = (10, -3) and F = (6, 0) (6 , 0) (x 1 , y 1) (10, -3) (x M = (8, -1. 5) 2 , y 2)

Prove that the points A(-1, -2), B(1, 1), C(8, -1) and D(6, -4) are the vertices of a parallelogram. (HINT: find the lengths of all four sides and the diagonals) AB = 3. 6 units BC = 7. 3 units DC = 3. 6 units AD = 7. 3 units AC = 9. 1 units BD = 7. 1 units Length of AB = length of CD and length of BC = length of AD. The lengths of the diagonals are different, so therefore the shape is a parallelogram

Theata Page 127 Exercise 16. 1

Starter Find the midpoints of the line segments joining (6, -2) and (1, 2) midpoint = (3½, 0) (3, -2) and (1, -6) midpoint = (2, -4)
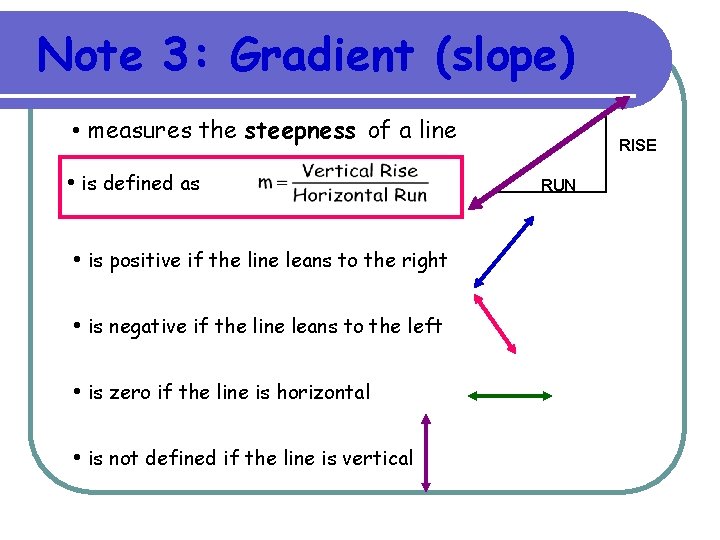
Note 3: Gradient (slope) • measures the steepness of a line • is defined as • is positive if the line leans to the right • is negative if the line leans to the left • is zero if the line is horizontal • is not defined if the line is vertical RISE RUN
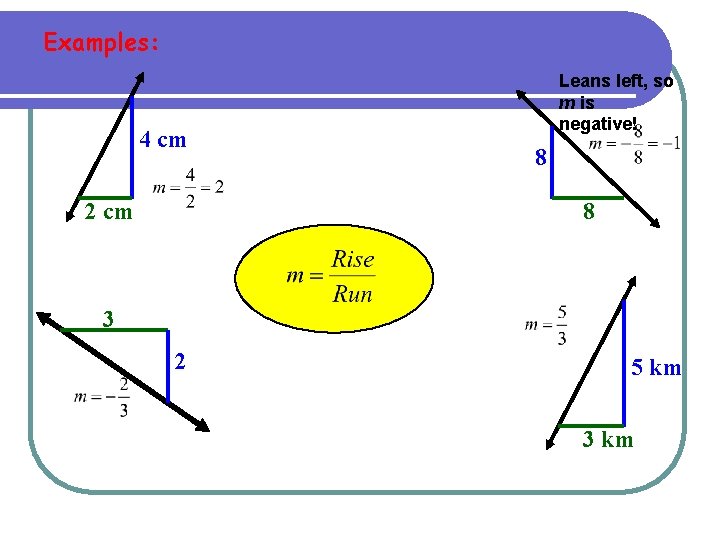
Examples: 4 cm 2 cm Leans left, so m is negative! 8 8 3 2 5 km 3 km
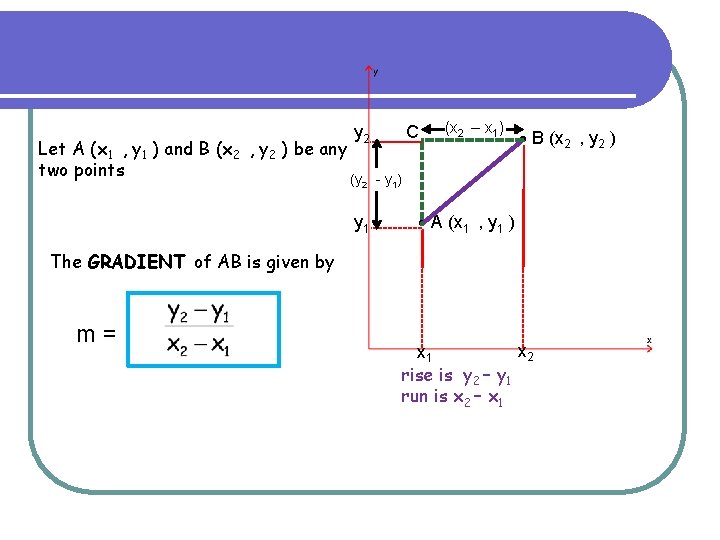
C y 2 Let A (x 1 , y 1 ) and B (x 2 , y 2 ) be any two points (y 2 y 1 (x 2 – x 1) B (x 2 , y 2 ) - y 1) A (x 1 , y 1 ) The GRADIENT of AB is given by m= x 2 x 1 rise is y 2 – y 1 run is x 2 – x 1
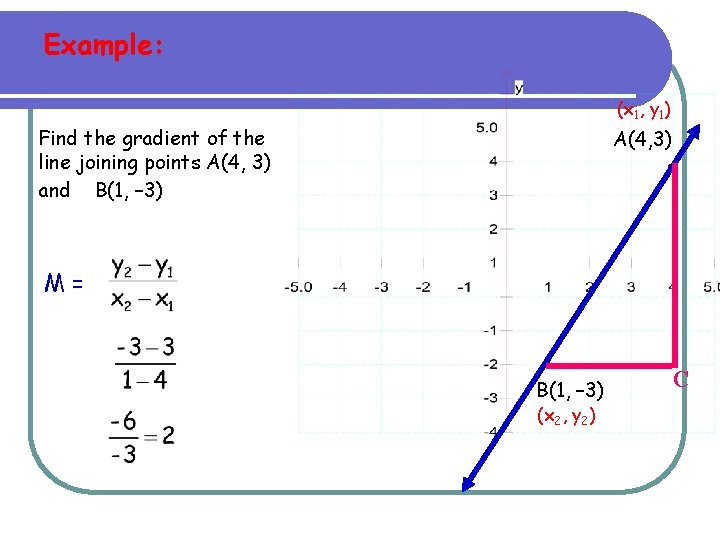
Example: (x 1, y 1) Find the gradient of the line joining points A(4, 3) and B(1, – 3) A(4, 3) • M= • B(1, – 3) (x 2, y 2) C

Parallel and Perpendicular lines Parallel lines have the same gradient Perpendicular lines gradients are the negative reciprocals of each other m 1 x m 2 = -1 Example: If line AB has a gradient of 2/3, and line CD is perpendicular to line AB, what is the gradient of CD? Gradient of CD = -3/2 Points are collinear if they lie on the same line – their gradients are equal
Page 137 Exercise 7 A

Note 4: Revision of Equations of Lines The gradient/intercept form for the equation of a line is: y = mx + c gradient y-intercept

Example: Plot y = -2/3 x + 2 using the gradient and intercept method y-intercept (c) = 2 Gradient (m) = -2 3 Fall is 2 Run is 3 Negative sign means it leans to LEFT ü Plot the y-intercept ü Plot the next point by making a triangle, whose fall is 2 and run is 3 ü Plot another point in the same manner ü Connect the points with a straight line
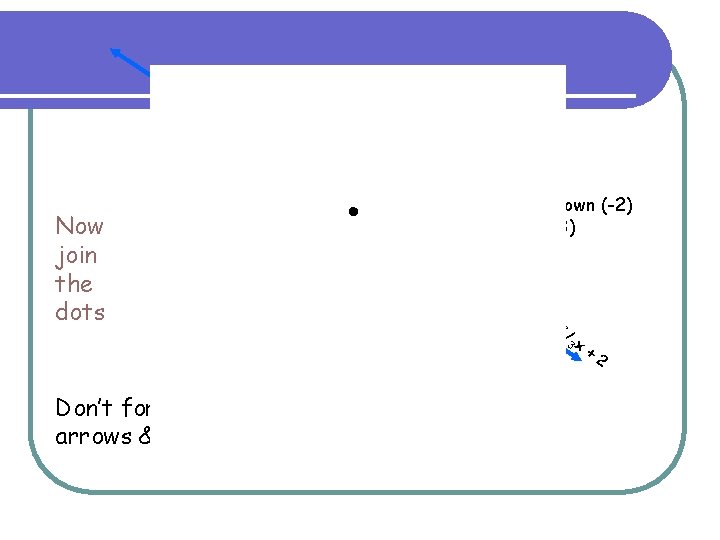
Another option: up (+2) then left (-3) Now join the dots One option: down (-2) then right (+3) y= - 2/ 3 x Don’t forget arrows & label +2

Exercises: Plot the following graphs; y = 2 x – 3 Y = -⅖x + 2 y=x

The general form of the equation of a line is: ax + by + c = 0 Equations can be rearranged from gradientintercept form to the general form by performing operations on both sides of the equation. (a is usually positive)

Example: Write the following equation in the general form y = -2/3 x + 2 3 y = -2 x + 6 2 x + 3 y – 6 = 0 Multiply equation by 3 Move everything to the LHS

Exercises: Write the following equations in the general form: y = 4 x – 3 4 x – y - 3 = 0 Y = -⅖x + 2 2 x + 5 y - 10 = 0 y = ⅙x – ⅚ x - 6 y - 5 = 0

Note 5: Finding Equations of Lines If you know • the gradient, m and • any point, (x 1 , y 1) then the equation of the line can be worked out using the formula y – y 1 = m (x – x 1)

Example 1 Find the equation of the line passing through (– 3, 5) and with gradient 4 Step 1 Write m, x 1 and y 1 m = 4 x 1 = – 3 y 1 = 5 Step 2 Put these values into the formula Step 3 y – y 1 = m(x – x 1) y – 5 = 4(x – – 3) Remove brackets. Write in general form y – 5 = 4(x + 3) y = 4 x + 17 y – 5 = 4 x + 12 0 = 4 x - y + 17

Example 2 Find the equation of the line passing through (– 2, -13) and (3, 2) Step 1 Find m m = Step 2 (x 1, y 1) (x 2, y 2) =3 Put these values into the formula y – y 1 = m(x – x 1) Step 3 y – -13 = 3(x – – 2) Remove brackets. Write in general form Y + 13 = 3(x + 2) y = 3 x - 7 Y + 13 = 3 x + 6 0 = 3 x - y - 7

Note 5 a: Finding Equations of Lines Quickly For slope the form of the line is Ax – By = … For slope the form of the line is Ax + By = … Example: Find the equation of the line which passes through (2, -5) with a gradient of ⅜ The equation is: 3 x – 8 y = 3(2) – 8(-5) 3 x – 8 y = 46

Exercise 7 B and C

Starter A car club has an annual hill climb competition. A cross section of part of the hill they race on is drawn below. The beginning and end points of the section, in metres from the start of the hill are given as co-ordinate pairs.

Find: § The gradient over this section of the hill climb m = 1/ 5 § What is the distance of this section of the hill climb in metres to the nearest metre? 153 m § What are the co-ordinates of the half-way point of this section of the hill climb? (215, 85)

STARTERS: Graph the following lines: 4 x + 12 y = 24 y = - 2/ 3 x + 4
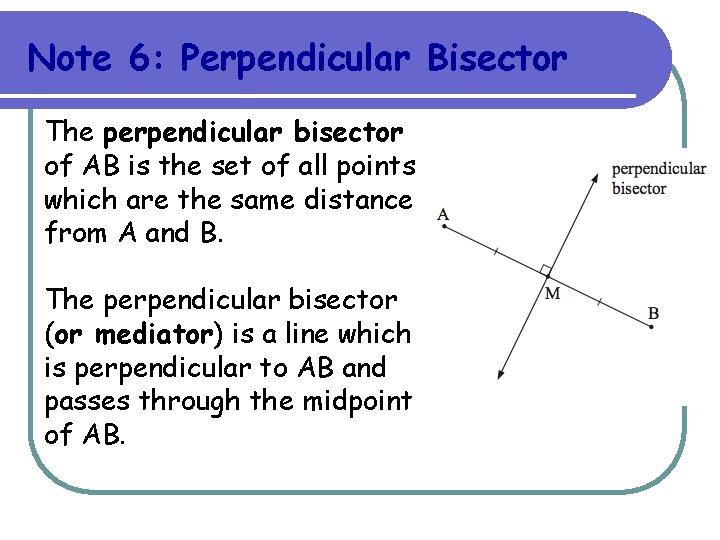
Note 6: Perpendicular Bisector The perpendicular bisector of AB is the set of all points which are the same distance from A and B. The perpendicular bisector (or mediator) is a line which is perpendicular to AB and passes through the midpoint of AB.

Example: Find the equation of the perpendicular bisector between the points A(-2, 5) and B(4, 9) Find the midpoint of AB: Find the gradient of AB: M = (1, 7) =⅔ The perpendicular gradient of AB = - 3/2 Equation of perpendicular bisector: y – 7 = - 3/2 (x – 1) 2 y – 14 = - 3 (x - 1) 2 y – 14 = - 3 x + 3 3 x + 2 y – 17 = 0

Page 146 Exercise 7 D. 1 and 7 D. 2
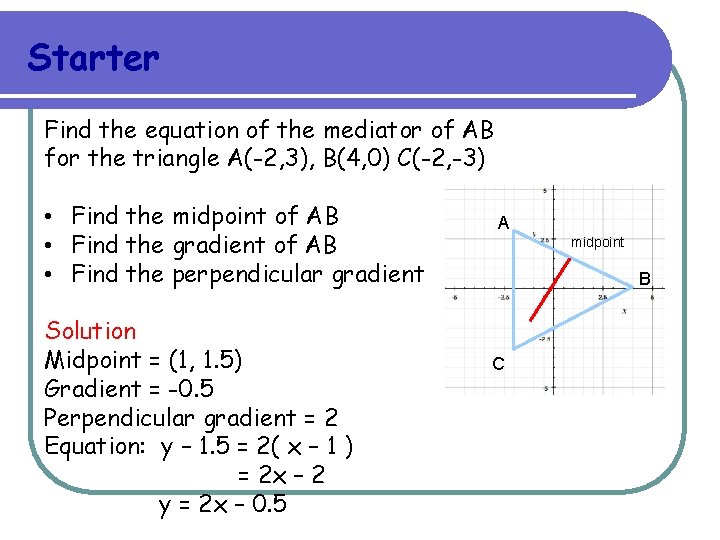
Starter Find the equation of the mediator of AB for the triangle A(-2, 3), B(4, 0) C(-2, -3) • Find the midpoint of AB • Find the gradient of AB • Find the perpendicular gradient Solution Midpoint = (1, 1. 5) Gradient = -0. 5 Perpendicular gradient = 2 Equation: y – 1. 5 = 2( x – 1 ) = 2 x – 2 y = 2 x – 0. 5 A midpoint B C

Starter 3 darts are thrown at a dart board. The first land in the bulls eye, the 2 nd lands 2 cm to the left and 1 cm above the bulls eye, the 3 rd lands 2 cm to the right and 9 cm above the bulls eye. • Calculate the distance between the points of the 2 nd and 3 rd darts • The equation of the line joining these two darts • Find the intersection of this line with its perpendicular bisector • Find the equation on this perpendicular bisector

Other Geometrical Terms • Equidistant – find the midpoint • Bisects – cuts into two equal parts • Perpendicular – at right angles • Vertex – corner of angle • Concurrent – pass through the same point • Collinear – lies on the same line

Note 7: Triangles – Altitude of Triangles The perpendicular distance from a vertex to the opposite side of a triangle is called the altitude (or height) Example: In the triangle A(-4, 4), B(2, 2) and C(-2, -1), calculate the length of the altitude of the triangle ABC through vertex C. Find the intersection of CI and AB • Find equation of CI • Solve a and b simultaneously
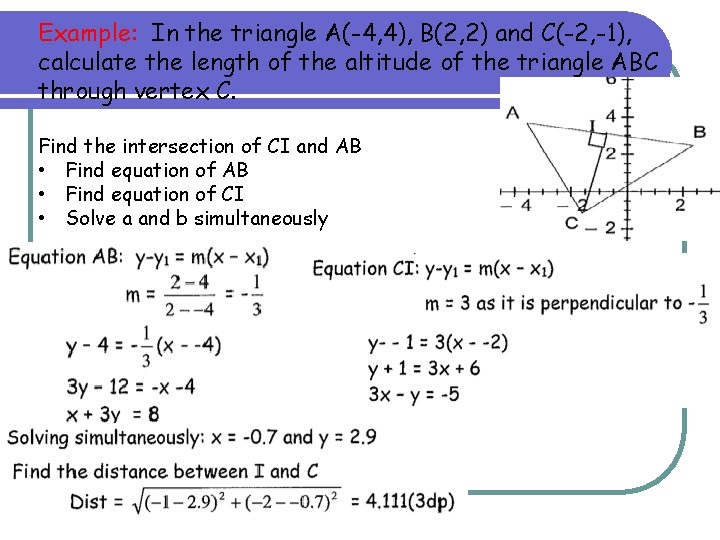
Example: In the triangle A(-4, 4), B(2, 2) and C(-2, -1), calculate the length of the altitude of the triangle ABC through vertex C. Find the intersection of CI and AB • Find equation of CI • Solve a and b simultaneously

Note 7: Triangles – Medians of Triangles A line drawn from a vertex of a triangle to a midpoint of the opposite side is called the median

Note 7: Triangles – Medians of Triangles
- Slides: 44