Investigating Cosmic Ray Muons Image source http ssg

Investigating Cosmic Ray Muons Image source: http: //ssg. sheffield. ac. uk 2015/07/03 COSMIC RAY-BANS

The Standard Model and Muons

The Standard Model and Muons μ-+

The Experiment • Cosmic Rays § High energy radiation, mostly protons § Secondary cosmic rays on impact with atmosphere → Cosmic ray muons

The Experiment • Scintillation • Both the entry and the decay of low energy muons are detected

Interpreting the Results

Further Investigation • Readily detectable Image source: https: //en. wikipedia. org

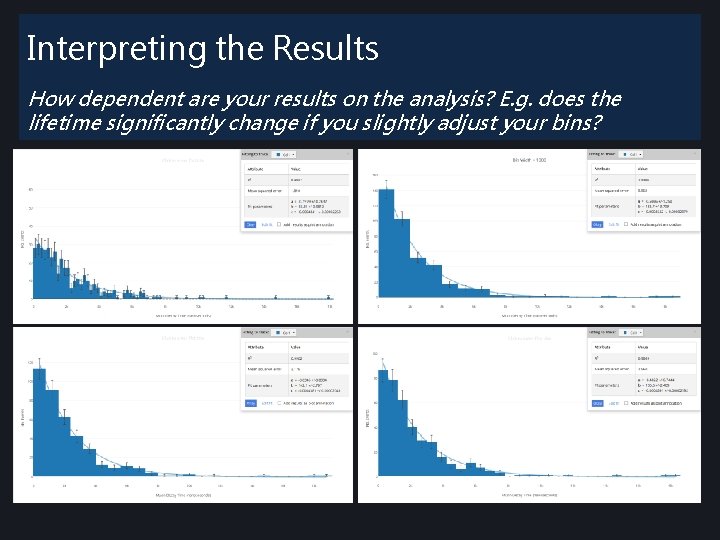
Interpreting the Results Second Data Set • Larger data set of 2000 to compare it with original data set 300

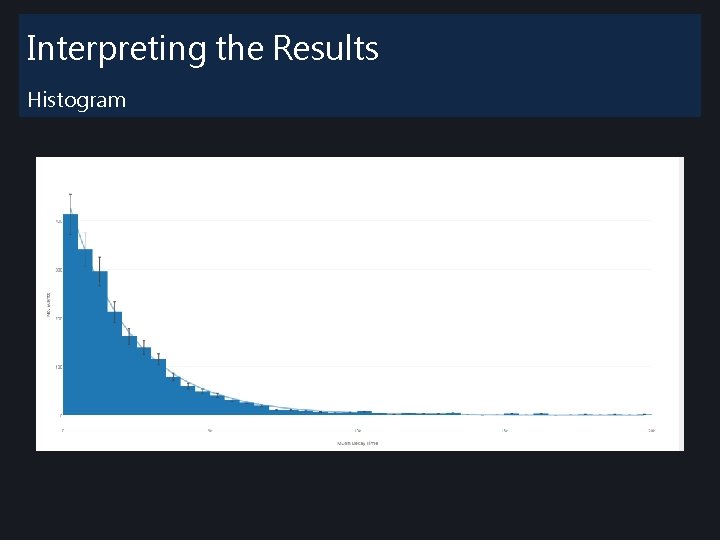
Interpreting the Results Histogram

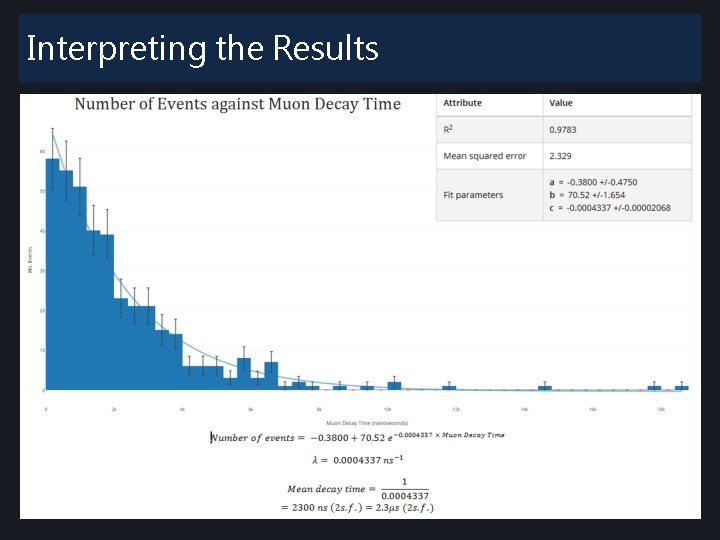
Interpreting the Results Calculations Number of events= -0. 3800+70. 52 e-0. 0004337 × Muon Decay Time λ= 0. 0004337 ns-1 Mean decay time= 10. 0004337 =2300 ns 2 s. f. =2. 3 ± 0. 10μs (2 s. f. )

Interpreting the Results Is your value of the mean lifetime of muons consistent (to within errors) of the current published value? If not, then why? Muon lifetime: 2. 1969811± 0. 0000022µs Initial calculated value: 2. 3μs • differs slightly from the published value of 2. 2μs • Small sample size, errors in the calculated line of best fit • Differences in experimental conditions vacuum • Detail lost - bin width • The more extensive data set gave results consistent with the published value.

Interpreting the Results How dependent are your results on the analysis? E. g. does the lifetime significantly change if you slightly adjust your bins?

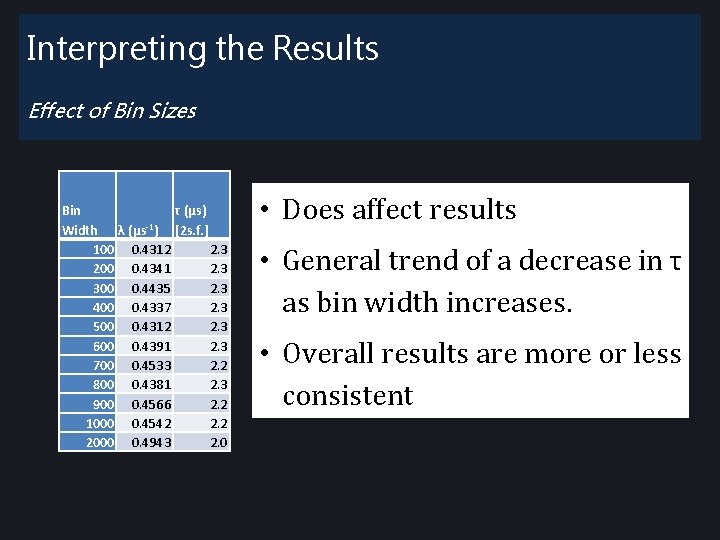
Interpreting the Results Effect of Bin Sizes Bin τ (μs) Width λ (μs-1) [2 s. f. ] 100 0. 4312 2. 3 200 0. 4341 2. 3 300 0. 4435 2. 3 400 0. 4337 2. 3 500 0. 4312 2. 3 600 0. 4391 2. 3 700 0. 4533 2. 2 800 0. 4381 2. 3 900 0. 4566 2. 2 1000 0. 4542 2. 2 2000 0. 4943 2. 0 • Does affect results • General trend of a decrease in τ as bin width increases. • Overall results are more or less consistent

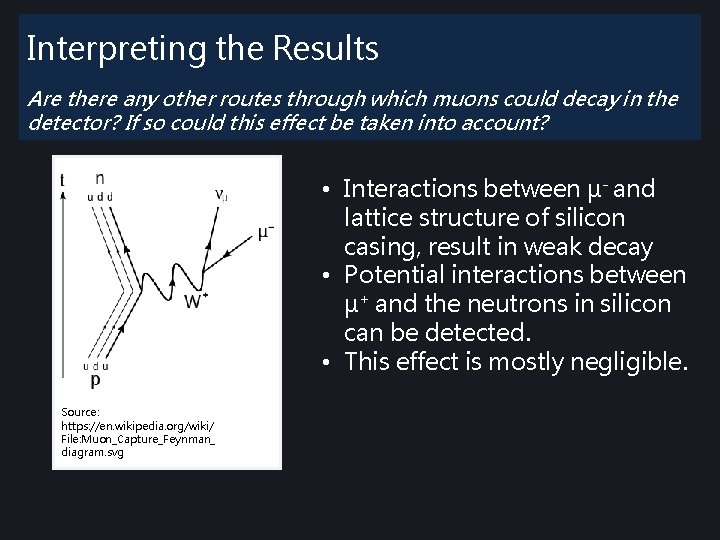
Interpreting the Results Are there any other routes through which muons could decay in the detector? If so could this effect be taken into account? • Interactions between μ- and lattice structure of silicon casing, result in weak decay • Potential interactions between μ+ and the neutrons in silicon can be detected. • This effect is mostly negligible. Source: https: //en. wikipedia. org/wiki/ File: Muon_Capture_Feynman_ diagram. svg

Interpreting the Results Are there any other ways an event could register in the detector not due to a single muon decay? What is the likelihood of this? • Two muons enter the scintillator simultaneously – cannot distinguish • One muon causes ionisation • Second muon may cause a flash of light • The scintillator may interpret the time between the flashes is the muon decay timenot the case. • Improbable

Transition

Further Investigation How do special relativistic effects, such as time dilation, factor in to cosmic ray muon observations? • James C. Maxwell - electromagnetic waves travel at a constant speed (c) • Einstein - time was not special and was just another dimension. • As speed=distance/time, distance no longer remains the same • Time cannot be absolute

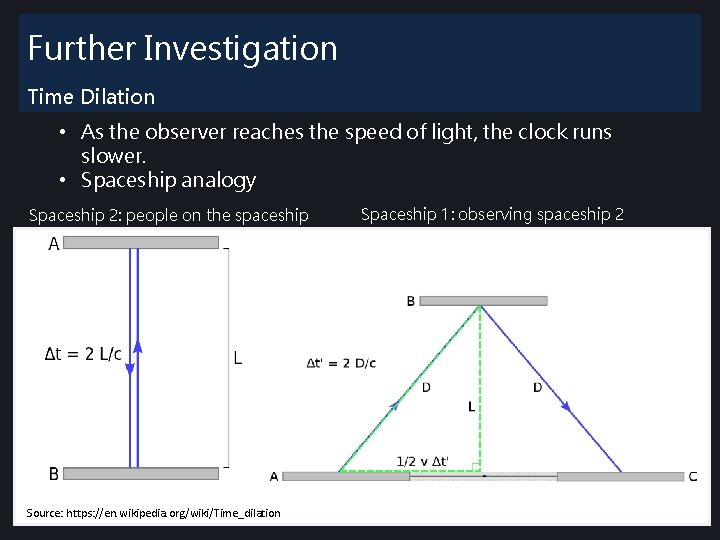
Further Investigation Time Dilation • As the observer reaches the speed of light, the clock runs slower. • Spaceship analogy Spaceship 2: people on the spaceship Source: https: //en. wikipedia. org/wiki/Time_dilation Spaceship 1: observing spaceship 2

Further Investigation How This Affects Muons • Muon – 0. 995 c • From our view point, the muons lifetime is 2. 2µs, • Explained via Special Relativity • From their point of view, they travel a shorter distance (spaceship analogy); time=distance/speed • Less time has gone by for the muons

Further Investigation Calculations •

end