Inverted Index 1 The Inverted Index The inverted

Inverted Index 1

The Inverted Index • The inverted index is a set of posting lists, one for each term in the lexicon Example: • Doc 1: A C F • Doc 2: B E D B • Doc 3: A B D F Positions increase the size of the posting list! If we only want to store doc. IDs, B’s posting list will be: 23 If we only want to store positions within doc. IDs, B’s posting list will be: (2; 1, 4), (3, 2) Or actually 2214312 2

The Inverted Index • The inverted index is a set of posting lists, one for each term in the lexicon • From now on, we will assume that posting lists are simply lists of document ids • Document ids in a posting list are sorted – A posting list is simply an increasing list of integers • The inverted index is very large – We discuss methods to compress the inverted index 3

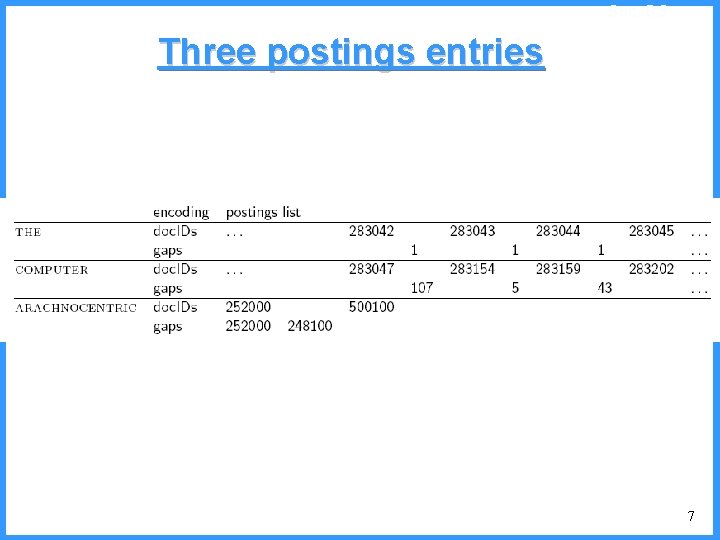
Sec. 5. 3 Postings compression • The postings file is much larger than the dictionary, factor of at least 10. • Key desideratum: store each posting compactly. • A posting for our purposes is a doc. ID. • For Reuters (800, 000 documents), we would use 32 bits per doc. ID when using 4 -byte integers. • Alternatively, we can use log 2 800, 000 ≈ 20 bits per doc. ID. • Our goal: use a lot less than 20 bits per doc. ID. 4

Sec. 5. 3 Postings: two conflicting forces • A term like arachnocentric occurs in maybe one doc out of a million – we would like to store this posting using log 2 1 M ~ 20 bits. • A term like the occurs in virtually every doc, so 20 bits/posting is too expensive. – Prefer 0/1 bitmap vector in this case 5

Sec. 5. 3 Postings file entry • We store the list of docs containing a term in increasing order of doc. ID. – computer: 33, 47, 154, 159, 202 … • Consequence: it suffices to store gaps. – 33, 14, 107, 5, 43 … • Hope: most gaps can be encoded/stored with far fewer than 20 bits. – What happens if we use fixed length encoding? 6

Sec. 5. 3 Three postings entries 7

Sec. 5. 3 Variable length encoding • Aim: – For arachnocentric, we will use ~20 bits/gap entry. – For the, we will use ~1 bit/gap entry. • If the average gap for a term is G, we want to use ~log 2 G bits/gap entry. • Key challenge: encode every integer (gap) with about as few bits as needed for that integer. • This requires a variable length encoding • Variable length codes achieve this by using short codes for small numbers 8

Types of Compression Methods • Length – Variable Byte – Variable bit • Encoding/decoding prior information – Non-parameterized – Parameterized 9

Types of Compression Methods • We will start by discussing nonparameterized methods – Variable byte – Variable bit • Afterwards we discuss two parameterized methods that are both variable bit 10

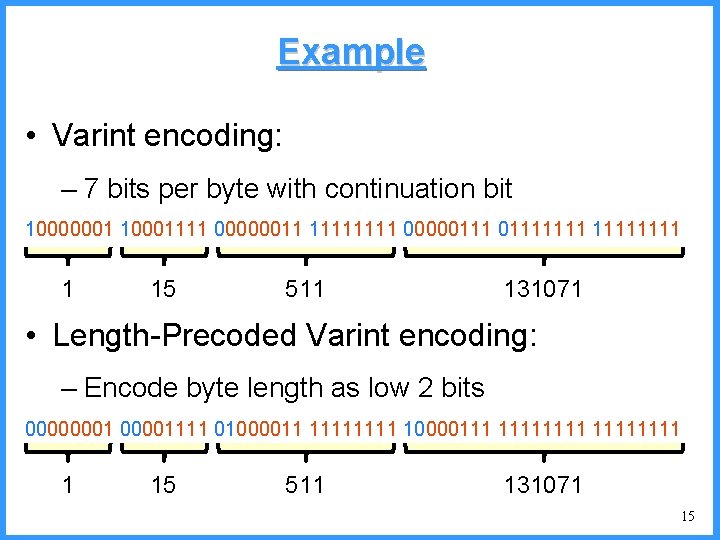
Variable Byte Compression • Document ids (=numbers) are stored using a varying number of bytes • Numbers are byte-aligned • Many compression methods have been developed. We discuss: – Varint – Length-Precoded Varint – Group Varint 11

Sec. 5. 3 Varint codes • For a gap value G, we want to use close to the fewest bytes needed to hold log 2 G bits • Begin with one byte to store G and dedicate 1 bit in it to be a continuation bit c • If G ≤ 127, binary-encode it in the 7 available bits and set c =1 • Else encode G’s higer-order 7 bits and then use additional bytes to encode the next 7 higher order bits using the same algorithm • At the end set the continuation bit of the last byte to 1 (c =1) – and for the other bytes c = 0. 12

Sec. 5. 3 Example doc. IDs 824 gaps varint code 00000110 10111000 829 215406 5 214577 10000101 00001100 10110001 Postings stored as the byte concatenation 000001101011100001010000110010110001 Key property: varint encoded postings are uniquely prefix-decodable. For a small gap (5), VB uses a whole byte. 13

Length-Precoded Varint • Currently, we must check the first bit of each byte before deciding how to proceed. • Length-Precoded Varint aims at lowering the number of “branch-and-checks” • Store each number in 1 -4 bytes. Use the first 2 bits of the first byte to indicate the number of bytes used 14

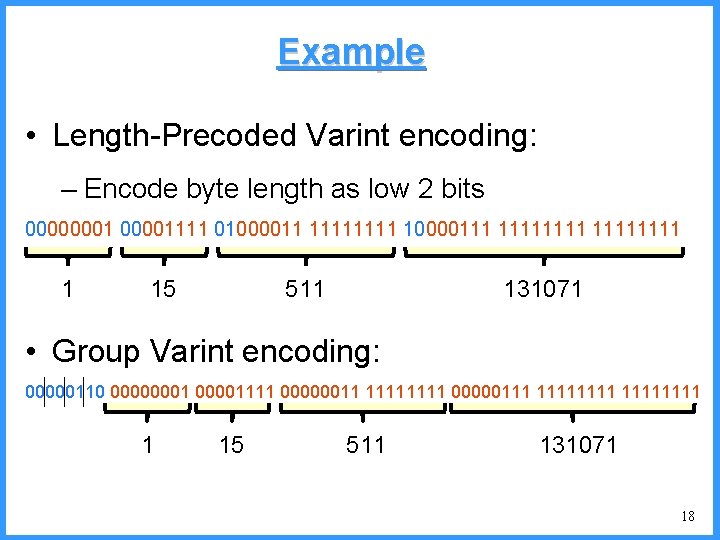
Example • Varint encoding: – 7 bits per byte with continuation bit 10000001 10001111 00000011 1111 000001111111 1 15 511 131071 • Length-Precoded Varint encoding: – Encode byte length as low 2 bits 00000001111 01000011 1111 10000111 11111111 1 15 511 131071 15

Length-Precoded Varint: Pros and Cons • Pros – Less branching – Less bit shifts • Cons – Still requires branching/bit shifts – What is the largest number that can be represented? 16

Group Varint Encoding • Introduced by Jeff Dean (Google) • Idea: encode groups of 4 values in 5 -17 bytes – Pull out 4 2 -bit binary lengths into single byte prefix – Decoding uses a 256 -entry table to determine the masks of all proceeding numbers 17

Example • Length-Precoded Varint encoding: – Encode byte length as low 2 bits 00000001111 01000011 1111 10000111 11111111 1 15 511 131071 • Group Varint encoding: 00000110 00000001111 00000011 1111 00000111 11111111 1 15 511 131071 18

Sec. 5. 3 Other Variable Unit codes • Instead of bytes, we can also use a different “unit of alignment”: 32 bits (words), 16 bits, 4 bits (nibbles). – When would smaller units of alignment be superior? When would larger units of alignment be superior? • Variable byte codes: – Used by many commercial/research systems – Good low-tech blend of variable-length coding and sensitivity to computer memory alignment matches (vs. bit-level codes, which we look at next). 19

Variable bit Codes • In variable bit codes, each code word can use a different number of bits to encode • Examples: – Unary codes – Gamma codes – Delta codes • Other well-know examples: – Golomb codes, Rice codes 20

Unary code • Represent n as n-1 1 s with a final 0. • Unary code for 3 is 110. • Unary code for 40 is 111111111111111111110. • Unary code for 80 is: 1111111111111111111110 • This doesn’t look promising, but….

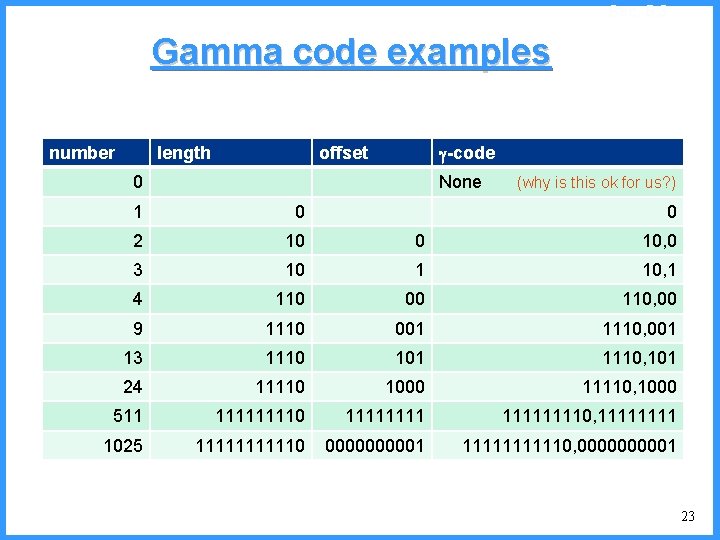
Sec. 5. 3 Gamma codes • We can compress better with bit-level codes – The Gamma code is the best known of these. • Represent a gap G as a pair length and offset • offset is G in binary, with the leading bit cut off – For example 13 → 1101 → 101 • length is the length of binary code – For 13 (1101), this is 4. • We encode length with unary code: 1110. • Gamma code of 13 is the concatenation of length and offset: 1110101 22

Sec. 5. 3 Gamma code examples number length g-code offset 0 None (why is this ok for us? ) 1 0 0 2 10 0 10, 0 3 10 1 10, 1 4 110 00 110, 00 9 1110 001 1110, 001 13 1110 101 1110, 101 24 11110 1000 11110, 1000 511 11110 111111110, 1111 1025 111110 000001 111110, 000001 23

Sec. 5. 3 Gamma code properties • G is encoded using 2 log G + 1 bits • All gamma codes have an odd number of bits • Almost within a factor of 2 of best possible, log 2 G • Gamma code is uniquely prefix-decodable • Gamma code is parameter-free 24

Delta codes • Similar to gamma codes, except that length is encoded in gamma code • Example: Compute the delta code of 9 • Decode: 1011110100 • Gamma codes = more compact for smaller numbers • Delta codes = more compact for larger numbers

Sec. 5. 3 Disadvantages of Variable Bit Codes • Machines have word boundaries – 8, 16, 32, 64 bits – Operations that cross word boundaries are slower • Compressing and manipulating at the granularity of bits can be slow • Variable byte encoding is aligned and thus potentially more efficient • Regardless of efficiency, variable byte is conceptually simpler at little additional space cost 26

Think About It • Question: Can we do binary search on a Gamma or Delta Coded sequence of increasing numbers? • Question: Can we do binary search on a Varint Coded sequence of increasing numbers? 27

Parameterized Methods • A parameterized encoding gets the probability distribution of the input symbols, and creates encodings accordingly • We will discuss 2 important parameterized methods for compression: – Canonical Huffman codes – Arithmetic encoding • These methods can also be used for compressing the dictionary! 28

Huffman Codes: Review • Surprising history of Huffman codes • Huffman codes are optimal prefix codes for symbol by symbol encoding, i. e. , codes in which no codeword is a prefix of another • Input: a set of symbols, along with a probability for each symbol A 0. 1 B 0. 2 C 0. 05 D 0. 05 E 0. 3 F 0. 2 G 0. 1 29

Creating a Huffman Code: Greedy Algorithm • Create a node for each symbol and assign with the probability of the symbol • While there is more than 1 node without a parent – choose 2 nodes with the lowest probabilities and create a new node with both nodes as children. – Assign the new node the sum of probabilities of children • The tree derived gives the code for each symbol (leftwards is 0, and rightwards is 1) 30

Problems with Huffman Codes • The tree must be stored for decoding. – Can significantly increase memory requirements • If the tree does not fit into main memory, then traversal (for decoding) is very expensive • Solution: Canonical Huffman Codes 31

Canonical Huffman Codes • Intuition: A canonical Huffman code can be efficiently described by just giving: – The list of symbols – Length of codeword of each symbol • This information is sufficient for decoding 32

Properties of Canonical Huffman Codes 1. Codewords of a given length are consecutive binary numbers 2. Given two symbols s, s’ with codewords of the same length then: cw(s) < cw(s’) if and only if s<s’ 3. The first shortest codeword is a string of 0 -s 4. The last longest codeword is a string of 1 -s 33

Properties of Canonical Huffman Codes (cont) 5. Suppose that – d is the last codeword of length i – the next length of codeword appearing in the code is j – the first codeword of length j is c Then c=2 j-i(d+1) 34

Try it • Suppose that we have the following lengths per symbol, what is the canonical Huffman code: A 3 B 2 C 4 D 4 E 2 F 3 G 3 35

Decoding • Let l 1, …, ln be the lengths of codewords appearing in the canonical code • The decoding process will use the following information, for each distinct length li: – the codeword ci of the first symbol with length li – the number of words ni of length li – easily computed using the information about symbol lengths 36

Decoding (cont) • i=0 • Repeat – i = i+1 – Let d be the word derived by reading li symbols • Until d <= ci + ni-1 • Return the d-ci+1 th symbol (in lexicographic order) of length I • Example: Decode 10001110 37

Some More Details • How do we compute the lengths for each symbol? • How do we compute the probabilities of each symbol? – model per posting list – single model for all posting lists – model for each group of posting lists (grouped by size) 38

Huffman Code Drawbacks • Each symbol is coded separately • Each symbol uses a whole number of bits • Can be very inefficient when there are extremely likely/unlikely values 39

How Much can We Compress? • Given: (1) A set of symbols, (2) Each symbol s has an associated probability P(s) • Shannon’s lower bound on the average number of bits per symbol needed is: s –P(s) log P(s) – Roughly speaking, each symbol s with probability P(s) needs at least –log P(s) bits to represent – Example: the outcome of a fair coin needs –log 0. 5=1 bit to represent • Ideally, we aim to find a compression method that reaches Shannon’s bound 40

Example • Suppose A has probability 0. 99 and B has probability 0. 01. • How many bits will Huffman’s code use for 10 A-s? • Shannon’s bound gives us a requirement of - log(0. 99)=0. 015 bits per word, i. e. , only 0. 15 bits in total! • Inefficiency of Huffman’s code is bounded from above by where sm is the most likely symbol 41

Arithmetic Coding • Comes closer to Shannon’s bound by coding symbols together • Input: Set of symbols S with probabilities, input text s 1, …, sn • Output: length n of the input text and a number (written in binary) in [0, 1) • In order to explain the algorithm, numbers will be shown as decimal, but obviously they are always binary 42

Arithemetic. Encoding(s 1…sn) • low : = 0 • high : = 1 • for i=1 to n do (low, high) : = Restrict(low, high, si) • return any number between low and high 43

Restrict(low, high, si) • low_bound : = sum{P(s) | s S and s<si} • high_bound : = low_bound + P(si) • range : = high - low • new_low : = low + range*low_bound • new_high : = low + range*high_bound • return (new_low, new_high) 44

Arithmetic. Decoding(k, n) • low : = 0 • high : = 1 • for i = 1 to n do – for each s S do • (new_low, new_high) : = Restrict(low, high, s) – if new_low k < new_high then • Output “s” • low : = new_low • high : = new_high • break 45

Think about it • Decode the string 0. 34 of length 3 • In general, what is the size of the encoding of an input? – to store a number in an interval of size high-low, we need –log(high-low) bits – The size of the final interval is needs , and bits 46

Adaptive Arithmetic Coding • In order to decode, the probabilities of each symbol must be known. – This must be stored, which adds to overhead • The probabilities may change over the course of the text – Cannot be modeled thus far • In adaptive arithmetic coding the encoder (and decoder) compute the probabilities on the fly by counting symbol frequencies 47

An example - I • String bccb from the alphabet {a, b, c} • Zero-frequency problem solved initializing at 1 all character counters • When the first b is to be coded all symbols have a 33% probability (why? ) • The arithmetic coder maintains two numbers, low and high, which represent a subinterval [low, high) of the range [0, 1) • Initially low=0 and high=1 48

An example - II • The range between low and high is divided between the symbols of the alphabet, according to their probabilities high 1 (P[c]=1/3) c (P[b]=1/3) b (P[a]=1/3) a 0. 6667 0. 3333 low 0 49

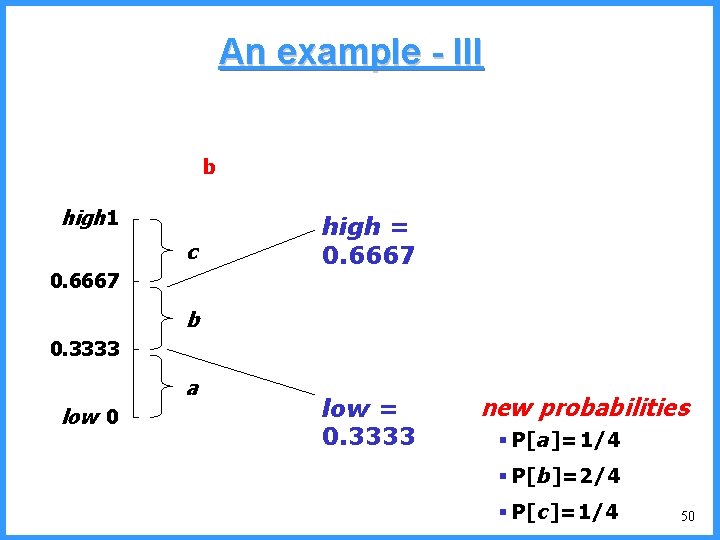
An example - III b high 1 c 0. 6667 high = 0. 6667 b 0. 3333 a low 0 low = 0. 3333 new probabilities § P[a]=1/4 § P[b]=2/4 § P[c]=1/4 50

An example - IV high (P[c]=1/4) 0. 6667 0. 5834 0. 4167 low c high = 0. 6667 0. 3333 new probabilities • P[a]=1/5 b (P[b]=2/4) (P[a]=1/4) c • P[b]=2/5 • P[c]=2/5 a low = 0. 5834 51

An example - V high c 0. 6667 c (P[c]=2/5) high = 0. 6667 • P[a]=1/6 0. 6334 (P[a]=1/5) low • P[b]=2/6 b (P[b]=2/5) 0. 6001 0. 5834 new probabilities • P[c]=3/6 a low = 0. 6334 52

An example - VI high b 0. 6667 (P[c]=3/6) c 0. 6501 b (P[b]=2/6) (P[a]=1/6) low 0. 6390 0. 6334 a high = 0. 6501 • Final interval [0. 6390, 0. 6501) • we can send 0. 64 low = 0. 6390 53

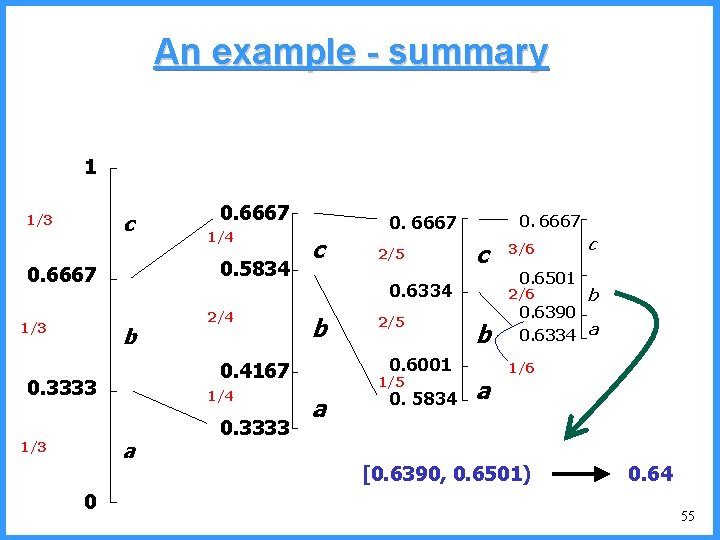
An example - summary • Starting from the range between 0 and 1 we restrict ourself each time to the subinterval that codify the given symbol • At the end the whole sequence can be codified by any of the numbers in the final range (but mind the brackets. . . ) 54

An example - summary 1 c 1/3 b 1/4 a 0 2/4 c 0. 3333 0. 6667 2/5 0. 6667 c 0. 6334 b 2/5 0. 6001 0. 4167 0. 3333 1/4 0. 5834 0. 6667 1/3 0. 6667 1/5 a 0. 5834 3/6 0. 6501 2/6 b a c b 0. 6390 0. 6334 a 1/6 [0. 6390, 0. 6501) 0. 64 55

Tirgul Questions 56

Gamma Codes and Delta Codes • Gamma Codes: – Encode 7 – Decode 11001 – Given a series of bits, divide into separate Gamma Codes: 1111010011010 • Delta Codes: – Encode 57 57

Canonical Huffman Codes אות תדירות A 0. 2 B 0. 2 C 0. 4 D 0. 2 • Give a Canonical Huffman code for this alphabet. • How many different solutions are there? 58

Arithmetic Coding • Suppose that we have symbols – A with probability 0. 2 – B with probability 0. 3 – C with probability 0. 5 • Encode ACB using arithmetic coding • Encode AAB using adaptive arithmetic coding 59