Inverted Index 1 The Inverted Index The inverted

Inverted Index 1

The Inverted Index • The inverted index is a set of posting lists, one for each term in the lexicon Example: • Doc 1: A C F • Doc 2: B E D B • Doc 3: A B D F Positions increase the size of the posting list! If we only want to store doc. IDs, B’s posting list will be: 23 If we only want to store positions within doc. IDs, B’s posting list will be: (2; 1, 4), (3, 2) Or actually 2214312 2

The Inverted Index • The inverted index is a set of posting lists, one for each term in the lexicon • From now on, we will assume that posting lists are simply lists of document ids • Document ids in a posting list are sorted – A posting list is simply an increasing list of integers • The inverted index is very large – We discuss methods to compress the inverted index 3

Sec. 5. 3 Postings compression • The postings file is much larger than the dictionary, factor of at least 10. • Key desideratum: store each posting compactly. • A posting for our purposes is a doc. ID. • For Reuters (800, 000 documents), we would use 32 bits per doc. ID when using 4 -byte integers. • Alternatively, we can use log 2 800, 000 ≈ 20 bits per doc. ID. • Our goal: use a lot less than 20 bits per doc. ID. 4

Sec. 5. 3 Postings: two conflicting forces • A term like arachnocentric occurs in maybe one doc out of a million – we would like to store this posting using log 2 1 M ~ 20 bits. • A term like the occurs in virtually every doc, so 20 bits/posting is too expensive. – Prefer 0/1 bitmap vector in this case 5

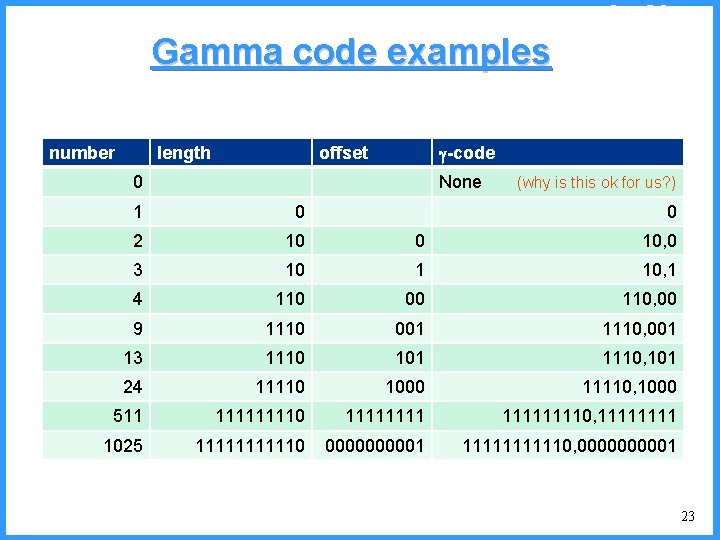
Sec. 5. 3 Postings file entry • We store the list of docs containing a term in increasing order of doc. ID. – computer: 33, 47, 154, 159, 202 … • Consequence: it suffices to store gaps. – 33, 14, 107, 5, 43 … • Hope: most gaps can be encoded/stored with far fewer than 20 bits. – What happens if we use fixed length encoding? 6

Sec. 5. 3 Three postings entries 7

Sec. 5. 3 Variable length encoding • Aim: – For arachnocentric, we will use ~20 bits/gap entry. – For the, we will use ~1 bit/gap entry. • If the average gap for a term is G, we want to use ~log 2 G bits/gap entry. • Key challenge: encode every integer (gap) with about as few bits as needed for that integer. • This requires a variable length encoding • Variable length codes achieve this by using short codes for small numbers 8

Types of Compression Methods • Length – Variable Byte – Variable bit • Encoding/decoding prior information – Non-parameterized – Parameterized 9

Types of Compression Methods • We will start by discussing nonparameterized methods – Variable byte – Variable bit • Afterwards we discuss two parameterized methods that are both variable bit 10

Variable Byte Compression • Document ids (=numbers) are stored using a varying number of bytes • Numbers are byte-aligned • Many compression methods have been developed. We discuss: – Varint – Length-Precoded Varint – Group Varint 11

Sec. 5. 3 Varint codes • For a gap value G, we want to use close to the fewest bytes needed to hold log 2 G bits • Begin with one byte to store G and dedicate 1 bit in it to be a continuation bit c • If G ≤ 127, binary-encode it in the 7 available bits and set c =1 • Else encode G’s higer-order 7 bits and then use additional bytes to encode the next 7 higher order bits using the same algorithm • At the end set the continuation bit of the last byte to 1 (c =1) – and for the other bytes c = 0. 12

Sec. 5. 3 Example doc. IDs 824 gaps varint code 00000110 10111000 829 215406 5 214577 10000101 00001100 10110001 Postings stored as the byte concatenation 000001101011100001010000110010110001 Key property: varint encoded postings are uniquely prefix-decodable. For a small gap (5), VB uses a whole byte. 13

Length-Precoded Varint • Currently, we must check the first bit of each byte before deciding how to proceed. • Length-Precoded Varint aims at lowering the number of “branch-and-checks” • Store each number in 1 -4 bytes. Use the first 2 bits of the first byte to indicate the number of bytes used 14

Example • Varint encoding: – 7 bits per byte with continuation bit 10000001 10001111 00000011 1111 000001111111 1 15 511 131071 • Length-Precoded Varint encoding: – Encode byte length as low 2 bits 00000001111 01000011 1111 10000111 11111111 1 15 511 131071 15

Length-Precoded Varint: Pros and Cons • Pros – Less branching – Less bit shifts • Cons – Still requires branching/bit shifts – What is the largest number that can be represented? 16

Group Varint Encoding • Introduced by Jeff Dean (Google) • Idea: encode groups of 4 values in 5 -17 bytes – Pull out 4 2 -bit binary lengths into single byte prefix – Decoding uses a 256 -entry table to determine the masks of all proceeding numbers 17

Example • Length-Precoded Varint encoding: – Encode byte length as low 2 bits 00000001111 01000011 1111 10000111 11111111 1 15 511 131071 • Group Varint encoding: 00000110 00000001111 00000011 1111 00000111 11111111 1 15 511 131071 18

Sec. 5. 3 Other Variable Unit codes • Instead of bytes, we can also use a different “unit of alignment”: 32 bits (words), 16 bits, 4 bits (nibbles). – When would smaller units of alignment be superior? When would larger units of alignment be superior? • Variable byte codes: – Used by many commercial/research systems – Good low-tech blend of variable-length coding and sensitivity to computer memory alignment matches (vs. bit-level codes, which we look at next). 19

Variable bit Codes • In variable bit codes, each code word can use a different number of bits to encode • Examples: – Unary codes – Gamma codes – Delta codes • Other well-know examples: – Golomb codes, Rice codes 20

Unary code • Represent n as n-1 1 s with a final 0. • Unary code for 3 is 110. • Unary code for 40 is 111111111111111111110. • Unary code for 80 is: 1111111111111111111110 • This doesn’t look promising, but….

Sec. 5. 3 Gamma codes • We can compress better with bit-level codes – The Gamma code is the best known of these. • Represent a gap G as a pair length and offset • offset is G in binary, with the leading bit cut off – For example 13 → 1101 → 101 • length is the length of binary code – For 13 (1101), this is 4. • We encode length with unary code: 1110. • Gamma code of 13 is the concatenation of length and offset: 1110101 22

Sec. 5. 3 Gamma code examples number length g-code offset 0 None (why is this ok for us? ) 1 0 0 2 10 0 10, 0 3 10 1 10, 1 4 110 00 110, 00 9 1110 001 1110, 001 13 1110 101 1110, 101 24 11110 1000 11110, 1000 511 11110 111111110, 1111 1025 111110 000001 111110, 000001 23

Try it • Encode 7 • Decode 11001 • Given a series of bits, divide into separate Gamma Codes: 1111010011010 24

Sec. 5. 3 Gamma code properties • G is encoded using 2 log G + 1 bits • All gamma codes have an odd number of bits • Almost within a factor of 2 of best possible, log 2 G • Gamma code is uniquely prefix-decodable • Gamma code is parameter-free 25

Delta codes • Similar to gamma codes, except that length is encoded in gamma code • Example: Compute the delta code of 9 • Decode: 1011110100 • Gamma codes = more compact for smaller numbers • Delta codes = more compact for larger numbers

Sec. 5. 3 Disadvantages of Variable Bit Codes • Machines have word boundaries – 8, 16, 32, 64 bits – Operations that cross word boundaries are slower • Compressing and manipulating at the granularity of bits can be slow • Variable byte encoding is aligned and thus potentially more efficient • Regardless of efficiency, variable byte is conceptually simpler at little additional space cost 27

Think About It • Question: Can we do binary search on a Gamma or Delta Coded sequence of increasing numbers? • Question: Can we do binary search on a Varint Coded sequence of increasing numbers? 28

Parameterized Methods • A parameterized encoding gets the probability distribution of the input symbols, and creates encodings accordingly • We will discuss 2 important parameterized methods for compression: – Canonical Huffman codes – Arithmetic encoding • These methods can also be used for compressing the dictionary! 29

Huffman Codes: Review • Surprising history of Huffman codes • Huffman codes are optimal prefix codes for symbol by symbol encoding, i. e. , codes in which no codeword is a prefix of another • Input: a set of symbols, along with a probability for each symbol A 0. 1 B 0. 2 C 0. 05 D 0. 05 E 0. 3 F 0. 2 G 0. 1 30

Creating a Huffman Code: Greedy Algorithm • Create a node for each symbol and assign with the probability of the symbol • While there is more than 1 node without a parent – choose 2 nodes with the lowest probabilities and create a new node with both nodes as children. – Assign the new node the sum of probabilities of children • The tree derived gives the code for each symbol (leftwards is 0, and rightwards is 1) 31

Problems with Huffman Codes • The tree must be stored for decoding. – Can significantly increase memory requirements • If the tree does not fit into main memory, then traversal (for decoding) is very expensive • Solution: Canonical Huffman Codes 32

Canonical Huffman Codes • Intuition: A canonical Huffman code can be efficiently described by just giving: – The list of symbols – Length of codeword of each symbol • This information is sufficient for decoding 33

Properties of Canonical Huffman Codes 1. Codewords of a given length are consecutive binary numbers 2. Given two symbols s, s’ with codewords of the same length then: cw(s) < cw(s’) if and only if s<s’ 3. The first shortest codeword is a string of 0 -s 4. The last longest codeword is a string of 1 -s 34

Properties of Canonical Huffman Codes (cont) 5. Suppose that – d is the last codeword of length i – the next length of codeword appearing in the code is j – the first codeword of length j is c Then c=2 j-i(d+1) 35

Try it • Suppose that we have the following lengths per symbol, what is the canonical Huffman code: A 3 B 2 C 4 D 4 E 2 F 3 G 3 36

Decoding • Let l 1, …, ln be the lengths of codewords appearing in the canonical code • The decoding process will use the following information, for each distinct length li: – the codeword ci of the first symbol with length li – the number of words ni of length li – easily computed using the information about symbol lengths 37

Decoding (cont) • i=0 • Repeat – i = i+1 – Let d be the word derived by reading li symbols • Until d <= ci + ni-1 • Return the d-ci+1 th symbol (in lexicographic order) of length I • Example: Decode 10001110 38

Some More Details • How do we compute the lengths for each symbol? • How do we compute the probabilities of each symbol? – model per posting list – single model for all posting lists – model for each group of posting lists (grouped by size) 39

Huffman Code Drawbacks • Each symbol is coded separately • Each symbol uses a whole number of bits • Can be very inefficient when there are extremely likely/unlikely values 40

How Much can We Compress? • Given: (1) A set of symbols, (2) Each symbol s has an associated probability P(s) • Shannon’s lower bound on the average number of bits per symbol needed is: s –P(s) log P(s) – Roughly speaking, each symbol s with probability P(s) needs at least –log P(s) bits to represent – Example: the outcome of a fair coin needs –log 0. 5=1 bit to represent • Ideally, we aim to find a compression method that reaches Shannon’s bound 41

Example • Suppose A has probability 0. 99 and B has probability 0. 01. • How many bits will Huffman’s code use for 10 A-s? • Shannon’s bound gives us a requirement of - log(0. 99)=0. 015 bits per word, i. e. , only 0. 15 bits in total! • Inefficiency of Huffman’s code is bounded from above by where sm is the most likely symbol 42

Arithmetic Coding • Comes closer to Shannon’s bound by coding symbols together • Input: Set of symbols S with probabilities, input text s 1, …, sn • Output: length n of the input text and a number (written in binary) in [0, 1) • In order to explain the algorithm, numbers will be shown as decimal, but obviously they are always binary 43

Arithemetic. Encoding(s 1…sn) • low : = 0 • high : = 1 • for i=1 to n do (low, high) : = Restrict(low, high, si) • return any number between low and high 44

Restrict(low, high, si) • low_bound : = sum{P(s) | s S and s<si} • high_bound : = low_bound + P(si) • range : = high - low • new_low : = low + range*low_bound • new_high : = low + range*high_bound • return (new_low, new_high) 45

Example • Suppose that we have symbols – A with probability 0. 2 – B with probability 0. 3 – C with probability 0. 5 • Encode ACCB 46

Arithmetic. Decoding(k, n) • low : = 0 • high : = 1 • for i = 1 to n do – for each s S do • (new_low, new_high) : = Restrict(low, high, s) – if new_low k < new_high then • Output “s” • low : = new_low • high : = new_high • break 47

Think about it • Decode the string 0. 34 of length 3 • In general, what is the size of the encoding of an input? – to store a number in an interval of size high-low, we need –log(high-low) bits – The size of the final interval is needs , and bits 48

Adaptive Arithmetic Coding • In order to decode, the probabilities of each symbol must be known. – This must be stored, which adds to overhead • The probabilities may change over the course of the text – Cannot be modeled thus far • In adaptive arithmetic coding the encoder (and decoder) compute the probabilities on the fly by counting symbol frequencies 49

An example - I n n n String bccb from the alphabet {a, b, c} Zero-frequency problem solved initializing at 1 all character counters When the first b is to be coded all symbols have a 33% probability (why? ) The arithmetic coder maintains two numbers, low and high, which represent a subinterval [low, high) of the range [0, 1) Initially low=0 and high=1 50

An example - II n The range between low and high is divided between the symbols of the alphabet, according to their probabilities high 1 (P[c]=1/3) c (P[b]=1/3) b (P[a]=1/3) a 0. 6667 0. 3333 low 0 51

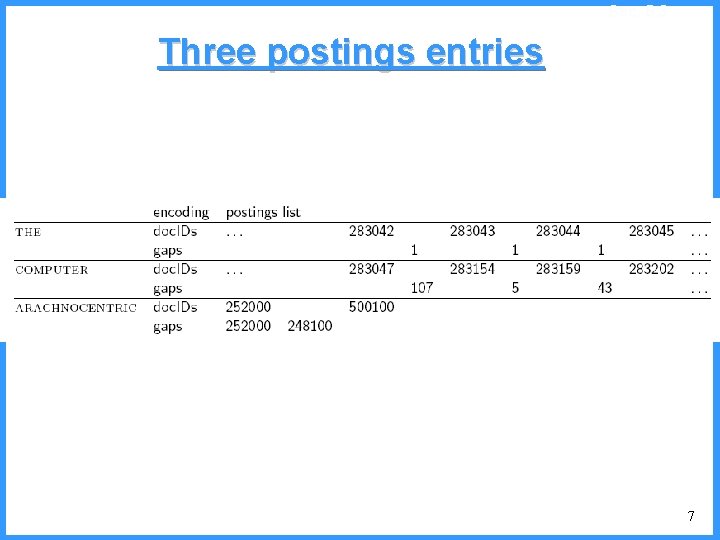
An example - III b high 1 c 0. 6667 high = 0. 6667 b 0. 3333 a low 0 low = 0. 3333 new probabilities § P[a]=1/4 § P[b]=2/4 § P[c]=1/4 52

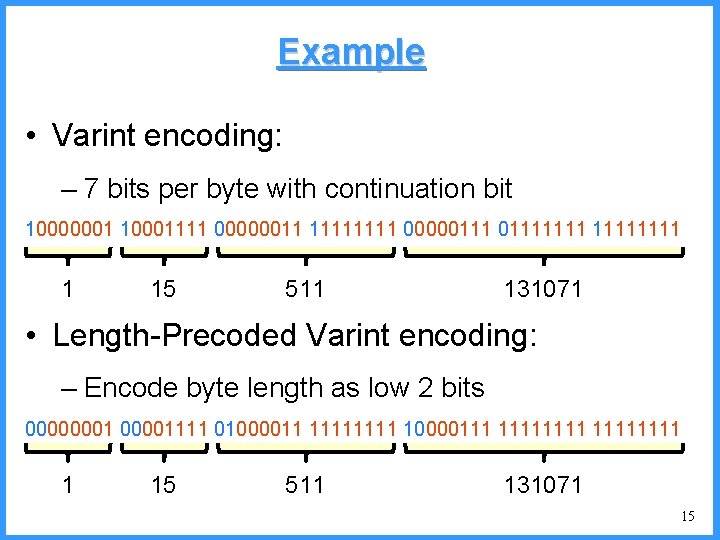
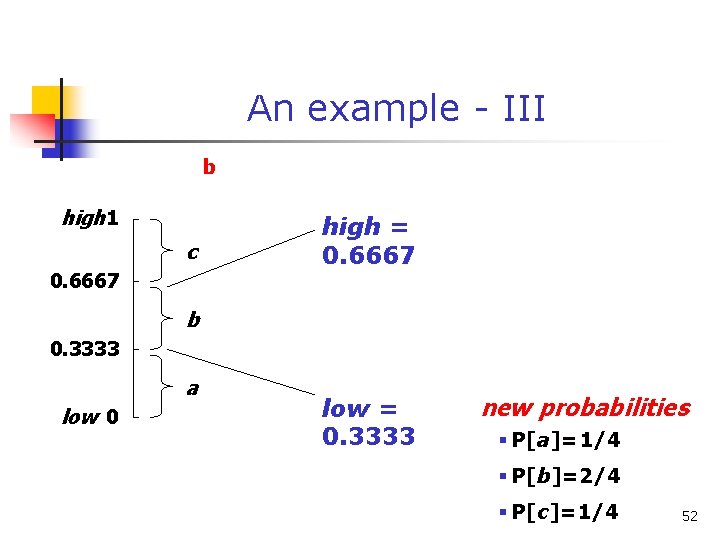
An example - IV high (P[c]=1/4) 0. 6667 0. 5834 0. 4167 low c high = 0. 6667 b (P[b]=2/4) (P[a]=1/4) c 0. 3333 new probabilities n P[a]=1/5 n P[b]=2/5 n P[c]=2/5 a low = 0. 5834 53

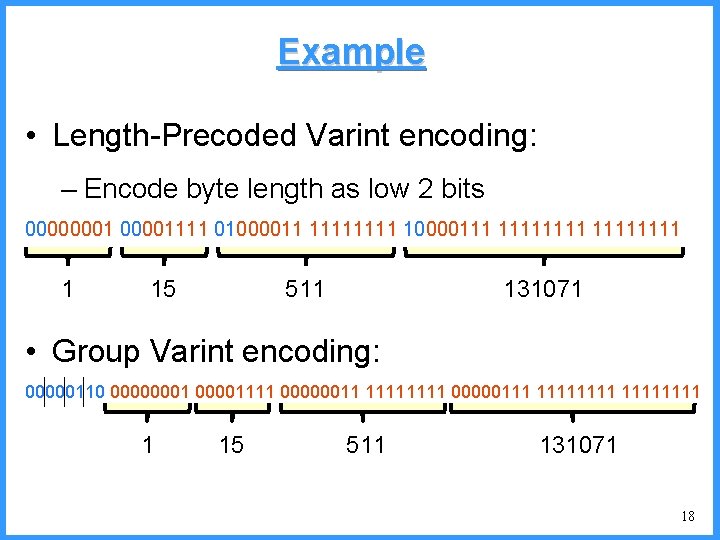
An example - V high c 0. 6667 c (P[c]=2/5) high = 0. 6667 0. 6334 b (P[b]=2/5) (P[a]=1/5) low 0. 6001 0. 5834 new probabilities n P[a]=1/6 n P[b]=2/6 n P[c]=3/6 a low = 0. 6334 54

An example - VI high b 0. 6667 (P[c]=3/6) c high = 0. 6501 n 0. 6501 b (P[b]=2/6) (P[a]=1/6) low 0. 6390 0. 6334 a n Final interval [0. 6390, 0. 6501) we can send 0. 64 low = 0. 6390 55

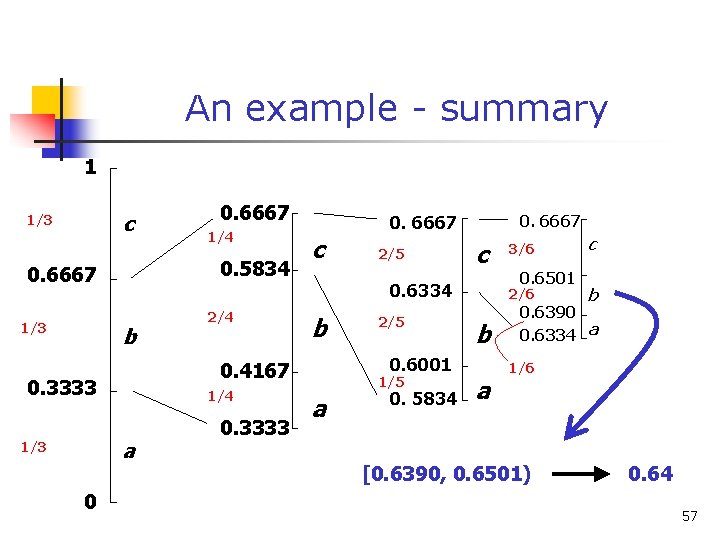
An example - summary n n Starting from the range between 0 and 1 we restrict ourself each time to the subinterval that codify the given symbol At the end the whole sequence can be codified by any of the numbers in the final range (but mind the brackets. . . ) 56

An example - summary 1 c 1/3 b 1/4 a 0 2/4 c 0. 3333 0. 6667 2/5 0. 6667 c 0. 6334 b 2/5 0. 6001 0. 4167 0. 3333 1/4 0. 5834 0. 6667 1/3 0. 6667 1/5 a 0. 5834 3/6 0. 6501 2/6 b a c b 0. 6390 0. 6334 a 1/6 [0. 6390, 0. 6501) 0. 64 57