Inverse Variation Lesson 5 6 Algebra 1 Additional
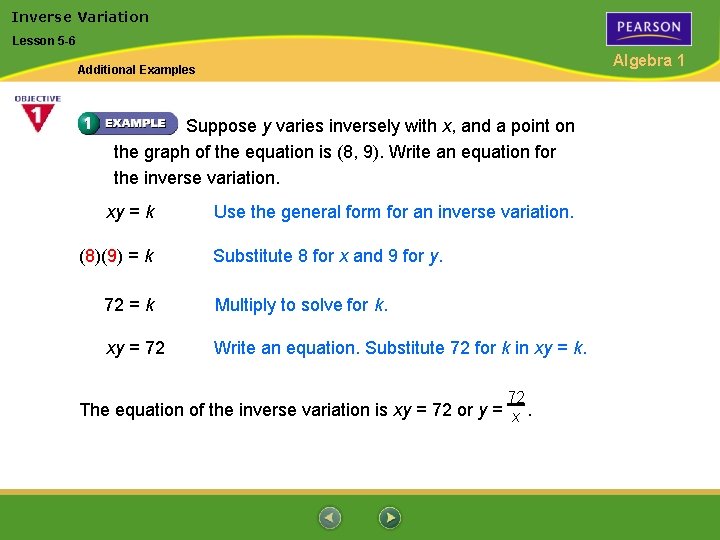
Inverse Variation Lesson 5 -6 Algebra 1 Additional Examples Suppose y varies inversely with x, and a point on the graph of the equation is (8, 9). Write an equation for the inverse variation. xy = k (8)(9) = k Use the general form for an inverse variation. Substitute 8 for x and 9 for y. 72 = k Multiply to solve for k. xy = 72 Write an equation. Substitute 72 for k in xy = k. 72 The equation of the inverse variation is xy = 72 or y = x.
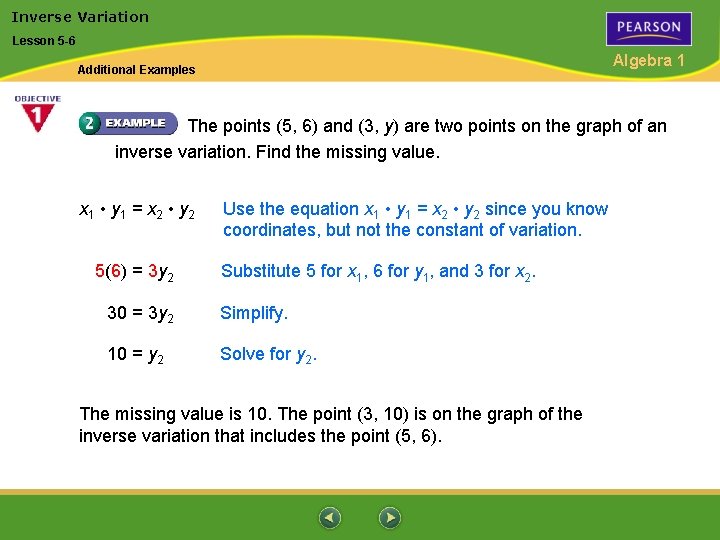
Inverse Variation Lesson 5 -6 Algebra 1 Additional Examples The points (5, 6) and (3, y) are two points on the graph of an inverse variation. Find the missing value. x 1 • y 1 = x 2 • y 2 5(6) = 3 y 2 Use the equation x 1 • y 1 = x 2 • y 2 since you know coordinates, but not the constant of variation. Substitute 5 for x 1, 6 for y 1, and 3 for x 2. 30 = 3 y 2 Simplify. 10 = y 2 Solve for y 2. The missing value is 10. The point (3, 10) is on the graph of the inverse variation that includes the point (5, 6).
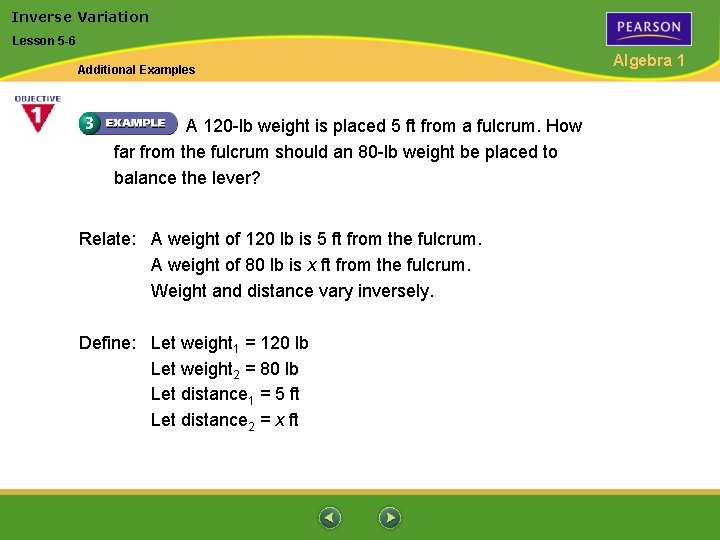
Inverse Variation Lesson 5 -6 Additional Examples A 120 -lb weight is placed 5 ft from a fulcrum. How far from the fulcrum should an 80 -lb weight be placed to balance the lever? Relate: A weight of 120 lb is 5 ft from the fulcrum. A weight of 80 lb is x ft from the fulcrum. Weight and distance vary inversely. Define: Let weight 1 = 120 lb Let weight 2 = 80 lb Let distance 1 = 5 ft Let distance 2 = x ft Algebra 1
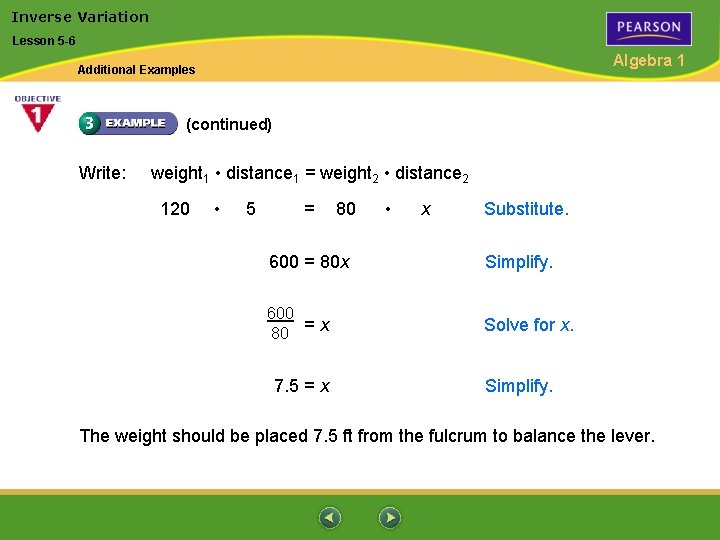
Inverse Variation Lesson 5 -6 Algebra 1 Additional Examples (continued) Write: weight 1 • distance 1 = weight 2 • distance 2 120 • 5 = 80 • x Substitute. 600 = 80 x Simplify. 600 80 = x Solve for x. 7. 5 = x Simplify. The weight should be placed 7. 5 ft from the fulcrum to balance the lever.

Inverse Variation Lesson 5 -6 Algebra 1 Additional Examples Decide if each data set represents a direct variation or an inverse variation. Then write an equation to model the data. a. x 3 5 10 y 10 6 3 The values of y seem to vary inversely with the values of x. Check each product xy. xy: 3(10) = 30 5(6) = 30 The product of xy is the same for all pairs of data. So, this is an inverse variation, and k = 30. The equation is xy = 30. 10(3) = 30
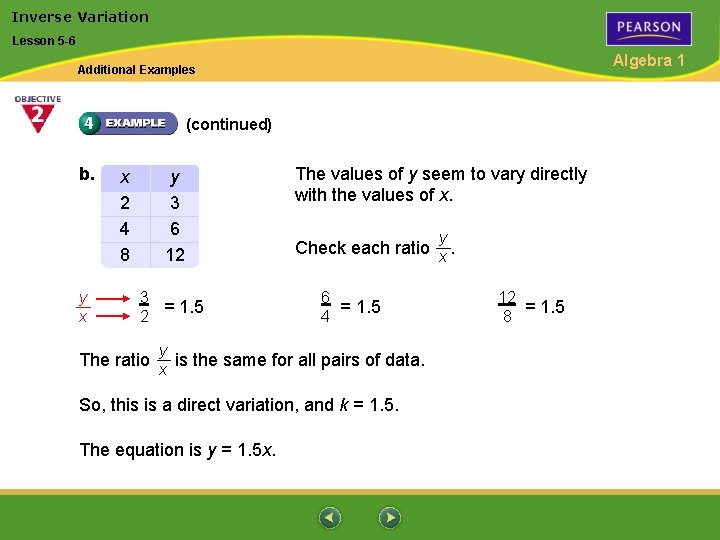
Inverse Variation Lesson 5 -6 Algebra 1 Additional Examples (continued) b. y x x 2 4 8 y 3 6 12 3 = 1. 5 2 The values of y seem to vary directly with the values of x. y Check each ratio x. 6 = 1. 5 4 y The ratio x is the same for all pairs of data. So, this is a direct variation, and k = 1. 5. The equation is y = 1. 5 x. 12 = 1. 5 8
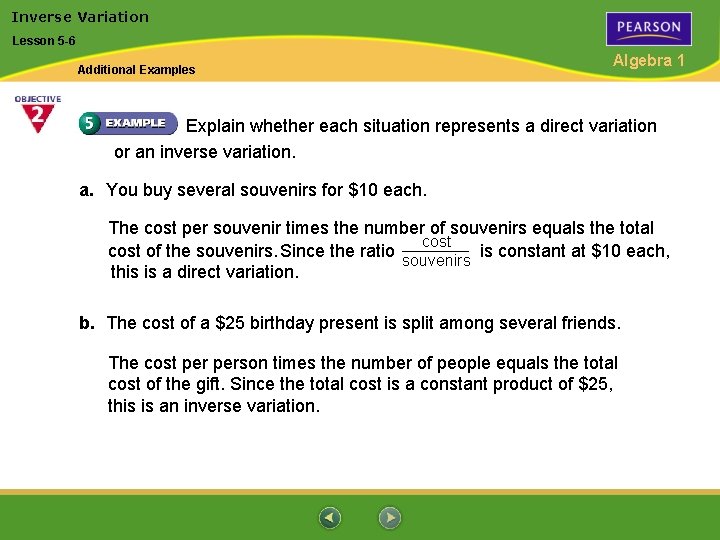
Inverse Variation Lesson 5 -6 Additional Examples Algebra 1 Explain whether each situation represents a direct variation or an inverse variation. a. You buy several souvenirs for $10 each. The cost per souvenir times the number of souvenirs equals the total cost of the souvenirs. Since the ratio is constant at $10 each, souvenirs this is a direct variation. b. The cost of a $25 birthday present is split among several friends. The cost person times the number of people equals the total cost of the gift. Since the total cost is a constant product of $25, this is an inverse variation.
- Slides: 7