Inverse Probability Weights EPID 799 C Lecture 21

Inverse Probability Weights EPID 799 C, Lecture 21 Monday, Nov. 12, 2018

Acknowledgements • Brian Pence (EPID 718) • Alan Brookhart and Steve Cole (EPID 722) • Mike and Nick!

Intro to IP Weights • In epidemiological analyses, weights can address a range of issues such as: • • Sampling / selection Confounding Missingness Censoring • Think about weights as reshaping your data: up-weight or down-weight observations with the goal of removing a particular bias.

Intro to IP Weights • Weights are calculated based on the probability of: • • Selection into the study population Address sampling bias or generalizability Receipt of a treatment or exposure Address confounding Observation at a visit Address missingness Remaining under observation Address censoring • Weight = 1/Probability • Hence, inverse probability

Intro to IP Weights To address this issue… …use the probability of… Sampling / Selection into the study population Confounding Receipt of a treatment or exposure Missingness Observation at a visit Censoring Remaining under observation …to apply these weights IPSW IPTW IPOW IPCW
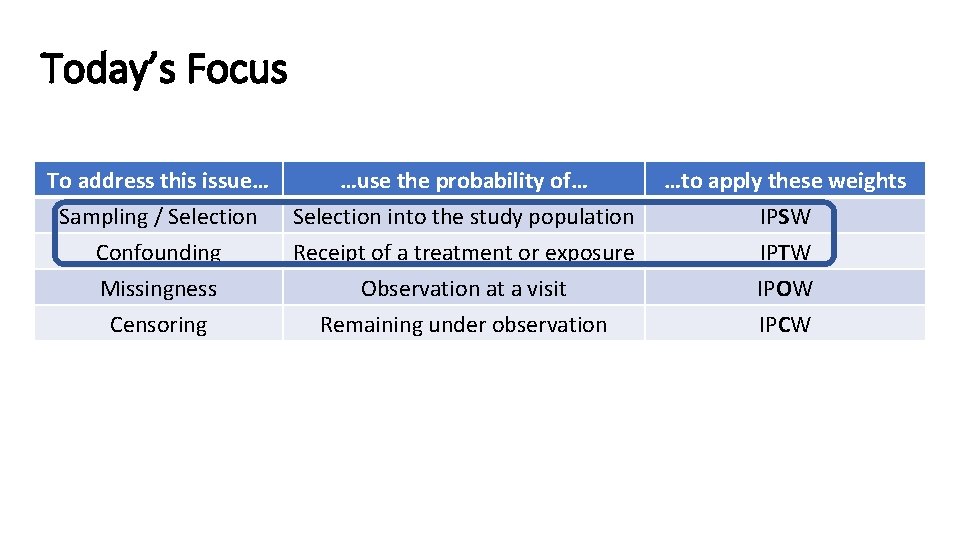
Today’s Focus To address this issue… …use the probability of… Sampling / Selection into the study population Confounding Receipt of a treatment or exposure Missingness Observation at a visit Censoring Remaining under observation …to apply these weights IPSW IPTW IPOW IPCW

Discuss on Wed (in context of survival analysis) To address this issue… …use the probability of… Sampling / Selection into the study population Confounding Receipt of a treatment or exposure Missingness Observation at a visit Censoring Remaining under observation …to apply these weights IPSW IPTW IPOW IPCW

IP Weights in R • Disclaimer: I’m still new to this, too! • “By hand” – best way for me to learn. Simple step-by-step approach. • Probably at the expense of efficiency. • Packages can implement more sophisticated and efficient approaches. • ipw for IPTW, IPCW • Alan Brookhart’s work in progress ipwrisk • So far, just use to check my work – but could be used exclusively.

Intuition from Sampling Weights (IPSW) • Study population: Our analysis sample. • Target population: The population about whom we want to infer results from our analysis. • Study population �Target population: • Sample may not be a perfect representation of the population. • Potentially due to: not randomly selected, use of cluster sampling or stratification, systematic differences in likelihood of study participation. • IPSW allows us to make inferences based on a sample that does not look exactly like the population from which it was drawn.

IPSW Example: Influenza among Older Adults • Simulated data set to demonstrate weighting approaches (will be used in EPID 718). • Estimate the effect of influenza vaccination on influenza infection among adults aged 65 and older in the US during the 2016 -2017 flu season.

IPSW Example: Influenza among Older Adults • Study population n=20, 000 identified in Medicare claims. • Stratified by age yielding the following distribution: Age range 65 -69 70 -74 75 -79 80 -84 ≥ 85 Total Sample 4, 000 4, 018 4, 000 3, 912 4, 070 20, 000
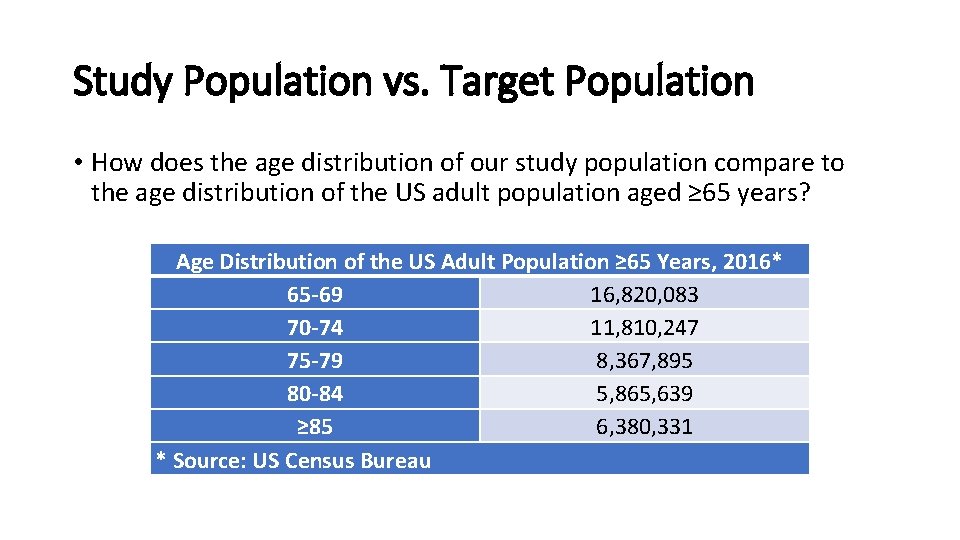
Study Population vs. Target Population • How does the age distribution of our study population compare to the age distribution of the US adult population aged ≥ 65 years? Age Distribution of the US Adult Population ≥ 65 Years, 2016* 65 -69 16, 820, 083 70 -74 11, 810, 247 75 -79 8, 367, 895 80 -84 5, 865, 639 ≥ 85 6, 380, 331 * Source: US Census Bureau

R Markdown Example • Are influenza vaccination and infection associated with age group? • If so, how should we account for differing age distributions to infer results to the target population? • Sampling weights (IPSW).
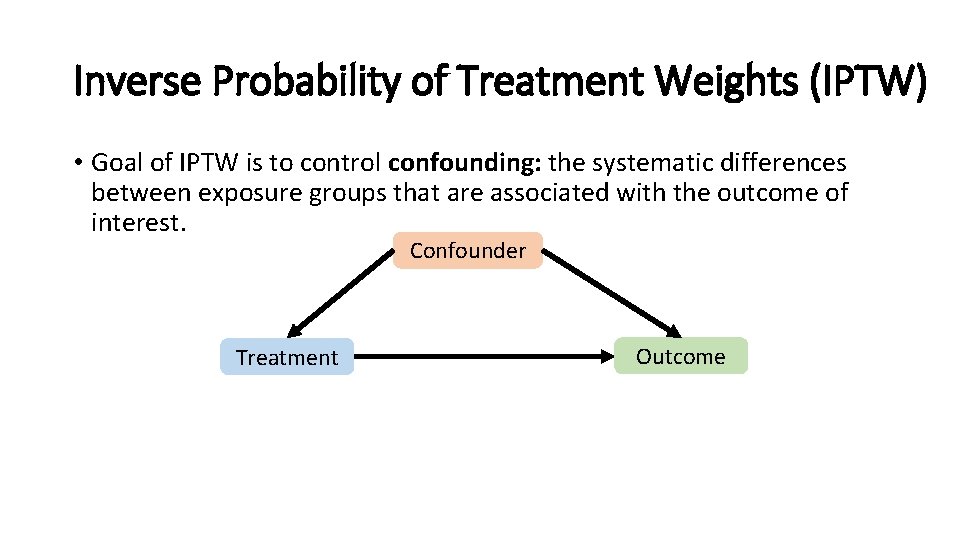
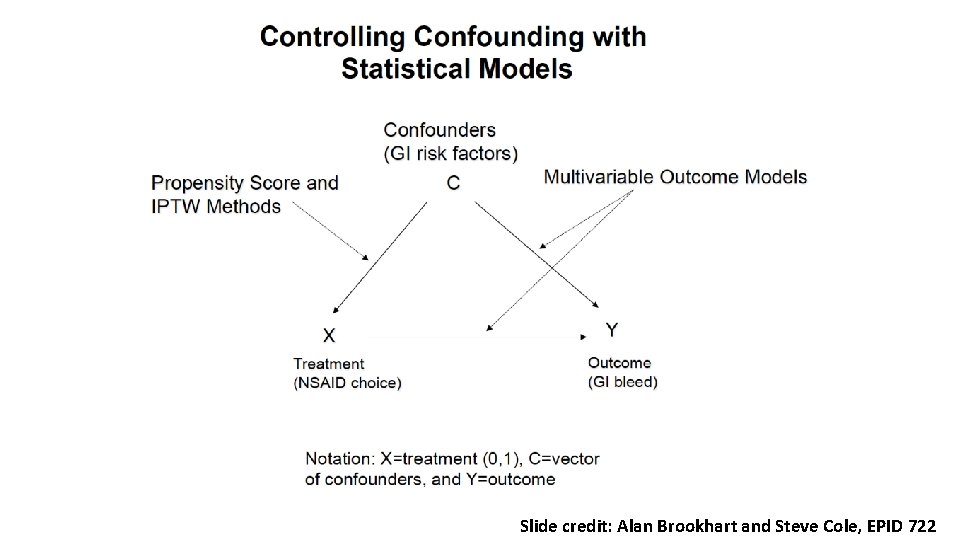
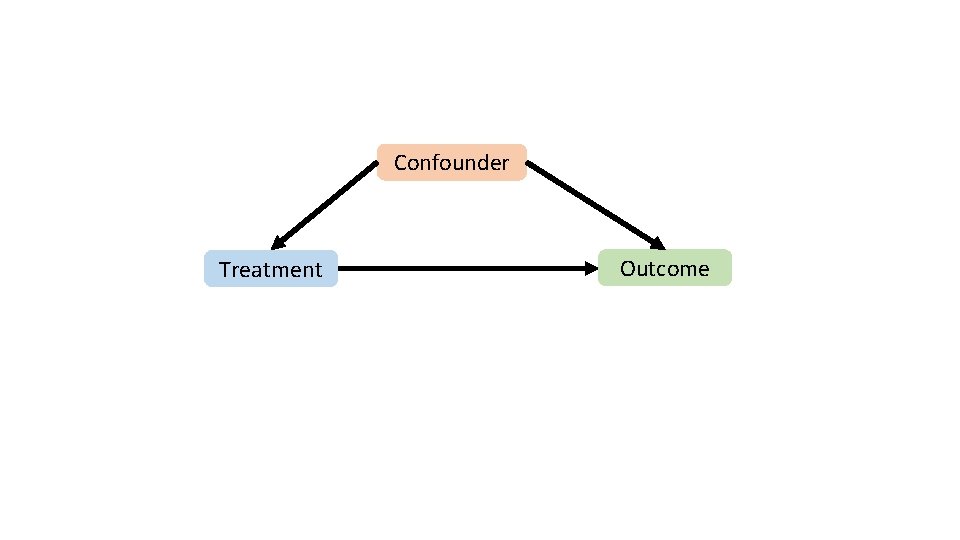
Inverse Probability of Treatment Weights (IPTW) • Goal of IPTW is to control confounding: the systematic differences between exposure groups that are associated with the outcome of interest. Confounder Treatment Outcome
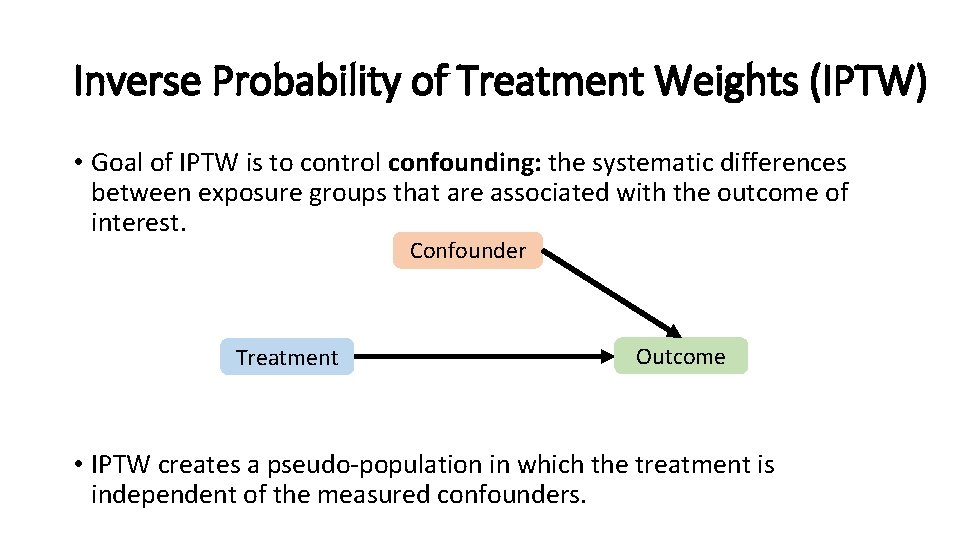
Inverse Probability of Treatment Weights (IPTW) • Goal of IPTW is to control confounding: the systematic differences between exposure groups that are associated with the outcome of interest. Confounder Treatment Outcome • IPTW creates a pseudo-population in which the treatment is independent of the measured confounders.
Slide credit: Alan Brookhart and Steve Cole, EPID 722

Overview of Propensity Scores • The propensity score is the probability of receiving your observed treatment, given the observed confounders. • Propensity scores are estimated using a predictive model of treatment, as a function of the confounders. • For each participant, you use this model to compute a predicted probability of receiving treatment (a. k. a. , the propensity score).

IPTW using Propensity Scores • The propensity score (PS) is used to calculate each participant’s weight: • For treated/exposed patients: weight = 1 / PS • For untreated/unexposed patients: weight = 1 / (1 -PS)

Apply IPTW • Fit a standard regression model for the exposure-outcome relationship, but using the weighted observations. • Estimates the average effect of treatment in the population. • Average risk of outcome if everyone had been treated vs. average risk of outcome if nobody had been treated. • Weights can be stabilized to improve efficiency. • Need to account for weights in estimating standard error.

R Markdown Example • Using the births data, estimate a propensity score model for the probability of receiving early prenatal care as a function of confounders. • Calculate IPTW based on the propensity score model. • Apply IPTW to estimate the weighted association between early prenatal care and preterm birth.

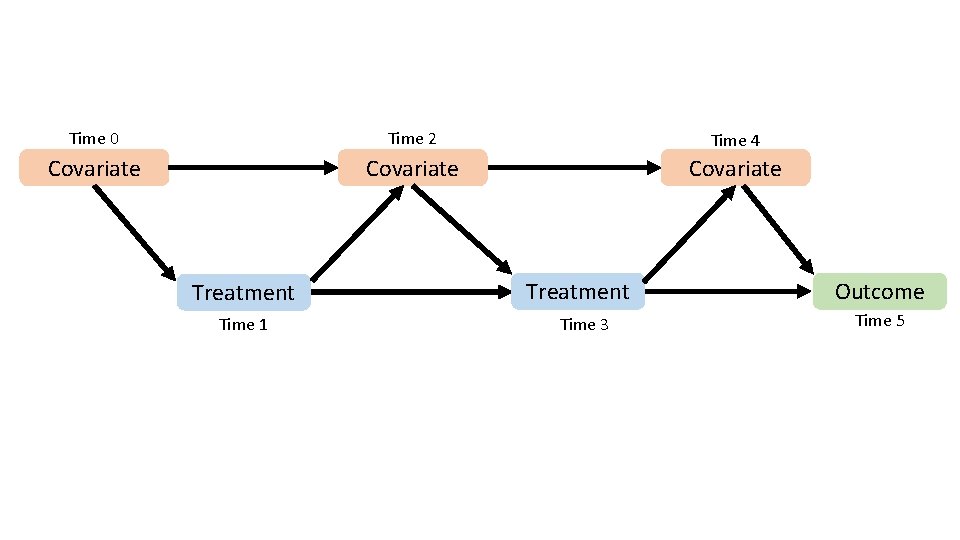
Using IPTW for Marginal Structural Models • Time-varying exposures are often of interest: • Births data: Time-varying attendance of prenatal care visits. • My dissertation: Time-varying depressive symptoms. • Time-varying covariates may be both confounders and intermediates: • Predictors of the exposure and outcome (confounders). • Affected by history of exposure (intermediates).
Confounder Treatment Outcome
Time 0 Time 2 Time 4 Covariate Treatment Time 1 Treatment Time 3 Outcome Time 5

Using IPTW for Marginal Structural Models •

R Markdown Example • Using my dissertation data: 455 HIV-positive people who inject drugs (PWID) in Vietnam, followed for 2 years with study visits every 6 months. • Example analysis: What is the effect of depressive symptoms on injecting risk behaviors? • Use IPTW for marginal structural model, given time-varying exposure and confounders.
- Slides: 25