Inverse Normal Calculations Inverse Normal Calculations Consider a

Inverse Normal Calculations

Inverse Normal Calculations Consider a population of crabs where the length of a shell, X mm, is normally distributed with a mean of 70 mm and a standard deviation of 10 mm. A biologist wants to protect the population by allowing only the largest 5% of crabs to be harvested. He therefore asks the question: “ 95% of the crabs have lengths less than what? ” The biologist needs to find k such that P(X < k) = 0. 95. The number k is known as a quantile, and in this case, the 95% quantile.

Inverse Normal Calculations •

Inverse Normal Calculations Example 1. Consider a population of crabs where the length of a shell, X mm, is normally distributed with a mean of 70 mm and a standard deviation of 10 mm. A biologist wants to protect the population by allowing only the largest 5% of crabs to be harvested. He therefore asks the question: “ 95% of the crabs have lengths less than what? ” inv. Norm(0. 95, 70, 10) = 86. 4485 = 86. 4 mm

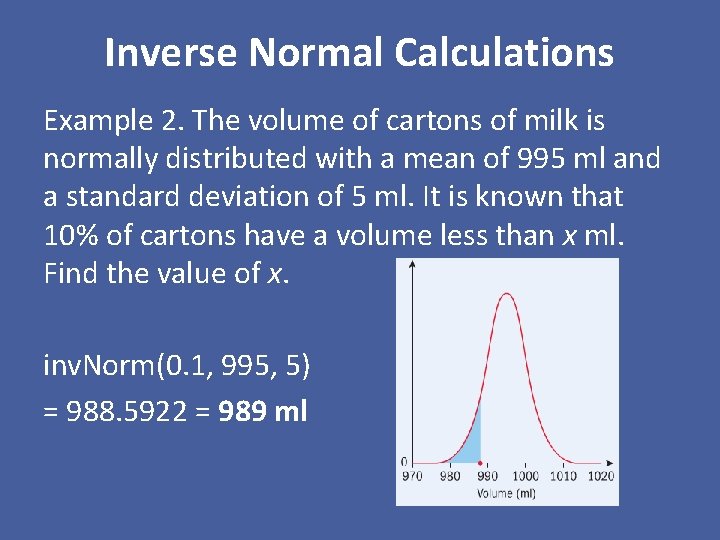
Inverse Normal Calculations Example 2. The volume of cartons of milk is normally distributed with a mean of 995 ml and a standard deviation of 5 ml. It is known that 10% of cartons have a volume less than x ml. Find the value of x. inv. Norm(0. 1, 995, 5) = 988. 5922 = 989 ml

Inverse Normal Calculations To perform inverse normal calculations on the calculator, we must enter the area to the left of k. If P(X > k) = p, then P(X < k) = 1 - p

Inverse Normal Calculations Example 3. A university professor determines that 80% of this year’s history students should pass the final exam. The exam results were approximately normally distributed with a mean of 62 and a standard deviation of 12. Find the lowest score necessary to pass the exam. P(X > k) = 0. 8, which is the same thing as saying P(X < k) = 1 - 0. 8 = 0. 2 inv. Norm(0. 2, 62, 12) = 51. 9005 = 51. 9

Inverse Normal Calculations Example 4. The weights of pears are normally distributed with a mean of 110 g and a standard deviation of 8 g. a. Find the percentage of pears that weighs between 100 g and 130 g. normalcdf(100, 130, 110, 8) = 0. 88814 = 88. 8%

Inverse Normal Calculations Example 4. The weights of pears are normally distributed with a mean of 110 g and a standard deviation of 8 g. b. It is known that 8% of the pears weigh more than m g. Find the value of m. inv. Norm(0. 92, 110, 8) = 121. 2405 = 121 g

Inverse Normal Calculations Example 4. The weights of pears are normally distributed with a mean of 110 g and a standard deviation of 8 g. c. 250 pears are weighed. Calculate the expected number of pears that weigh less than 105 g. normalcdf(-1 E 99, 105, 110, 8) = 0. 265985 = 0. 266 x 250 = 66 or 67 pears (depending on rounding)