Inverse Laplace Transform Laplace Transform of derivatives Laplace

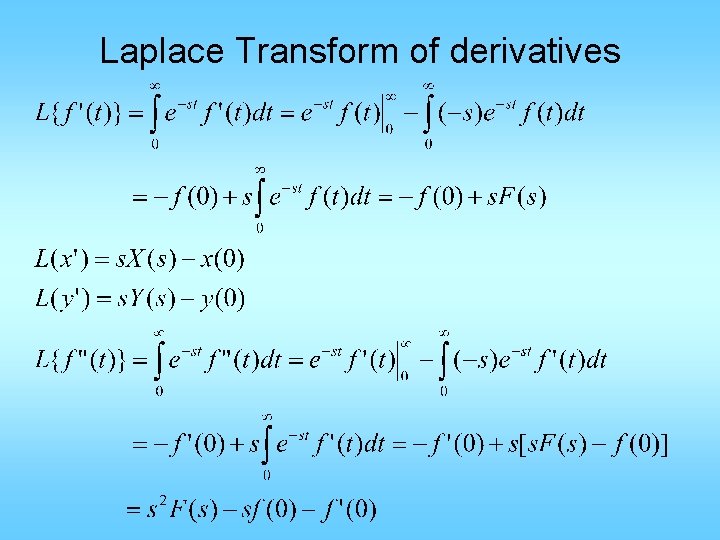


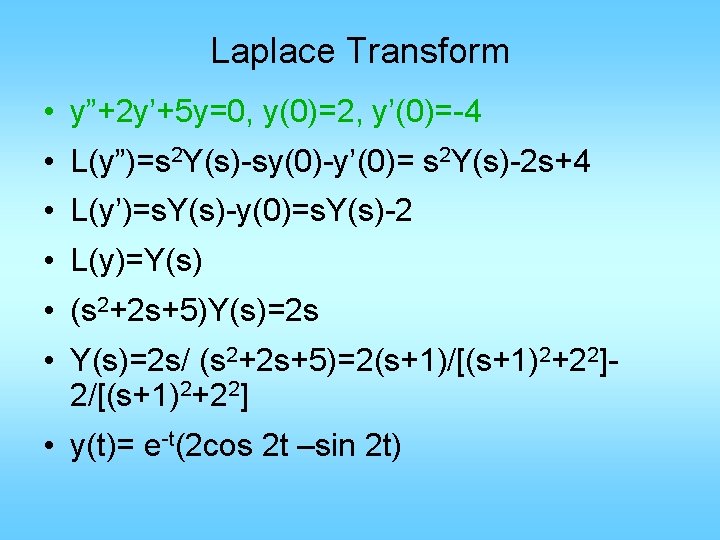
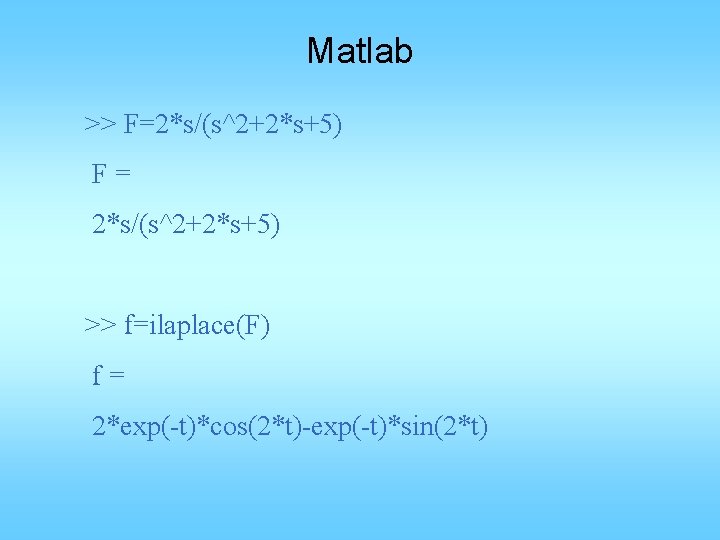
![Y”+2 y’+ y=0, y(0)= 1, y’(0)= -2 >> A=[0 1; -1 -2]; B=[0; 1]; Y”+2 y’+ y=0, y(0)= 1, y’(0)= -2 >> A=[0 1; -1 -2]; B=[0; 1];](https://slidetodoc.com/presentation_image_h2/3cf3b87e72e88acc0f1278672c319a41/image-8.jpg)



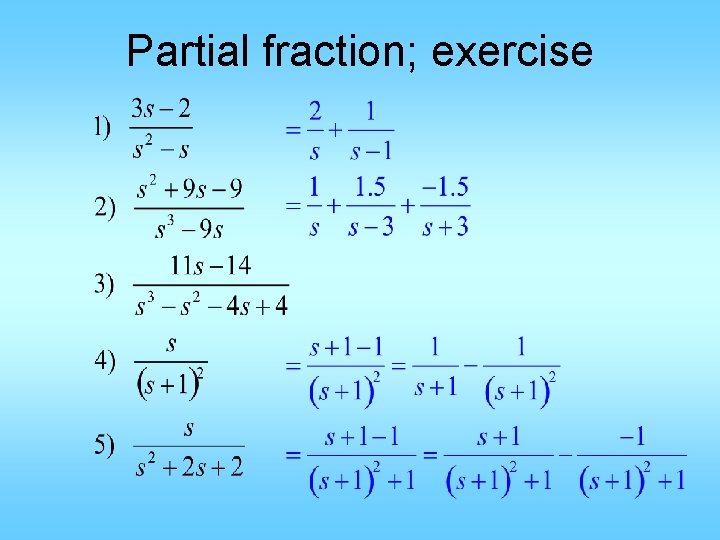
![Matlab >> [r p k]=residue(n, d) >> d=[1 -1 0] r= d= 1 -1 Matlab >> [r p k]=residue(n, d) >> d=[1 -1 0] r= d= 1 -1](https://slidetodoc.com/presentation_image_h2/3cf3b87e72e88acc0f1278672c319a41/image-14.jpg)
![Matlab >> [r p k]=residue(n, d) r= >> n=[1 9 -9] 1. 5000 n= Matlab >> [r p k]=residue(n, d) r= >> n=[1 9 -9] 1. 5000 n=](https://slidetodoc.com/presentation_image_h2/3cf3b87e72e88acc0f1278672c319a41/image-15.jpg)
![Matlab >> [r p k]=residue(n, d) r= >> n=[11 -14] 2. 0000 n= -3. Matlab >> [r p k]=residue(n, d) r= >> n=[11 -14] 2. 0000 n= -3.](https://slidetodoc.com/presentation_image_h2/3cf3b87e72e88acc0f1278672c319a41/image-16.jpg)
![Matlab >> [r p k]=residue(a, b) >> b=[1 2 1] 1 b= 1 2 Matlab >> [r p k]=residue(a, b) >> b=[1 2 1] 1 b= 1 2](https://slidetodoc.com/presentation_image_h2/3cf3b87e72e88acc0f1278672c319a41/image-17.jpg)




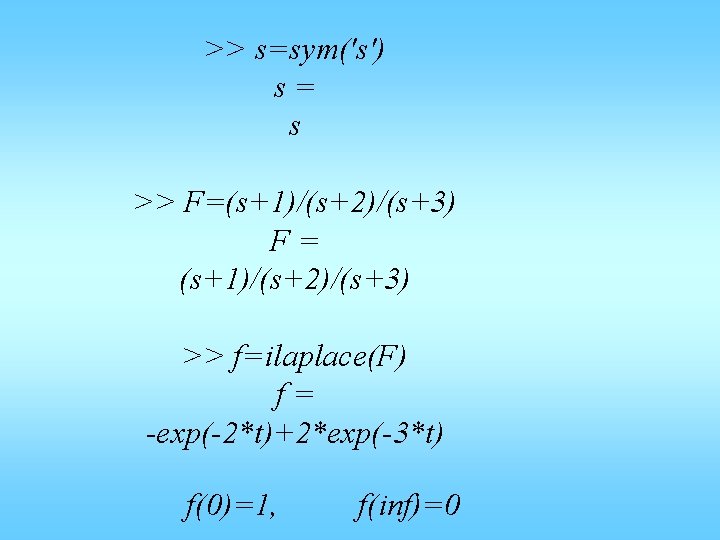













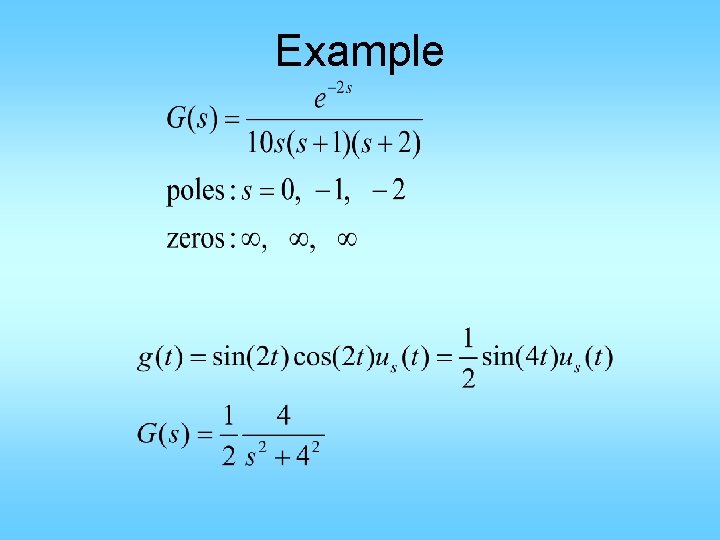



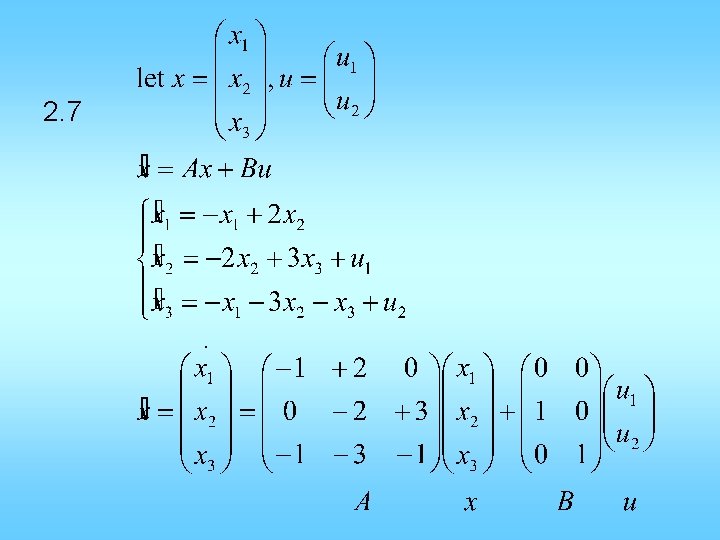
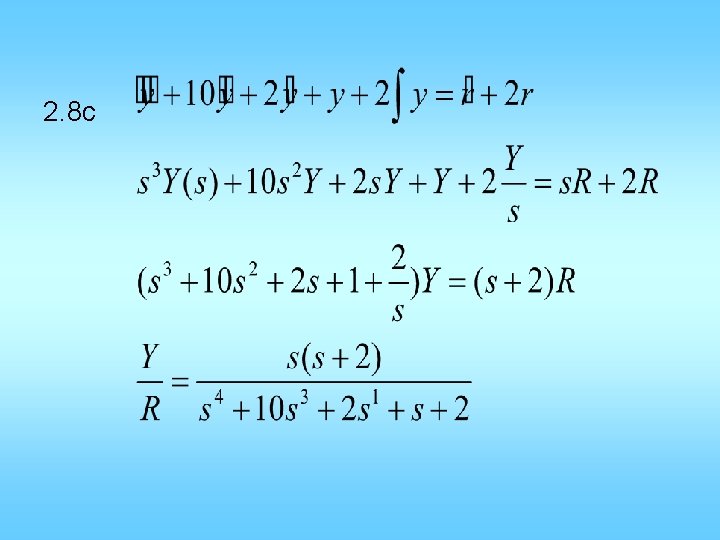
- Slides: 42

Inverse Laplace Transform
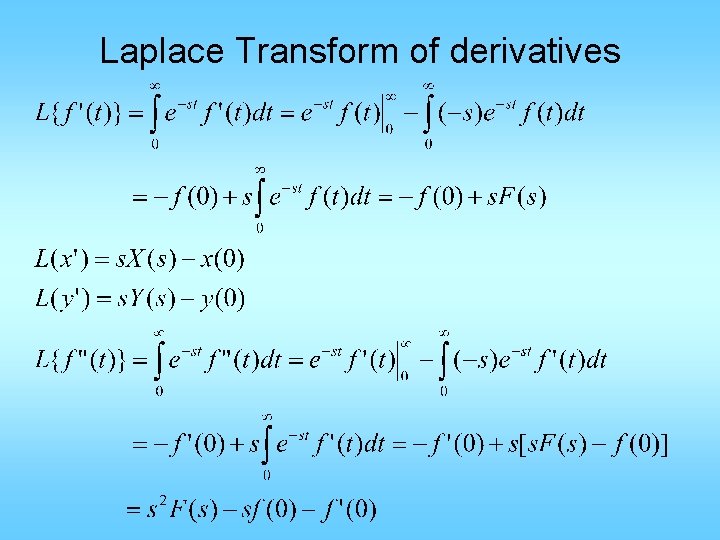
Laplace Transform of derivatives

Laplace Transform applications • y”+9 y=0, y(0)=0, y’(0)=2 • L(y”)=s 2 Y(s)-sy(0)-y’(0)= s 2 Y(s)-2 • L(y)=Y(s) • (s 2+9)Y(s)=2 • Y(s)=2/ (s 2+9) • y(t)=(2/3) sin 3 t

Matlab s=sym('s'); (F=2/(s^2+9) F= 2/(s^2+9) >> f=ilaplace(F) f= 2/9*9^(1/2)*sin(9^(1/2)*t) >> simplify(f) ans = 2/3*sin(3*t)
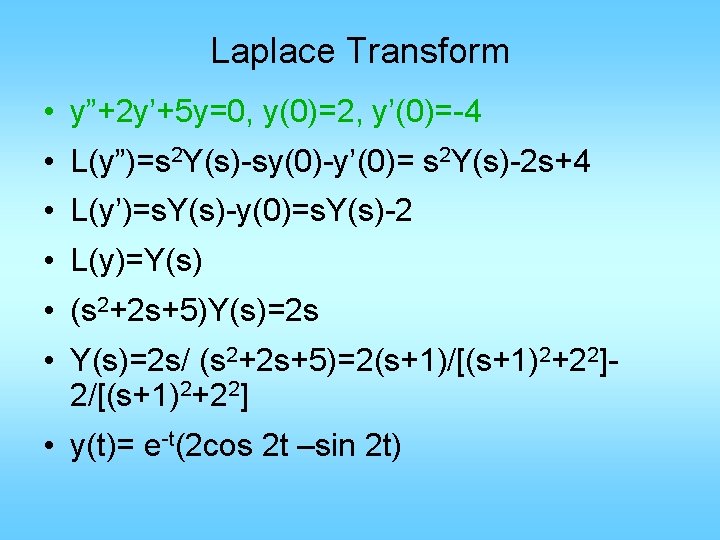
Laplace Transform • y”+2 y’+5 y=0, y(0)=2, y’(0)=-4 • L(y”)=s 2 Y(s)-sy(0)-y’(0)= s 2 Y(s)-2 s+4 • L(y’)=s. Y(s)-y(0)=s. Y(s)-2 • L(y)=Y(s) • (s 2+2 s+5)Y(s)=2 s • Y(s)=2 s/ (s 2+2 s+5)=2(s+1)/[(s+1)2+22]2/[(s+1)2+22] • y(t)= e-t(2 cos 2 t –sin 2 t)
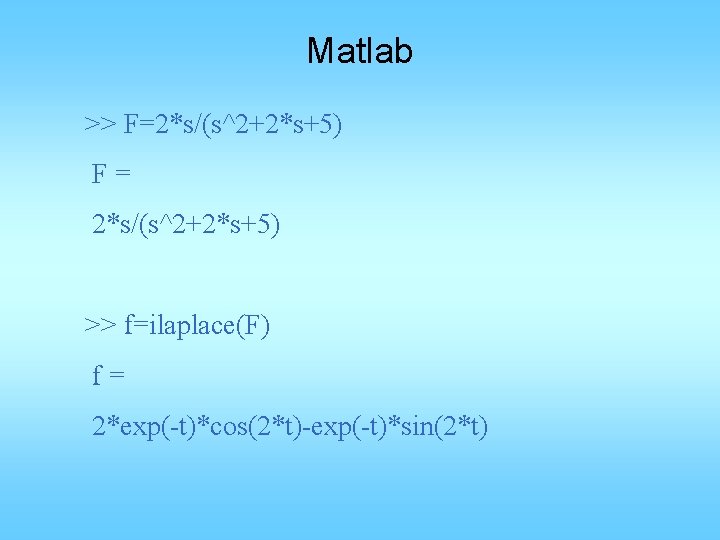
Matlab >> F=2*s/(s^2+2*s+5) F= 2*s/(s^2+2*s+5) >> f=ilaplace(F) f= 2*exp(-t)*cos(2*t)-exp(-t)*sin(2*t)

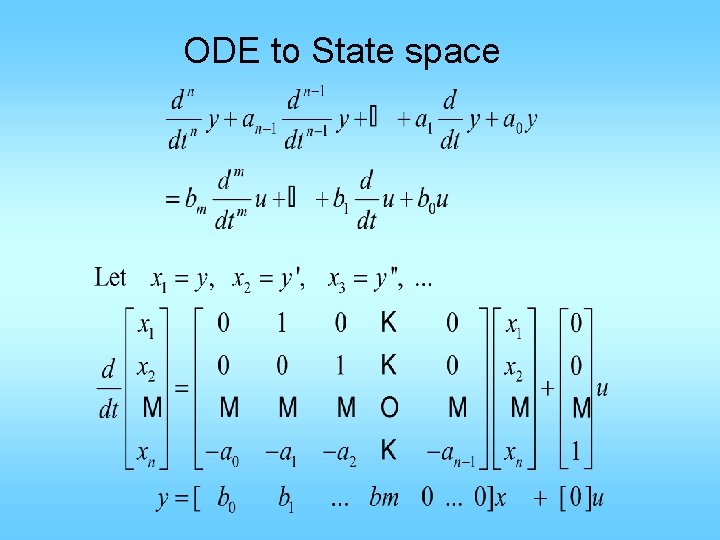
ODE to State space
![Y2 y y0 y0 1 y0 2 A0 1 1 2 B0 1 Y”+2 y’+ y=0, y(0)= 1, y’(0)= -2 >> A=[0 1; -1 -2]; B=[0; 1];](https://slidetodoc.com/presentation_image_h2/3cf3b87e72e88acc0f1278672c319a41/image-8.jpg)
Y”+2 y’+ y=0, y(0)= 1, y’(0)= -2 >> A=[0 1; -1 -2]; B=[0; 1]; C=[1 0]; D=0; >> x 0=[1; -2]; >> t=sym('t'); >> y=C*expm(A*t)*x 0 y = exp(-t)-t*exp(-t) Y”+2 y’+ y=f(t)=u(t), y(0)= 2, y’(0)= 3 >>s=sym('s'); Fs = 1/s; Gs = 1/(s^2+2*s+1) >>x 0=[2; 3]; >> y=C*expm(A*t)*x 0 + ilaplace(Gs*Fs) y = 2*exp(-t)+5*t*exp(-t)+1 -exp(-t)*(t+1)

Partial Fraction

Partial Fraction

Partial fraction; repeated factor

Partial fraction; repeated factor But No FUN
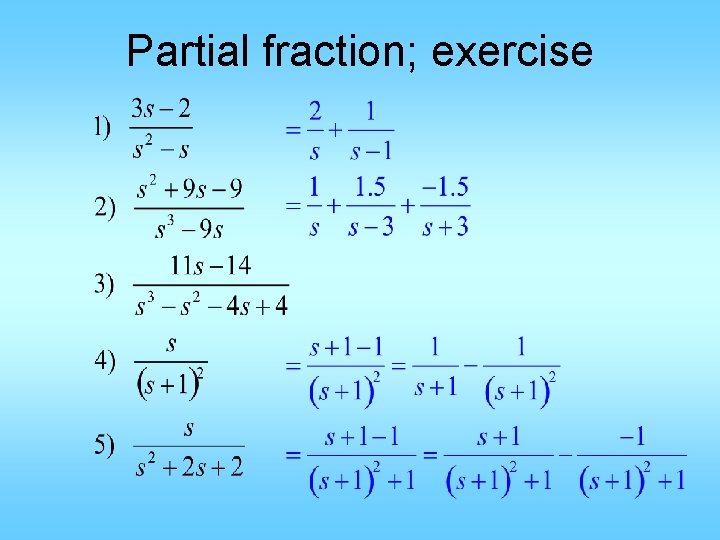
Partial fraction; exercise
![Matlab r p kresiduen d d1 1 0 r d 1 1 Matlab >> [r p k]=residue(n, d) >> d=[1 -1 0] r= d= 1 -1](https://slidetodoc.com/presentation_image_h2/3cf3b87e72e88acc0f1278672c319a41/image-14.jpg)
Matlab >> [r p k]=residue(n, d) >> d=[1 -1 0] r= d= 1 -1 1 0 2 >> n=[3 -2] p= n= 3 1 -2 1/(s-1) + 2/s 0 k= []
![Matlab r p kresiduen d r n1 9 9 1 5000 n Matlab >> [r p k]=residue(n, d) r= >> n=[1 9 -9] 1. 5000 n=](https://slidetodoc.com/presentation_image_h2/3cf3b87e72e88acc0f1278672c319a41/image-15.jpg)
Matlab >> [r p k]=residue(n, d) r= >> n=[1 9 -9] 1. 5000 n= 1 9 -1. 5000 -9 1. 0000 >> d=[1 0 -9 0] p= d= 1 0 -9 0 3 -3 0 k= [] 1. 5/(s-3)1. 5/(s+3)+1/s
![Matlab r p kresiduen d r n11 14 2 0000 n 3 Matlab >> [r p k]=residue(n, d) r= >> n=[11 -14] 2. 0000 n= -3.](https://slidetodoc.com/presentation_image_h2/3cf3b87e72e88acc0f1278672c319a41/image-16.jpg)
Matlab >> [r p k]=residue(n, d) r= >> n=[11 -14] 2. 0000 n= -3. 0000 11 -14 1. 0000 >> d=[1 -1 -4 4] p= d= 1 -1 -4 4 2. 0000 -2. 0000 1. 0000 k= [] 2/(s-2)3/(s+2)+1/(s-1)
![Matlab r p kresiduea b b1 2 1 1 b 1 2 Matlab >> [r p k]=residue(a, b) >> b=[1 2 1] 1 b= 1 2](https://slidetodoc.com/presentation_image_h2/3cf3b87e72e88acc0f1278672c319a41/image-17.jpg)
Matlab >> [r p k]=residue(a, b) >> b=[1 2 1] 1 b= 1 2 >> a=[1 0] 1 -1 p= -1 a= 1 r= 0 -1 k= [] 1/(s+1)2

>> Y=(s^4 -7*s^3+13*s^2+4*s-12)/s^2/(s-3)/(s^2 -3*s+2) Transfer function: s^4 - 7 s^3 + 13 s^2 + 4 s - 12 ------------------s^5 - 6 s^4 + 11 s^3 - 6 s^2 >> [n, d]=tfdata(Y, 'v') n = 0 1 -7 13 4 -12 d = 1 -6 11 -6 0 0 >> [r, p, k]=residue(n, d) r= 0. 5000 -2. 0000 -0. 5000 3. 0000 2. 0000 p= 3. 0000 2. 0000 1. 0000 0 0 k= []

Initial value theorem Conditions: f(t) is continuous except finite jump at t=0 or F(s) is proper: num deg <= den deg

Final value theorem Conditions: f(t) is finite and converges or every pole of s. F(s) has real part < 0

Examples
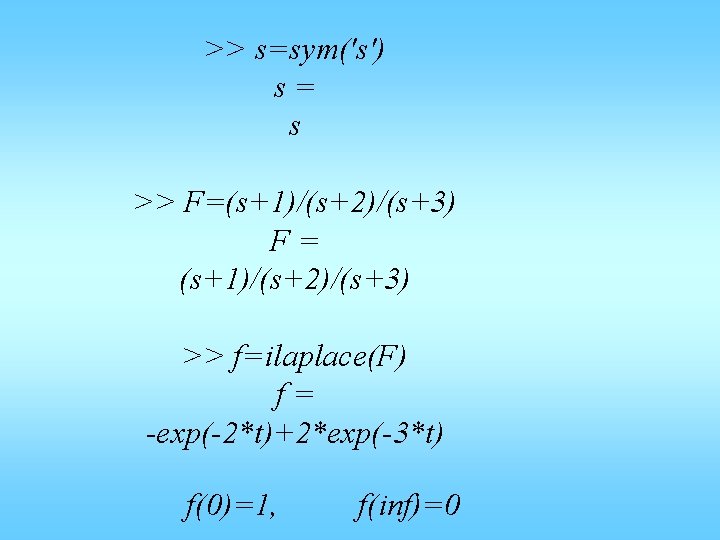
>> s=sym('s') s= s >> F=(s+1)/(s+2)/(s+3) F= (s+1)/(s+2)/(s+3) >> f=ilaplace(F) f= -exp(-2*t)+2*exp(-3*t) f(0)=1, f(inf)=0

Examples

Examples

Transfer Function

Transfer Function

Example

Example A, B, C, D are matrices

Input Output System • Input Output System: Input d(t), u(t) System Output y(t) – If the input x(t) is unit impulse, x(t)=δ (t), the output is called the impulse response. – If the input x(t) is unit step, x(t)=u(t), the output is called the step response.

X(s) H(s) Y(s)

Frequency Response • Frequency Response: Given T. F. H(s)

Example Works only if H(s) is stable

Poles and zeros • Poles: values of s at which TF infinity – Most time, poles = roots of denominator – When there are common factors in numerator and denominator, cancel them first • Zeros: values of s at which TF = 0 – Finite zeros: roots of numerator – Number of zeros at infinity: n-m, n= den deg and m = num deg • Totally n poles and n zeros • n is called the order of the system • n – m the relative order

Example • • • Order: n = 4 = den deg m= num deg = 1 Relative order = n-m = 3 4 poles at: 0, 0, -4, -6 One finite zero at -1 3 zeros at infinity

Stability • System is BIBO stable if any bounded input generates bounded output • Simple criteria: – After common factor cancellation – All poles have strictly negative real parts

Example G 1 is not BIBO stable G 2 and G 3 are
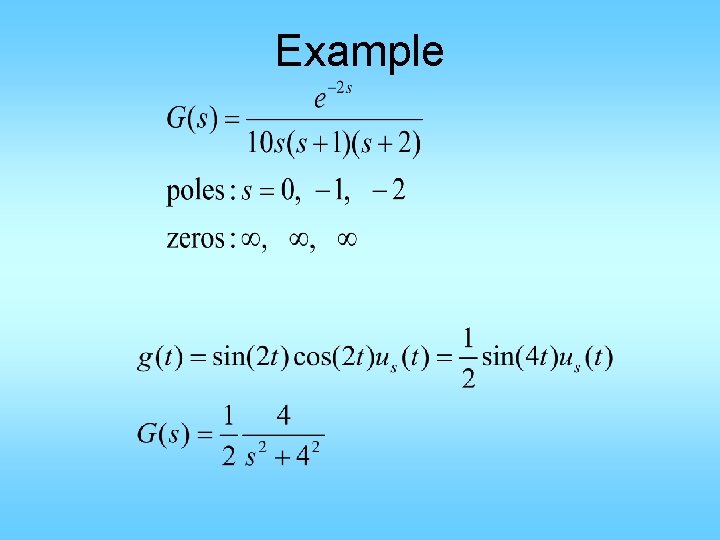
Example

Example

example

>> s=sym('s'); >> Y=1/(s^2+3*s+2)/s*exp(-2*s) Y= 1/(s^2+3*s+2)/s*exp(-2*s) >> ilaplace(Y) ans = 1/2*heaviside(t-2)*(1+exp(-2*t+4)-2*exp(2 -t))
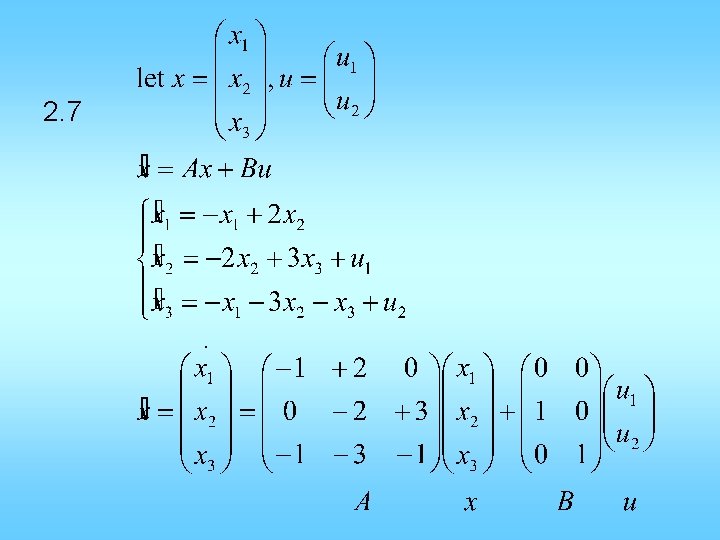
2. 7
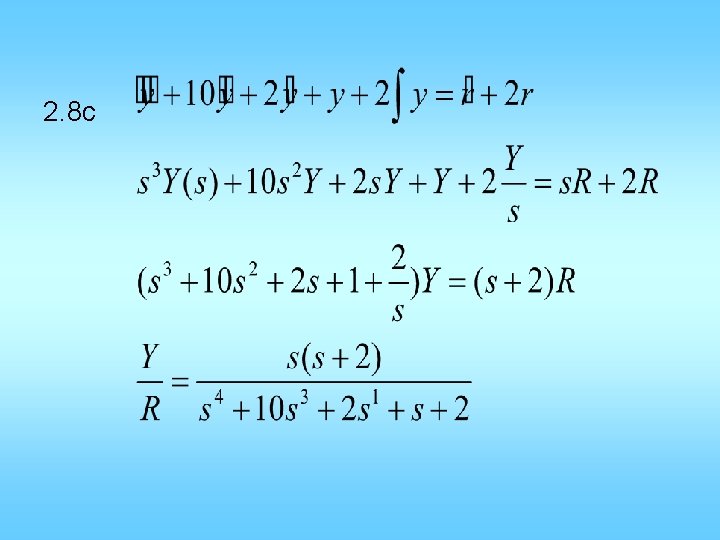
2. 8 c