Inverse Kinematics The Loop Closure Problem in Biology

“Inverse Kinematics” The Loop Closure Problem in Biology Barak Raveh Dan Halperin Course in Structural Bioinformatics Spring 2006

“Riddle” I target

“Riddle” II target

Outline • Introduction – The Loop Closure Problem in Proteins – Direct & Inverse Kinematics • Brief Linear Algebra of a Kinematic Chain • Heuristics: – Cyclic Coordinates Descent Algorithm (“CCD”) • Analytical Solution: – Tripeptide Loop Closure

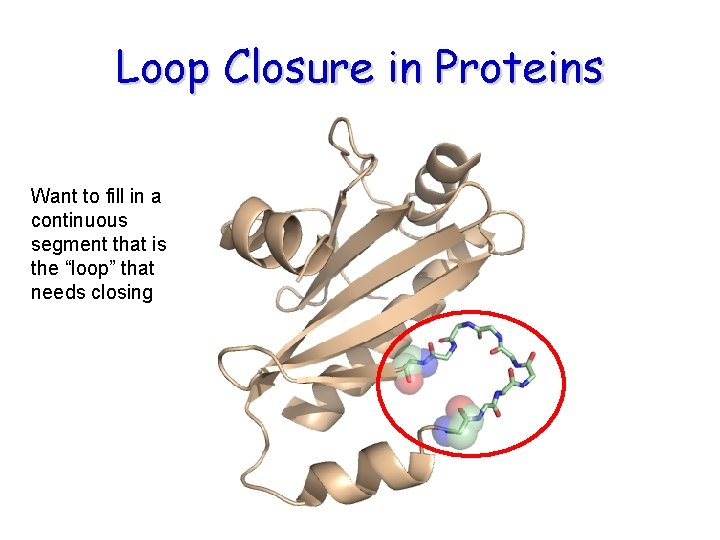
Loop Closure in Proteins Want to fill in a continuous segment that is the “loop” that needs closing

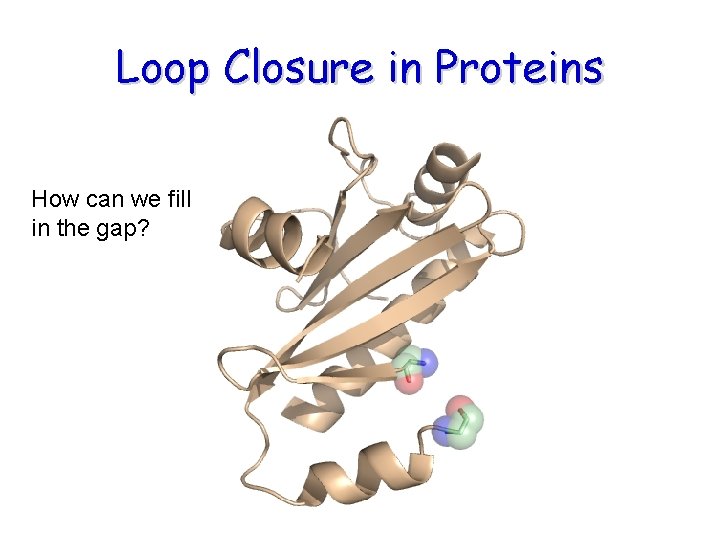
Loop Closure in Proteins How can we fill in the gap?

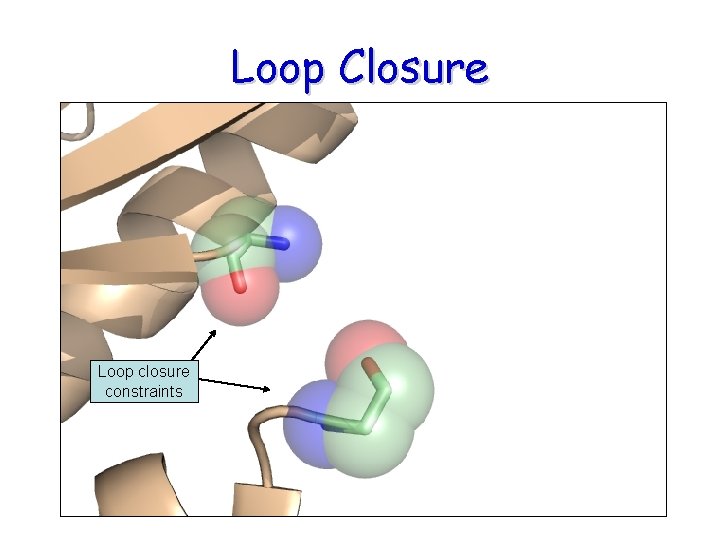
Loop Closure Loop closure constraints

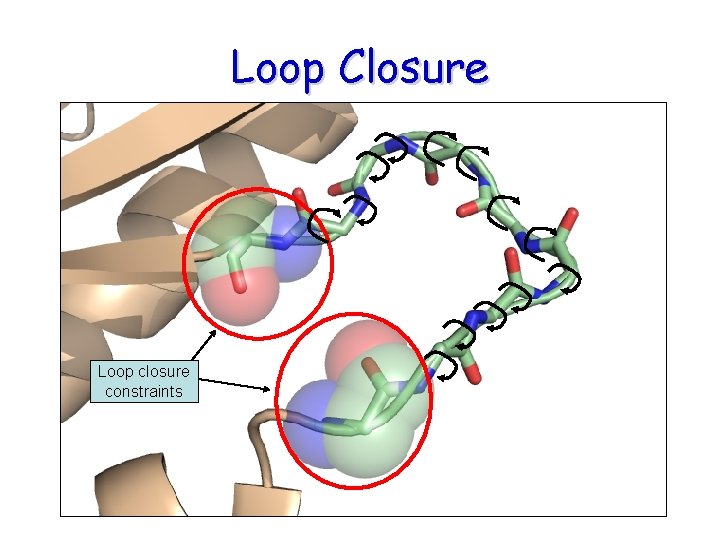
Loop Closure Loop closure constraints

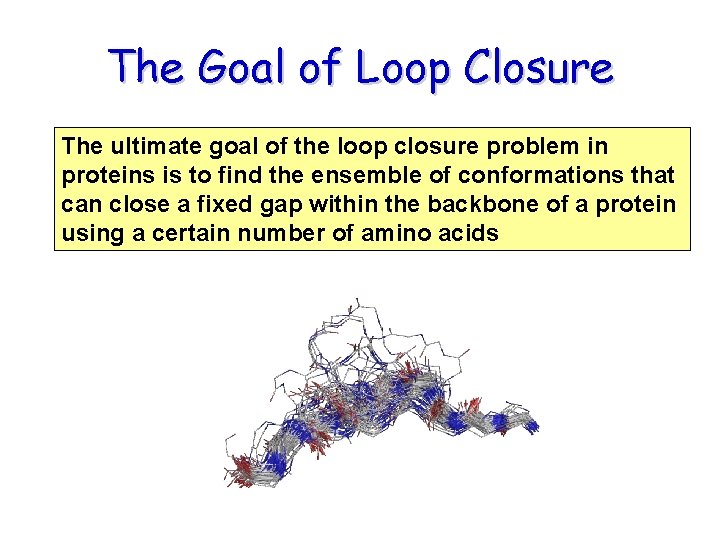
The Goal of Loop Closure The ultimate goal of the loop closure problem in proteins is to find the ensemble of conformations that can close a fixed gap within the backbone of a protein using a certain number of amino acids

Loop Closure – When? • • Protein Loop Design Flexible Docking & Fold Prediction Flexible Peptides And more…

MHC Proteins & Immunology • MHC (Major Histocompatability Proteins) – class I • on the membrane of every cell in our body – class II • On memory cells of immune system • Human MHC = “HLA” (Human Leukocyte Antigens)

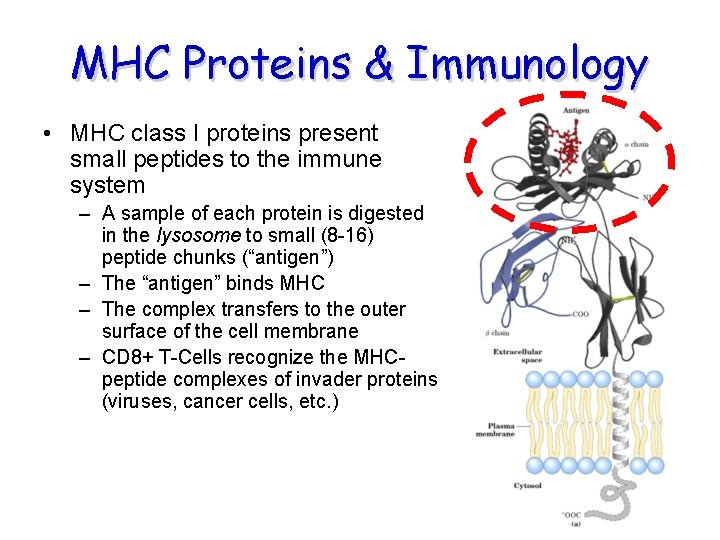
MHC Proteins & Immunology • MHC class I proteins present small peptides to the immune system – A sample of each protein is digested in the lysosome to small (8 -16) peptide chunks (“antigen”) – The “antigen” binds MHC – The complex transfers to the outer surface of the cell membrane – CD 8+ T-Cells recognize the MHCpeptide complexes of invader proteins (viruses, cancer cells, etc. )

MHC I Peptide Binding Domain is Hyper-Variable • 1000 possible alleles in Human MHC (HLA) alone ! • 3 -6 different alleles in each individual • Each allele binds different peptides • Evoloutianary protection of populations • Problems in Organ Transplant

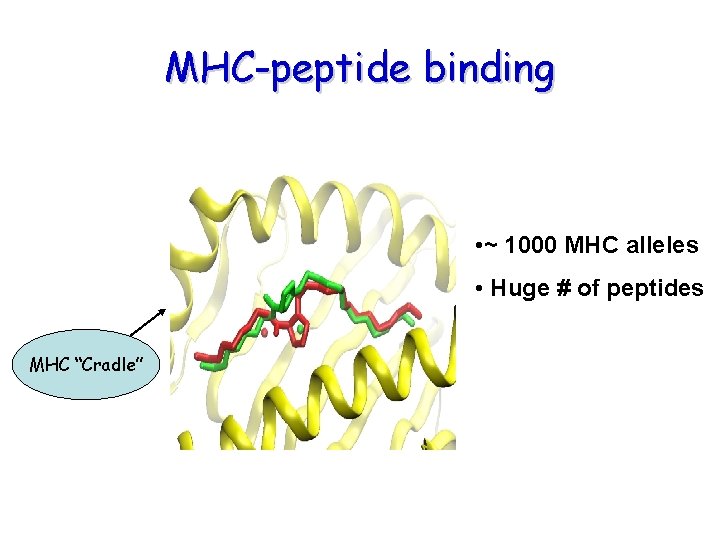
MHC-peptide binding • ~ 1000 MHC alleles • Huge # of peptides MHC “Cradle”

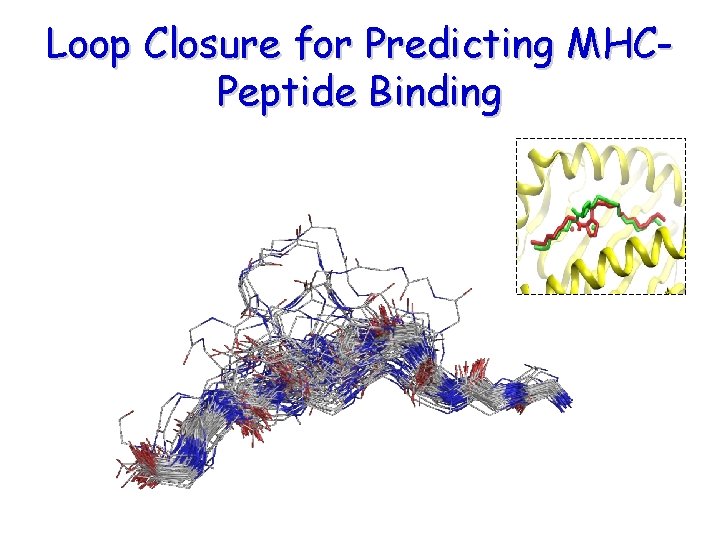
Loop Closure for Predicting MHCPeptide Binding

Outline • Introduction – The Loop Closure Problem in Proteins – Direct & Inverse Kinematics • Brief Linear Algebra of a Kinematic Chain • Heuristics: – Cyclic Coordinates Descent Algorithm (“CCD”) • Analytical Solution: – Tripeptide Loop Closure

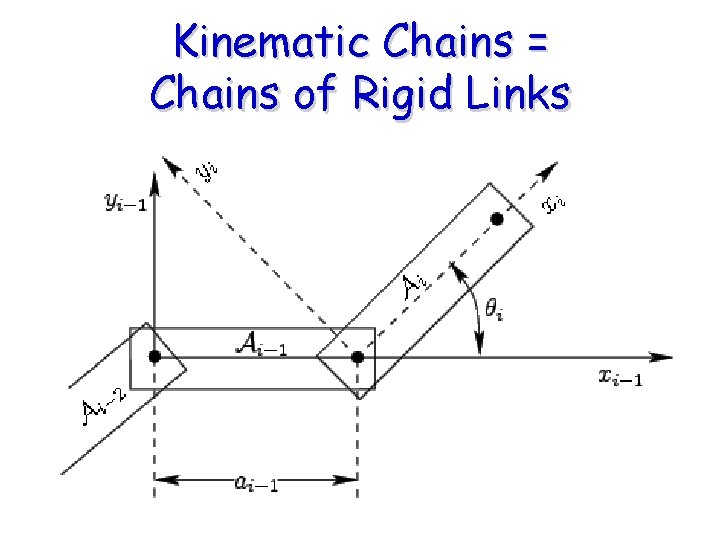
Kinematic Chains = Chains of Rigid Links

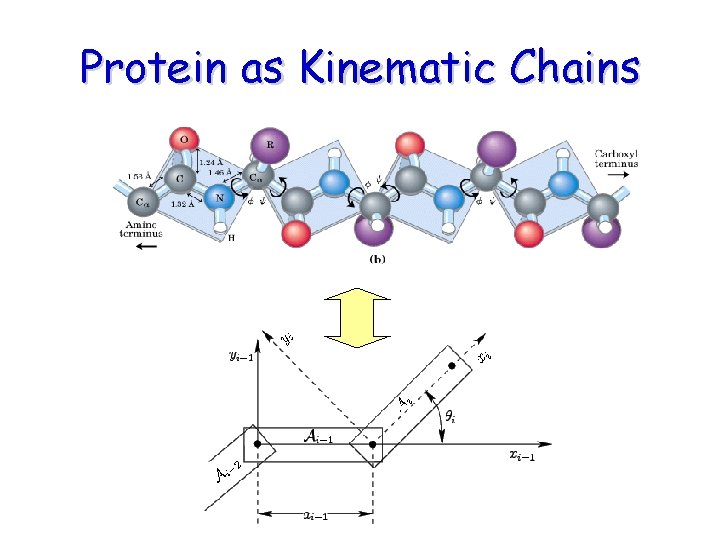
Protein as Kinematic Chains

Direct Kinematics • Where will the robot head move when we change its degrees of freedom? Go right !!! ? ? ?

Inverse Kinematics • How can we move the robot head to a certain location at a certain orientation? Take the ball !!! ? ? ?

Inverse Kinematics in Robots What values of DOFs will bring the robot tool to the desired position and orientation?

Research Questions on Inverse Kinematics • Can we find a single solution to an inverse kinematics problem? • Can we find all solutions to an inverse kinematics problem? • How many solutions exist? – 0? – 1? – Many ? – infinite ?

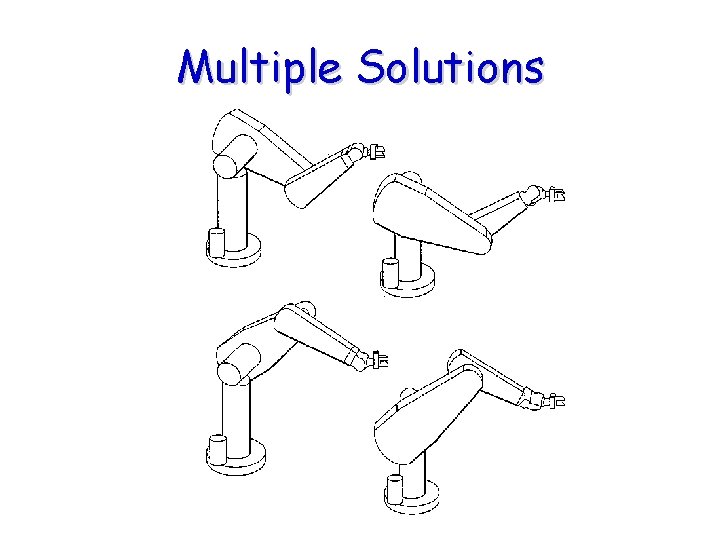
Multiple Solutions

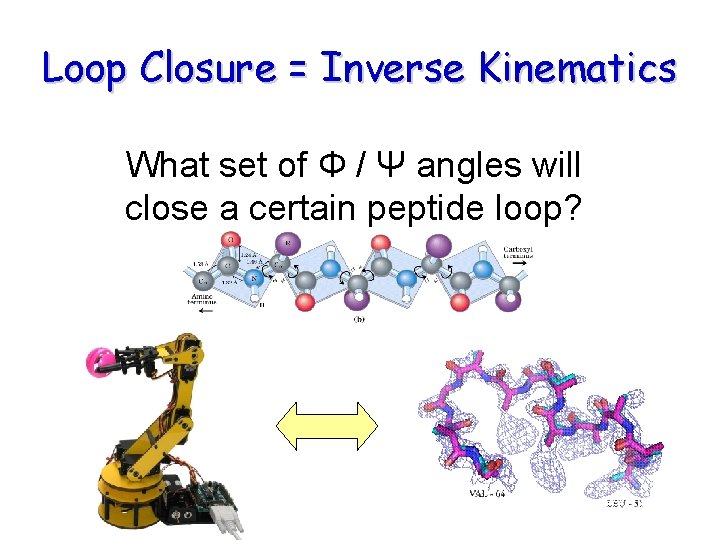
Loop Closure = Inverse Kinematics What set of Φ / Ψ angles will close a certain peptide loop?

Outline • Introduction – The Loop Closure Problem in Proteins – Direct & Inverse Kinematics • Brief Linear Algebra of a Kinematic Chain • Heuristics: – Cyclic Coordinates Descent Algorithm (“CCD”) • Analytical Solution: – Tripeptide Loop Closure

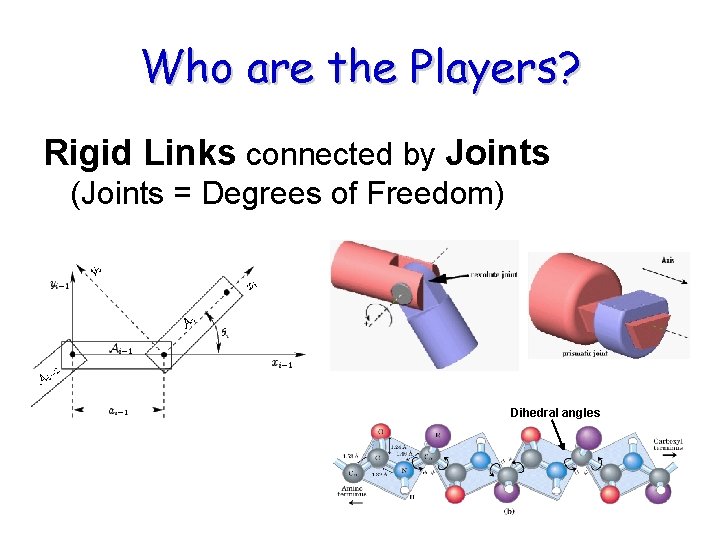
Who are the Players? Rigid Links connected by Joints (Joints = Degrees of Freedom) Dihedral angles

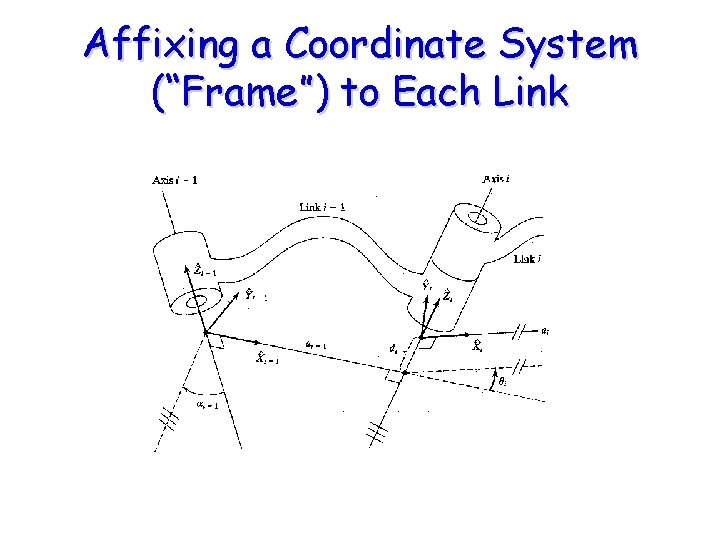
Affixing a Coordinate System (“Frame”) to Each Link

Positions, orientations and frames • The position of a point p relative to a coordinate system A (Ap):

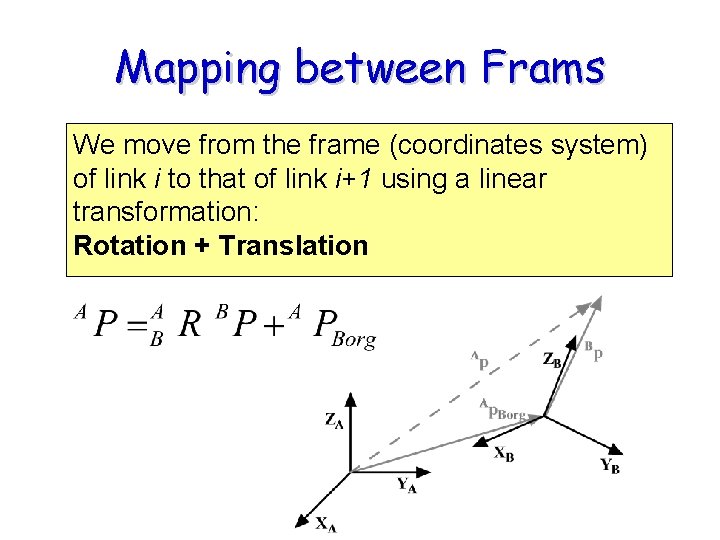
Mapping between Frams We move from the frame (coordinates system) of link i to that of link i+1 using a linear transformation: Rotation + Translation

Examples of Rotation Matrices

“Homogenous Transform”: Translation + Rotation using a single 4 x 4 Matrix

Direct Kinematics • Where will the robot head move when we change its degrees of freedom? Go right !!! ? ? ?

Direct Kinematics = Linear Algebra We can move from the frame (coordinates system) of link i to that of link i+k using straightforward matrix multiplication • Each transform can be written as a combination of a translation and a rotation • The single transformation that relates frame {n} to frame {0}:

2 D Example with Revolute Joints

Inverse Kinematics in Robots What values of DOFs will bring the robot tool to the desired position and orientation? Analytical Solution to Inverse Kinematics = Solving a set of equations on a matrix multiplication system

So what is the problem? Solving the set of equations is usually infeasible! ?

Outline • Introduction – The Loop Closure Problem in Proteins – Direct & Inverse Kinematics • Brief Linear Algebra of a Kinematic Chain • Heuristics: – Cyclic Coordinates Descent Algorithm (“CCD”) • Analytical Solution: – Tripeptide Loop Closure

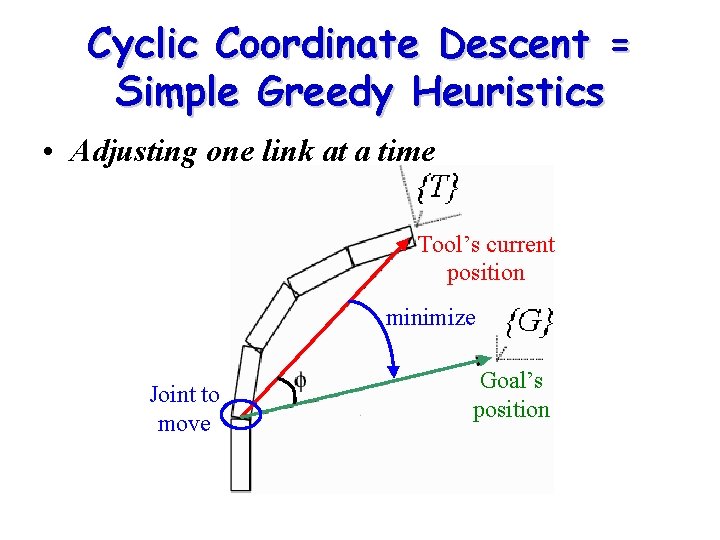
Cyclic Coordinate Descent = Simple Greedy Heuristics • Adjusting one link at a time Tool’s current position minimize Joint to move Goal’s position

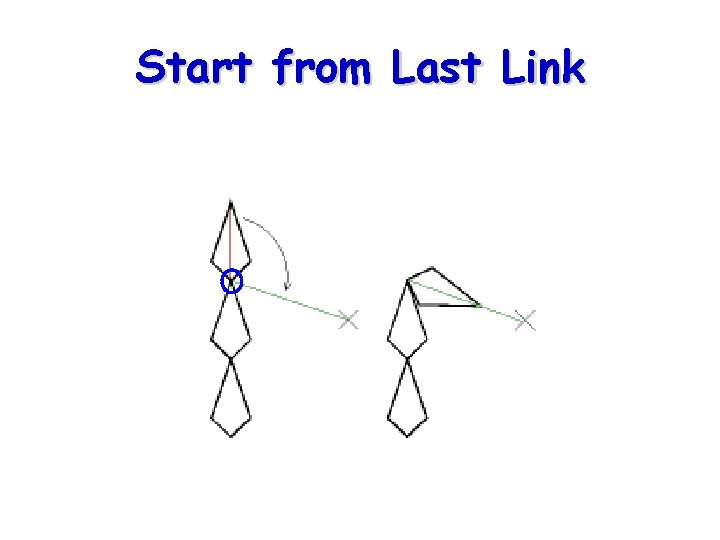
Start from Last Link

Cyclic Coordinate Descent • starts at the last link, adjusting each joint along the way repeat until “satisfied”

Summary of CCD algorithm • While (“not satisfied”) and (# of cycles < maximum): adjust one DOF at a time (iterative) to minimize tool’s distance to the goal, from last link backwards

Cyclic Coordinate Descent Advantages: – – – Allow constraints to be placed (at each step) Free of singularities Independent of DOFs # (degrees of freedom) Extremely fast ! Simple to implement • Disadvantage: – Heuristics • Might not find a solution even if one exists • Does not cover all solutions

CCD for MHC-peptides interaction

Outline • Introduction – The Loop Closure Problem in Proteins – Direct & Inverse Kinematics • Brief Linear Algebra of a Kinematic Chain • Heuristics: – Cyclic Coordinates Descent Algorithm (“CCD”) • Analytical Solution: – Tripeptide Loop Closure – Generalization

“A Kinematic View of Loop Closure” Evangelos A. Coutsias, Chaok Seok, Matthew P. Jacobson, Ken A. Dill

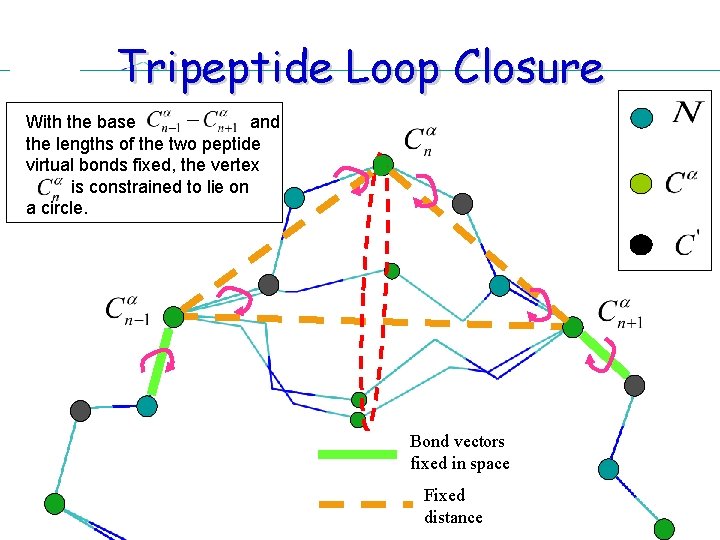
Tripeptide Loop Closure With the base and the lengths of the two peptide virtual bonds fixed, the vertex is constrained to lie on a circle. Bond vectors fixed in space Fixed distance

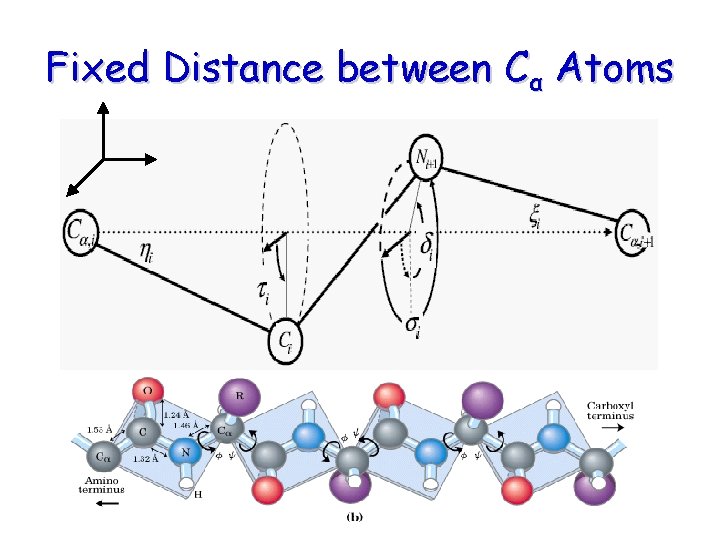
Fixed Distance between Cα Atoms

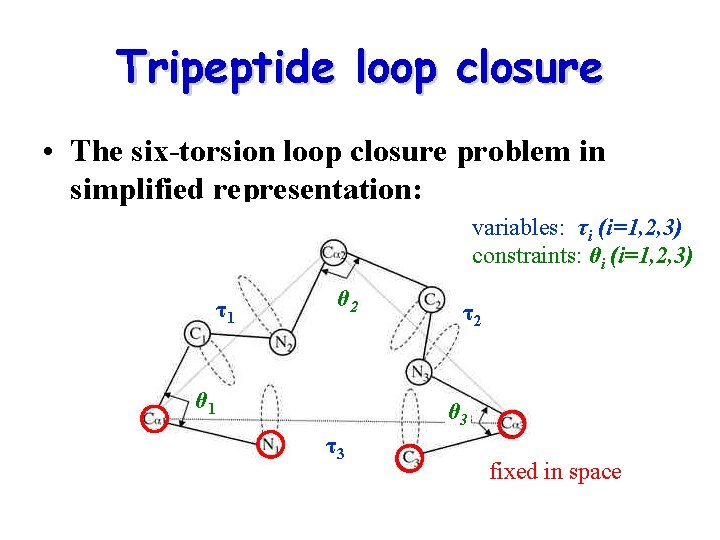
Tripeptide loop closure • The six-torsion loop closure problem in simplified representation: variables: τi (i=1, 2, 3) constraints: θi (i=1, 2, 3) τ1 θ 2 θ 1 τ2 θ 3 τ3 fixed in space

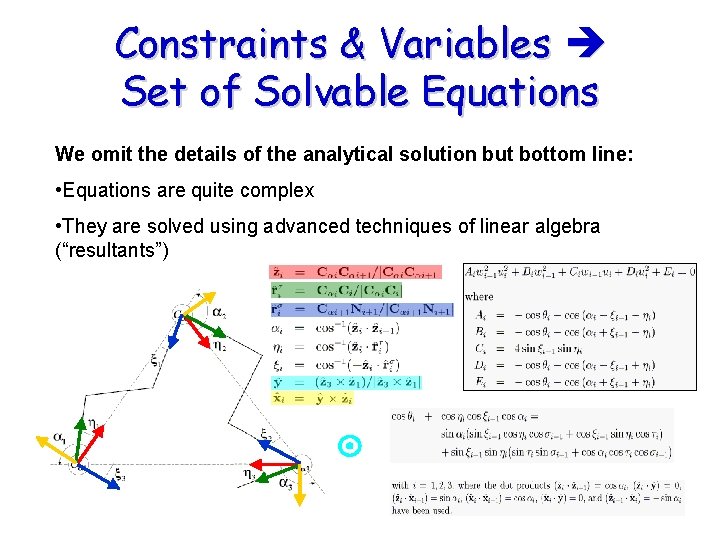
Constraints & Variables Set of Solvable Equations We omit the details of the analytical solution but bottom line: • Equations are quite complex • They are solved using advanced techniques of linear algebra (“resultants”)

Solving the equations • We end up with a degree 16 polynomial • Throretically, there might be up to 16 solutions to this polynomial 16 = Upper bound on number of solutions to each tripeptide loop closure problem • In practice, at most 10 real solutions has been found in the article’s research

Summary • Loop closure of peptides can help in key challenges of computational biology • Analytical Solutions exist only for a very small number of DOFs (Degrees Of Freedom) • Efficient heuristics are not guaranteed to find all solutions, or even a single solution – But they work well in practice

Thank-You !