Inverse Functions Lesson 8 2 Definition A function

Inverse Functions Lesson 8. 2

Definition • A function is a set of ordered pairs with no two first elements alike. § f(x) = { (x, y) : (3, 2), (1, 4), (7, 6), (9, 12) } • But. . . what if we reverse the order of the pairs? § This is also a function. . . it is the inverse function § f -1(x) = { (x, y) : (2, 3), (4, 1), (6, 7), (12, 9) }

Example • Consider an element of an electrical circuit which increases its resistance as a function of temperature. T = Temp R = Resistance -20 50 0 150 20 250 40 350 R = f(T)

Example • We could also take the view that we wish to determine T, temperature as a function of R, resistance. R = Resistance T = Temp 50 -20 150 0 250 20 350 40 T = g(R) Now we would say that g(R) and f(T) are inverse functions

Terminology • If R = f(T). . . resistance is a function of temperature, • Then T = f-1(R). . . temperature is the inverse function of resistance. § f-1(R) is read "f-inverse of R“ § is not an exponent § it does not mean reciprocal

Does This Have An Inverse? • Given the function at the right x Y 1 5 2 9 4 6 7 5 § Can it have an inverse? § Why or Why Not? NO … when we reverse the ordered pairs, the result is Not a function.

Finding the Inverse Try

Composition of Inverse Functions • • Consider f(3) = 27 and f -1(27) = 3 Thus, f(f -1(27)) = 27 and f -1(f(3)) = 3 • In general f(f -1(n)) = n and f -1(f(n)) = n (assuming both f and f -1 are defined for n)

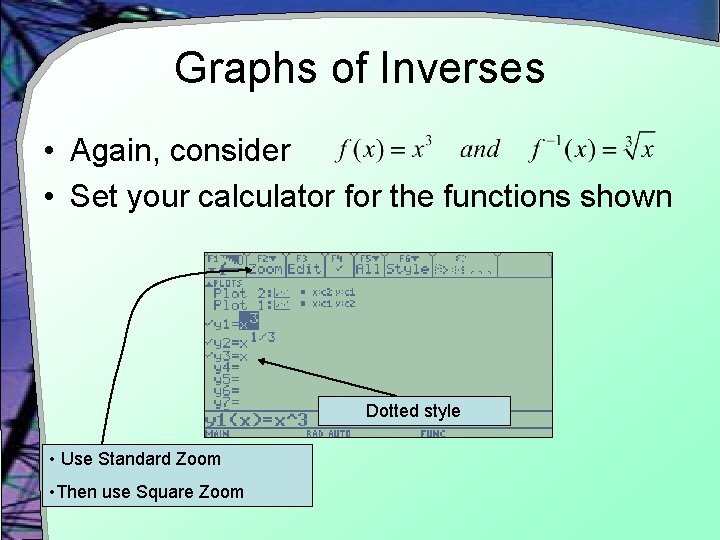
Graphs of Inverses • Again, consider • Set your calculator for the functions shown Dotted style • Use Standard Zoom • Then use Square Zoom

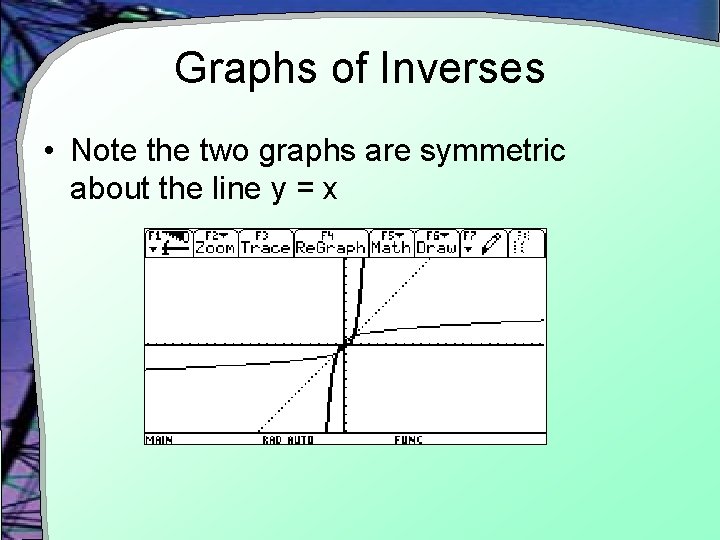
Graphs of Inverses • Note the two graphs are symmetric about the line y = x

Investigating Inverse Functions • Consider • Demonstrate that these are inverse functions • What happens with f(g(x))? Define these functions on your • What happens with g(f(x))? calculator and try them out

Domain and Range • The domain of f is the range of f -1 • The range of f is the domain of f -1 • Thus. . . we may be required to restrict the domain of f so that f -1 is a function

Domain and Range • Consider the function h(x) = x 2 - 9 • Determine the inverse function • Problem => f -1(x) is not a function

Inverse Pumpkins • In a recent pumpkin launching contest, one launcher misfired so that the pumpkin went straight up into the air (!!) and came back down to land on the launch personnel! • Below is the graph of the height of the pumpkin as a function of time h(t) Note. . . the curve is not the path of the pumpkin.

Inverse Pumpkins • What is the "hang time" of the launch? • Restrict the domain of h(t) so that it has an inverse that is a function • Graph the inverse of this function • Change the story to go with your new graph. Explain in your story why it makes sense that the inverse is a function.

Assignment • Lesson 8. 2 • Page 370 • Exercises 1 – 49 EOO