Inventory Models Uncertain Demand The Newsvendor Model Background

Inventory Models Uncertain Demand: The Newsvendor Model

Background: expected value A fruit seller example Undamaged mango Damaged mango Profit $4 $1 Probability 80% 20% What is the expected profit for a stock of 100 mangoes ? 0. 8 x 100 ($4) + 0. 2 x 100 x ($1) = 320 + 20 = $340 random variable: ai probability: pi Expected value = a 1 p 1 + a 2 p 2 + … + ak pk = Si = 1, , k aipi

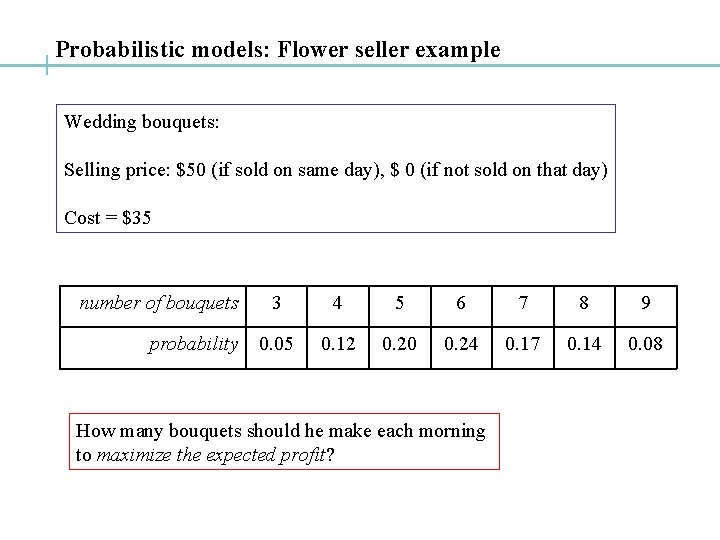
Probabilistic models: Flower seller example Wedding bouquets: Selling price: $50 (if sold on same day), $ 0 (if not sold on that day) Cost = $35 number of bouquets probability 3 4 5 6 7 8 9 0. 05 0. 12 0. 20 0. 24 0. 17 0. 14 0. 08 How many bouquets should he make each morning to maximize the expected profit?

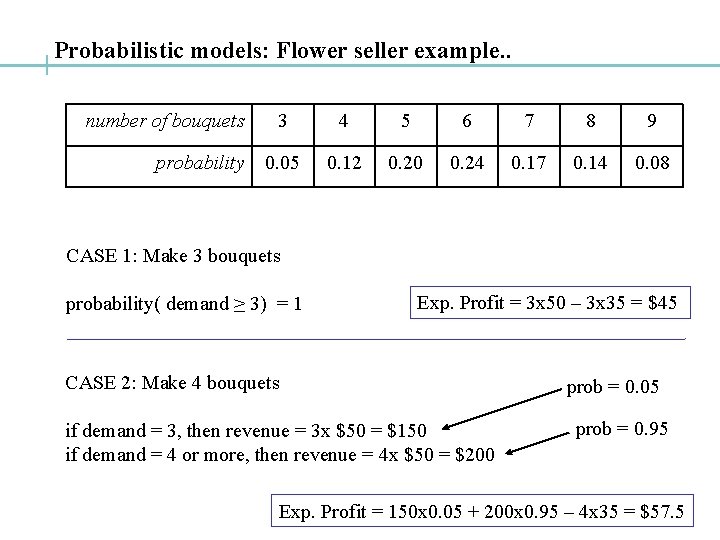
Probabilistic models: Flower seller example. . number of bouquets probability 3 4 5 6 7 8 9 0. 05 0. 12 0. 20 0. 24 0. 17 0. 14 0. 08 CASE 1: Make 3 bouquets probability( demand ≥ 3) = 1 Exp. Profit = 3 x 50 – 3 x 35 = $45 CASE 2: Make 4 bouquets if demand = 3, then revenue = 3 x $50 = $150 if demand = 4 or more, then revenue = 4 x $50 = $200 prob = 0. 05 prob = 0. 95 Exp. Profit = 150 x 0. 05 + 200 x 0. 95 – 4 x 35 = $57. 5

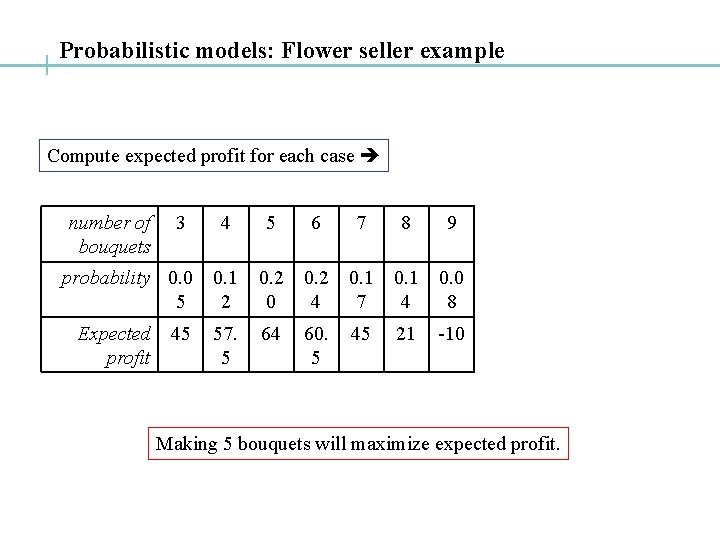
Probabilistic models: Flower seller example Compute expected profit for each case number of bouquets 3 4 5 6 7 8 9 probability 0. 0 5 0. 1 2 0 0. 2 4 0. 1 7 0. 1 4 0. 0 8 Expected 45 profit 57. 5 64 60. 5 45 21 -10 Making 5 bouquets will maximize expected profit.

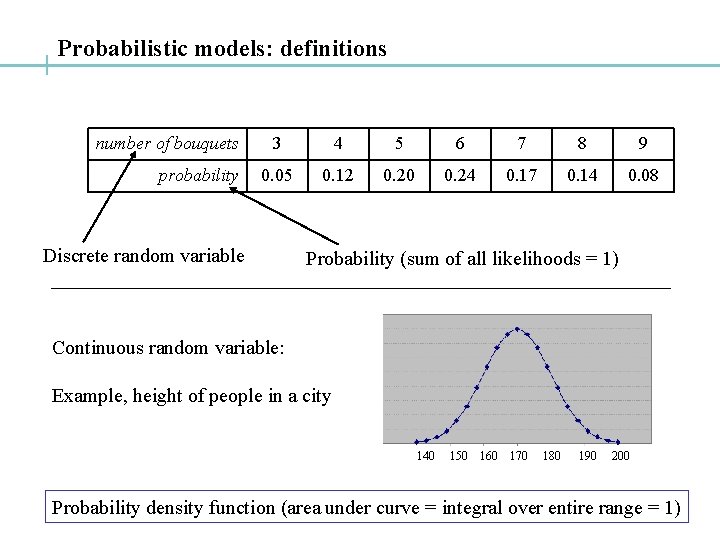
Probabilistic models: definitions number of bouquets probability 3 4 5 6 7 8 9 0. 05 0. 12 0. 20 0. 24 0. 17 0. 14 0. 08 Discrete random variable Probability (sum of all likelihoods = 1) Continuous random variable: Example, height of people in a city 140 150 160 170 180 190 200 Probability density function (area under curve = integral over entire range = 1)

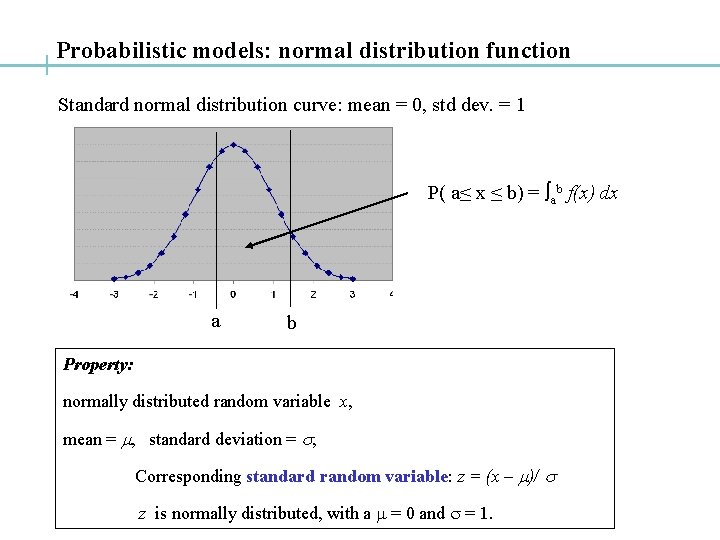
Probabilistic models: normal distribution function Standard normal distribution curve: mean = 0, std dev. = 1 P( a≤ x ≤ b) = ab f(x) dx a b Property: normally distributed random variable x, mean = m, standard deviation = s, Corresponding standard random variable: z = (x – m)/ s z is normally distributed, with a m = 0 and s = 1.

The Newsvendor Model Assumptions: - Plan for single period inventory level - Demand is unknown - p(y) = probability( demand = y), known - Zero setup (ordering) cost

Example: Mrs. Kandell’s Christmas Tree Shop Order for Christmas trees must be placed in Sept Cost per tree: $25 Price per tree: $55 before Dec 25 $15 after Dec 25 If she orders too few, the unit shortage cost is cu = 55 – 25 = $30 If she orders too many, the unit overage cost is co = 25 – 15 = $10 Past Data Sales 22 24 26 28 30 32 34 36 Probability . 05 . 10 . 15 . 20 . 15 . 10 . 05 How many trees should she order?

Stockout and Markdown Risks 1. Mrs. Kandell has only one chance to order until the sales begin: no information to revise the forecast; after the sales start: too late to order more. 2. She has to decide an order quantity Q now D total demand before Christmas F(x) the demand distribution, D > Q stockout, at a cost of: cu (D – Q)+ = cu max{D –Q, 0} D < Q overstock, at a cost of co (Q–D)+ = co max{Q – D, 0}

Key elements of the model 1. Uncertain demand 2. One chance to order (long) before demand 3. ( order > demand OR order < demand) COST

Model development Stockout cost = cu max{D –Q, 0} Overstock cost = co max{Q – D, 0} Total cost = G(Q) = cu (D – Q)+ + co (Q – D)+ Expected cost, E( G(Q) ) = E(cu (D – Q)+ + co (Q – D)+) = cu E(D – Q)+ + co E(Q – D)+

Model Development: generalization Suppose Demand a continuous variable ++ good approximation when number of possibilities is high -- difficult to generate probabilities, but… ++ probability distribution can be guessed

Model solution Minimize g(Q) • g(Q) is a convex function: it has a unique minimum • when g(Q) is at minimum value, F(Q) = cu/(cu + co)

The Critical Ratio Solution to the Newsvendor problem: β = cu /(co + cu ) is called the critical ratio b relative importance of stockout cost vs. markdown cost

Mrs. Kandell’s Problem, solved: cu = 55 – 25 = $30 co = 25 – 15 = $10 Past Data β = cu /(co + cu ) = 30/(30 + 10) = 0. 75 NOTE: optimum ≈ 31 E(D) = 22 x 0. 05 + 24 x 0. 1 + … + 36 x 0. 05 = 29

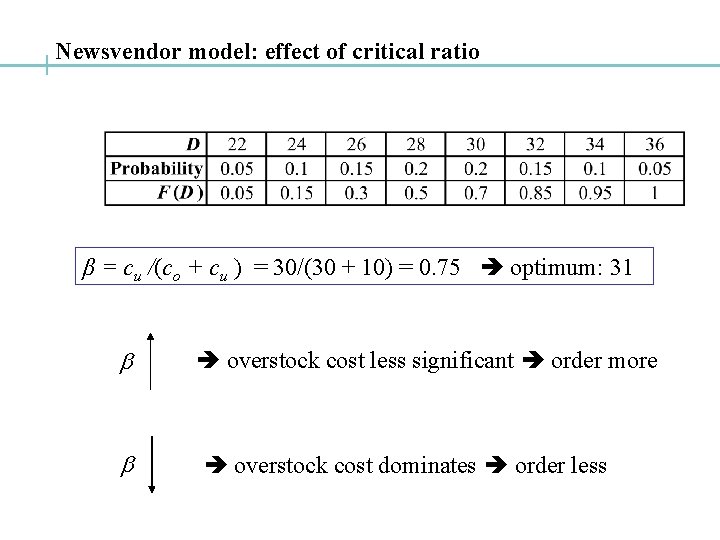
Newsvendor model: effect of critical ratio β = cu /(co + cu ) = 30/(30 + 10) = 0. 75 optimum: 31 b b overstock cost less significant order more overstock cost dominates order less

Summary When demand is uncertain, we minimize expected costs newsvendor model: single period, with over- and under-stock costs Critical ratio determines the optimum order point Critical ratio affects the direction and magnitude of order quantity

Concluding remarks on inventory control Inventory costs lead to success/failure of a company Example: Dell Inc. “Dell's direct model enables us to keep low component inventories that enable us to give customers immediate savings when component prices are reduced, . . . Because of our inventory management, Dell is able to offer some of the newest technologies at low prices while our competitors struggle to sell off older products. ” Drive to reduce inventory costs was main motivation for Supply Chain Management next: Quality Control