Invariance in Property Testing Madhu Sudan MIT Joint

Invariance in Property Testing Madhu Sudan MIT Joint work with Elena Grigorescu & Tali Kaufman. May 1, 2009 UTA: Invariance in Property Testing 1

Property Testing n n Goal: “Efficiently” determine if some “data” “essentially” satisfies some given “property”. Formalism: f : D ! R given as oracle n Data: D ¯nit e, but huge. R ¯nit e, possibly small n Property: Given by F µ f f : D ! Rg o(D ) queries int o f. Even O(1)! n Efficiently: n Must accept if f 2 F Essentially: Ok t o accept if f ¼ g 2 F. May 1, 2009 UTA: Invariance in Property Testing 2

Property Testing n n 6 g(x)] ±(f ; g) = Pr x 2 D [f (x) = Distance: ±(f ; F ) = ming 2 F f ±(f ; g)g f ¼² g if ±(f ; g) · ². Definition: F is (q; ®) locally t est able if 9 a q query t est er t hat accept s f 2 F wit h probability 1 ¡ ² reject s f 2 6 F wit h probability ¸ ® ¢±(f ; F ). n q locally t est able implies 9® > 0 Notes: locally t est able implies 9 q = O(1) May 1, 2009 UTA: Invariance in Property Testing 3

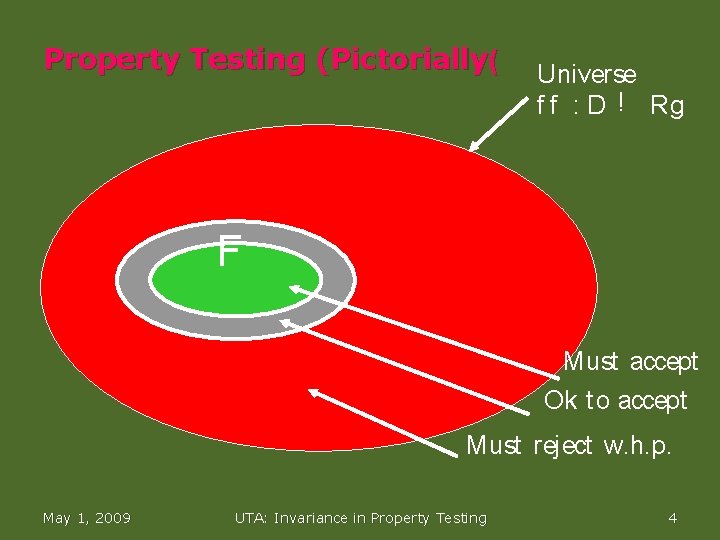
Property Testing (Pictorially( Universe f f : D ! Rg F Must accept Ok t o accept Must reject w. h. p. May 1, 2009 UTA: Invariance in Property Testing 4

Example: Pre-election Polling n Domain = Population f 0; 1 g Range = F = funct ions wit h majority 1 n Property: n Essentially: n Must reject w. h. p. if Pr x 2 D [f (x) = 1] · 1=2 ¡ ² ~ 2 ) queries. Can t est weakly wit h O(1=² Efficiency? Cherno® bounds. May 1, 2009 UTA: Invariance in Property Testing 5

Modern Day Example: Testing Linearity n Vect or space Fn 2 Domain = Field F 2 Range = n F = linear funct ions Property: i. e. , f f (x) = ha; xi ja 2 Fn 2 g n Theorem [Blum, Luby, Rubinfeld ’ 89]: n Pick x; y 2 Fn 2 uniformly. Test: Accept i® f (x) + f (y) = f (x + y) Linearity is 3 locally t est able. May 1, 2009 UTA: Invariance in Property Testing 6

Property Testing: Abbreviated History n n n Prehistoric: Statistical sampling n E. g. , “Majority = 1? ” Linearity Testing [BLR’ 90], Multilinearity Testing [Babai, Fortnow, Lund ’ 91]. Formal Definition: [Rubinfeld S’ 96] Graph/Combinatorial Property Testing [Goldreich, Goldwasser, Ron ’ 96]. n E. g. , Is a graph “close” to being 3 -colorable. Algebraic Testing [GLRSW, RS, FS, AKKLR, KR, JPSZ] n Is multivariate function a polynomial (of bounded degree). Graph Testing [Alon-Shapira, AFNS, Borgs et al. ] n Characterizes graph properties that are testable. May 1, 2009 UTA: Invariance in Property Testing 7

Quest for this talk n n What makes a property testable? In particular for algebraic properties: n Current understanding: n Low-degree multivariate functions are testable. n Different proofs for different cases. n n May 1, 2009 Linear functions Low-degree polynomials F 2 Higher degree polynomials over other fields UTA: Invariance in Property Testing 8

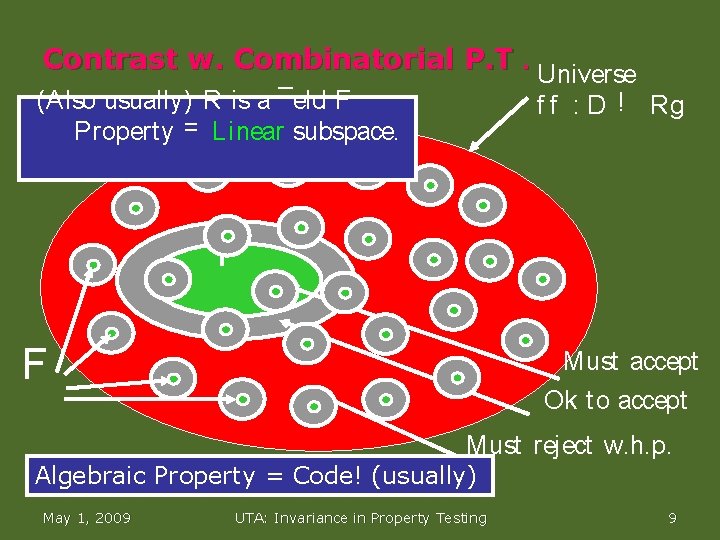
Contrast w. Combinatorial P. T. Universe (Also usually) R is a ¯eld F Property = Linear subspace. f f : D ! Rg F F Must accept Ok t o accept Must reject w. h. p. Algebraic Property = Code! (usually) May 1, 2009 UTA: Invariance in Property Testing 9

Necessary Conditions for Testability n n n One-sided error and testability: ¡ Suppose f is reject ed by a k query 1 sided t est er. Suppose queried point s are x 1 ; : : : ; x k 2 D. Let f (x i ) = ®i. ¡ T hen for every funct ion g 2 F , 6 h® 1 ; : : : ; ®k i. hg(x 1 ); : : : ; g(x k )i = C = hx 1 ; : : : ; x k i ; S ( R k Constraint: g sat is¯es C if hg(x 1 ); : : : ; g(x k )i 2 S F sat is¯es C if every g 2 F sat is¯es C. Conclusion: Testability implies Constraints. May 1, 2009 UTA: Invariance in Property Testing 10

Necessary Conditions for Testability n n n One-sided error and testability: ¡ Suppose f is reject ed by a k query 1 sided t est er. Suppose queried point s are x 1 ; : : : ; x k 2 D. Let f (x i ) = ®i. ¡ T hen for every funct ion g 2 F , 6 h® 1 ; : : : ; ®k i. hg(x 1 ); : : : ; g(x k )i = C = hx 1 ; : : : ; x k i ; S ( R k Constraint: g sat is¯es C if hg(x 1 ); : : : ; g(x k )i 2 S F sat is¯es C if every g 2 F sat is¯es C. Conclusion: Testability implies Constraints. May 1, 2009 UTA: Invariance in Property Testing 11

Constraints, Characterizations, Testing n n n Strong testing: 6 F reject ed Every f 2 by some k local const raint. Set of k local const raint s charact erize F. 9 C 1 ; : : : ; Cm s. t. f 2 F , f sat is¯es Cj for every j. Conclusion: Testability ⇒ Local Characterizations. Example: f µ f Fn 2 ! F 2 g is linear i® for all x; y 2 Fn 2 , f sat is¯es Cx ; y where Cx ; y = hx; y; x + yi ; S = f 000; 011; 101; 110 g. May 1, 2009 UTA: Invariance in Property Testing 12

Characterizations Sufficient? n NO! [Ben-Sasson, Harsha, Raskhodnikova] n Random 3 -locally characterized errorcorrecting codes (“Expander Codes”) are not o(D)-locally testable. n Property: D = [n]; R = f 0; 1 g; F = set of funct ions t hat sat isfy some random 3 ary F 2 linear const raint s. n n Criticism: Random constraints too “asymmetric”. Perhaps should consider more “symmetric” properties. May 1, 2009 UTA: Invariance in Property Testing 13

Invariance & Property testing n n Invariances (Automorphism groups): For permut at ion ¼: D ! D , F is ¼ invariant if f 2 F implies f ± ¼ 2 F. Aut (F ) = f ¼ j F is ¼ invariant g Forms group under composit ion. Hope: If Automorphism group is “large” (or “nice”), then property is testable. May 1, 2009 UTA: Invariance in Property Testing 14

Examples n Majority: ¡ Aut group = SD (full group). ¡ Easy Fact : If Aut (F ) = SD t hen F is poly(R; 1=²) locally t est able. n Graph Properties: ¡ Aut. group given by renaming of vert ices ¡ [AFNS, Borgs et al. ] implies regular propert ies wit h t his Aut group are t est able. n n Statistical Properties: Closed under every permutation of domain and range. Algebraic Properties: What symmetries do they have? Will focus on this today. May 1, 2009 UTA: Invariance in Property Testing 15

Algebraic Properties & Invariances n Properties: D = Fn , R = F (Linearity, Low degree, Reed Muller) Or D = K ¶ F, R = F (Dual BCH) (K ; F ¯nit e ¯elds) n Automorphism groups? n (Linear-Invariant) Additional restriction: Linearity n Linear t ransformat ions of domain. ¼(x) = Ax where A 2 Fn £ n f ; g 2 F and ®; ¯ 2 F implies ®f + ¯g 2 F Question: Are Linear, Linear-Invariant, Locally Characterized Properties Testable? May 1, 2009 UTA: Invariance in Property Testing 16

Linear-Invariance & Testability n Question: Are Linear, Linear-Invariant, Locally Characterized Properties Testable? n Why? n Unifies previous results on Prop. Testing. n (Will show it also is non-trivial extension) n Nice family of 2 -transitive group of symmetries. n Conjecture [Alon, Kaufman, Krivelevich, Litsyn, Ron] : Linear code with k-local constraint and 2 transitive group of symmetries must be testable. May 1, 2009 UTA: Invariance in Property Testing 17

Our Results n n n F µ f K n ! Fg linear, linear invariant , Theorem 1: k locally charact erized implies F is f (K ; k) locally t est able. F µ f K n ! Fg linear, a± ne invariant , Theorem 2: has k local constraint implies F is f (K ; k) locally t est able. Other stuff: n Study of Linear-invariant Properties. n Counterexample to AKKLR conjecture. May 1, 2009 UTA: Invariance in Property Testing 18

Linear Invariant Properties May 1, 2009 UTA: Invariance in Property Testing 19

Examples of Linear-Invariant Families ¡ Polynomials in F[x 1 ; : : : ; x n ] of degree at most d ¡ Traces of Poly in K [x 1 ; : : : ; x n ] of degree at most d ¡ (Traces of ) Homogenous polynomials of degree d ¡ F 1 + F 2 , where F 1 , F 2 are linear invariant. Polynomials support ed by degree 2; 3; 5; 7 monomials. May 1, 2009 UTA: Invariance in Property Testing 20

What Dictates Locality of Characterizations? ¡ Precise locality not yet underst ood: Depends on p ary represent at ion of degrees. Example: F support ed by monomials x pi + pj behaves like degree two polynomial ¡ For a± ne invariant family dict at ed (coarsely) by highest degree monomial in family ¡ For some linear invariant families, can be much less t han t he highest degree monomial. Example: K = F 7 ; F = F 1 + F 2 F 1 = poly of degree at most 16 F 2 = poly support ed on monomials of degree 3 mod 6. Degree(F ) = (n); Locality(F ) · 49. May 1, 2009 UTA: Invariance in Property Testing 21

Analysis Ingredients n Monomial Extraction: n Monomial Spread: E. g. , xy 2 + xyz + x 4 2 F implies xyz 2 F x 5 2 F implies x 4 y; x 3 y 2 also in F (if char(F) large) Su± ces for a± ne invariant families. For linear invariant families, need t o de¯ne t he right paramet er and bound locality weakly in t erms of it. May 1, 2009 UTA: Invariance in Property Testing 22

Local Testing May 1, 2009 UTA: Invariance in Property Testing 23

Key Notion: Single Orbit Property ¡ F has single orbit property if 9 a single const raint C = (hx 1 ; : : : ; x k i ; S) such t hat f C ± ¼g¼ 2 A ut ( F ) charact erize F. ¡ Single orbit property applies t o all known algebraic propert ies, possibly wit h t he except ion of BCH codes. T heorem: Every linear invariant F wit h a k local charact erizat ion, has t he single orbit property under some f (k; K ) local const raint T heorem: If F has single orbit property wit h a k local const raint (wit h some rest rict ions) t hen it is k locally t est able. May 1, 2009 UTA: Invariance in Property Testing 24

BLR (and our) analysis May 1, 2009 UTA: Invariance in Property Testing 25

The tests n Pick x; y 2 R Fn and check BLR: f (x) + f (y) = f (x + y) Need t o show: 9 g s. t. ±(f ; g) · C ¢Pr x ; y [f (x) + f (y) = 6 f (x + y)] n Ours: F given by x 1 ; : : : ; x k ; V Pick linear/ a± ne L : K n ! K n at random Verify hf (L (x 1 )); : : : ; f (L (x k ))i 2 V Need t o show 9 g 2 F s. t. 2 V ±(f ; g) · C ¢Pr L [hf (L (x 1 )); : : : ; f (L (x k ))i 6 May 1, 2009 UTA: Invariance in Property Testing 26

BLR Analysis: Outline ² Have f s. t. Pr x ; y [f (x) + f (y) = 6 f (x + y)] = ± < 1=20. Want t o show f close t o some g 2 F. ² De¯ne g(x) = most likely f f (x + y) ¡ f (y)g. y ² If f close t o F t hen g will be in F and close t o f. ² But if f not close? g may not even be uniquely de¯ned! ² St eps: ¡ St ep 0: Prove f close t o g ¡ St ep 1: Prove most likely is overwhelming majority. ¡ St ep 2: Prove t hat g is in F. May 1, 2009 UTA: Invariance in Property Testing 27

BLR Analysis: Step 0 ² De¯ne g(x) = most likely y f f (x + y) ¡ f (y)g. = g(x)] · 2± Claim: Pr x [f (x) 6 = f (x + y) ¡ f (y)] ¸ ¡ Let B = f xj Pr y [f (x) 6 ¡ Pr x ; y [linearity t est reject s jx 2 B ] ¸ 1 g 2 1 2 ) Pr x [x 2 B ] · 2± ¡ If x 2 6 B t hen f (x) = g(x) May 1, 2009 UTA: Invariance in Property Testing 28

Vot ex (y) BLR Analysis: Step 1 ² De¯ne g(x) = most likely y f f (x + y) ¡ f (y)g. ² Suppose for some x, 9 two equally likely values. Presumably, only one leads t o linear x, so which one? ² If we wish t o show g linear, t hen need t o rule out t his case. Lemma: 8 x, Pr y ; z [Vot ex (y) = 6 Vot ex (z))] · 4± May 1, 2009 UTA: Invariance in Property Testing 29

Vot ex (y) BLR Analysis: Step 1 ² De¯ne g(x) = most likely y f f (x + y) ¡ f (y)g. ² Suppose for some x, 9 two equally likely values. Presumably, only one leads t o linear x, so which one? ² If we wish t o show g linear, t hen need t o rule out t his case. Lemma: 8 x, Pr y ; z [Vot ex (y) = 6 Vot ex (z))] · 4± May 1, 2009 UTA: Invariance in Property Testing 30

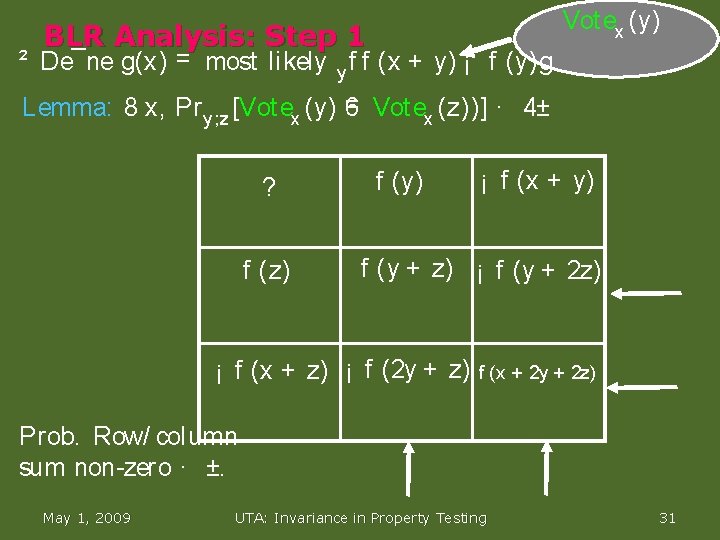
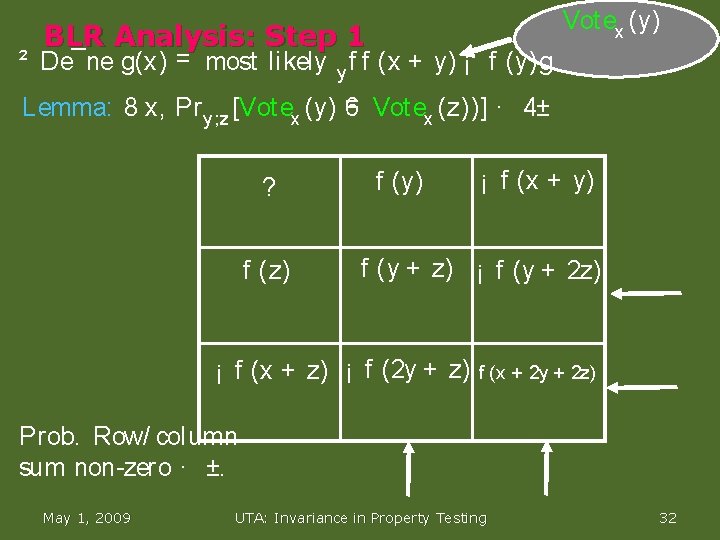
Vot ex (y) BLR Analysis: Step 1 ² De¯ne g(x) = most likely y f f (x + y) ¡ f (y)g. = Vot ex (z))] · 4± Lemma: 8 x, Pr y ; z [Vot ex (y) 6 ? f (z) f (y) ¡ f (x + y) f (y + z) ¡ f (y + 2 z) ¡ f (x + z) ¡ f (2 y + z) f (x + 2 y + 2 z) Prob. Row/ column sum non zero · ±. May 1, 2009 UTA: Invariance in Property Testing 31

Vot ex (y) BLR Analysis: Step 1 ² De¯ne g(x) = most likely y f f (x + y) ¡ f (y)g. = Vot ex (z))] · 4± Lemma: 8 x, Pr y ; z [Vot ex (y) 6 ? f (z) f (y) ¡ f (x + y) f (y + z) ¡ f (y + 2 z) ¡ f (x + z) ¡ f (2 y + z) f (x + 2 y + 2 z) Prob. Row/ column sum non zero · ±. May 1, 2009 UTA: Invariance in Property Testing 32

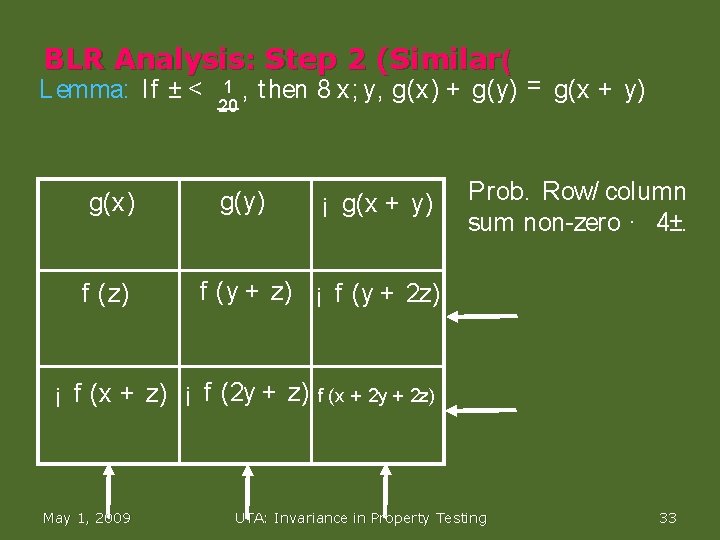
BLR Analysis: Step 2 (Similar( Lemma: If ± < g(x) f (z) 1 , 20 t hen 8 x; y, g(x) + g(y) = g(x + y) g(y) ¡ g(x + y) Prob. Row/ column sum non zero · 4±. f (y + z) ¡ f (y + 2 z) ¡ f (x + z) ¡ f (2 y + z) f (x + 2 y + 2 z) May 1, 2009 UTA: Invariance in Property Testing 33

Our Analysis: Outline ² f s. t. Pr L [hf (L (x 1 ); : : : ; f (L (x k ))i 2 V ] = ± ¿ 1. ² De¯ne g(x) = ® t hat maximizes Pr f L j L ( x ) = x g [h®; f (L (x 2 )); : : : ; f (L (x k ))i 2 V ] 1 ² St eps: ¡ St ep 0: Prove f close t o g ¡ Step 1: Prove “most likely” is overwhelming majority. ¡ St ep 2: Prove t hat g is in F. May 1, 2009 UTA: Invariance in Property Testing 34

Our Analysis: Outline ² f s. t. Pr L [hf (L (x 1 ); : : : ; f (L (x k ))i 2 V ] = ± ¿ 1. ² De¯ne g(x) = ® t hat maximizes Pr f L j L ( x ) = x g [h®; f (L (x 2 )); : : : ; f (L (x k ))i 2 V ] 1 Same as before ² St eps: ¡ St ep 0: Prove f close t o g ¡ Step 1: Prove “most likely” is overwhelming majority. ¡ St ep 2: Prove t hat g is in F. May 1, 2009 UTA: Invariance in Property Testing 35

Vot ex (L ) Matrix ? ² De¯ne Magic g(x) = ® t hat maximizes Pr f L j L ( x = 1) xg [h®; f (L (x 2 )); : : : ; f (L (x k ))i 2 V ] 6 Vot ex (K ))] · 2(k ¡ 1)± Lemma: 8 x, Pr L ; K [Vot ex (L ) = x K (x 2 ). . . L (x 2 ) ? ¢¢¢ L (x k ) K (x k ) May 1, 2009 UTA: Invariance in Property Testing 36

Matrix Magic? x K (x 2 ). . . L (x 2 ) ? ¢¢¢ L (x k ) K (x k ) ² Want marked rows t o be random const raint s. ² Suppose x 1 ; : : : ; x ` linearly independent ; and rest dependent on t hem.

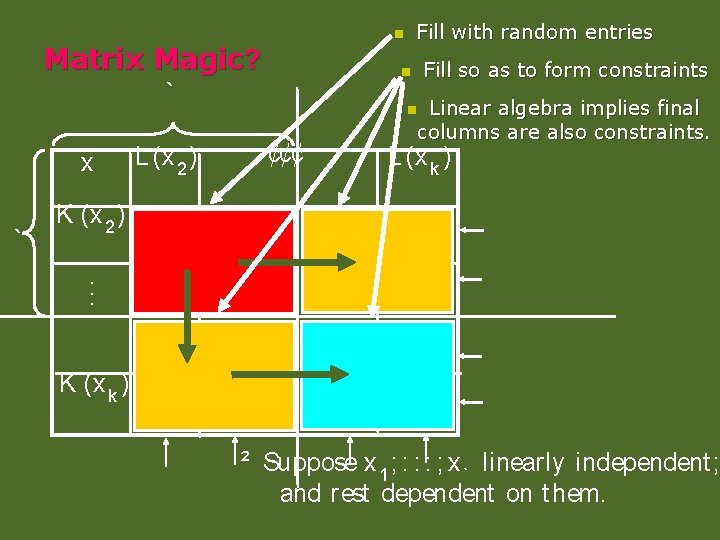
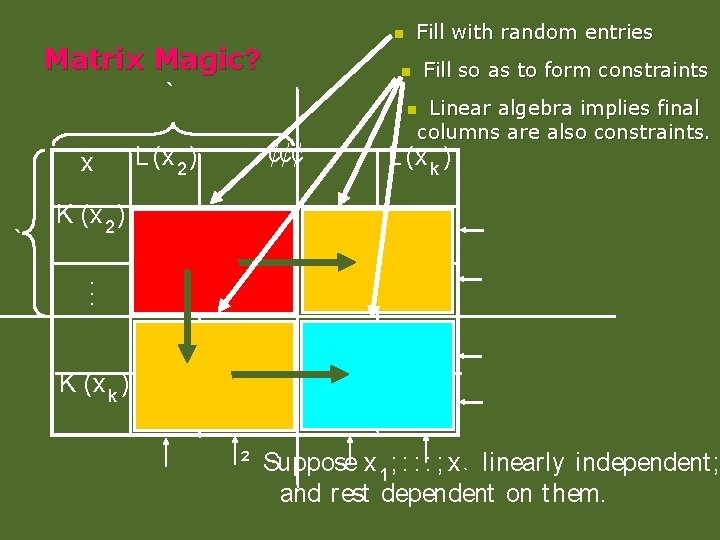
Matrix Magic? n ` x ` L (x 2 ) Fill with random entries n n ¢¢¢ Fill so as to form constraints Linear algebra implies final columns are also constraints. L (x k ) K (x 2 ). . . K (x k ) ² Suppose x 1 ; : : : ; x ` linearly independent ; and rest dependent on t hem.

Matrix Magic? n ` x ` L (x 2 ) Fill with random entries n n ¢¢¢ Fill so as to form constraints Linear algebra implies final columns are also constraints. L (x k ) K (x 2 ). . . K (x k ) ² Suppose x 1 ; : : : ; x ` linearly independent ; and rest dependent on t hem.

Conclusions n n n Invariance is important in property testing. Linear-invariance suffices to explain many algebraic tests (and shows some new ones. ( Future work: What are other invariances that lead to testability (from characterizations? ( May 1, 2009 UTA: Invariance in Property Testing 40