Introduzione alle equazioni di Maxwell Equazioni di Maxwell























- Slides: 55

Introduzione alle equazioni di Maxwell

Equazioni di Maxwell /1 S • Forza di Lorentz: definizione operativa di E e B • Unità di misura • Flusso (magnetico) concatenato con

Equazioni di Maxwell /2 • Definizione di , J e unità di misura • H, D: relazioni costitutive nel vuoto • Corrente di conduzione e corrente di spostamento • Onde elettromagnetiche • Cenni storici

Forma differenziale • Teorema di Stokes e della divergenza • Non equivalenza tra forma integrale e differenziale • Conservazione della carica (forma integrale)

Modelli statici • Relazioni costitutive nei materiali più comuni • Disaccoppiamento in “sottomodelli” autoconsistenti a seconda dei materiali • Elettrostatica (ES), conduzione stazionaria (CS), magnetostatica (MS) • Forma integrale

Modelli quasi statici • Una derivata trascurabile, l’altra no • Variazioni temporali, ma “lente” • Elettroquasistatica (EQS), magnetoquasistatica (MQS) • Forma integrale

Conduzione stazionaria

Equazioni • E conservativo, J solenoidale • Resistività , conducibilità

Materiali e geometrie • Conduttori perfetti e isolanti perfetti – “Approssimazioni” di isolanti perfetti – Superconduttori • Tubo di flusso

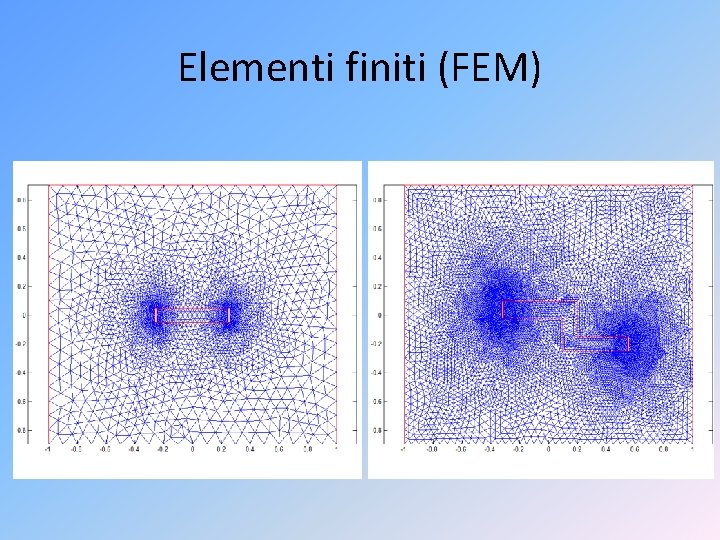
Elementi finiti (FEM)

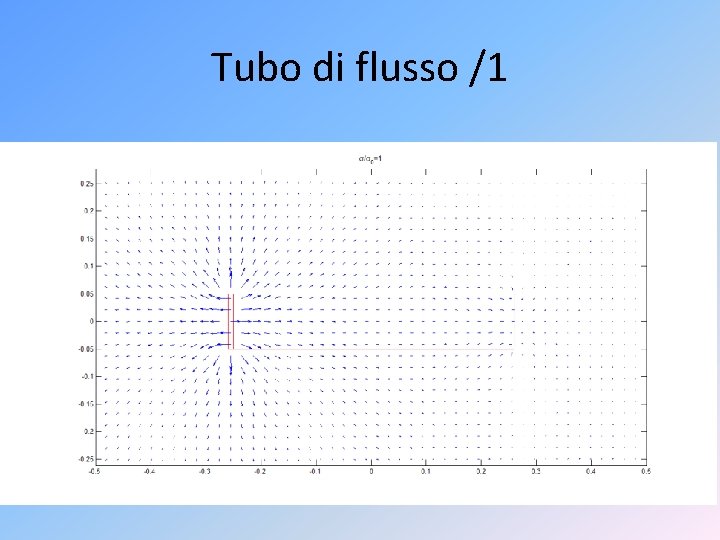
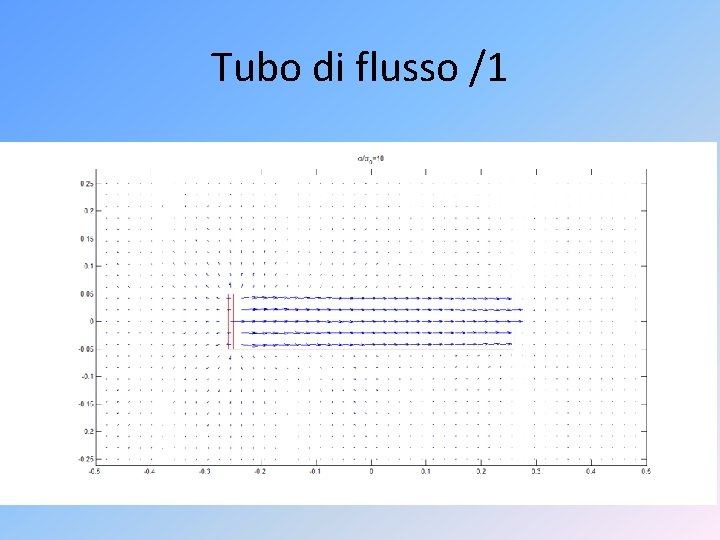
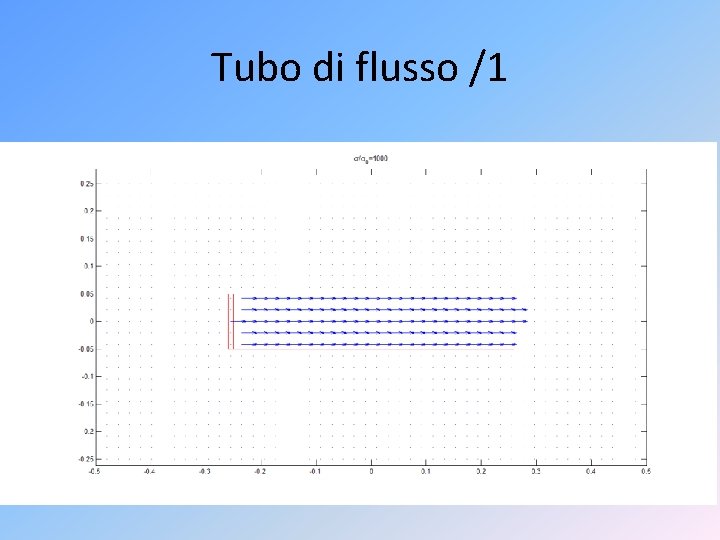
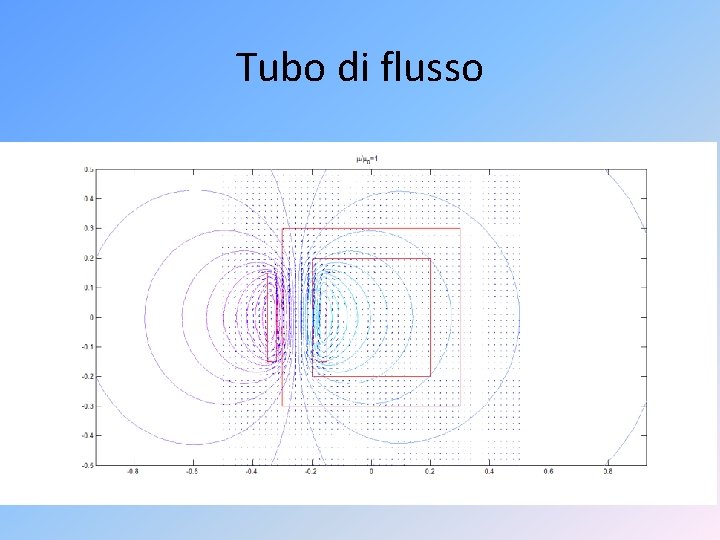
Tubo di flusso /1

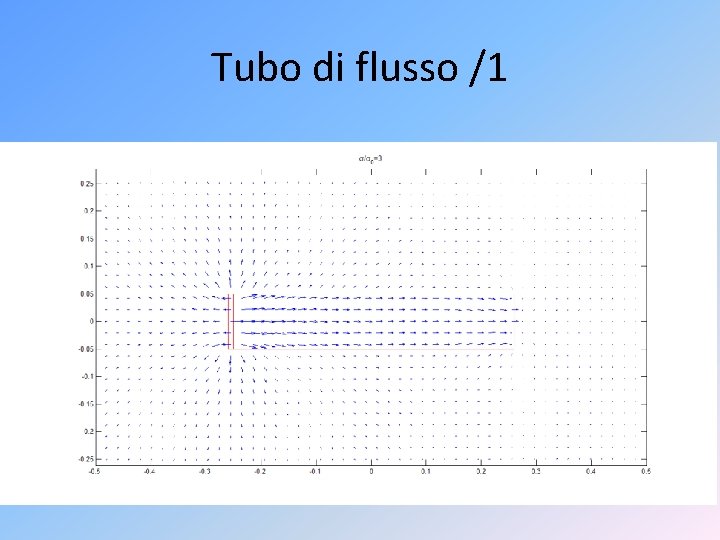
Tubo di flusso /1

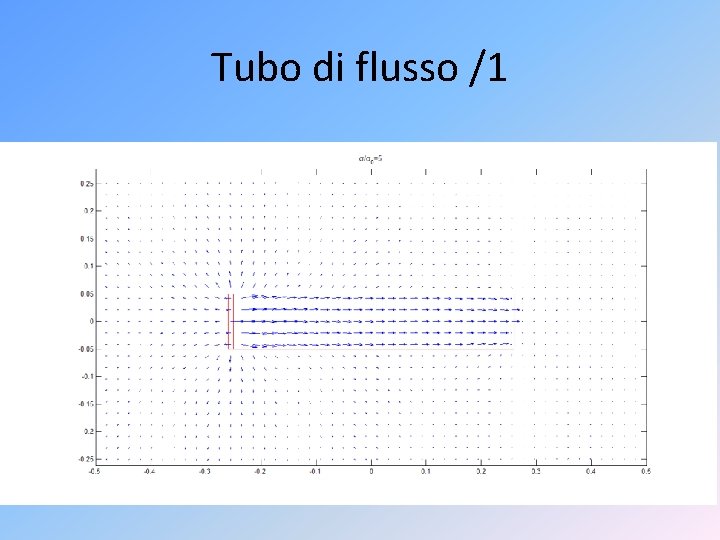
Tubo di flusso /1

Tubo di flusso /1

Tubo di flusso /1

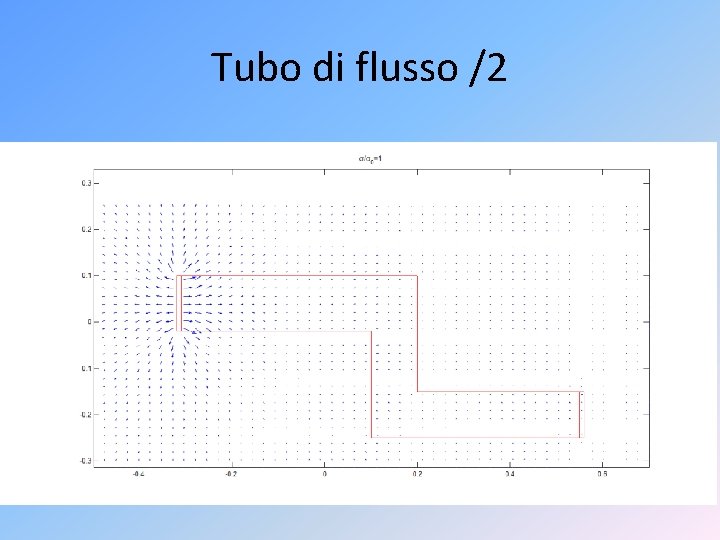
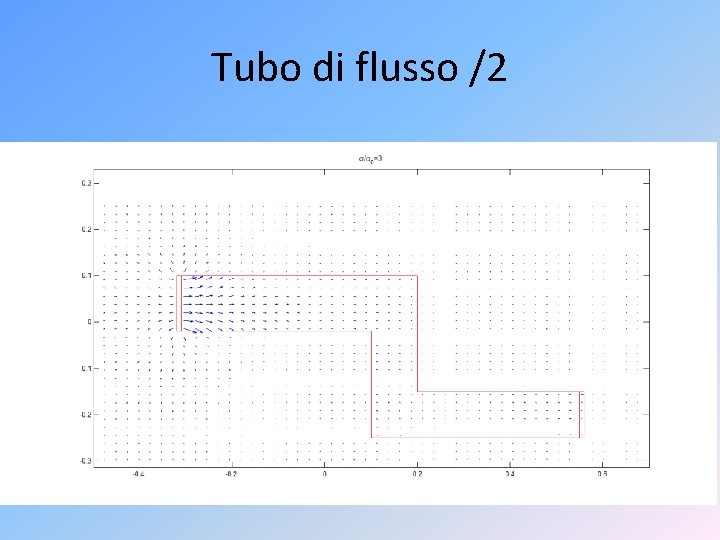
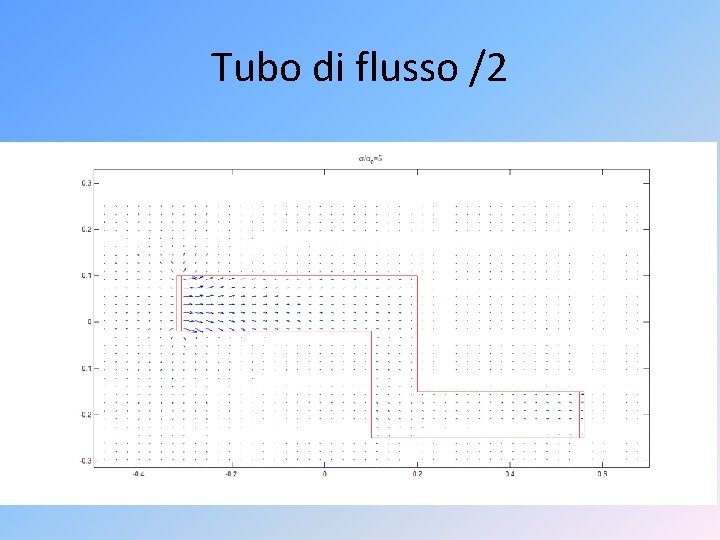
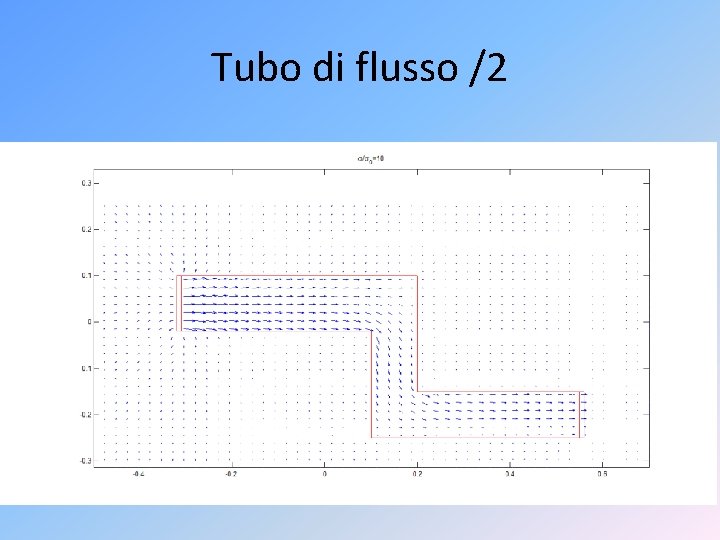
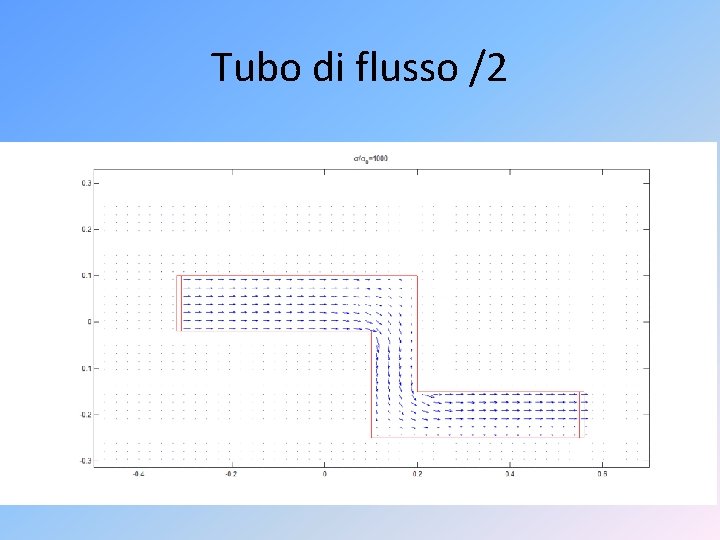
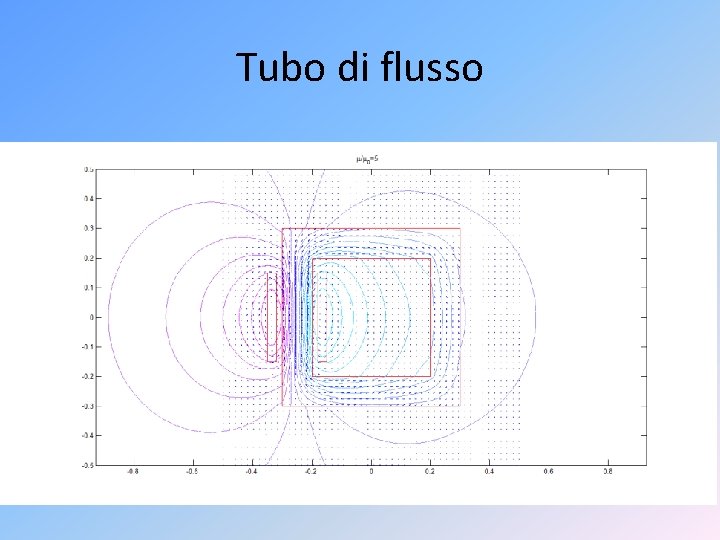
Tubo di flusso /2

Tubo di flusso /2

Tubo di flusso /2

Tubo di flusso /2

Tubo di flusso /2

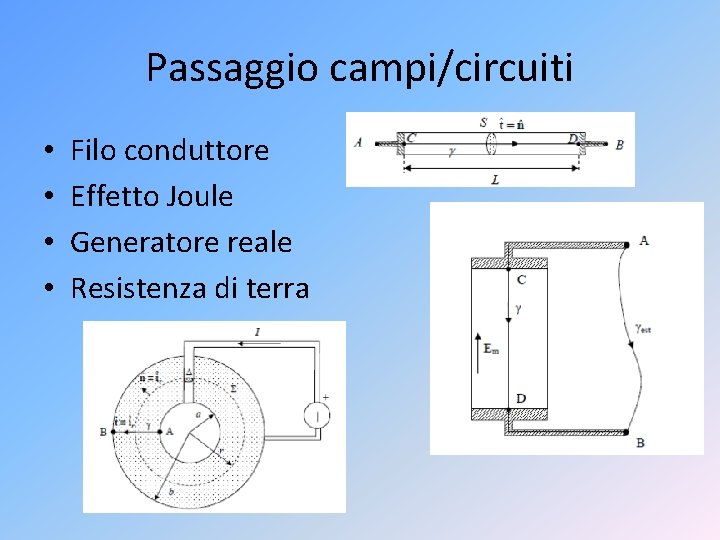
Passaggio campi/circuiti • • Filo conduttore Effetto Joule Generatore reale Resistenza di terra

Elettro(quasi)statica

Equazioni • E conservativo • Potenziale scalare, equazione di Poisson

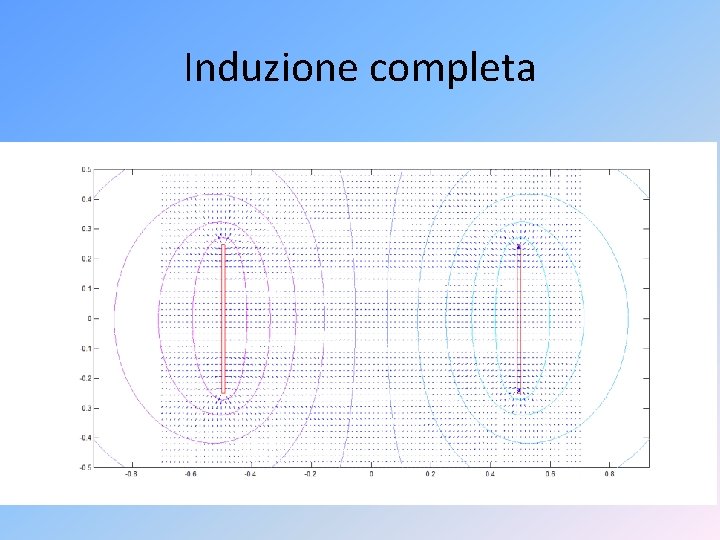
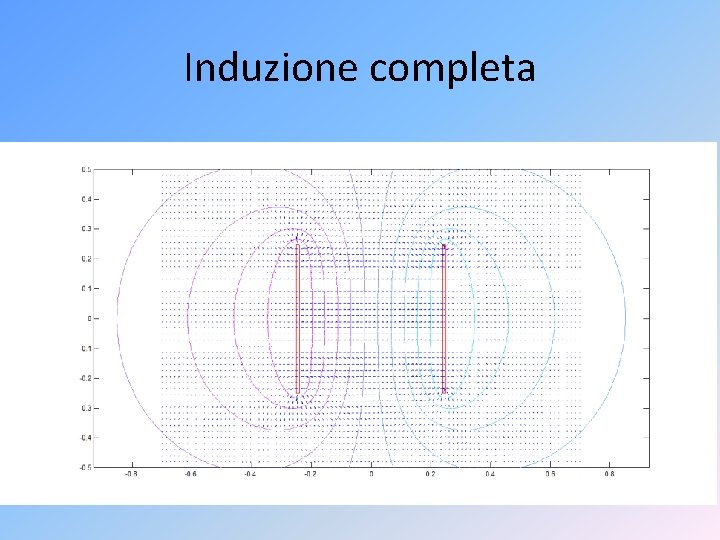
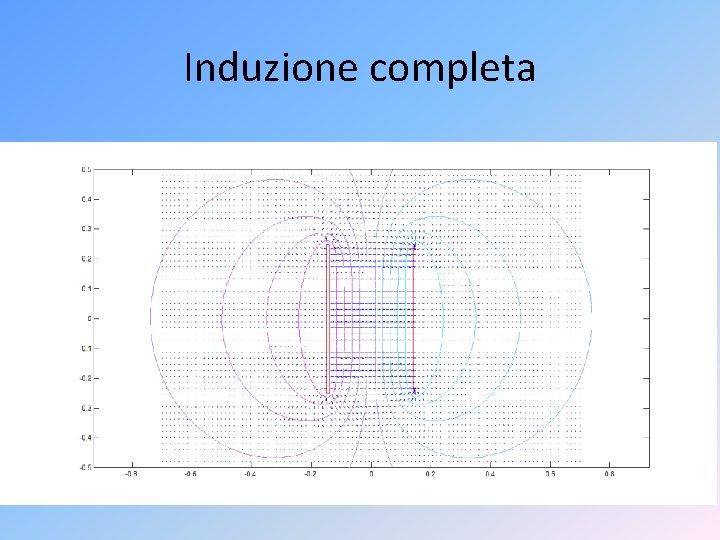
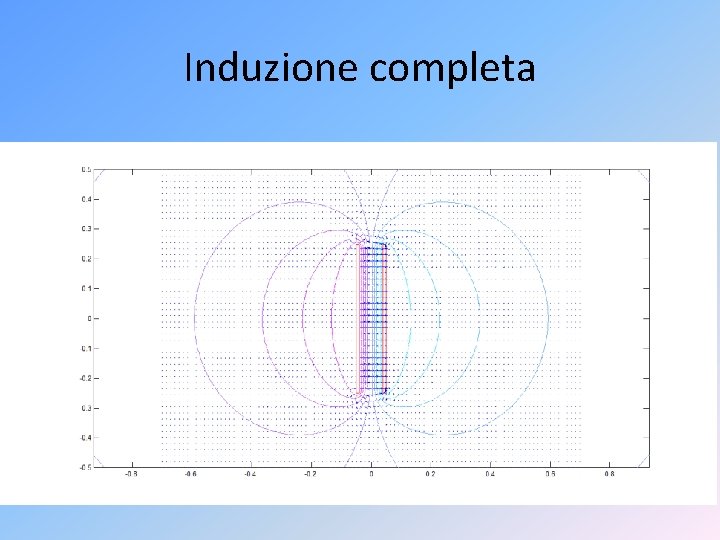
Materiali e geometrie • Materiali conduttori o Un elettrodo: potere delle punte (link) o Due elettrodi: linee di campo ed equipotenziali • Materiali dielettrici: assenza di tubo di flusso • Induzione completa • Passaggio campi-circuiti

Induzione completa

Induzione completa

Induzione completa

Induzione completa

Magneto(quasi)statica nel vuoto

Equazioni • B solenoidale, potenziale vettore

Configurazioni elementari • • • Filo rettilineo indefinito Spira Solenoide rettilineo indefinito Solenoide toroidale Autoinduttanza Passaggio campi-circuiti

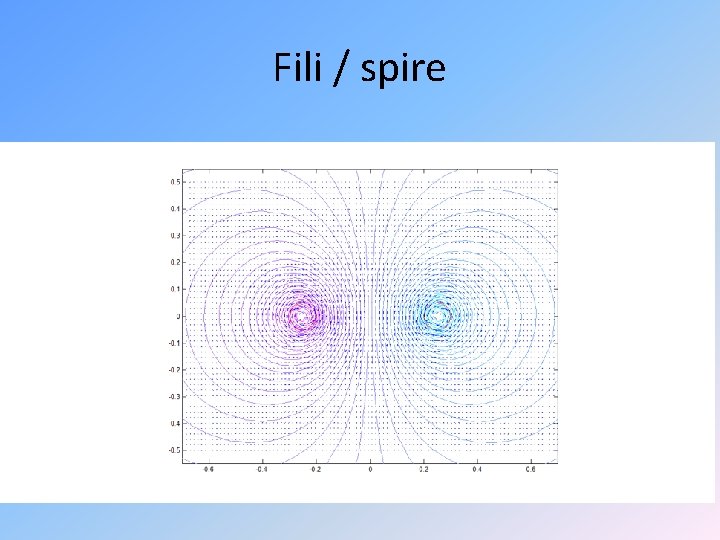
Fili / spire

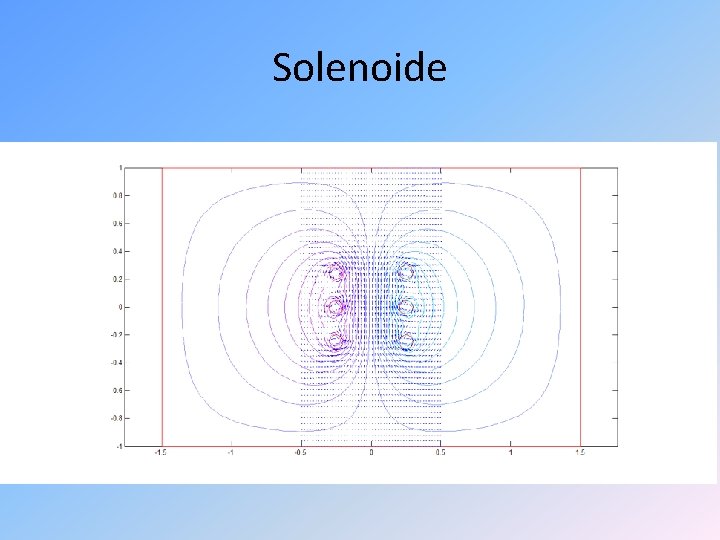
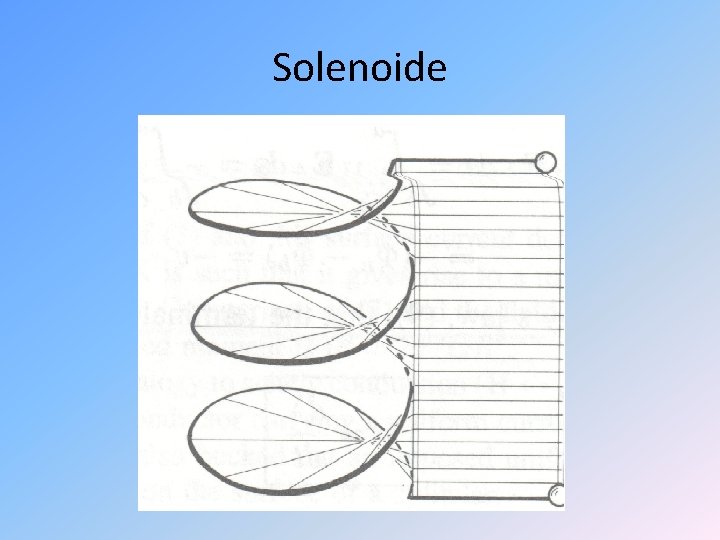
Solenoide

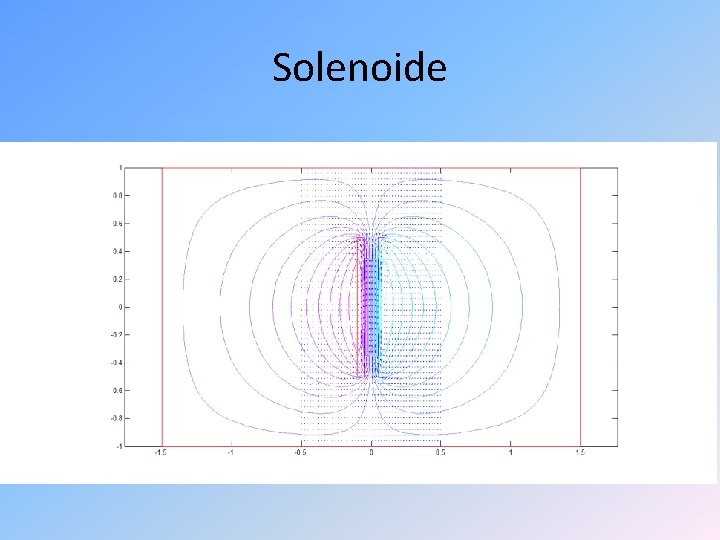
Solenoide

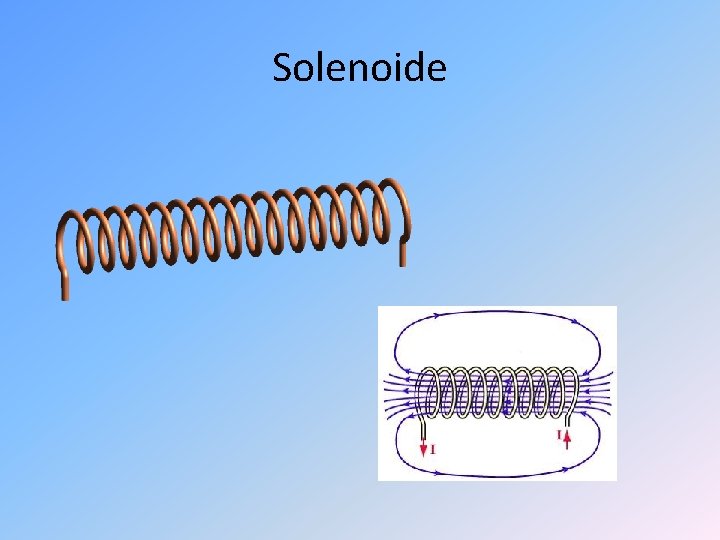
Solenoide

Solenoide

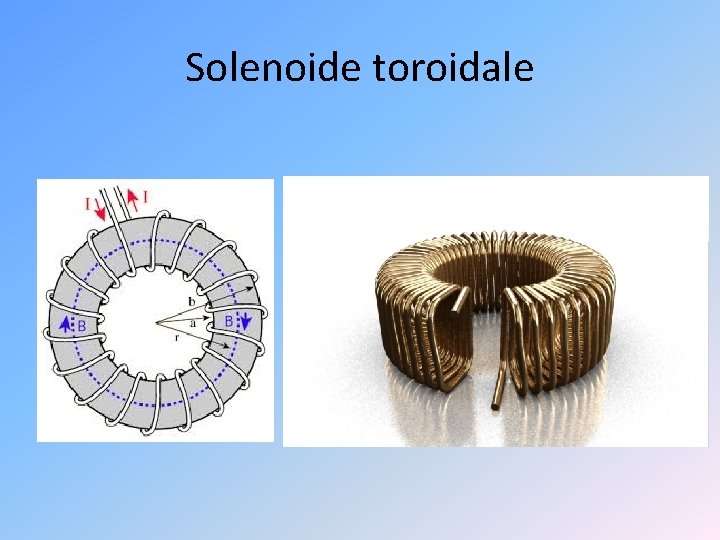
Solenoide toroidale

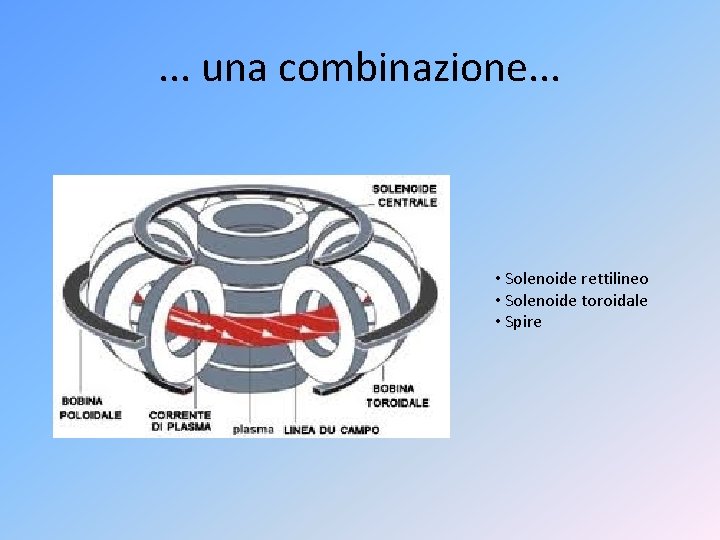
. . . una combinazione. . . • Solenoide rettilineo • Solenoide toroidale • Spire

Circuiti mutuamente accoppiati • Mutua induttanza • Passaggio campi-circuiti • Tensione e corrente indotta

Le leggi di Kirchhoff e la potenza

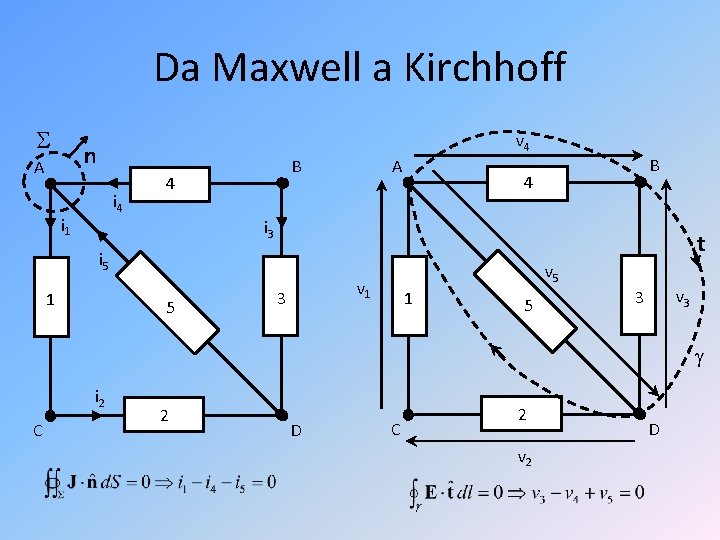
Da Maxwell a Kirchhoff • Nei «bipoli fisici» visti precedentemente, nella regione esterna al bipolo: – Derivata dell’induzione magnetica trascurabile tensione indotta trascurabile su linee «esterne» – Derivata dello spostamento elettrico trascurabile corrente di spostamento trascurabile su superfici «esterne» • In queste stesse ipotesi, valgono le leggi di Kirchhoff sulle «connessioni fisiche» – J solenoidale: corrente di conduzione uscente da una superficie chiusa pari a zero – E conservativo: tensione su una linea chiusa pari a zero

Da Maxwell a Kirchhoff v 4 n A i 4 i 1 A B 4 i 3 t i 5 1 5 v 1 3 1 5 v 3 3 i 2 C 2 D C 2 v 2 D

Teorema di Poynting • Combinando le equazioni di Maxwell nel vuoto • Vettore di Poynting: S = E x H

Teorema di Poynting • Integrando su un volume fisso nel tempo: • Wel, Wmag: energia elettrica e magnetica all’interno di • PJ: potenza dissipata per effetto Joule all’interno di • PEM: potenza sviluppata dal campo elettromotore sulle cariche in moto

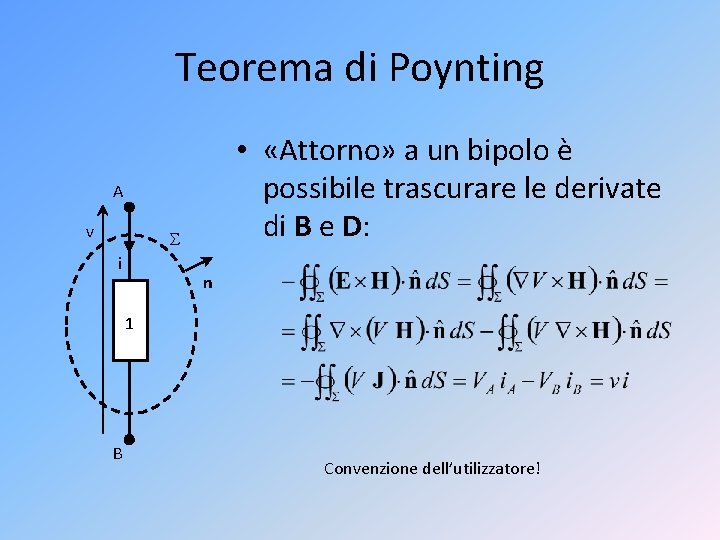
Teorema di Poynting • «Attorno» a un bipolo è possibile trascurare le derivate di B e D: A v i n 1 B Convenzione dell’utilizzatore!

Teorema di Poynting • In definitiva: • Aggiungendo opportune considerazioni termodinamiche (primo principio), possiamo interpretare il prodotto v i con la convenzione dell’utilizzatore (potenza assorbita della teoria dei circuiti) come la «potenza elettromagnetica» entrante nel sistema tramite i morsetti: – Resistore: vi = potenza dissipata per effetto Joule – Generatore ideale: vi = - potenza sviluppata dal campo elettromotore – Condensatore: vi = derivata dell’energia del campo elettrico tra le armature – Induttore: vi = derivata dell’energia del campo magnetico tra le spire

Magnetostatica nei mezzi materiali

Mezzi magnetici • Paramagnetici, diamagnetici: poco interessanti • Ferromagnetici – Ciclo di isteresi – Perdite – Semplificazioni per materiali dolci non saturi • Tubo di flusso, traferri • Circuiti magnetici, leggi di Hopkinson

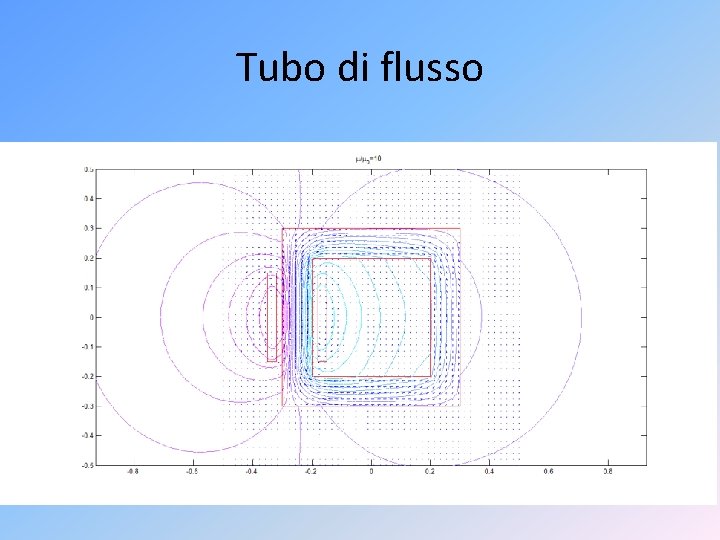
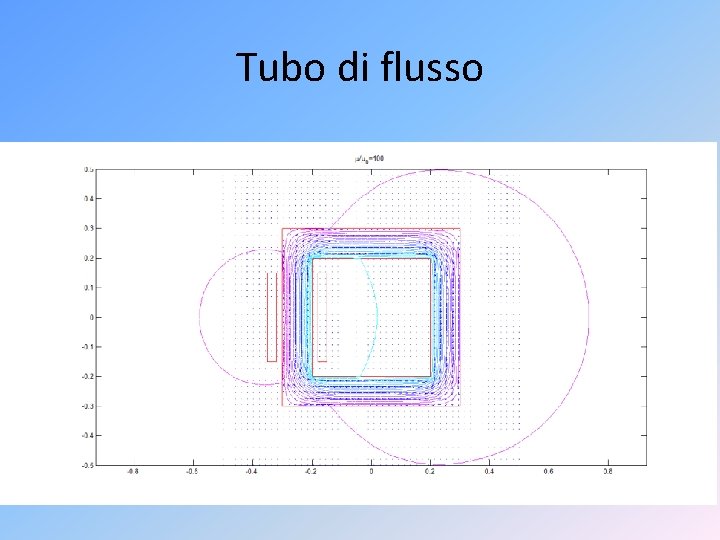
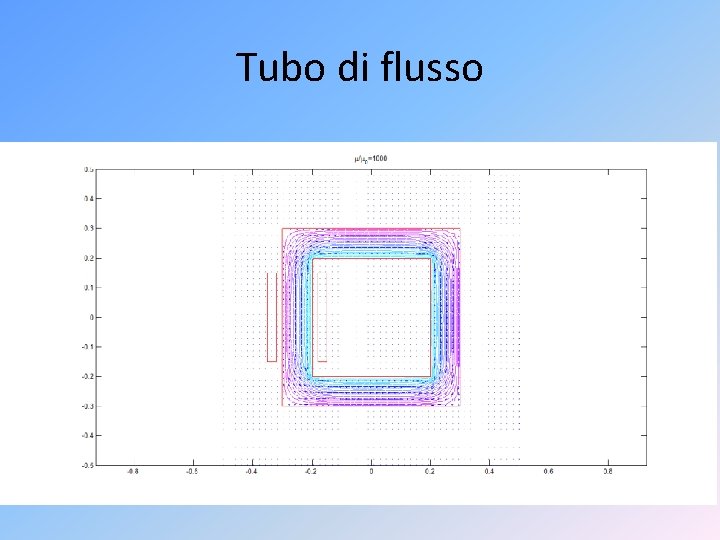
Tubo di flusso

Tubo di flusso

Tubo di flusso

Tubo di flusso

Tubo di flusso

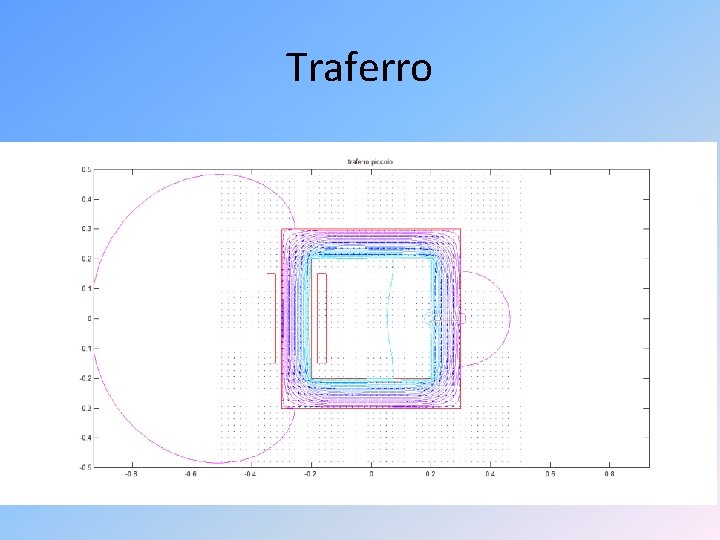
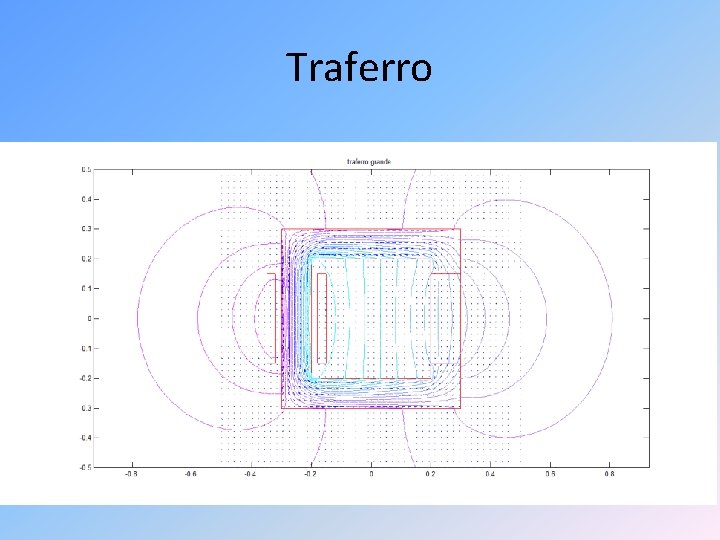
Traferro

Traferro