Introduzione allalgebra lineare Marco Casarotti Universit di Padova

Introduzione all’algebra lineare Marco Casarotti (Università di Padova) Paolo Bouquet (Università di Trento)

Algebra lineare Definizione di Matrice: Tabella di numeri – detti coefficienti – disposti in righe e colonne: indici

Esempi: n m

Matrici quadrate: Il numero di righe è uguale al numero di colonne: A m x m m è chiamato ordine della matrice Esempio di matrice avente ordine 4

Definizioni Diagonale principale: Insieme dei coefficienti con indice (i, i) con 1≤i≤m

Definizioni Diagonale secondaria: Insieme dei coefficienti con indice (i, m-i+1) con 1≤i≤m

Definizioni Matrici diagonali: Sono matrici quadrate i cui coefficienti NON diagonali sono uguali a 0. Esempi:

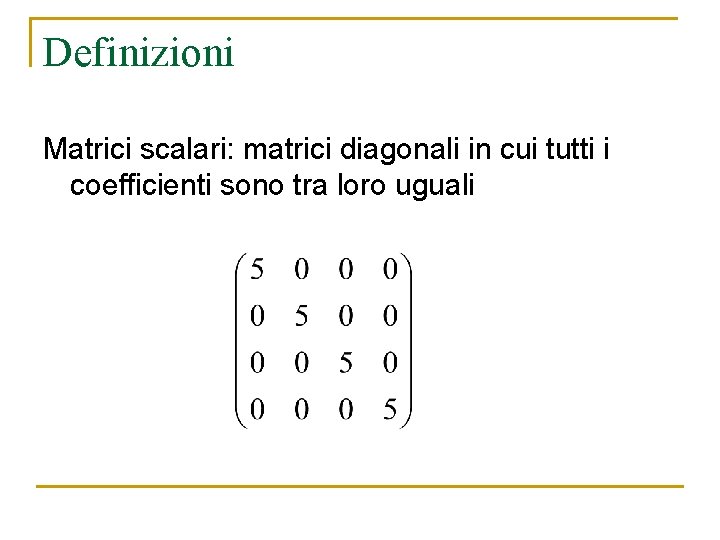
Definizioni Matrici scalari: matrici diagonali in cui tutti i coefficienti sono tra loro uguali

Vettori Matrice 1 xn: vettore riga ( ) Matrice mx 1: vettore colonna ( u )

Prodotto scalare: data una matrice A ed uno scalare α, si definisce prodotto scalare la matrice αA tale che:

Definizioni Si definisce –A, la matrice OPPOSTA di A: Proprietà del prodotto scalare: • 1 A=A • 0 A=0 • (xy)A=x(y. A)

Somma di matrici (per componenti) Date due matrici A e B delle medesime dimensioni, si definisce come loro somma la matrice A+B tale che: La somma di matrici aventi diverse dimensioni NON è definita.

Prodotto per componenti Date due matrici A e B delle medesime dimensioni, si definisce come loro prodotto per componenti la matrice C tale che:

Prodotto di un vettore riga per un vettore colonna Dati un vettore riga ed un vettore colonna u con lo stesso numero di elementi, ovvero rispettivamente 1 xn e nx 1, si definisce prodotto riga per colonna il valore (o matrice 1 x 1):

Esempio di prodotto riga

Prodotto di matrici righe per colonne Siano A e B due matrici tali che il numero di colonne di A sia uguale al numero di righe di B. Definiamo il prodotto di A e B righe per colonne come la matrice C ottenuta eseguendo il prodotto di vettore riga per vettore colonna tra tutte le righe di A e tutte le colonne di B. La matrice C avrà lo stesso numero di righe di A e lo stesso numero di colonne di B.

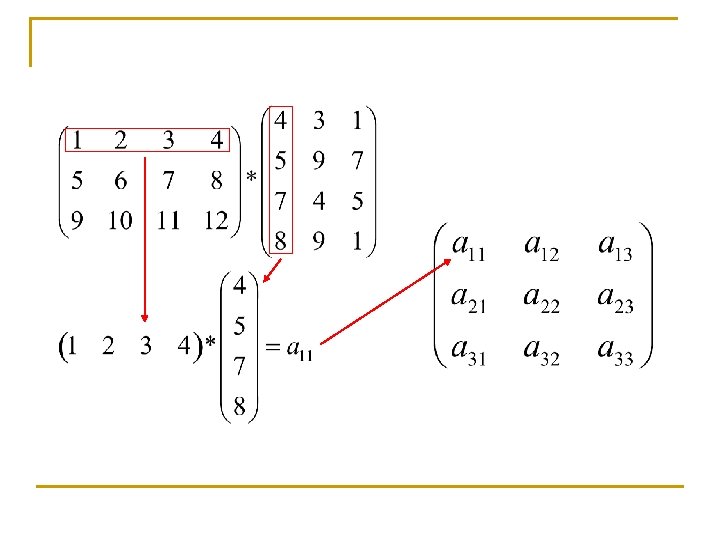
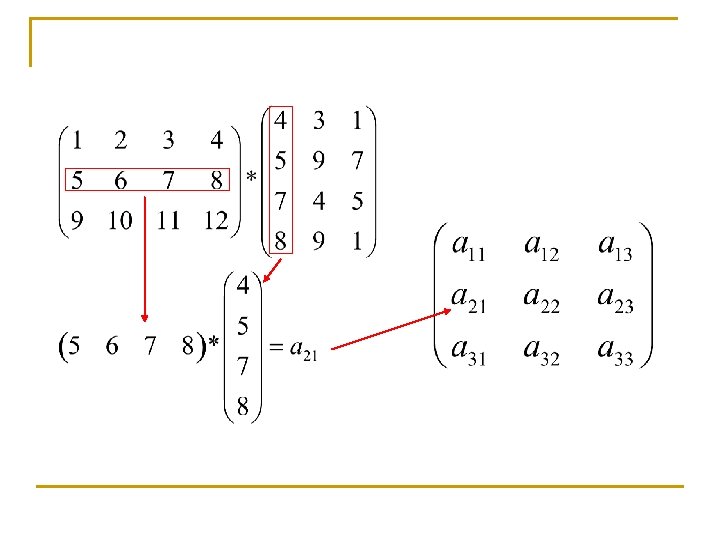
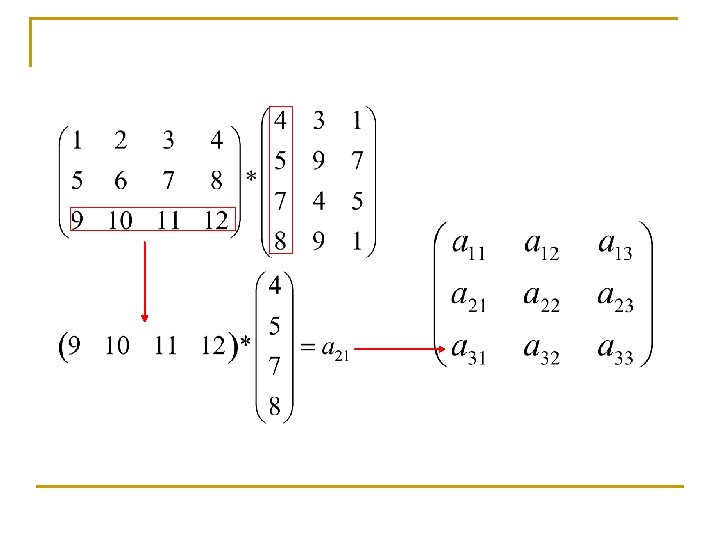
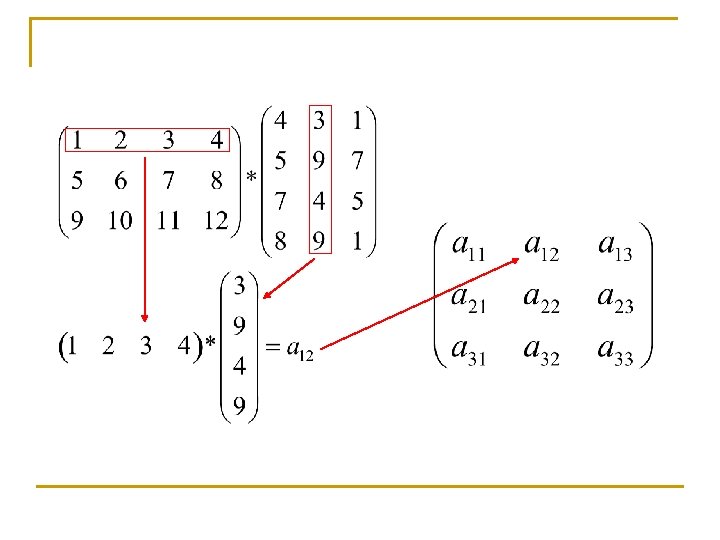
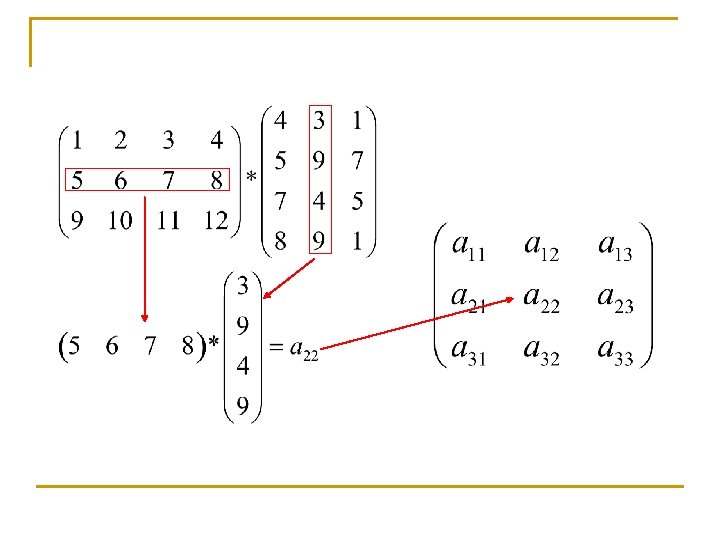
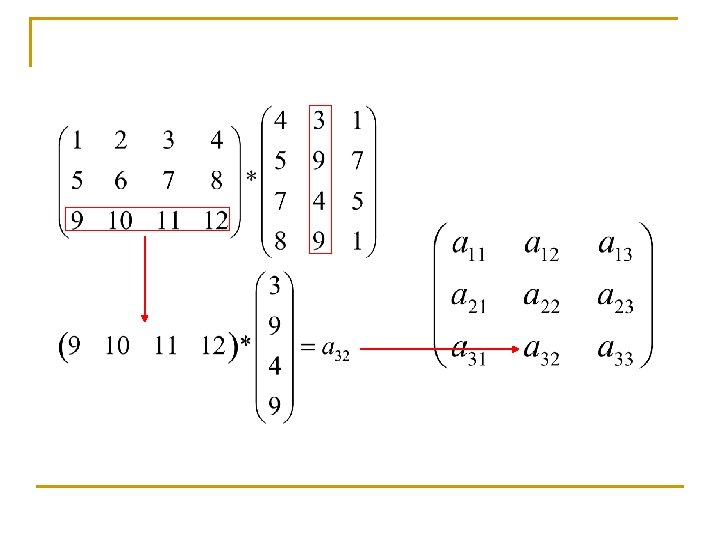
Prodotto di un vettore colonna per un vettore riga Il prodotto di un vettore colonna u per un vettore riga è una matrice C ottenuta calcolando il prodotto per componenti di una matrice A avente tante colonne, tutte uguali ad u, quante sono le righe di una matrice B avente tante righe, tutte uguali ad quante sono le righe di u.

Esempio di prodotto di vettore colonna per vettore riga . * =

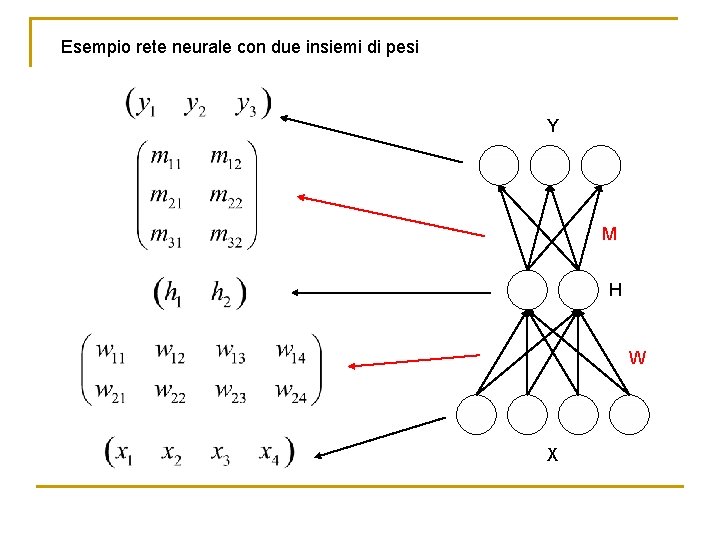
Esempio rete neurale con due insiemi di pesi Y M H W X