Introduo to Geoinformatics Topology The benefits of axiomatization

Introdução to Geoinformatics: Topology

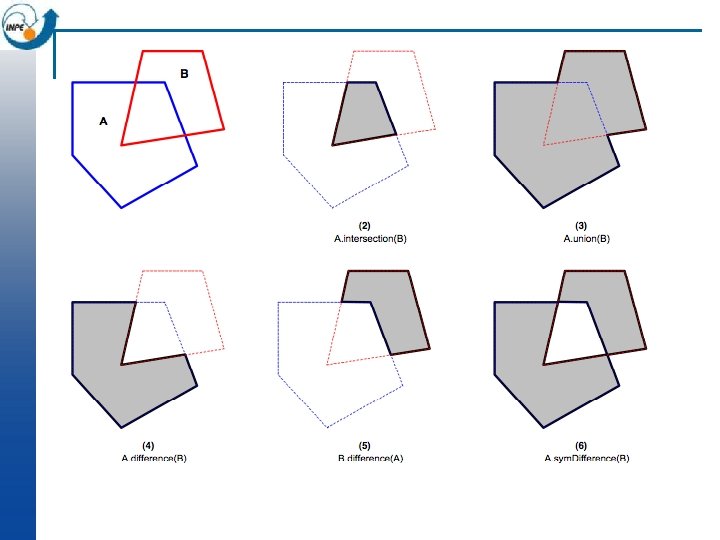
The benefits of axiomatization Euclid (x + y)2 = x 2 + 2 xy + y 2

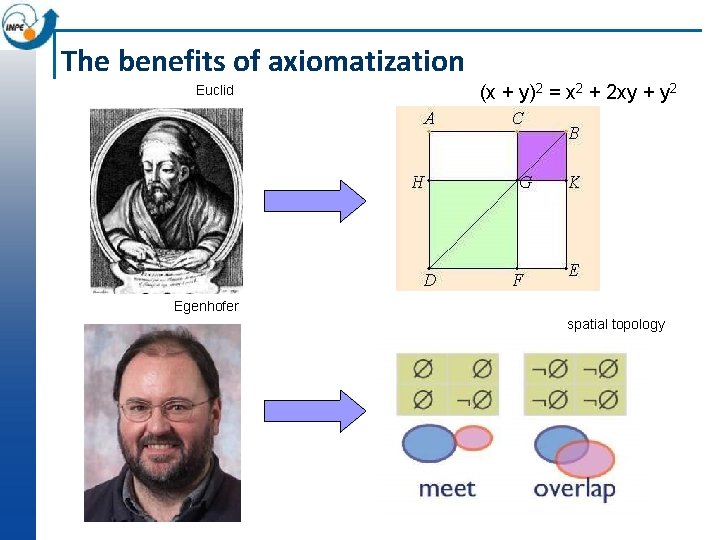
The benefits of axiomatization Euclid (x + y)2 = x 2 + 2 xy + y 2 Egenhofer spatial topology

The Axiomatization of science Newton

The Axiomatization of informatics Codd

The Axiomatization of geoinformatics Güting Frank

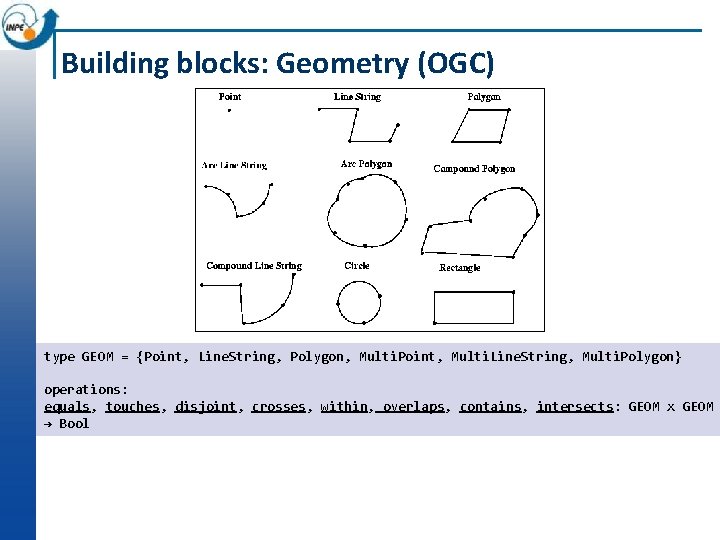
Building blocks: Geometry (OGC) type GEOM = {Point, Line. String, Polygon, Multi. Point, Multi. Line. String, Multi. Polygon} operations: equals, touches, disjoint, crosses, within, overlaps, contains, intersects: GEOM x GEOM → Bool

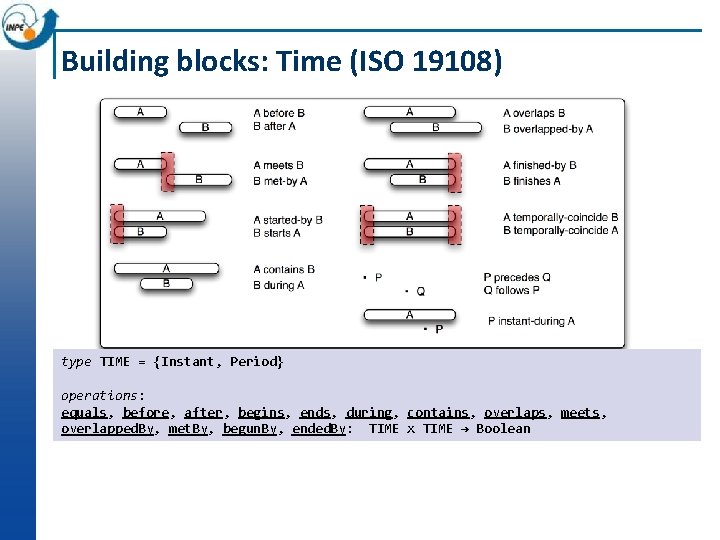
Building blocks: Time (ISO 19108) type TIME = {Instant, Period} operations: equals, before, after, begins, ends, during, contains, overlaps, meets, overlapped. By, met. By, begun. By, ended. By: TIME x TIME → Boolean

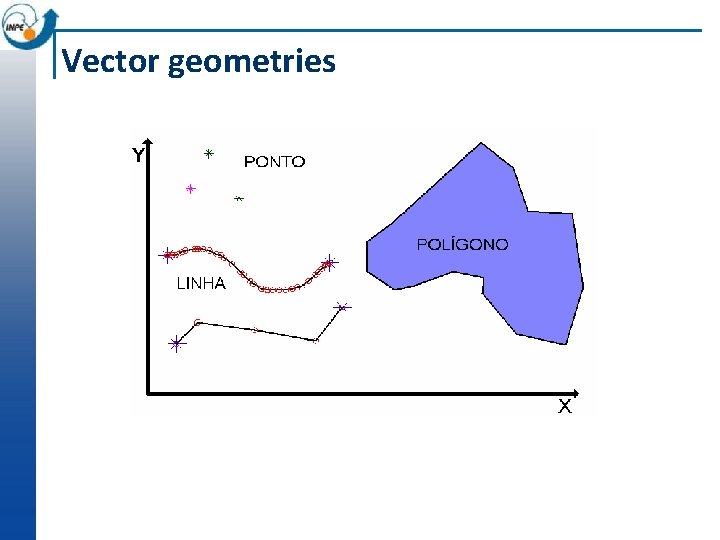
Vector geometries

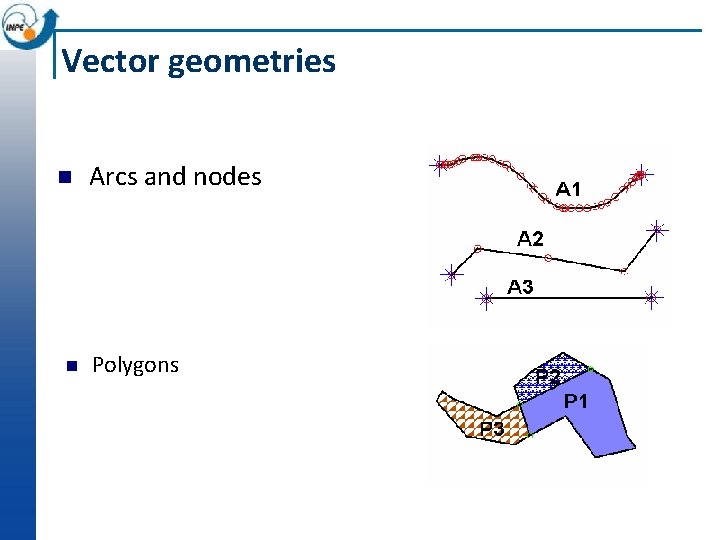
Vector geometries n n Arcs and nodes Polygons

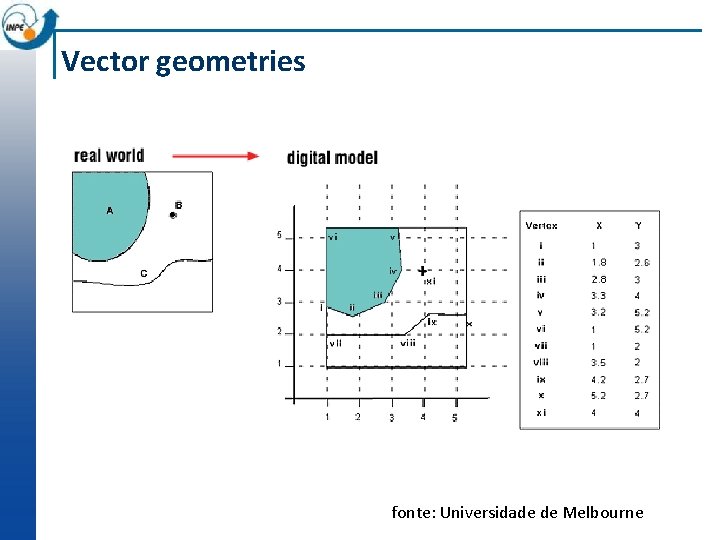
Vector geometries fonte: Universidade de Melbourne

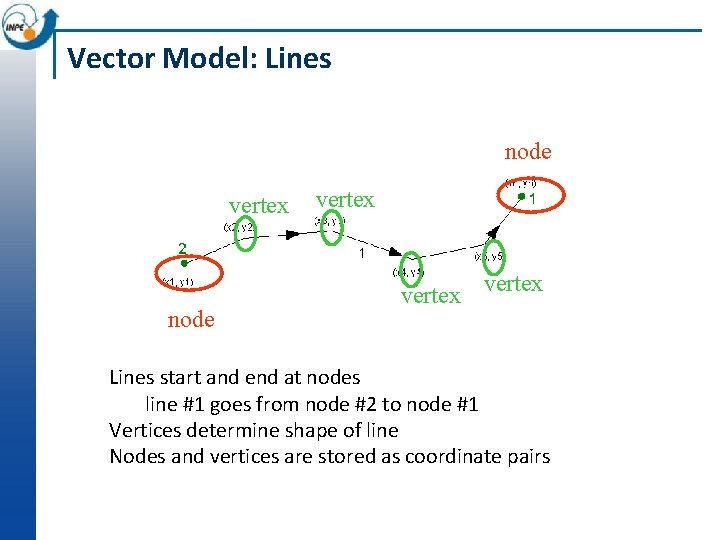
Vector Model: Lines node vertex Lines start and end at nodes line #1 goes from node #2 to node #1 Vertices determine shape of line Nodes and vertices are stored as coordinate pairs

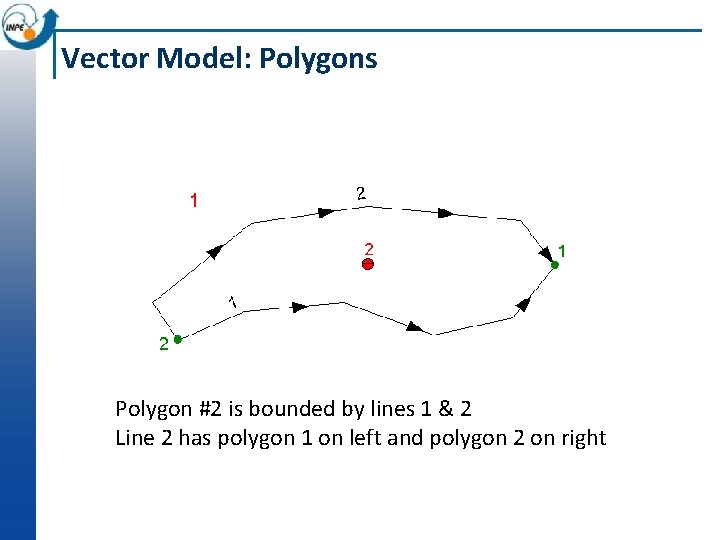
Vector Model: Polygons Polygon #2 is bounded by lines 1 & 2 Line 2 has polygon 1 on left and polygon 2 on right

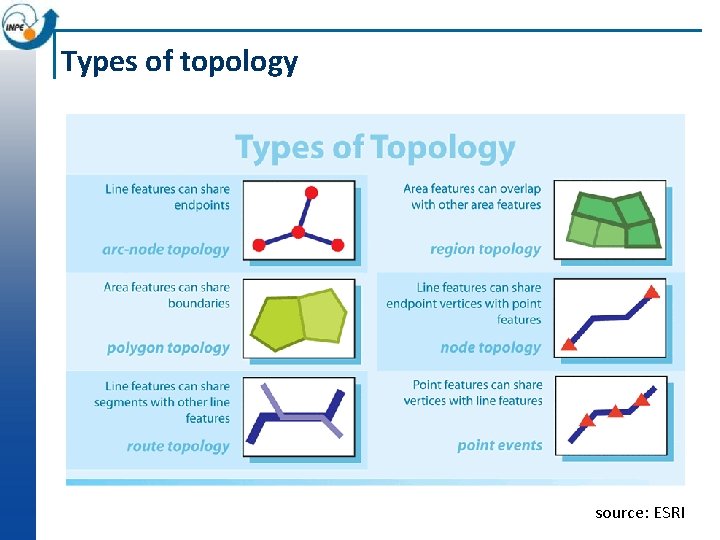
Types of topology source: ESRI

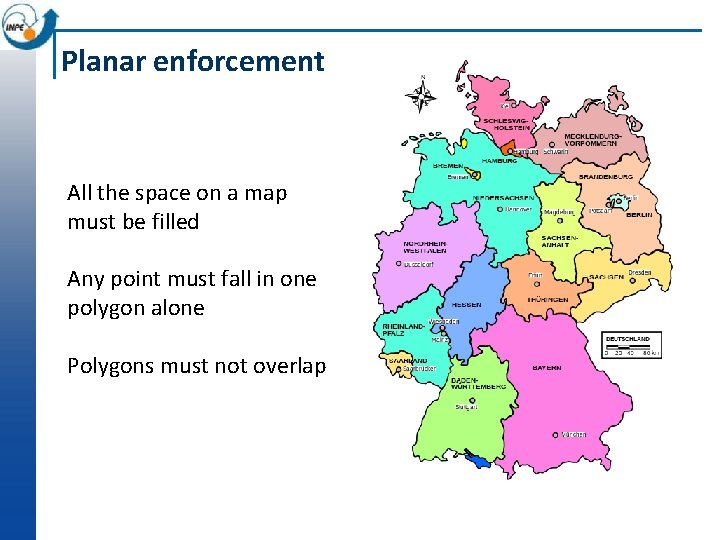
Planar enforcement All the space on a map must be filled Any point must fall in one polygon alone Polygons must not overlap

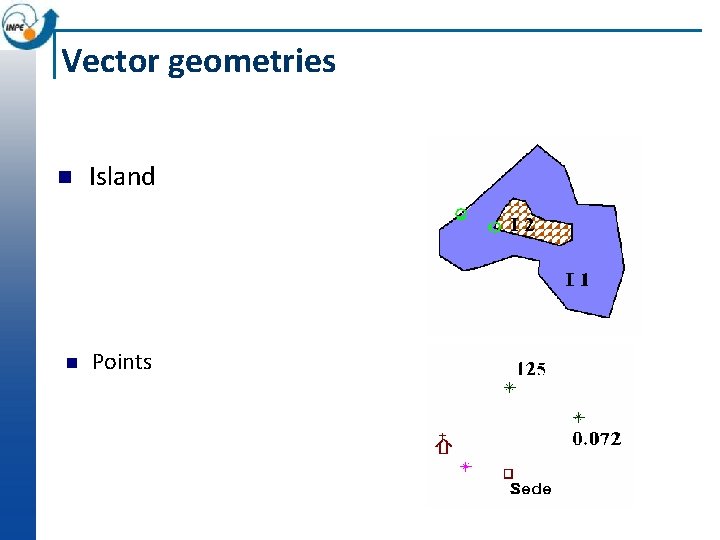
Vector geometries n Island n Points

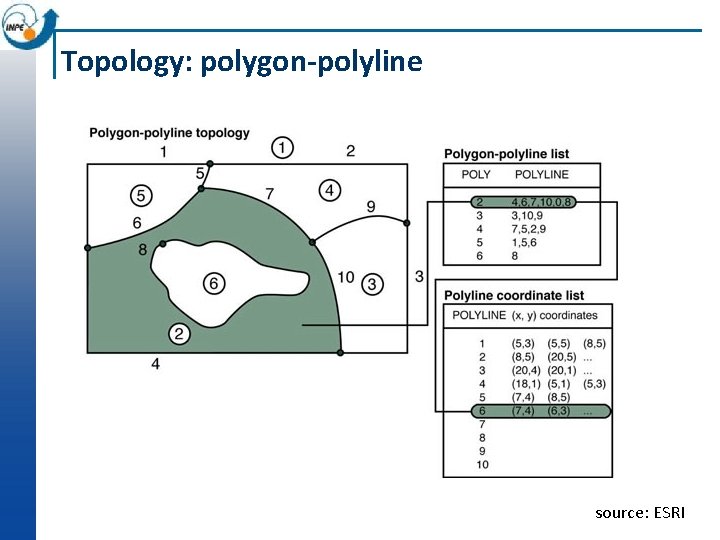
Topology: polygon-polyline source: ESRI

Topology: polygon-polyline Shapefile polygon spatial data model • less complex data model • polygons do not share bounding lines

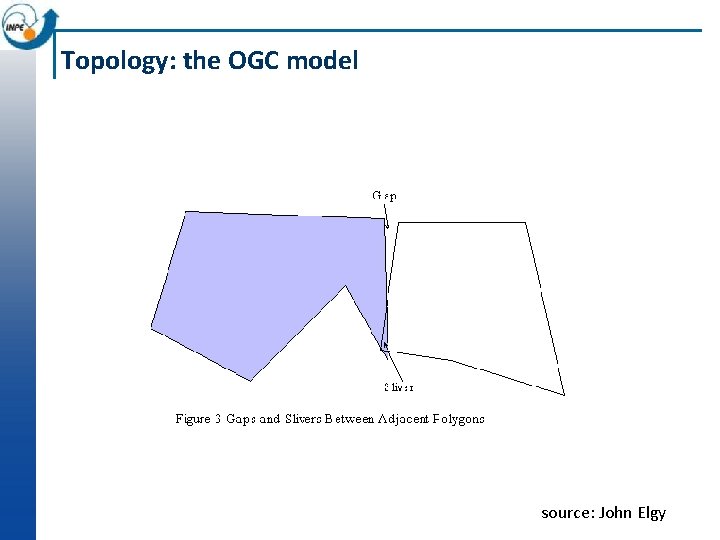
Topology: the OGC model source: John Elgy

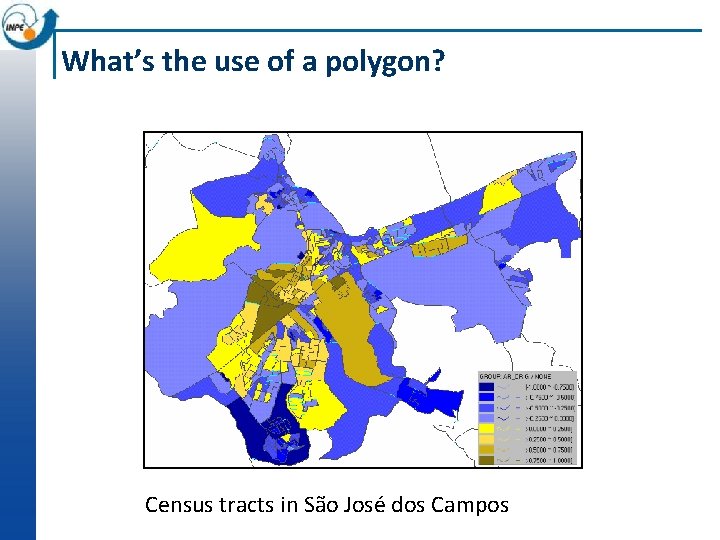
What’s the use of a polygon? Census tracts in São José dos Campos

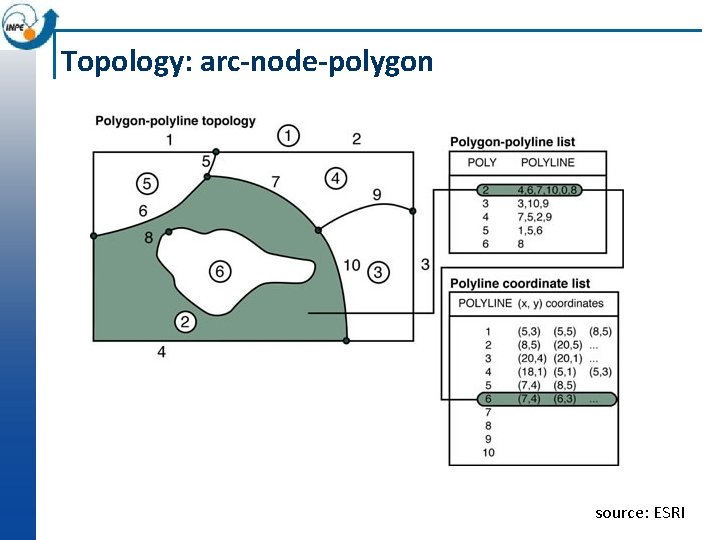
Topology: arc-node-polygon source: ESRI

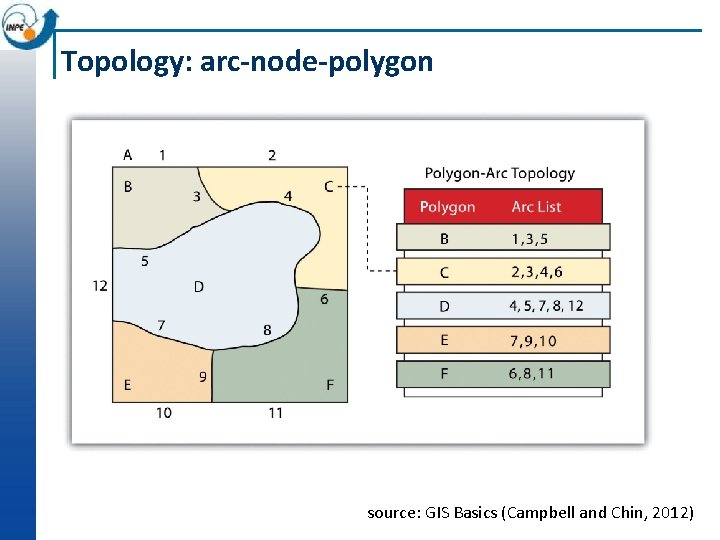
Topology: arc-node-polygon source: GIS Basics (Campbell and Chin, 2012)

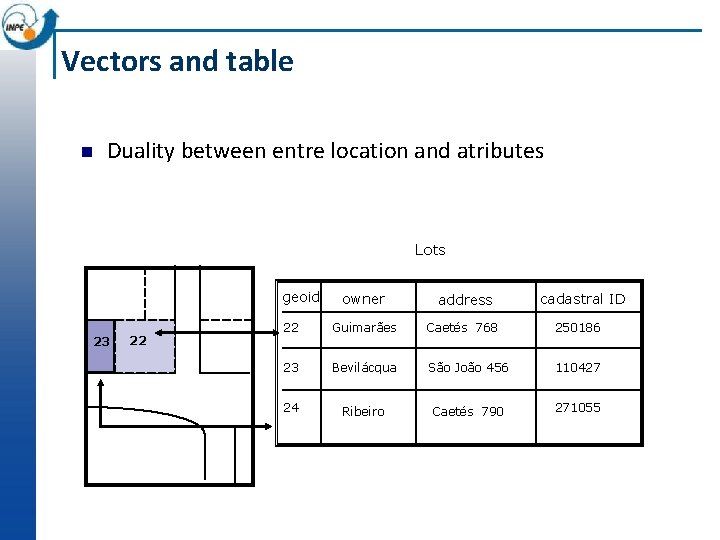
Vectors and table n Duality between entre location and atributes Lots geoid 23 22 owner address cadastral ID 22 Guimarães Caetés 768 250186 23 Bevilácqua São João 456 110427 24 Ribeiro Caetés 790 271055

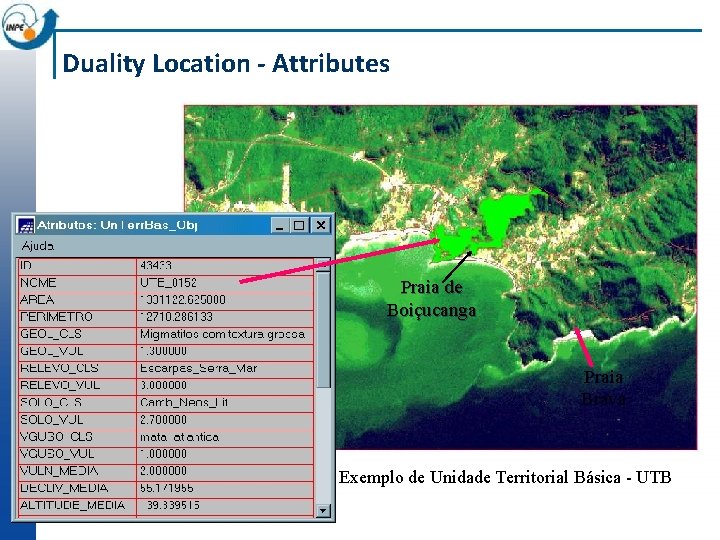
Duality Location - Attributes Praia de Boiçucanga Praia Brava Exemplo de Unidade Territorial Básica - UTB

Geometrical operations Point in Polygon = O(n)

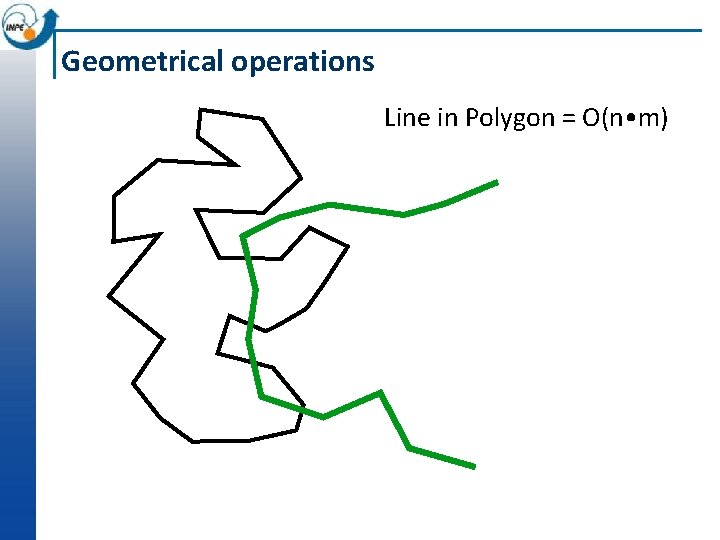
Geometrical operations Line in Polygon = O(n • m)

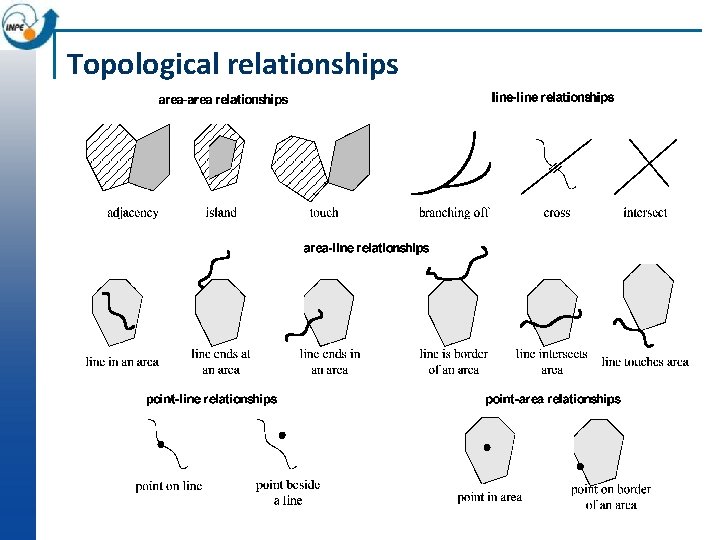
Topological relationships

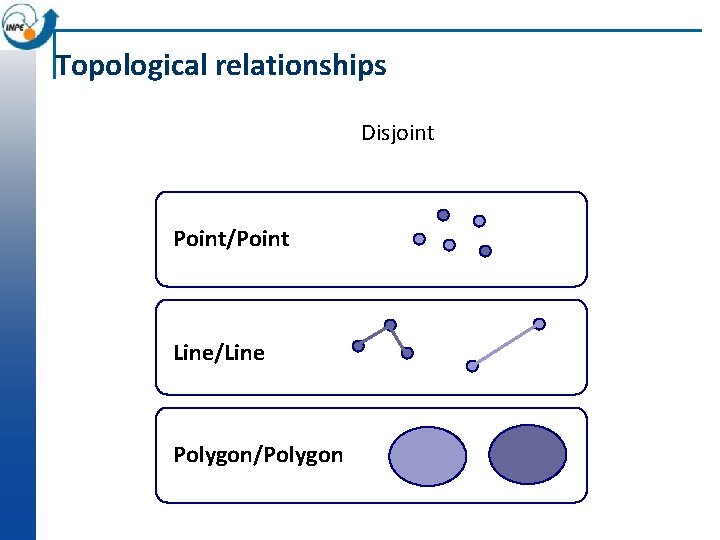
Topological relationships Disjoint Point/Point Line/Line Polygon/Polygon

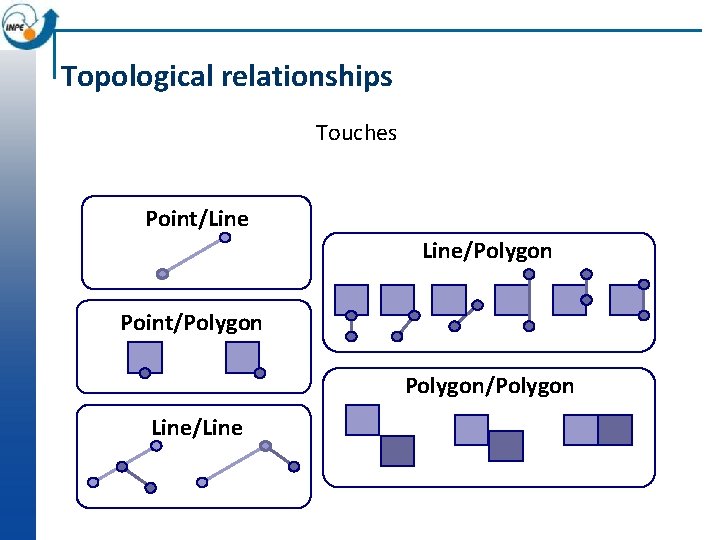
Topological relationships Touches Point/Line/Polygon Point/Polygon/Polygon Line/Line

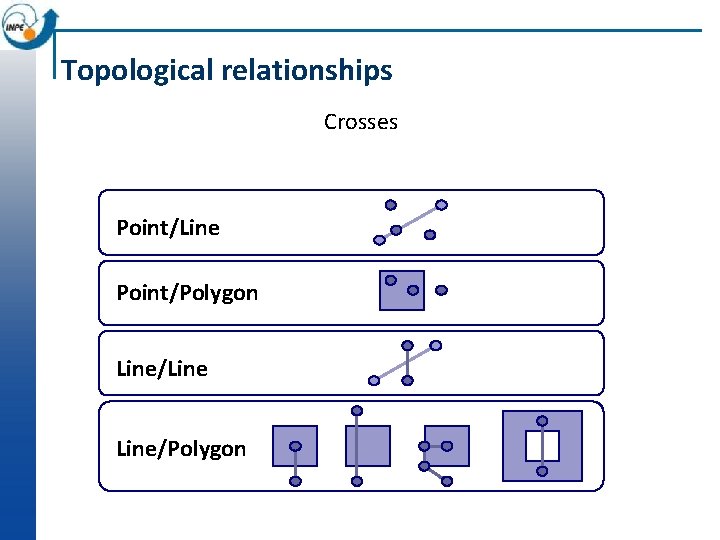
Topological relationships Crosses Point/Line Point/Polygon Line/Line/Polygon

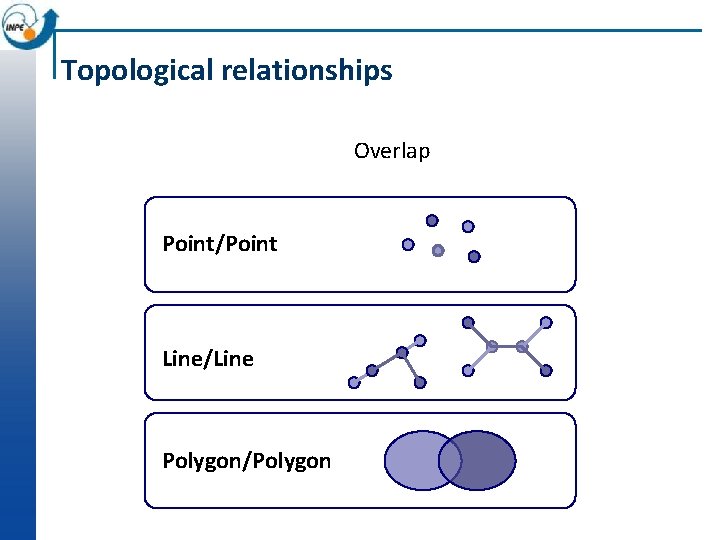
Topological relationships Overlap Point/Point Line/Line Polygon/Polygon

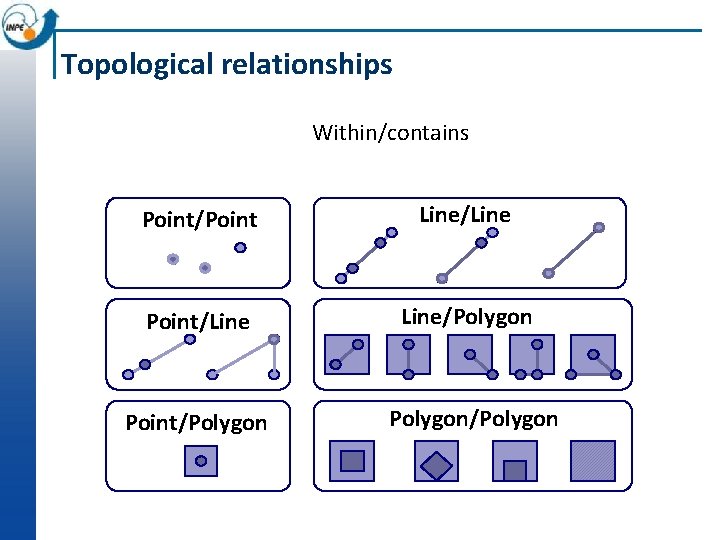
Topological relationships Within/contains Point/Point Line/Line Point/Line/Polygon Point/Polygon/Polygon

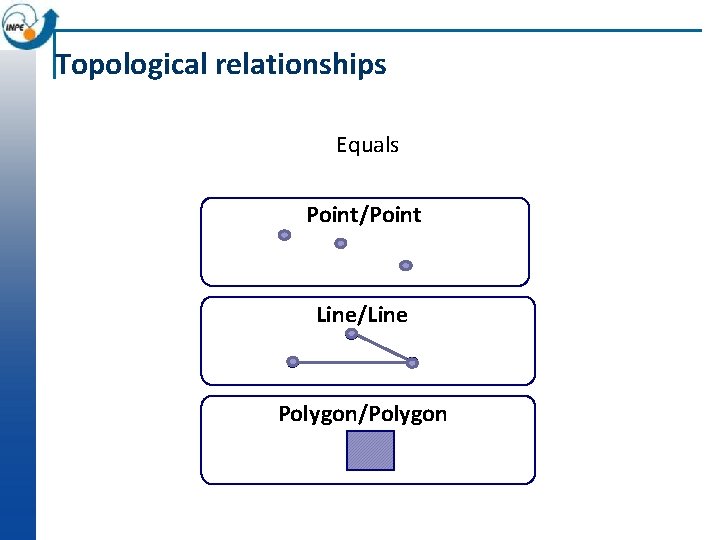
Topological relationships Equals Point/Point Line/Line Polygon/Polygon

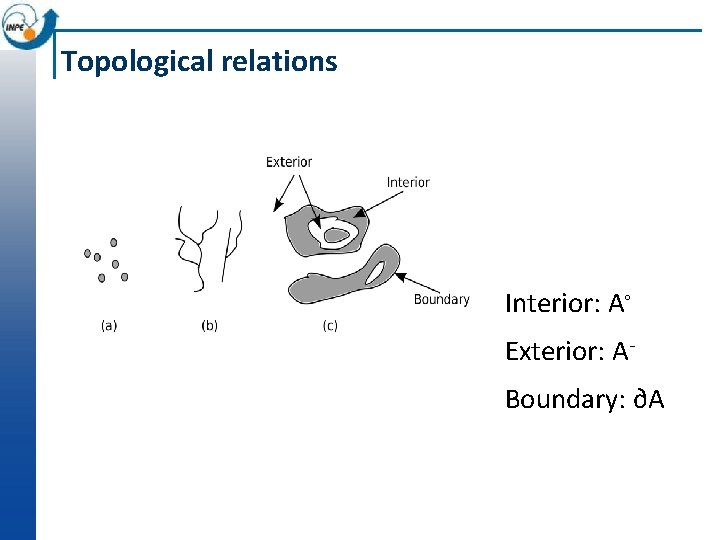
Topological relations Interior: A◦ Exterior: ABoundary: ∂A

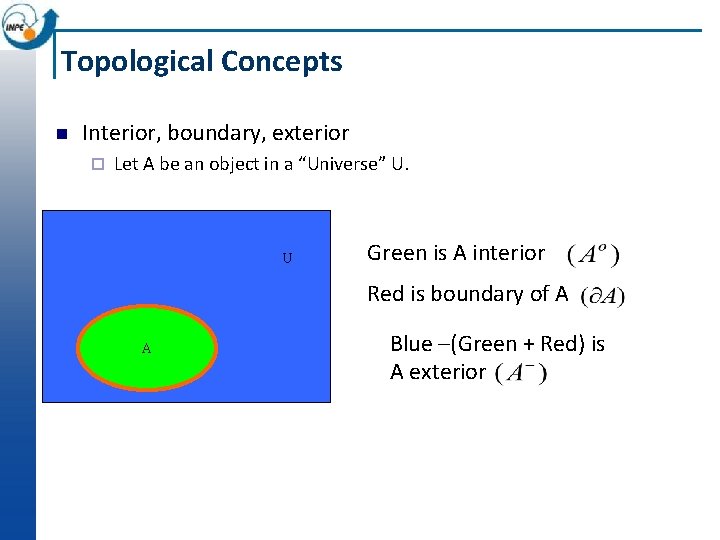
Topological Concepts n Interior, boundary, exterior ¨ Let A be an object in a “Universe” U. U Green is A interior Red is boundary of A A Blue –(Green + Red) is A exterior

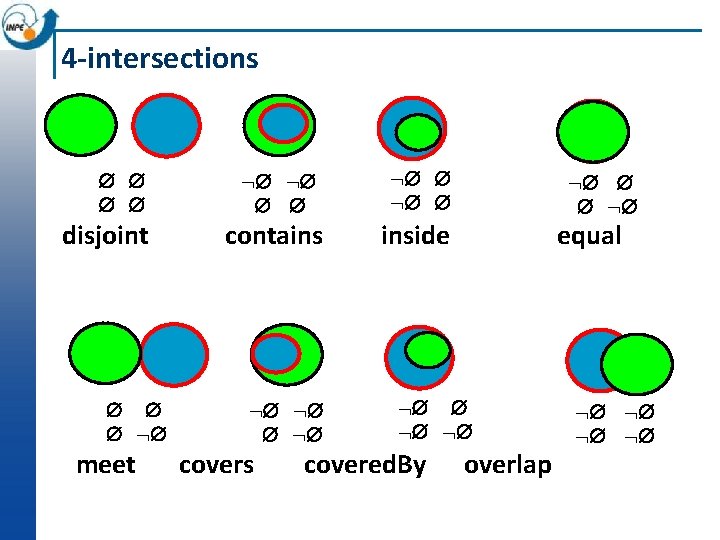
4 -intersections disjoint meet contains inside covers equal covered. By overlap

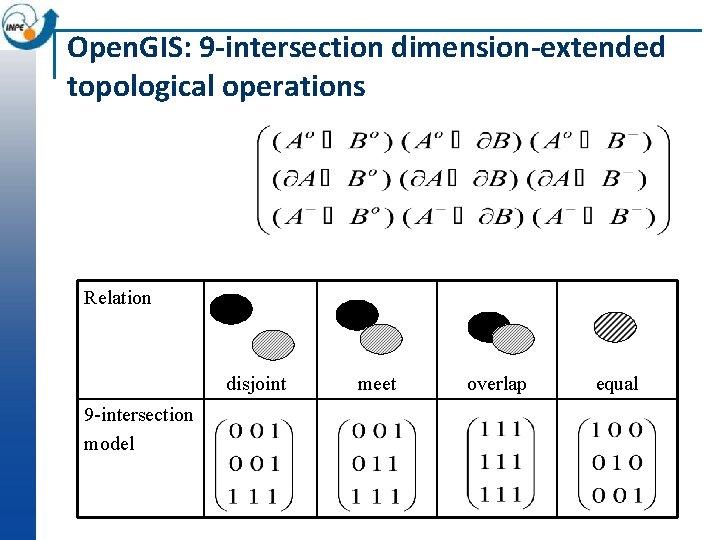
Open. GIS: 9 -intersection dimension-extended topological operations Relation disjoint 9 -intersection model meet overlap equal

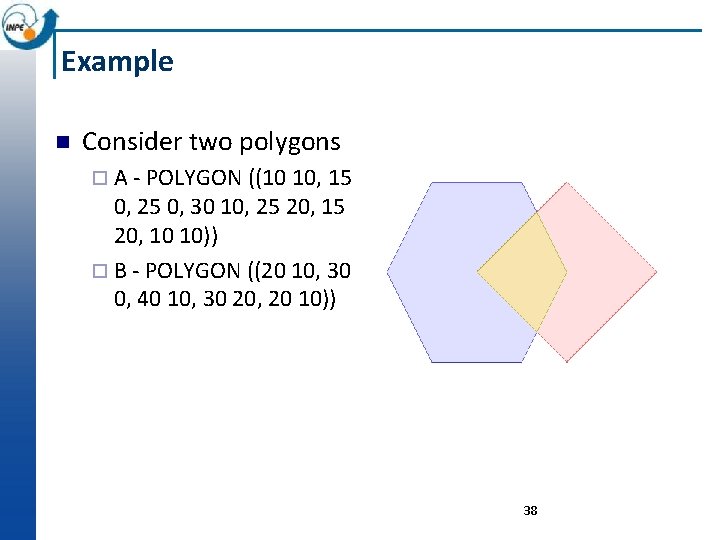
Example n Consider two polygons ¨ A - POLYGON ((10 10, 15 0, 25 0, 30 10, 25 20, 10 10)) ¨ B - POLYGON ((20 10, 30 0, 40 10, 30 20, 20 10)) 38

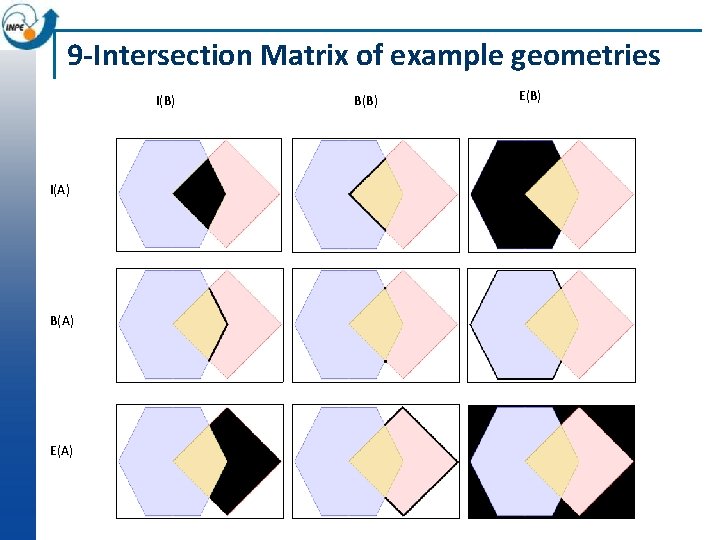
9 -Intersection Matrix of example geometries I(B) B(B) E(B) I(A) B(A) E(A) 39

Specifying topological operations in 9 Intersection Model Question: Can this model specify topological operation between a polygon and a curve?

9 -Intersection Model

DE-9 IM: dimensionally extended 9 intersection model 43

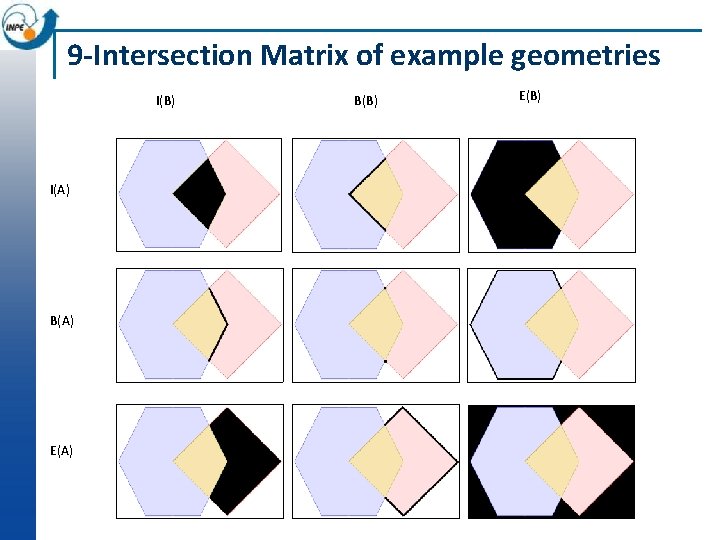
9 -Intersection Matrix of example geometries I(B) B(B) E(B) I(A) B(A) E(A) 44

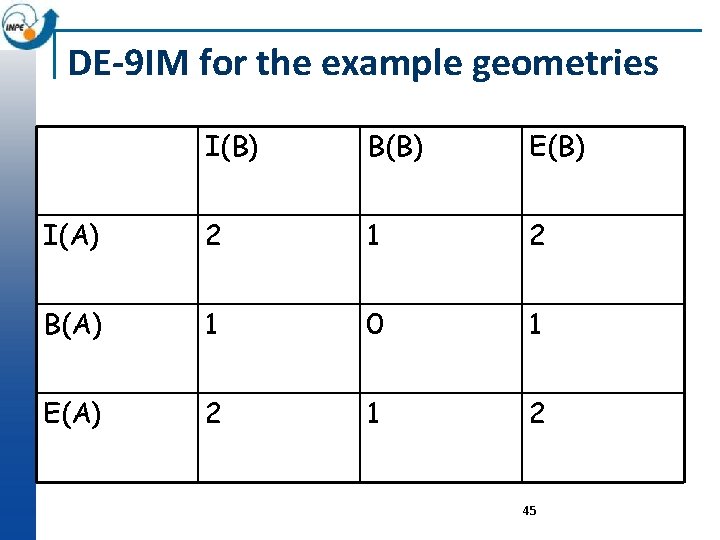
DE-9 IM for the example geometries I(B) B(B) E(B) I(A) 2 1 2 B(A) 1 0 1 E(A) 2 1 2 45

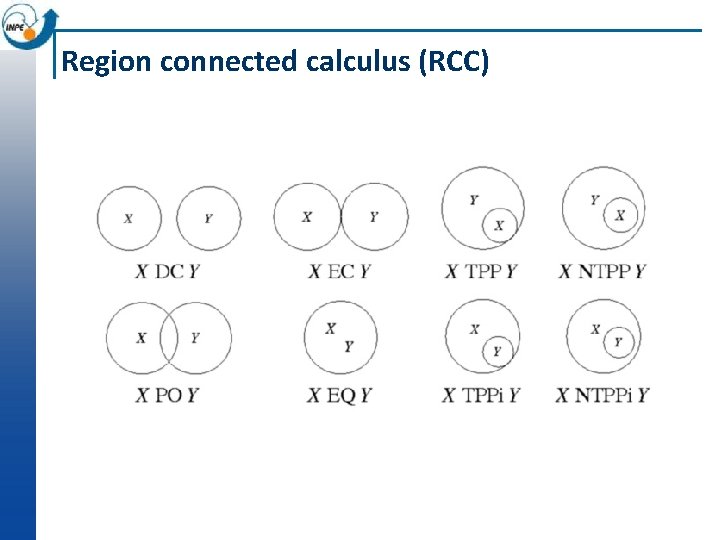
Region connected calculus (RCC)

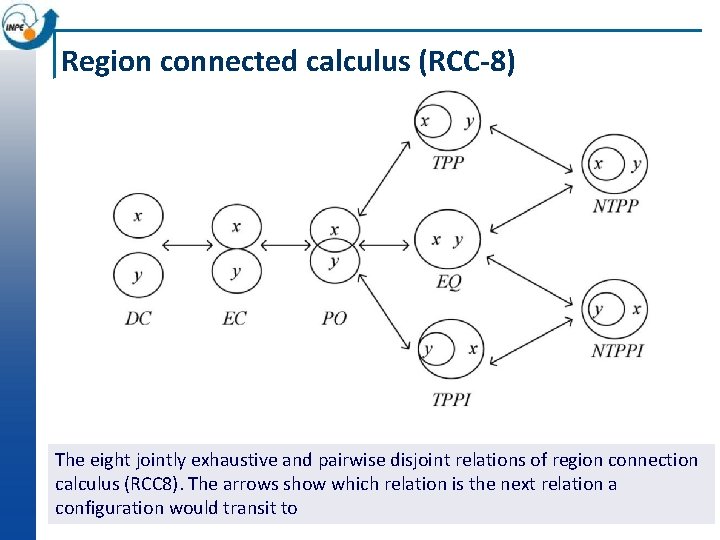
Region connected calculus (RCC-8) The eight jointly exhaustive and pairwise disjoint relations of region connection calculus (RCC 8). The arrows show which relation is the next relation a configuration would transit to