Introduo s Lgicas de Descries Fred Freitas CIn

Introdução às Lógicas de Descrições Fred Freitas CIn – UFPE fred@cin. ufpe. br

Sumário n Motivação – Problemas em frames e redes semânticas n n n Histórico Definições básicas Várias DLs Semântica Exemplos Mundo aberto n n n Web semântica Tarefas de raciocínio Reduções Tableaux Complexidade Outras soluções – Autômatos – Resolução n Comparação

Sumário n Motivação – Problemas em frames e redes semânticas n n n Histórico Definições básicas Várias DLs Semântica Exemplos Mundo aberto n n n Web semântica Tarefas de raciocínio Reduções Tableaux Complexidade Outras soluções – Autômatos – Resolução n Comparação

Tipos de formalismos de representação n Formalismos orientados a predicados: regras de produção e programação em lógica – Pioneiros - foco no processo, funcionamento n Formalismos orientados a domínios: frames, redes semânticas, lógica de descrições – Classes, relações e restrições – Facilitam a estruturação de conhecimento sobre um domínio de aplicação

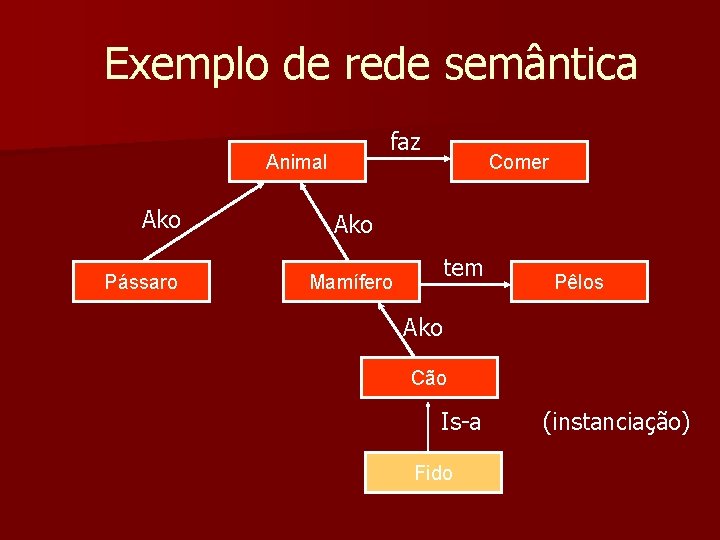
Exemplo de rede semântica faz Animal Ako Pássaro Comer Ako tem Mamífero Pêlos Ako Cão Is-a Fido (instanciação)

Expressividade dos Frames n Classes – Herança múltipla, – Instâncias n Atributos (slots) – Slots podem ser instâncias de outras classes (relações) n Facetas - Restrições sobre os slots – Valor default, valores permitidos (allowedvalues), domínio (ex: 1. . 100), cardinalidade máxima e mínima, tipo (inteiro, string, . . . ), . . .

Definindo classes e instâncias (defclass City "Cities are part of countries or states. " (is-a Location) (multislot is-Part-Of (type INSTANCE) (allowed-classes Country State) (inverse-slot has-Parts) (cardinality 1 1)) (single-slot name (type STRING) (cardinality 1 1))) ([Locations_00427] of City (is-Part-Of [WA]) (name "Washington"))

Problemas com RSs / frames: ambigüidade [Brachman 79, Franconi 2003] n entre classes e instâncias n em quantificação

Ambigüidade entre classes e instâncias n 29’er : n john : – – – – AGE : 29 , SEX : M, HEIGHT : Number , WIFE : Person.

Ambigüidade em quantificação [Franconi 2003] Sapo n tem-cor Verde O que signiifica? – – – Todo sapo é só verde Todo sapo também é verde Todo sapo é de algum tipo de verde Tem um sapo que é só verde. . . Sapos são tipicamente verdes, mas há exceções.

Conclusão: Problemas. . . n Falta de semântica formal – Interpretações ambíguas n Raciocínio depende do que o desenvolvedor pretende – Definições semelhantes levam a raciocínios bem diferentes Provadores de teoremas não eram necessários n Complexidade computacional depende de cada tipo de raciocínio n

n “It is unfortunately much easier to develop some algorithm that appears to reason over structures of a certain kind, than to justify its reasoning by explaining what the structures are saying about the domain. ”

Sumário n Motivação – Problemas em frames e redes semânticas n n n Histórico Definições básicas Várias DLs Semântica Exemplos Mundo aberto n n n Web semântica Tarefas de raciocínio Reduções Tableaux Complexidade Outras soluções – Autômatos – Resolução n Comparação

Histórico n 1ª. Geração (fins dos ’ 70 - 85) – Linguagens terminológicas – Representações com mais engajamento ontológico e semântica definida – Mais riqueza: papéis, classificação n Sistemas: – KL-ONE [Brachman & Schmolze 78] – KRYPTON [Brachman et al 83] § terminologia+regras § Tbox vs ABox

2ª. Geração – Sistemas com DL n Ênfase em teoria – Complexidade do raciocínio vs Expressividade – Identificação das fontes de complexidade – Uso de tableaux para raciocínio / classificação n Abordagens: – Limitada+completa: P § Ex: CLASSIC [Brachman 91] – uso industrial – Expressiva+incompleta: NP § Ainda ineficientes § Ex: LOOM [Mc. Gregor 87] e BACK [Nebel 90]

Nova (atual) geração n Alvo: Expressiva+completa! n Raciocínio baseado em tableaux, com otimizações n Estudo de relações com outras lógicas n Ex: FACT e RACER [Horrocks 98 e 2000] n Uso na Web semântica!

Sumário n Motivação – Problemas em frames e redes semânticas n n n Histórico Definições básicas Várias DLs Semântica Exemplos Mundo aberto n n n Web semântica Tarefas de raciocínio Reduções Tableaux Complexidade Outras soluções – Autômatos – Resolução n Comparação

Lógica de Descrições n Fragmento de L 2, Lógica de Predicados sem funções, com até 2 variáveis n Separação entre: – Terminologia (predicados): TBox – Asserções (constantes, instâncias): ABox n Representação sem variáveis – Interpretação como predicados, usando expressões- – Student x. Student(x)

Lógica de Descrições - Expressividade n Conceitos (predicados unários, classes, conjuntos de indivíduos, subconjunto do domínio) – Ex: Student – Ex: Married n {x|Student(x)} {x|Married(x)} Papéis (predicados binários, relações, conjuntos de pares de indivíduos) – Ex: friend {(x, y)|friend(x, y)} n Construtores para expressões de conceitos n Indivíduos (instâncias) – Ex: Student ⊓ has. Friend. Married – {x|Student(x)^ y(has. Friend(x, y)^Married(y))} – Ex: Student (zé), . . .

Lógica de Descrições - Intuição n Significado da restrição existencial – Ex: Student ⊓ has. Friend. Married – {x|Student(x)^ y(has. Friend(x, y)^Married(y))} n Sintaxe de Manchester – Student and has. Friend some Married

Sumário n Motivação – Problemas em frames e redes semânticas n n n Histórico Definições básicas Várias DLs Semântica Exemplos Mundo aberto n n n Web semântica Tarefas de raciocínio Reduções Tableaux Complexidade Outras soluções – Autômatos – Resolução n Comparação

Famílias de DLs S = FL- +AL*+ papéis transitivos – SHIQ

FL- (frame language) n Sintaxe n n n A : atomic- concept R : atomic- role C, D : concept n C, D A | C ⊓ D | R. C | R

Notação e Significado (Informal) R. C = indivíduos que estão na relação R e são do conceito C Interseção = conjunção n União = disjunção n Complemento = negação n

Bases de conhecimento n KB = Tbox + Abox n Tbox (Terminological part) = Descrições – Exemplos: § Student ≡ Person ⊓ studies. At. University § Phd. Student ⊑ Student ⊓ Researcher n Abox (Assertional part) – Instâncias – Exemplos: § Phd. Student (filipe) § studies. At (filipe, UFPE)

Descrições (axiomas) ⊑ enrolled. Course n Professor ⊑ teaches. Course n Working-student ⊑ Student n Working-student ⊑ Professor n Student – Pode ser um professor e/ou estudante – O mesmo que n As § Working-student ⊑ Student ⊔ Professor descrições sobre um item não são agrupadas como nos frames – Um classificador as organiza por raciocínio

Sumário n Motivação – Problemas em frames e redes semânticas n n n Histórico Definições básicas Várias DLs Semântica Exemplos Mundo aberto n n n Web semântica Tarefas de raciocínio Reduções Tableaux Complexidade Outras soluções – Autômatos – Resolução n Comparação

Semântica (“a la” Tarski) n

Interpretação n

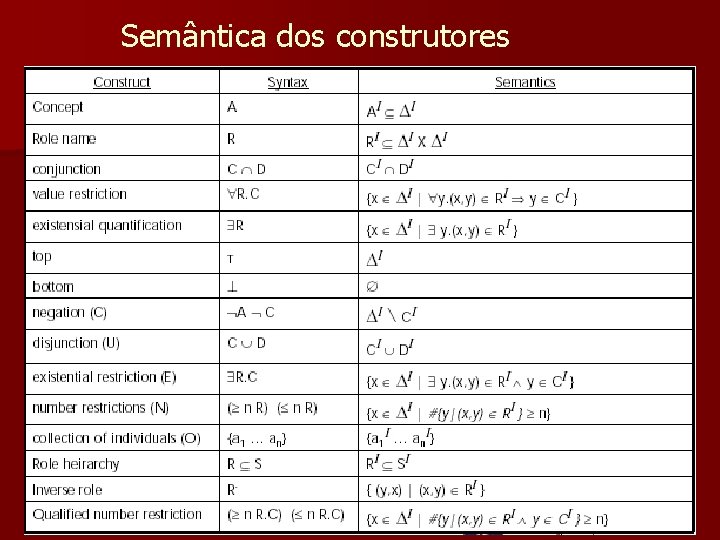
Semântica dos construtores

Sintaxe e Semântica das DLs

Lógica de Descrições - Intuição n Significado da restrição existencial – Ex: Student ⊓ has. Friend. Married – {x|Student(x)^ y(has. Friend(x, y)^Married(y))} n Sintaxe de Manchester – Student and has. Friend some Married n Significado da restrição universal – Ex: Student ⊓ ∀has. Friend. Married – {x|Student(x)^∀y(has. Friend(x, y) Married(y))} n Sintaxe de Manchester – Student and has. Friend only Married

Voltando aos batráquios. . . Sapo n tem-cor Verde Todo sapo é (de algum tipo de) verde – Sapo ⊑ tem-cor. Verde n Todo sapo é só (de algum tipo de) verde – Sapo ⊑ tem-cor. Verde n Tem um sapo que é verde – Sapo ( x ) , tem-cor ( x, verde. Musgo ) n. . .

Sumário n Motivação – Problemas em frames e redes semânticas n n n Histórico Definições básicas Várias DLs Semântica Exemplos Mundo aberto n n n Web semântica Tarefas de raciocínio Reduções Tableaux Complexidade Outras soluções – Autômatos – Resolução n Comparação

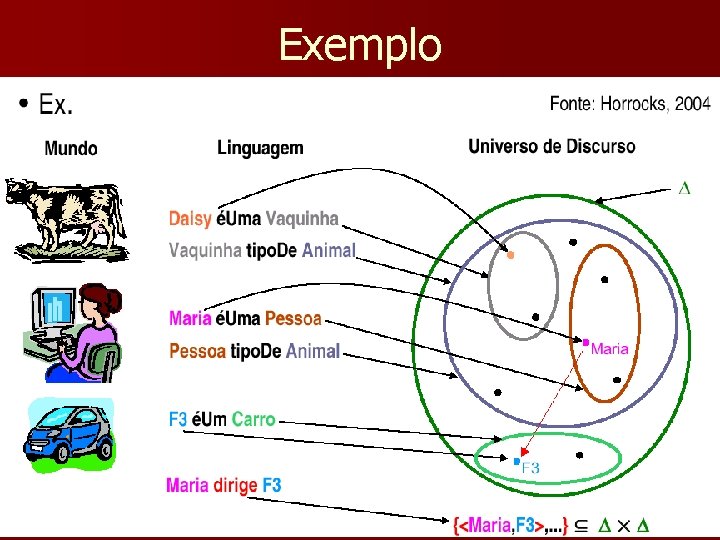
Exemplo

Exemplo (cont. ) n

Exemplo [Baader 2012] n Suponha que tenhamos as instâncias: ?

Exemplo [Baader 2012] n Suponha que tenhamos as instâncias:

Base de Conhecimento em DL n Uma ontologia em DL é uman A TBox tem axiomas para Base de conhecimento - S = <TBox, ABox> n A ABox tem axiomas de instanciação de – Conceitos § x D – Papéis § <x, y> r § (Student U Professor)(paul) – Conceitos: § C ⊑ D (inclusão) § C D (equivalência) – Papéis (ou propriedades): § § R S (inclusão) R = S (equivalência) R = S o T (composição) R+ R (transitividade) – nem toda DL tem…

Bases de conhecimento n Condições necessárias são expressas com ⊑ n Condições necessárias e suficientes são expressas com – Teaching-Assistant Undergrad ⊔ Professor n Para uma interpretação satisfazer uma ontologia (base de conhecimento) – Precisa satisfazer TBox e ABox – Então ela é um modelo desta ontologia n Uma ontologia é satisfatível se admite um modelo

Exemplo - Subsunção n

Famílias de DLs S = FL- +AL*+ papéis transitivos – SHIQ

ALC (DL atributiva) e FL’s n AL = FL- (DL estrutural) + negação – DL proposicional n FL 0 = FL- + R. C (no lugar de R, que é R. T) – Interpretação de R é a mesma de R. C, sem CI(y) n ALC = FL 0 + negação (complemento)

Outras ALs n U – União (disjunção) – Human Male U Female E – quantificação existencial ( R. C) n N – restrições numéricas (de cardinalidade) sobre papéis ( R, R) n – – – Busy-Woman ⊓ ( 3 child) Conscious-Woman ⊓ ( 5 child) 1 R R EU = C (U e E podem ser obtidos de FL- +C) n Estudadas: ALC (ou ALUE) e ALCN (ou ALUEN) n

O Q de SHIQ – restrições numéricas (de cardinalidade) sobre papéis qualificados ( R. C, R. C) n. Q – Worried-Woman ⊓ ( 3 child. Man) n Note que U, E, N, C, Q e interseção são construtores de classes

Classificação n Colocar um conceito/papel no devido lugar dentro da hierarquia, de forma a que – Abaixo dele, esteja o conceito mais geral que é mais específico que ele – Acima dele, esteja o conceito mais específico que é mais geral que ele n Verifica estas relações por subsunção – Quais conceitos “cabem”dentro de quais

Sumário n Motivação – Problemas em frames e redes semânticas n n n Histórico Definições básicas Várias DLs Semântica Exemplos Mundo aberto n n n Web semântica Tarefas de raciocínio Reduções Tableaux Complexidade Outras soluções – Autômatos – Resolução n Comparação

Sobre o Raciocínio n Basicamente por subsunção (herança) – Checar se um conceito/papel é contido por outro n Hipótese do Mundo Aberto – Em contraste com quase todos os outros formalismos de representação (Mundo Fechado) – Em Frames, Presidente tem cardinalidade 1 – Presidente(Lula), Presidente(Líder-Sindical) dará erro – Um classificador DL, conclui que Lula e Líder-Sindical são a mesma pessoa

Cuidados com mundo aberto [Rector et al 2004] Margheritta≡ Pizza ⊓ ∃has_topping. Mozza ⊓ ∃has_topping. Tomato 49

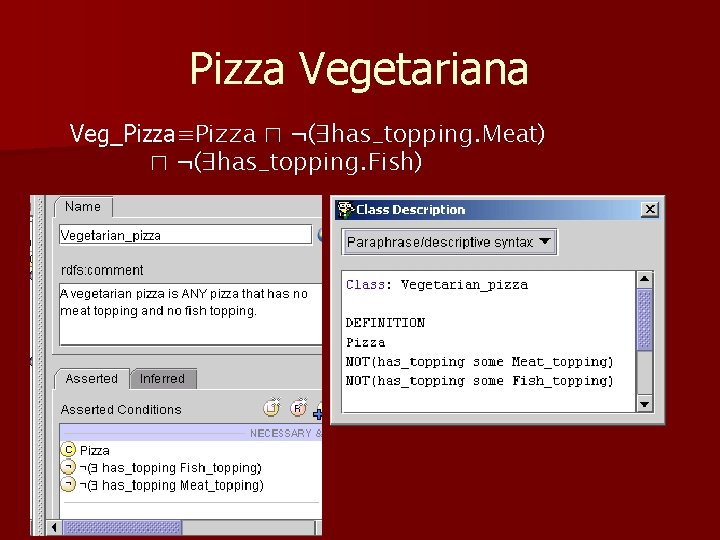
Pizza Vegetariana Veg_Pizza≡Pizza ⊓ ¬(∃has_topping. Meat) ⊓ ¬(∃has_topping. Fish) 50

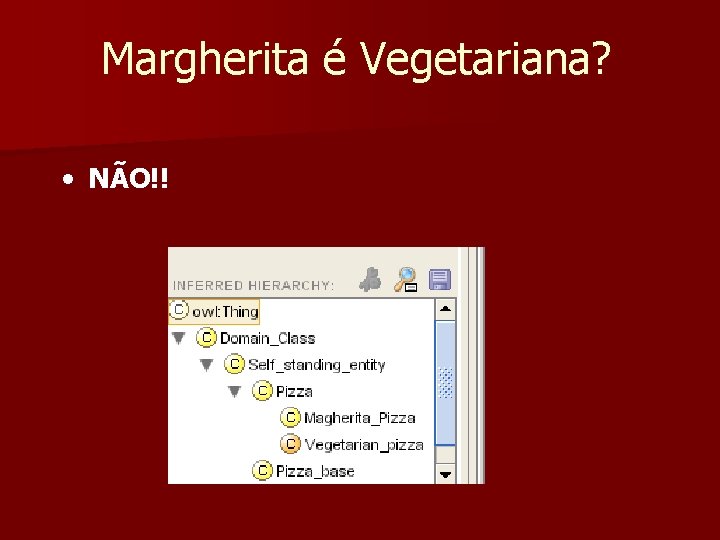
Margherita é Vegetariana?

Margherita é Vegetariana? • NÃO!!

Por quê? n “A vegetarian pizza is any pizza that, amongst other things, does not have any meat topping and does not have any fish topping” n “A margherita pizza is a pizza and, amongst other things, has some tomato topping and has some mozarella topping”

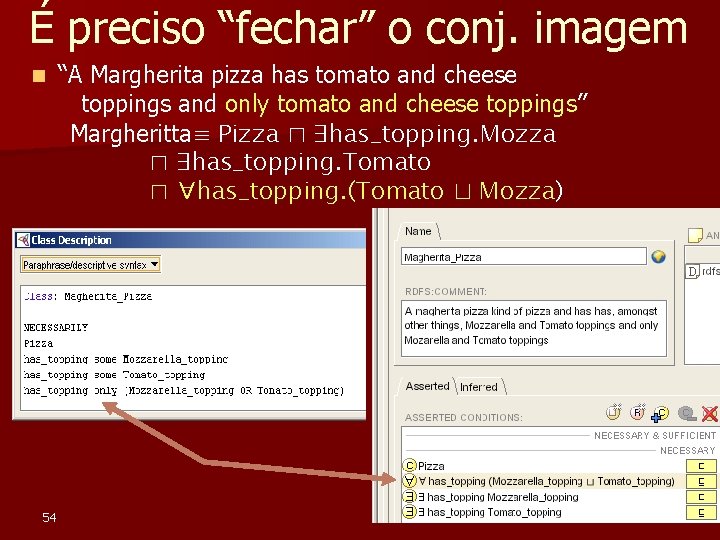
É preciso “fechar” o conj. imagem n 54 “A Margherita pizza has tomato and cheese toppings and only tomato and cheese toppings” Margheritta≡ Pizza ⊓ ∃has_topping. Mozza ⊓ ∃has_topping. Tomato ⊓ ∀has_topping. (Tomato ⊔ Mozza)

Classificação correta, agora n Meat , Mozza e Tomato precisam ser disjuntos 55

Porque DL foi adotada pela Web Semântica?

Várias causas. . . n Por causa da Hipótese de Mundo Aberto – Não se pode assumir que, se um fato não foi encontrado na Web, então ele não existe n Igualdade de indivíduos é possível – A dedução ou representação de que no exemplo anterior Lula = Líder-Sindical n Representação lógica sem variáveis em tese facilita o entendimento por usuários

OWA vs. CWA [Staab 2006] OWA: Open World Assumption (Mundo Aberto) A existência de mais indivíduos é possível a não ser que isto seja explicitamente colocado. OWL uses OWA! CWA: Closed World Assumption (Mundo Fechado) Assume-se que a base de conheciemtno contém todos os individuos que existem e todos os facts. Todos os filhos de Bill são homens? child(Bill, Bob) Man(Bob) 1 child. T(Bill) Não se sabe, pois não se conhecem todos os filhos de Bill Assumindo que sabemos tudo sobre Bill, todos os seus filhos são homens. ? ⊨ child. Man(Bill) DL Não se sabe Prolog sim ? ⊨ child. Man(Bill) sim Agora sabemos tudo sobre os filhos de Bill em DL.

Do ponto de vista de raciocínio n. A classificação é boa para a Web pois as informações encontram-se espalhadas n É preciso ainda garantir o raciocínio – Lógica de 1ª ordem é semi-decidível – Hoje, em OWL 2, as DLs são decidíveis

Exemplo em OWL [Horrocks 2004] Ontologies Dr. Ancestor ≡ Person ⊓ ∃has. Child. (Dr ⊔ ∃has. Child. Dr) <owl: Class rdf: ID=“Dr. Ancestor”> <owl: intersection. Of rdf: parse. Type=" collection"> <owl: Class rdf: about="#Person"/> <owl: Restriction> <owl: on. Property rdf: resource="#has. Child"/> <owl: to. Class> <owl: union. Of rdf: parse. Type=" collection"> <owl: Class rdf: about="#Dr"/> <owl: Restriction> <owl: on. Property rdf: resource="#has. Child"/> <owl: has. Class rdf: resource="#Dr"/> </owl: Restriction> </owl: union. Of> </owl: to. Class> </owl: Restriction> </owl: intersection. Of> </owl: Class>

Referências n The Description Logic Handbook. F. Baader et al. 2003. Cambridge Press. n Curso de DL. Enrico Franconi, Univ. Bozen. Bolzano, Itália. n Curso de Ontologias. Virgínia Brilhante, UFAM.

Bibliografia n NARDI, D. ; BRACHMAN, R. “An Introduction to Description Logics”. In: The Description Logic Handbook – Theory, Implementation and Applications. Editedy by Franz Baader, Diego Calvanese, Deborah Mc. Guinness, Daniele Nardi and Peter Patel. Schneider, 2003. n BAADER, F. ; NUTT, W. “Basic Description Logics”. In: The Description Logic Handbook – Theory, Implementation and Applications. Editedy by Franz Baader, Diego Calvanese, Deborah Mc. Guinness, Daniele Nardi and Peter Patel-Schneider, 2003. n BAADER, F. “Description Logic Terminology”. In: The Description Logic Handbook – Theory, Implementation and Applications. Editedy by Franz Baader, Diego Calvanese, Deborah Mc. Guinness, Daniele Nardi and Peter Patel-Schneider, 2003.

Bibliografia n HORROCKS, I. “Implementation and Optimisation Techniques”. In: The Description Logic Handbook – Theory, Implementation and Applications. Editedy by Franz Baader, Diego Calvanese, Deborah Mc. Guinness, Daniele Nardi and Peter Patel. Schneider, 2003 a. n VIEIRA, R. ; ABDALLA, D. ; SILVA, D. M. ; SANTANA, M. R. “Web Semântica: Ontologias, Lógicas de Descrições e Inferências”. In: Web e Multimídia: Desafios e Soluções. PUC Minas, 2005.