INTRODUO PESQUISA OPERACIONAL Programao Linear Parte 2 Profa

INTRODUÇÃO À PESQUISA OPERACIONAL ** Programação Linear – Parte 2 ** Profa. Vitória Pureza 2º Semestre

Última Aula • Exemplo de modelagem matemática • Resolução Gráfica de Problemas de 2 Variáveis • Casos de Programação Linear: Uma única solução ótima, Soluções Ótimas Alternativas, PL infactível, e PL ilimitado • Uma implicação da Premissa de Linearidade: pelo menos uma das soluções ótimas* estão em vértices da região factível • Transformação de Problemas de Programação Linear na Forma Padrão • Nesta aula vamos aprender o método Simplex para resolução de PLs

Roteiro • Método Simplex em Tabelas • Aplicando o Algoritmo Simplex a Problemas de Maximização • O Método Simplex e PLs Ilimitados • O Método Simplex e Soluções Ótimas Alternativas • Degenerescência em PLs • Dificuldades em PLs Degenerados • Determinação de Soluções Básicas Factíveis Iniciais • Relações entre PLs e os Problemas Artificiais Associados

Problemas com mais de 2 variáveis Método Simplex Visita pontos extremos um até que condições de otimalidade sejam satisfeitas

Método Simplex em tabelas As operações realizadas no método simplex podem ser organizadas em tabelas, denominadas tabelas simplex Embora não seja a melhor forma de se implementar o método em um computador, esta organização pode ser interessante para manipular problemas pequenos e compreender mais rapidamente como o método funciona Considere o problema de otimização linear na forma padrão Minimizar f(x) = c. T x Ax = b x 0

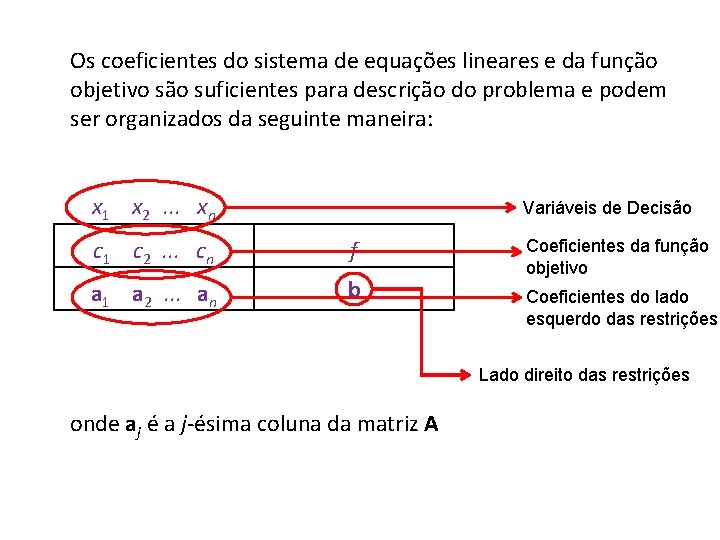
Os coeficientes do sistema de equações lineares e da função objetivo são suficientes para descrição do problema e podem ser organizados da seguinte maneira: x 1 x 2 . . . xn c 1 c 2 . . . cn a 1 a 2 . . . an Variáveis de Decisão f b Coeficientes da função objetivo Coeficientes do lado esquerdo das restrições Lado direito das restrições onde aj é a j-ésima coluna da matriz A

Exemplo: Minimizar f(x 1, x 2) = x 1 2 x 2 x 1 + x 2 ≤ 6 x 1 x 2 ≤ 4 x 1 + x 2 ≤ 4 x 1 ≥ 0, x 2 ≥ 0 Adicionando as variáveis de folga x 3, x 4 e x 5, obtêm-se a forma padrão Minimizar f(x 1, x 2) = x 1 2 x 2 + 0 x 1 + 0 x 2 + 0 x 3 x 1 + x 2 + x 3 = 6 x 1 x 2 + x 4 = 4 x 1 + x 2 + x 5 = 4 x 1 ≥ 0, x 2 ≥ 0, x 3 ≥ 0, x 4 ≥ 0, x 5 ≥ 0

Exemplo: Minimizar f(x 1, x 2 , x 3, x 4, x 5) = x 1 2 x 2 + 0 x 1 + 0 x 2 + 0 x 3 x 1 + x 2 + x 3 = 6 x 1 x 2 + x 4 = 4 x 1 + x 2 + x 5 = 4 x 1 ≥ 0, x 2 ≥ 0, x 3 ≥ 0, x 4 ≥ 0, x 5 ≥ 0 Os coeficientes do sistema Ax = b e da função objetivo f(x)=c. Tx são apresentados na tabela x 1 x 2 x 3 x 4 x 5 1 2 0 0 0 f 1 1 1 0 0 6 1 1 0 4 1 1 0 0 1 4 Note que as colunas das variáveis x 3, x 4, x 5 formam uma matriz identidade - estas variáveis são chamadas de variáveis básicas

• Numa tabela simplex, a matriz dos coeficientes das variáveis básicas é sempre a matriz identidade • Isto significa que cada variável básica está expressa em termos das demais variáveis, no caso, x 1 e x 2, as quais são chamadas de variáveis não básicas Assim, basta atribuir valores às variáveis não básicas x 1 e x 2 para que tenhamos uma solução que satisfaça o sistema Ax = b Para o exemplo, tem-se: x 3 = b 1 a 11 x 1 a 12 x 2 = 6 x 1 x 2 x 4 = b 2 a 21 x 1 a 22 x 2 = 4 x 1 + x 2 x 5 = b 3 a 13 x 1 a 32 x 2 = 4 + x 1 x 2

Se fixarmos, por exemplo, as variáveis não básicas x 1 e x 2 em seus limites inferiores (x 1, x 2 ≥ 0, portanto, zero é o limite de ambas). . . então as demais variáveis têm valores x 3 = 6 x 1 x 2 = 6 x 4 = 4 x 1 + x 2 = 4 x 5 = 4 + x 1 x 2 = 4 e produzem uma solução factível para o problema cujo valor é f = 0 Esta solução básica corresponde a um vértice da região factível (S) indicado abaixo

Como as variáveis não básicas x 1 e x 2 estão em seus limites inferiores, a única possibilidade de examinar soluções alternativas consiste em aumentar os valores de x 1 e x 2 Note que: o A função objetivo é f = x 1 2 x 2 o Em soluções alternativas resultantes do aumento de x 1 ou x 2, a função objetivo decresce (melhora), ou seja, a solução básica atual (x 1 = 0, x 2 = 0, x 3 = 6, x 4 = 4, x 5 = 4) não é ótima Consideremos a alteração de uma variável não básica por vez (estratégia simplex)

Aumento do valor de x 2, mantendo-se x 1 = 0 o a função objetivo decresce com a taxa de variação 2 (f = 2 x 2) e quanto maior o valor de x 2, menor será o valor de f o Com o aumento de x 2, os valores das variáveis básicas (x 3, x 4, x 5) são alterados, podendo aumentar ou diminuir desde que a não negatividade das variáveis seja preservada § x 3 = b 1 a 12 x 2 = 6 x 2 0 (a 12 = 1) como a 12 > 0, então b 1 a 12 x 2 0, , e portanto, x 2 6 § x 4 = b 2 a 22 x 2 = 4 + x 2 0 (a 22 = -1) como a 22 < 0, então a variável x 4 cresce com x 2, não limitando o aumento em x 2 § x 5 = b 3 a 32 x 2 = 4 x 2 0 (a 32 = 1) como a 32 > 0, então b 3 a 32 x 2 0, , e portanto, x 2 4 Apenas as variáveis básicas x 3 e x 5 limitam o crescimento de x 2

• Note que se a 12 0, a 22 0 e a 32 0, então a variável x 2 poderia crescer indefinidamente e f , e o problema não teria solução ótima finita (PL ilimitado) O maior valor possível para x 2 é 4, ou seja, x 2 = mínimo{ } = 4 e, com este valor, segue que: x 5 = 4 x 2 = 0 (a variável da terceira restrição se anula) Isto produz uma nova solução: Variáveis não básicas: x 1 = 0, x 2 = 4 Variáveis básicas: x 3 = 2, x 4 = 8, x 5 = 0 Valor da função objetivo: f = 0 – 2 x 2 = 8

Variáveis não básicas são agora redefinidas como aquelas cujo valores são nulos, enquanto variáveis básicas tem valores positivos Assim, dizemos que a variável não básica x 2 “entrou na base” no lugar da variável básica x 5 que “saiu da base” x 2 passa a ser a variável básica da terceira equação • Note que tínhamos uma solução básica factível com valor f = 0 . . . agora temos outra solução básica factível melhor com valor f = 8 Entretanto, as colunas das novas variáveis básicas não formam a matriz identidade: a tabela simplex precisa ser pivotada para que isso ocorra Este procedimento, que parte de uma solução básica factível e obtém outra melhor, consiste em uma iteração do método simplex

Iteração do método simplex usando tabelas i. Encontre uma variável não básica xk que tenha o coeficiente negativo na função objetivo: xk é candidata a entrar na base ii. Percorra a coluna na tabela simplex da variável xk e, para cada coeficiente positivo (aik > 0), calcule: • (valores que anulam a variável básica na linha i) • e faça iii. Com , a variável básica da linha se anula (i. e. , a variável básica da linha sai da base) iv. Se 0, i = 1, . . . , m, então f e o problema não tem solução ótima finita (pare) v. Redefina as variáveis básicas e não básicas e pivote a tabela simplex para esta nova solução básica

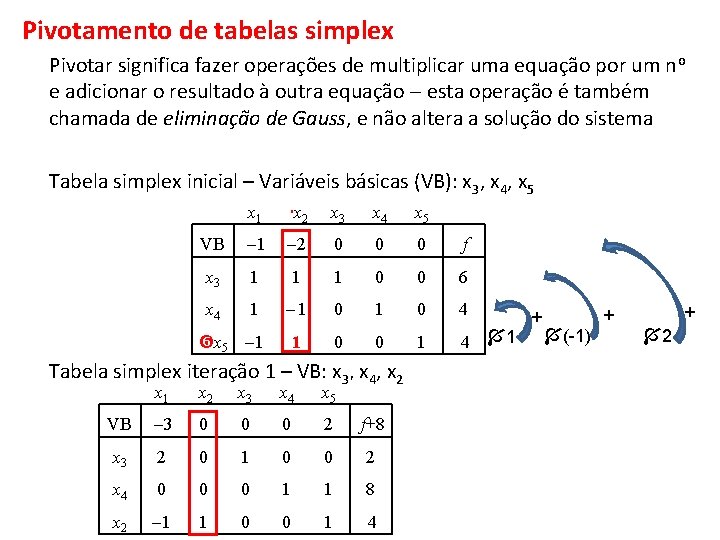
Pivotamento de tabelas simplex Pivotar significa fazer operações de multiplicar uma equação por um no e adicionar o resultado à outra equação esta operação é também chamada de eliminação de Gauss, e não altera a solução do sistema Tabela simplex inicial – Variáveis básicas (VB): x 3, x 4, x 5 x 1 x 2 x 3 x 4 x 5 VB 1 2 0 0 0 f x 3 1 1 1 0 0 6 x 4 1 1 0 4 x 5 1 1 0 0 1 Tabela simplex iteração 1 – VB: x 3, x 4, x 2 4 x 1 x 2 x 3 x 4 x 5 VB 3 0 0 0 2 f+8 x 3 2 0 1 0 0 2 x 4 0 0 0 1 1 8 x 2 1 1 0 0 1 4 1 + + + (-1) 2

A linha da função objetivo significa f + 8 = 3 x 1 + 2 x 5 ou f = 8 3 x 1 + 2 x 5 Os coeficientes das variáveis não básicas na função objetivo são chamados custos + 1 relativos

Exercício: Faça uma nova iteração para o problema x 1 x 2 x 3 x 4 x 5 VB 3 0 0 0 2 f+8 x 3 2 0 1 0 0 2 x 4 0 0 0 1 1 8 x 2 1 1 0 0 1 4 • Note que aumentar o valor da variável x 1, mantendo-se x 5 = 0, faz decrescer a função objetivo na taxa 3 (custo relativo de x 1) • As equações do sistema mostram que com x 5 = 0: o x 3 = 2 2 x 1 0 o x 4 = 8 + 0 x 1 0 o x 2 = 4 + x 1 0 O valor máximo para x 1 é 1 • Com este valor para x 1, a variável básica na primeira equação x 3 = 2 2 x 1 se anula, enquanto a variável não básica x 1 torna-se positiva • Isto fornece uma nova solução básica: Variáveis não básicas: x 1 = 1, x 5 = 0 Variáveis básicas: x 3 = 0, x 4 = 8, x 2 = 5 Valor da função objetivo: f = – x 1 – 2 x 2 = – 11

• As variáveis não básicas são agora redefinidas como aquelas cujos valores são zero e as variáveis básicas como aquelas cujos valores são positivos: Variáveis não básicas: x 3 = 0, x 5 = 0 Variáveis básicas: x 1 = 1, x 4 = 8, x 2 = 5 • Como a variável x 1 entrou na base (primeira coluna) e a variável x 3 saiu da base (primeira equação), uma nova tabela simplex é reescrita com pivotamento Tabela simplex iteração 1 – VB: x 3, x 4, x 2 x 1 x 2 x 3 x 4 x 5 f+8 VB 3 0 0 0 2 f+8 0 2 1/2 x 3 1 0 1/2 0 0 1 1 1 8 x 4 0 0 0 1 1 8 0 1 4 x 2 1 1 0 0 x 1 x 2 x 3 1 x 4 4 x 5 x 1 x 2 x 3 x 4 x 5 VB 3 0 0 0 2 x 3 2 0 1 0 x 4 0 0 0 x 2 1 1 0 Tabela simplex iteração 2 – VB: x 1, x 4, x 2 3 + 1 + VB 0 0 3/2 f+11 x 1 1 0 1/2 0 -1/2 1 x 4 0 0 0 1 1 8 x 2 0 1 1/2 0 1/2 5

Note que f = 11 + 3/2 x 3 + 3/2 x 5 Note também que os custos relativos das variáveis não básicas são positivos sua introdução na base aumentaria (pioraria) f Portanto, a solução x 1=1, x 2=5 e x 4=8 (f=11) é ótima 1/2 Quando todos os custos relativos são negativos (maiores ou iguais a zero), dizemos que a condição de otimalidade foi satisfeita

O algoritmo Simplex (em tabelas) Seja um problema de otimização linear escrito na forma padrão Fase I: Determine uma tabela simplex inicial, isto é, 1. A matriz dos coeficientes contém uma matriz identidade m m (m é o número de equações) e o vetor independente b 0 2. A função objetivo é escrita em termos das variáveis não básicas, isto é, os coeficientes das variáveis básicas são nulos 3. Faça iteração = 0 Fase II: 1. Obtenha o menor dos custos relativos (regra de Dantzig) : ck = mínimo {cj para toda variável não básica}. 2. Se ck 0, então pare (a solução básica é ótima). C. c. , a variável xk entra na base 3. Se aik 0, i = 1, . . . , m, pare (não existe solução ótima finita). C. c. , determine (a variável básica da linha sai da base). 4. Faça pivotamento no elemento (l, k). A variável xk passa a ser a variável básica na linha. Faça iteração = iteração + 1 e retorne ao passo 1

O Método Simplex e PLs Ilimitados Seja o problema Minimizar f(x 1, x 2) = x 1 x 2 4 x 1 + x 2 4 x 1 0, x 2 0 • Introduzindo-se as variáveis de folga, a matriz identidade é formada pelas colunas das variáveis x 3 e x 4; como o vetor de recursos b é não negativo, tem-se a tabela simplex inicial: x 1 x 2 x 3 x 4 0 0 f VB 1 1 Tabela simplex inicial – VB: x 3, x 4 1 1 1 0 4 1 0 x 4 1 A variável x 1 entra na base e a variável x 3 sai da base 1 4 x 3

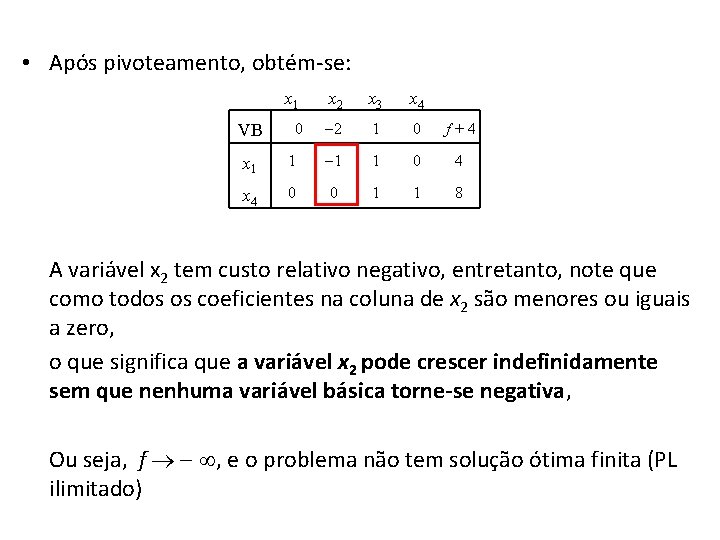
• Após pivoteamento, obtém-se: VB x 1 x 2 0 2 x 3 x 4 1 0 f+4 x 1 1 0 4 x 4 0 0 1 1 8 A variável x 2 tem custo relativo negativo, entretanto, note que como todos os coeficientes na coluna de x 2 são menores ou iguais a zero, o que significa que a variável x 2 pode crescer indefinidamente sem que nenhuma variável básica torne-se negativa, Ou seja, f , e o problema não tem solução ótima finita (PL ilimitado)

Aplicando o Algoritmo Simplex a Problemas de Maximização Opção 1) Transforme-o em um problema de minimização e o resolva conforme demonstrado Opção 2) Modifique os passos 2 e 3 da fase 2 como se segue: 1. Obtenha o maior dos custos relativos: ck = máximo {cj para toda variável não básica}. 2. Se ck ≤ 0, então pare (a solução básica é ótima). C. c. , a variável xk entra na base

Lista 2: Aplique o método Simplex aos seguintes PLs 1) Maximizar f(x 1, x 2, x 3) = 60 x 1 + 30 x 2 + 20 x 3 8 x 1 + 6 x 2 + x 3 48 4 x 1 + 2 x 2 + 1, 5 x 3 20 2 x 1 + 1, 5 x 2 + 0, 5 x 3 8 x 2 5 x 1 ≥ 0, x 2 ≥ 0, x 3 ≥ 0 2) Maximizar f(x 1, x 2, x 3) = 60 x 1 + 35 x 2 + 20 x 3 8 x 1 + 6 x 2 + x 3 48 4 x 1 + 2 x 2 + 1, 5 x 3 20 2 x 1 + 1, 5 x 2 + 0, 5 x 3 8 x 2 5 x 1 ≥ 0, x 2 ≥ 0, x 3 ≥ 0 3) Maximizar f(x 1, x 2, x 3, x 4) = 36 x 1 + 30 x 2 – 3 x 3 – 4 x 4 x 1 + x 2 – x 3 5 6 x 1 + 5 x 2 – x 4 10 x 1 0, x 2 0, x 3 0, x 4 0

Solução: 1) x*=(2, 0, 8) , f*(x) = 280 2) x*=(2, 0, 8) , f*(x) = 280 3) PL ilimitado

O Método Simplex e Soluções Ótimas Alternativas Em um PL min: • Se todas as variáveis não básicas na tabela simplex ótima tiverem custos relativos positivos, então o PL tem uma solução ótima única • Se alguma variável não básica tiver custo relativo igual a zero, então é possível que o PL tenha soluções alternativas ótimas Considere o seguinte PL Minimizar f(x 1, x 2) = x 1 x 2 x 1 + x 2 6 x 1 x 2 4 x 1 + x 2 4 x 1 0, x 2 0

• Após introduzir variáveis de folga e aplicar o algoritmo simplex, obtém-se a tabela simplex ótima com x 1=5, x 2=1, x 3=0, x 4=0, x 5=8, e f=-6 x 1 VB 0 x 2 x 3 x 4 x 5 0 1 0 0 f+6 x 2 0 1 0, 5 -0, 5 0 1 x 1 1 0 0, 5 0 5 x 5 0 0 0 1 1 8 • Note que a base ótima pode ser alterada, introduzindo x 4 e retirando x 5 sem que o valor da função objetivo mude, ou seja, obtendo-se uma solução alternativa ótima ( Verifique isso com uma nova iteração)

Note, entretanto, que • se no exemplo anterior, a solução da tabela simplex ótima apresentasse uma variável básica nula, a entrada de x 4 na base poderia provocar a diminuição do valor desta variável básica, tornando-a, portanto, negativa • Como isso não pode ocorrer, x 4 não poderia entrar na base Em outras palavras, O problema não apresentaria soluções ótimas alternativas, mesmo tendo variáveis não básicas com custos relativos iguais a zero na tabela simplex ótima

Exercício: Minimizar f(x 1, x 2) = x 1 x 2 x 1 + x 2 6 x 1 x 2 4 x 2 1 x 1 0, x 2 0

Degenerescência em PLs Uma solução factível é dita degenerada se alguma variável básica for nula Um PL é dito degenerado se existe pelo menos uma solução básica factível degenerada Exemplo: Minimizar f(x 1, x 2) = 5 x 1 2 x 2 x 1 + x 2 6 x 1 x 2 0 x 1 0, x 2 0

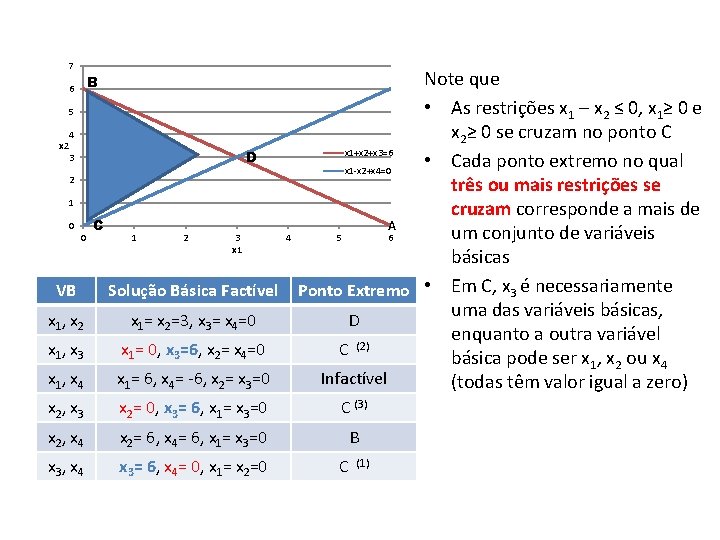
7 5 x 2 Note que • As restrições x 1 – x 2 ≤ 0, x 1≥ 0 e x 2≥ 0 se cruzam no ponto C x 1+x 2+x 3=6 D • Cada ponto extremo no qual x 1 -x 2+x 4=0 três ou mais restrições se cruzam corresponde a mais de A C um conjunto de variáveis 1 2 3 4 5 6 x 1 básicas Solução Básica Factível Ponto Extremo • Em C, x 3 é necessariamente uma das variáveis básicas, x 1= x 2=3, x 3= x 4=0 D enquanto a outra variável (2) x 1= 0, x 3=6, x 2= x 4=0 C básica pode ser x 1, x 2 ou x 4 x 1= 6, x 4= -6, x 2= x 3=0 Infactível (todas têm valor igual a zero) B 6 4 3 2 1 0 0 VB x 1, x 2 x 1, x 3 x 1, x 4 x 2, x 3 x 2= 0, x 3= 6, x 1= x 3=0 C (3) x 2, x 4 x 2= 6, x 4= 6, x 1= x 3=0 B x 3, x 4 x 3= 6, x 4= 0, x 1= x 2=0 C (1)

Dificuldades em PLs Degenerados 1. Considere um PL degenerado para o qual a solução ótima tenha valor igual a 30. Suponha também que a solução inicial tenha valor igual a 20 • Como é possível pivotar sem alterar o valor da solução, a aplicação do simplex poderia gerar uma seqüência de soluções (com valor igual a 20) do tipo: sf 1 sf 2 sf 3 • Ou seja, ocorre ciclagem em um conjunto de soluções factíveis, nunca atingindo a solução ótima 2. Mesmo que não ocorra ciclagem, o simplex pode encontrar um grande número de soluções básicas degeneradas antes de descobrir que não correspondem a soluções ótimas (último exemplo) • Isso significa que o simplex geralmente não é um método eficiente para resolver problemas degenerados

@ Lista 3: Aplique o método Simplex ao seguinte PL 1) Maximizar f(x 1, x 2, x 3, x 4) = 10 x 1 - 57 x 2 - 9 x 3 - 24 x 4 0, 5 x 1 – 5, 5 x 2 – 2, 5 x 3 + 9 x 4 0 0, 5 x 1 – 1, 5 x 2 – 0, 5 x 3 + x 4 0 x 1 1 x 1 ≥ 0, x 2 ≥ 0, x 3 ≥ 0, x 4 ≥ 0

Determinação de Soluções Básicas Factíveis Iniciais Algumas classes de problemas a fornecem naturalmente. Seja: Minimizar f(x) = c. Tx Ax b x≥ 0 Introduzindo as variáveis de folga (xf): Minimizar f(x) = c. Tx Ax + xf= b x, xf ≥ 0 A matriz dos coeficientes das restrições é dada agora por [A I] e B= I as variáveis básicas são as variáveis de folga x. B=xf N=A as variáveis não básicas são as variáveis originais x. N=x e a solução básica factível é: x. B=xf=b x. N=x=0

Entretanto, nem sempre uma solução básica factível está disponível. Por exemplo, Minimizar f(x) = c. Tx Ax = b x≥ 0 Pode-se criar uma base, introduzindo novas variáveis (y): Ax + y = b x ≥ 0, y ≥ 0 As variáveis y são chamadas de variáveis artificiais. Como não fazem parte do problema original devem ser eliminadas Como ?

Opção 1) Um problema artificial, semelhante ao original, é construído: Minimizar fa (x, y) = Ax + y= b x, y ≥ 0 • A função objetivo do problema artificial penaliza as variáveis artificiais. Assim, se houver solução para o problema, a solução deve ter yi=0, i=1, . . . , m. • Se houver variáveis de folga, resultantes de restrições de desigualdade, estas podem ser utilizadas na construção da base inicial, e complementadas por variáveis artificiais

Exercícios: Construa problemas artificiais para: Minimizar f(x 1, . . . , x 3) = x 1 x 2 + 2 x 3 x 1 + x 2 + x 3 = 3 2 x 1 - 2 x 2 + x 3 4 x 1, . . . , x 3 ≥ 0 Variáveis básicas: x. B=[y 1, y 2] Variáveis não básicas: x. N=x e x 4 PA 1: Uma variável artificial é introduzida em cada restrição Minimizar f(y 1, y 2) = y 1 + y 2 x 1 + x 2 + x 3 + y 1 = 3 2 x 1 - 2 x 2 + x 3 + x 4 + y 2 = 4 x 1, . . . , x 4, y 1, y 2 ≥ 0 Forma padrão: Minimizar f(x 1, . . . , x 4) = x 1 x 2 + 2 x 3 + 0 x 4 x 1 + x 2 + x 3 = 3 2 x 1 - 2 x 2 + x 3 + x 4 = 4 x 1, . . . , x 4 ≥ 0 Variáveis básicas: x. B=[x 4, y] Variáveis não básicas: x. N=x PA 2: Uma variável artificial é introduzida somente na 1ª restrição Minimizar f(x 5) = y x 1 + x 2 + x 3 + y = 3 2 x 1 - 2 x 2 + x 3 + x 4 = 4 x 1, . . . , x 4, y ≥ 0

• Ao final da resolução do problema artificial, as variáveis artificiais são não básicas (nulas segundo o objetivo deste problema) e uma base com as colunas originais de A é obtida. • Se o problema original tem solução factível , então • Esta solução é ótima para o problema artificial pois é equivalente a (x, y)= , a qual é factível para aquele problema e minimiza a função objetivo daquele problema • Isso mostra que o problema artificial tem, em geral, infinitas soluções ótimas (qualquer solução factível do problema original)

Uma vez encontrada uma solução básica em que todas as variáveis artificiais são não básicas, o método simplex é aplicado para resolver o problema original a partir desta base Este método é denominado MÉTODO DAS DUAS FASES Fase 1: Resolva o problema artificial (pivoteie de forma a deixar a primeira linha na forma padrão) Se na solução ótima deste problema alguma variável artificial for não nula, o problema original é infactível (fim). Caso contrário: Fase 2: Elimine as colunas das variáveis artificiais. Substitua os coeficientes da primeira linha pelos coeficientes da função objetivo do problema original. Pivoteie de forma a deixar a primeira linha na forma padrão. Resolva o problema original a partir desta tabela.

Exemplo: Max 3 x 1 + x 2 - x 1 + x 2 1 x 1 + x 2 3 2 x 1 + x 2 2 x 1, x 2 0 Forma padrão com variáveis artificiais Min -3 x 1 - x 2 - x 1 + x 2 - x 3 + y 1 = 1 x 1 + x 2 - x 4 + y 2 = 3 2 x 1 + x 2 + x 5 = 2 x 1, x 2 , x 3 , x 4, x 5 , y 1, y 2 0 **Note que x 3 e x 4 (variáveis de excesso) não servem para a base pois teriam valores negativos (x 3=-1 e x 4=-3) em tal solução Aplicação do Método de Duas fases Fase 1 Min y 1 + y 2 - x 1 + x 2 - x 3 + y 1 = 1 x 1 + x 2 - x 4 + y 2 = 3 2 x 1 + x 2 + x 5 = 2 x 1, x 2 , x 3 , x 4, x 5 , y 1, y 2 0 A resolução se encontra no arquivo “Exemplo de duas fases”

• Opção 2) Uma alternativa ao método das duas fases consiste em adicionar à função objetivo original, um termo M (valor muito grande) que penaliza fortemente as variáveis artificiais, e aplicar o simplex, o qual procurará torná-las iguais a 0: Minimizar f(x 1, . . . , x 5) = x 1 x 2 + 2 x 3+ My x 1 + x 2 + x 3 + y = 3 2 x 1 - 2 x 2 + x 3 + x 4 = 4 Este método é denominado MÉTODO DO BIG-M

Relações entre PLs e os Problemas Artificiais Associados PL ARTIFICIAL PL ORIGINAL Alguma variável artificial não nula na tabela ótima Infactível Ilimitado e todas as variáveis artificiais nulas na tabela ótima Ilimitado e alguma variável artificial positiva na tabela ótima Infactível

Uma Alternativa ao Simplex Métodos de Pontos Interiores Gera pontos interiores da região factível buscando a convergência a uma solução ótima