Introduo ao MATLAB Basico www opencadd com br

Introdução ao MATLAB Basico www. opencadd. com. br

Introduction to MATLAB Online Help • • • » The help command >> help The help window >> helpwin The lookfor command >> lookfor CD help cd Change current working directory. CD directory-spec sets the current directory to the one specified. CD. . moves to the directory above the current one. CD, by itself, prints out the current directory. WD = CD returns the current directory as a string. Use the functional form of CD, such as CD('directory-spec'), when the directory specification is stored in a string. See also PWD. Copyright ã 1984 - 1998 by The Math. Works, Inc.

Introduction to MATLAB Calculations at the Command Line MATLAB as a calculator Assigning Variables » » a = 2; -5/(4. 8+5. 32)^2 ans = -0. 0488 » (3+4 i)*(3 -4 i) » b = 5; » a^b ans = 32 ans = 25 » cos(pi/2) ans = » x = 5/2*pi; » y = sin(x) exp(acos(0. 3)) ans = 3. 5470 » cmd_line Results assigned to “ans” if name not specified y = 1 6. 1230 e-017 » Semicolon suppresses screen output » z = asin(y) z = () parentheses for function inputs 1. 5708 Numbers stored in double-precision floating point format Copyright ã 1984 - 1998 by The Math. Works, Inc.

Introduction to MATLAB Working with Files & Variables • • CD / PWD, LS / DIR - navigating directories • • ! - invoke operating system • • CLEAR - remove function / variable from memory • SIZE - returns the size of matrix WHAT - displays the files within a directory (grouped by type) WHICH - identifies the object referenced by given name (function / variable) WHOS - lists workspace variables and details (size, memory usage, data type) Ref: Utility Commands Copyright ã 1984 - 1998 by The Math. Works, Inc.

Introduction to MATLAB Workspace Browser Command line variables saved in MATLAB workspace » workspace Copyright ã 1984 - 1998 by The Math. Works, Inc.

Introduction to MATLAB Array Editor For editing 2 -D numeric arrays double-click / Open » openvar ans Copyright ã 1984 - 1998 by The Math. Works, Inc.

Introduction to MATLAB Working with Matrices MATLAB == MATrix LABoratory » load durer » image(X); » colormap(map) » load detail » image(X); » colormap(map) Copyright ã 1984 - 1998 by The Math. Works, Inc.

Introduction to MATLAB The Matrix in MATLAB Columns (n) 2 3 4 1 A= 6 1 11 6 16 1. 2 7 9 12 4 17 25 22 7. 2 3 5 8 7 13 1 18 11 23 4 0. 5 9 4 14 5 19 56 24 5 23 5 83 10 13 15 0 20 10 25 1 2 Rows (m) 3 4 1 8 2 5 10 Matrix elements can be EITHER numbers OR characters 2 21 A (2, 4) A (17) Rectangular Matrix: Scalar: 1 -by-1 array Vector: m-by-1 array 1 -by-n array Matrix: m-by-n array Copyright ã 1984 - 1998 by The Math. Works, Inc.

Introduction to MATLAB Entering Numeric Arrays Row separator: semicolon (; ) Column separator: space / comma (, ) » a=[1 2; 3 4] Use square brackets [ ] a = 1 2 3 4 » b=[-2. 8, sqrt(-7), (3+5+6)*3/4] b = -2. 8000 Matrices must be rectangular. (Set undefined elements to zero) 0 + 2. 6458 i 10. 5000 » b(2, 5) = 23 b = -2. 8000 0 + 2. 6458 i 10. 5000 0 0 0 23. 0000 Any MATLAB expression can be entered as a matrix element » num_array 1 Copyright ã 1984 - 1998 by The Math. Works, Inc.

Introduction to MATLAB Entering Numeric Arrays - cont. Scalar expansion Creating sequences: colon operator (: ) » w=[1 2; 3 4] + 5 w = 6 7 8 9 » x = 1: 5 x = 1 2 » y = 2: -0. 5: 0 Utility functions for creating matrices. (Ref: Utility Commands) 3 y = 2. 0000 1. 5000 » z = rand(2, 4) 4 5 1. 0000 0. 5000 0. 8913 0. 7621 0. 4565 0. 0185 0 z = 0. 9501 0. 2311 0. 6068 0. 4860 » num_array 2 Copyright ã 1984 - 1998 by The Math. Works, Inc.

Introduction to MATLAB Numerical Array Concatenation - [ ] Use [ ] to combine existing arrays as matrix “elements” Row separator: semicolon (; ) Column separator: space / comma (, ) » a=[1 2; 3 4] Use square brackets [ ] a = 1 2 3 4 » cat_a=[a, 2*a; 3*a, cat_a = 1 2 2 3 4 6 3 6 4 9 12 12 5 10 6 15 20 18 4*a; 5*a, 6*a] 4 8 8 16 12 24 4*a The resulting matrix must be rectangular. » num_cat Copyright ã 1984 - 1998 by The Math. Works, Inc.

Introduction to MATLAB Array Subscripting / Indexing 1 A= A(3, 1) A(3) • • 4 1 2 8 2 3 7. 2 3 4 0 4 5 23 5 1 2 3 4 5 6 1 11 6 16 1. 2 7 9 12 4 17 5 8 7 13 1 18 11 23 0. 5 9 4 14 5 19 56 24 83 10 13 15 0 20 10 25 10 2 21 25 22 A(1: 5, 5) A(1: end, end) A(: , 5) A(: , end) A(21: 25) A(21: end)’ A(4: 5, 2: 3) A([9 14; 10 15]) Use () parentheses to specify index colon operator (: ) specifies range / ALL [ ] to create matrix of index subscripts ‘end’ specifies maximum index value Copyright ã 1984 - 1998 by The Math. Works, Inc.

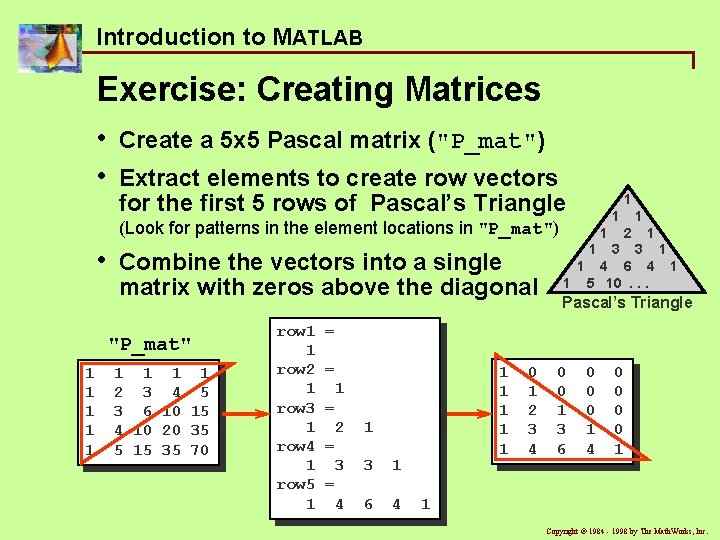
Introduction to MATLAB Exercise: Creating Matrices • • Create a 5 x 5 Pascal matrix ("P_mat") Extract elements to create row vectors for the first 5 rows of Pascal’s Triangle 1 1 (Look for patterns in the element locations in "P_mat") • Combine the vectors into a single matrix with zeros above the diagonal "P_mat" 1 1 1 1 1 2 3 4 5 3 6 10 15 4 10 20 35 5 15 35 70 row 1 1 row 2 1 row 3 1 row 4 1 row 5 1 1 1 2 3 1 3 4 6 4 5 10. . . 1 1 Pascal’s Triangle = = 1 1 1 = 2 1 = 3 3 1 6 4 0 1 2 3 4 0 0 1 3 6 0 0 0 1 4 0 0 1 = 4 1 Copyright ã 1984 - 1998 by The Math. Works, Inc.

Introduction to MATLAB Solution: Creating Matrices (1) » P_mat = pascal(5) % Create Pascal's Matrix » row 1 = P_mat(1) % Extract Rows » row 2 = P_mat(2: 4: 6). . . » row 5 = P_mat(5: 4: 21) » new_mat = row 1 % Create New Matrix » new_mat(2, 1: 2) = row 2. . . » new_mat(5, 1: 5) = row 5 % NOTE: GENERALIZED FORM: % Nmax = length(P_mat); % row. N = P_mat(N: Nmax-1: (N-1)*Nmax+1) % new_mat(N, 1: N) = row. N » create_mat Copyright ã 1984 - 1998 by The Math. Works, Inc.

Introduction to MATLAB Solution: Creating Matrices (2) » P_mat = pascal(5) % Create Pascal's Matrix % Rearrange Matrix - Pascal Triangle in upper triangle % Flip Matrix Horizontally (LEFT-RIGHT): % - Could also use FLIPLR(): » temp = P_mat(1: 5, 5: -1: 1) % Extract diagonals (rows of Pascal’s Triangle) » row 1 = diag(temp, 4)' » row 2 = diag(temp, 3)' » row 3 = diag(temp, 2)' » row 4 = diag(temp, 1)' » row 5 = diag(temp)' % Create New Matrix as before » create_mat Copyright ã 1984 - 1998 by The Math. Works, Inc.

Introduction to MATLAB Solution: Creating Matrices (3) » P_mat = pascal(5) % Create Pascal's Matrix % Rearrange Matrix - Pascal Triangle in lower triangle % Flip Matrix Vertically (UP-DOWN): % - Could also use FLIPUD(): » temp 1 = P_mat(5: -1: 1, 1: 5) % Extract lower triangular matrix: » temp 2 = tril(temp 1) % Create New Matrix by sorting columns of "temp 2": » new_mat = sort(temp 2) » create_mat Copyright ã 1984 - 1998 by The Math. Works, Inc.

Introduction to MATLAB Matrices & Linear Algebra (In order of precedence) » help ops » help matfun Copyright ã 1984 - 1998 by The Math. Works, Inc.

Introduction to MATLAB Matrix Multiplication • • Inner dimensions must be equal • Resulting elements = dot product of the rows of the 1 st matrix with the columns of the 2 nd matrix Dimension of resulting matrix = outermost dimensions of multiplied matrices » a = [1 2 3 4; 5 6 7 8]; [2 x 4] » b = ones(4, 3); [4 x 3] [2 x 3] » c = a*b [2 x 4]*[4 x 3] c = 10 26 a(2 nd row). b(3 rd column) » mat_mult Copyright ã 1984 - 1998 by The Math. Works, Inc.

Introduction to MATLAB Solving Simultaneous Equations using “Left Division” [A]{x} = {b} • {x} = ? If [A] is square matrix (m = n): {x} = [A]-1{b} [A] = mxn {x} = nx 1 {b} = mx 1 » x = inv(A)*b; » x = Ab; Error if singular Warning if nearly singular • For overdetermined system (m>n): using Least squares regression “curve fit” of data » x = Ab; Warning if rank deficient (dependent columns) - solution not unique • For undetermined system (m<n): using QR factorization with column pivoting » x = Ab; Never unique Copyright ã 1984 - 1998 by The Math. Works, Inc.

Introduction to MATLAB Example: Solving Equations • Solve this set of simultaneous equations: » A = [-1 1 2; 3 -1 1; -1 3 4]; » b = [2; 6; 4]; » x = inv(A)*b x = 1. 0000 -1. 0000 2. 0000 » x = Ab -x 1 + x 2 + 2 x 3 = 2 3 x 1 - x 2 + x 3 = 6 -x 1 + 3 x 2 + 4 x 3 = 4 x = 1. 0000 -1. 0000 2. 0000 » solve_examp Copyright ã 1984 - 1998 by The Math. Works, Inc.

Introduction to MATLAB Array Multiplication • • Matrices must have the same dimensions • Resulting elements = product of corresponding elements from the original matrices Dimensions of resulting matrix = dimensions of multiplied matrices » a = [1 2 3 4; 5 6 7 8]; » b = [1: 4; 1: 4]; » c = a. *b c = 1 5 4 12 9 21 16 32 c(2, 4) = a(2, 4)*b(2, 4) Same rules apply for other array operations » array_mult Copyright ã 1984 - 1998 by The Math. Works, Inc.

Introduction to MATLAB Example: Array Operations • In most languages - use loops: » tic; for I = 1: 1000 Density(I) = Mass(I)/(Length(I)*Width(I)*Height(I)); end; toc elapsed_time = 0. 0500 • Use TIC and TOC to measure elapsed time In MATLAB - use Array Operations: » tic; Density = Mass. /(Length. *Width. *Height); toc elapsed_time = 0 Vectorized code is much faster than loops » array_examp Copyright ã 1984 - 1998 by The Math. Works, Inc.

Introduction to MATLAB Boolean Operations » » Mass = [-2 10 Na. N 30 -11 Inf 31]; all_pos = all(Mass>=0) all_pos = 0 » each_pos = Mass>=0 each_pos = 0 » 1 0 1 1 pos_fin = (Mass>=0)&(isfinite(Mass)) pos_fin = 0 1 0 0 1 1 = TRUE 0 = FALSE » bool_ops Copyright ã 1984 - 1998 by The Math. Works, Inc.

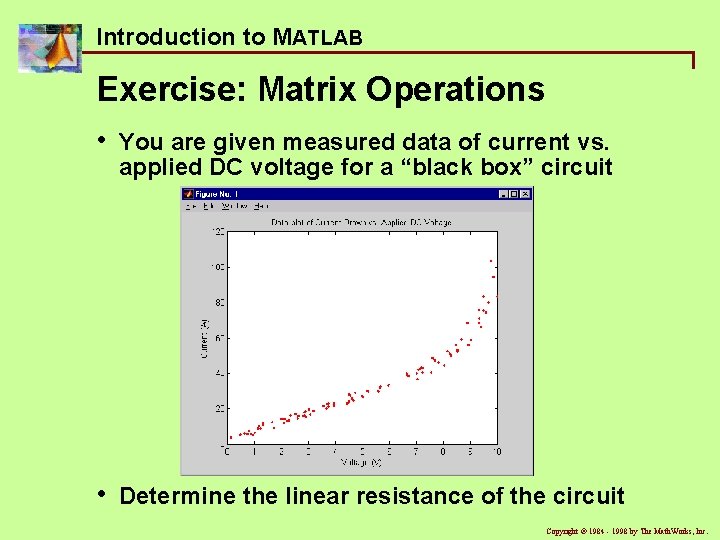
Introduction to MATLAB Exercise: Matrix Operations • You are given measured data of current vs. applied DC voltage for a “black box” circuit • Determine the linear resistance of the circuit Copyright ã 1984 - 1998 by The Math. Works, Inc.

Introduction to MATLAB Solution: Matrix Operations % Assign loaded data: » A = voltage; b = current; % Using left division » x = Ab Initial Fit % Using Pseudoinverse » pseudo_inv_A = inv(A'*A)*A’; Improved fit » x = pseudo_inv_A*b % Repeat using linear data » indices = find(voltage<8); » A = voltage(indices); b = current(indices); . . . » mat_ops (uses: >>mat_ops_setup. m & >>mat_ops. mat) Copyright ã 1984 - 1998 by The Math. Works, Inc.

Introduction to MATLAB String Arrays • Created usingle quote delimiter (') » str = 'Hi there, ' str = Hi there, » str 2 = 'Isn''t MATLAB great? ' str 2 = Isn't MATLAB great? • Each character is a separate matrix element (16 bits of memory per character) str = • H i t h e r e , 1 x 9 vector Indexing same as for numeric arrays » string_array Copyright ã 1984 - 1998 by The Math. Works, Inc.

Introduction to MATLAB String Array Concatenation Using [ ] operator: » str ='Hi there, '; Each row must be same length » str 1='Everyone!'; Row separator: semicolon (; ) new_str = 1 x 19 vectors Hi there, Everyone! » str 2 = 'Isn''t MATLAB great? '; Column separator: space / comma (, ) 1 x 9 vectors » new_str=[str, ' ', str 1] » new_str 2=[new_str; str 2] new_str 2 = Hi there, Everyone! 2 x 19 matrix Isn't MATLAB great? For strings of different length: • STRVCAT • STR 2 MAT » new_str 3 = strvcat(str, str 2) new_str 3 = Hi there, 2 x 19 matrix Isn't MATLAB great? (zero padded) » string_cat Copyright ã 1984 - 1998 by The Math. Works, Inc.

Introduction to MATLAB Working with String Arrays String Comparisons • STRCMP - compare whole strings • STRNCMP - compare first ‘N’ characters • FINDSTR - finds substring within a larger string Converting between numeric & string arrays: • NUM 2 STR - convert from numeric to string array • STR 2 NUM - convert from string to numeric array Copyright ã 1984 - 1998 by The Math. Works, Inc.

Introduction to MATLAB Exercise: String Arrays • • Create a 5 x 5 magic matrix ("M") Use "M" to create a string array which will display as follows: » disp(string_array) 5 x 5 Magic Matrix: New line character 'A' 'B' 'C' 'D' 'E' 1 17 24 1 8 15 2 23 5 7 14 16 3 4 6 13 20 22 4 10 12 19 21 3 5 11 18 25 2 9 HINT: Create rows separately & concatenate Tab character Copyright ã 1984 - 1998 by The Math. Works, Inc.

Introduction to MATLAB Solution: String Arrays » M = magic(5) » M_string = num 2 str(M) » heading = ['5 x 5 Magic Matrix: ', char(10)] » row 0 = [char(9), '''A'' ''B'' ''C'' ''D'' ''E'''] » row 1 = ['1', char(9), M_string(1, : )] » row 2 = ['2', char(9), M_string(2, : )] » row 3 = ['3', char(9), M_string(3, : )] » row 4 = ['4', char(9), M_string(4, : )] » row 5 = ['5', char(9), M_string(5, : )] » string_array = strvcat(heading, row 0, row 1, row 2, row 3, row 4, row 5) » string_soln Copyright ã 1984 - 1998 by The Math. Works, Inc.

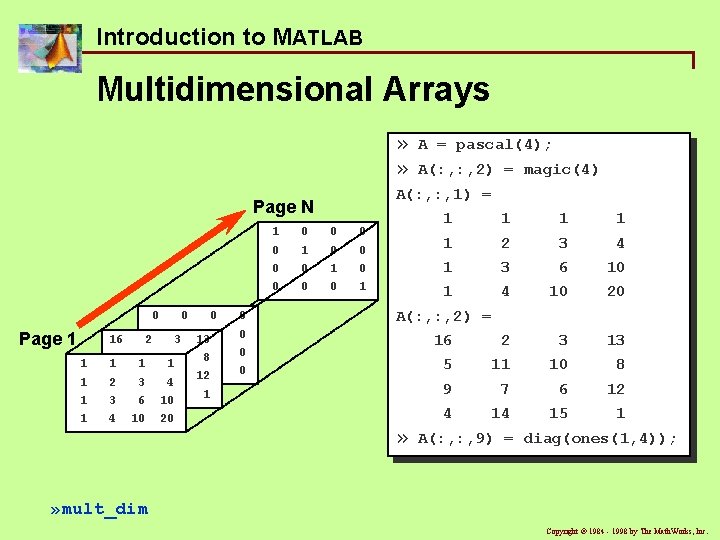
Introduction to MATLAB Multidimensional Arrays » » 5 1 1 1 2 1 3 1 4 9 4 1 1 0 1 2 3 4 1 0 1 3 6 10 0 1 1 4 10 20 1 0 0 0 0 0 A(: , 2) = 20 30 110 100 80 1 1 70 60 120 3 4 14 15 1 6 10 0 16 2 3 13 5 11 10 8 9 7 6 12 4 14 15 1 0 16 A(: , 2) = magic(4) A(: , 1) = Page N Page 1 A = pascal(4); 10 0 20 0 0 » A(: , 9) = diag(ones(1, 4)); » mult_dim Copyright ã 1984 - 1998 by The Math. Works, Inc.