Introductory Statistics Outline for Next Three Subjects Shape

Introductory Statistics

Outline for Next Three Subjects Shape of Quantitative Distributions • Center of Quantitative Distributions • Spread or Variability of Quantitative Distributions •

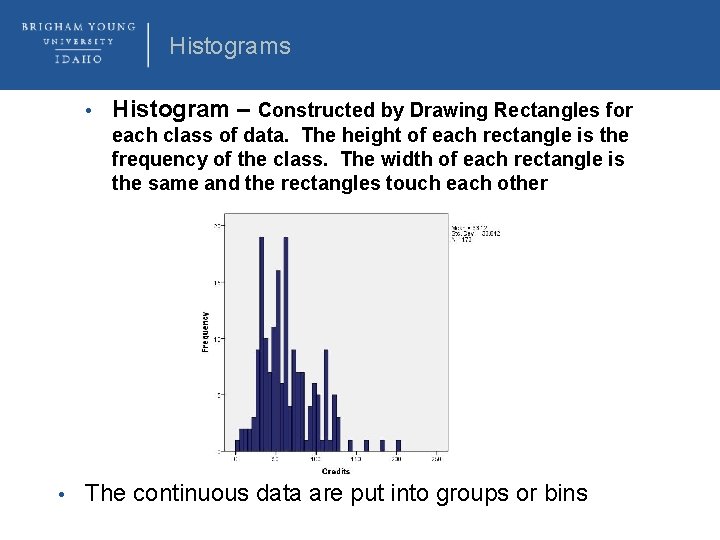
Histograms • Histogram – Constructed by Drawing Rectangles for each class of data. The height of each rectangle is the frequency of the class. The width of each rectangle is the same and the rectangles touch each other • The continuous data are put into groups or bins

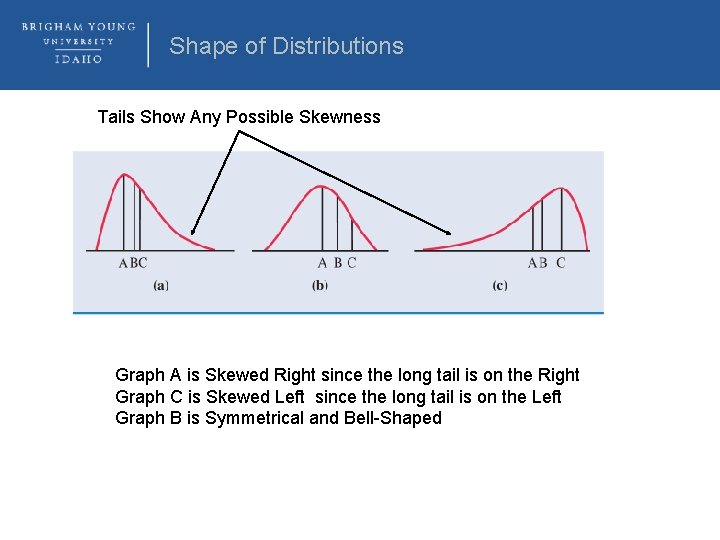
Shape of Distributions Tails Show Any Possible Skewness Graph A is Skewed Right since the long tail is on the Right Graph C is Skewed Left since the long tail is on the Left Graph B is Symmetrical and Bell-Shaped

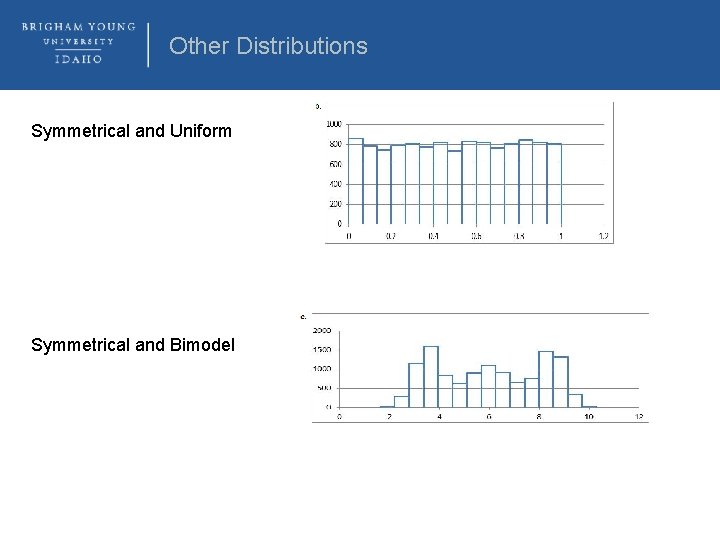
Other Distributions Symmetrical and Uniform Symmetrical and Bimodel

Measures of Center • Mean – Value computed by summing of all of the values of a variable in a data set, divided by the number of observations • Median – Value that lies in the middle of the data set when arranged in ascending order. Half of the data are below the median and half are above the median o Arrange in ascending order o Determine the number of observations, n o If n is odd, then the median is the observation that lies in the (n+1)/2 position (or center position) o If n is even, then the median is the mean of the middle two observations (e. g. , the mean of the two data points that lie on either side of the (n+1)/2 position • Mode – Most frequent observation that occurs (not used as much as mean and median) Example: Children’s ages, Heart Rate

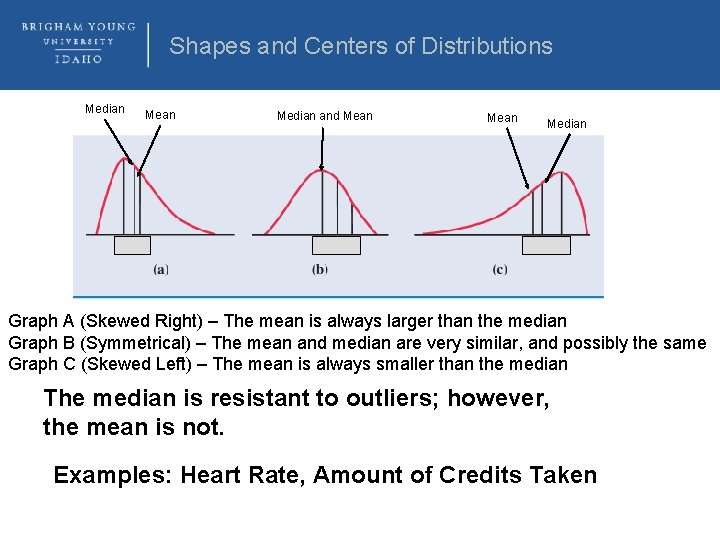
Shapes and Centers of Distributions Median and Mean Median Graph A (Skewed Right) – The mean is always larger than the median Graph B (Symmetrical) – The mean and median are very similar, and possibly the same Graph C (Skewed Left) – The mean is always smaller than the median The median is resistant to outliers; however, the mean is not. Examples: Heart Rate, Amount of Credits Taken