Introductory Physics Last Lecture Angular velocity acceleration Rotational

Introductory Physics

Last Lecture • Angular velocity, acceleration • Rotational/ Linear analogy (angle in radians) • • Centripetal acceleration: (to center)

Newton’s Law of Universal Gravitation • Always attractive • Proportional to both masses • Inversely proportional to separation squared

Gravitation Constant • Determined experimentally • Henry Cavendish, 1798 • Light beam / mirror amplify motion

Weight • Force of gravity on Earth • But we know

Example Often people say astronauts feel weightless, because there is no gravity in space. This explanation is wrong! What is the acceleration due to gravity at the height of the space shuttle (~350 km above the earth surface)? 8. 81 m/s 2 (0. 90 g)

Example (continued) Correct explanation of weightlessness: • Everything (shuttle, people, bathroom scale, etc. ) also falls with same acceleration • No counteracting force (earth’s surface) • “Accelerating Reference Frame” • Same effect would be felt in falling elevator

Example a Astronaut Bob stands atop the highest mountain of planet Earth, which has radius R. Astronaut Ted whizzes around in a circular orbit at Carol the same radius. Astronaut Carol whizzes around in a circular orbit of radius 3 R. Astronaut Alice is simply falling straight downward and is at a radius R, but hasn’t hit the ground yet. Which astronauts experience weightlessness? A. ) All 4 B. ) Ted and Carol C. ) Ted, Carol and Alice Ted Bob Alice

Example b Astronaut Bob stands atop the highest mountain of planet Earth, which has radius R. Astronaut Ted whizzes around in a circular orbit at Carol the same radius. Astronaut Carol whizzes around in a circular orbit of radius 3 R. Astronaut Alice is simply falling straight downward and is at a radius R, but hasn’t hit the ground yet. Assume each astronaut weighs Bob w=180 lbs on Earth. The gravitational force acting on Ted is A. ) w B. ) ZERO Ted Alice

Example c Astronaut Bob stands atop the highest mountain of planet Earth, which has radius R. Astronaut Ted whizzes around in a circular orbit at Carol the same radius. Astronaut Carol whizzes around in a circular orbit of radius 3 R. Astronaut Alice is simply falling straight downward and is at a radius R, but hasn’t hit the ground yet. Assume each astronaut weighs Bob w=180 lbs on Earth. The gravitational force acting on Alice is A. ) w B. ) ZERO Ted Alice

Example d Astronaut Bob stands atop the highest mountain of planet Earth, which has radius R. Astronaut Ted whizzes around in a circular orbit at the same radius. Carol Astronaut Carol whizzes around in a circular orbit of radius 3 R. Astronaut Alice is simply falling straight downward and is at a radius R, but hasn’t hit the ground yet. Assume each astronaut weighs w=180 lbs on Earth. Bob The gravitational force acting on Carol is A. ) w B. ) w/3 Ted C. ) w/9 D. ) ZERO Alice

Example e Astronaut Bob stands atop the highest mountain of planet Earth, which has radius R. Astronaut Ted whizzes around in a circular orbit at the same radius. Carol Astronaut Carol whizzes around in a circular orbit of radius 3 R. Astronaut Alice is simply falling straight downward and is at a radius R, but hasn’t hit the ground yet. Which astronaut(s) undergo an acceleration g=9. 8 m/s 2? A. ) B. ) C. ) D. ) E. ) Alice Bob and Alice and Ted Bob, Ted and Alice Ted All four Bob Alice

Kepler’s Laws • Tycho Brahe (1546 -1601) • Extremely accurate astronomical observations • Johannes Kepler (1571 -1630) • Worked for Brahe • Used Brahe’s data to find mathematical description of planetary motion • Isaac Newton (1642 -1727) • Used his laws of motion and gravitation to derive Kepler’s laws

Kepler’s Laws 1) Planets move in elliptical orbits with Sun at one of the focal points. 2) Line drawn from Sun to planet sweeps out equal areas in equal times. 3) The square of the orbital period of any planet is proportional to cube of the average distance from the Sun to the planet.

Kepler’s First Law • Planets move in elliptical orbits with the Sun at one focus. • Any object bound to another by an inverse square law will move in an elliptical path • Second focus is empty

Kepler’s Second Law • Line drawn from Sun to planet will sweep out equal areas in equal times • Area from A to B equals Area from C to D. True for any central force due to angular momentum conservation (next chapter)

Kepler’s Third Law • The square of the orbital period of any planet is proportional to cube of the average distance from the Sun to the planet. • The constant depends on Sun’s mass, but is independent of the mass of the planet

Derivation of Kepler’s Third Law m M

Example Data: Radius of Earth’s orbit = 1. 0 A. U. Period of Jupiter’s orbit = 11. 9 years Period of Earth’s orbit = 1. 0 years Find: Radius of Jupiter’s orbit 5. 2 A. U.

Example Given: The mass of Jupiter is 1. 73 x 1027 kg and Period of Io’s orbit is 17 days Find: Radius of Io’s orbit r = 1. 85 x 109 m

Gravitational Potential Energy • PE = mgh valid only near Earth’s surface • For arbitrary altitude • Zero reference level is at r=

Example You wish to hurl a projectile from the surface of the Earth (Re= 6. 38 x 106 m) to an altitude of 20 x 106 m above the surface of the Earth. Ignore rotation of the Earth and air resistance. a) What initial velocity is required? a) 9, 736 m/s b) What velocity would be required in order for the projectile to reach infinitely high? I. e. , what is the escape velocity? b) 11, 181 m/s c) (skip) How does the escape velocity compare to the velocity required for a low earth orbit? c) 7, 906 m/s

Torque • Torque, t , is tendency of a force to rotate object about some axis • F is the force • d is the lever arm (or moment arm) • Units are Newton-meters Door Demo

Torque is vector quantity • Direction determined by axis of twist • Perpendicular to both r and F • Clockwise torques point into paper. Defined as negative • Counter-clockwise torques point out of paper. Defined as positive r - r F + F

Non-perpendicular forces Φ is the angle between F and r

Torque and Equilibrium • Forces sum to zero (no linear motion) • Torques sum to zero (no rotation)

Axis of Rotation • Torques require point of reference • Point can be anywhere • Use same point for all torques • Pick the point to make problem least difficult (eliminate unwanted Forces from equation)

Example 8. 1 Given M = 120 kg. Neglect the mass of the beam. a) Find the tension in the cable b) What is the force between the beam and the wall a) T=824 N b) f=353 N

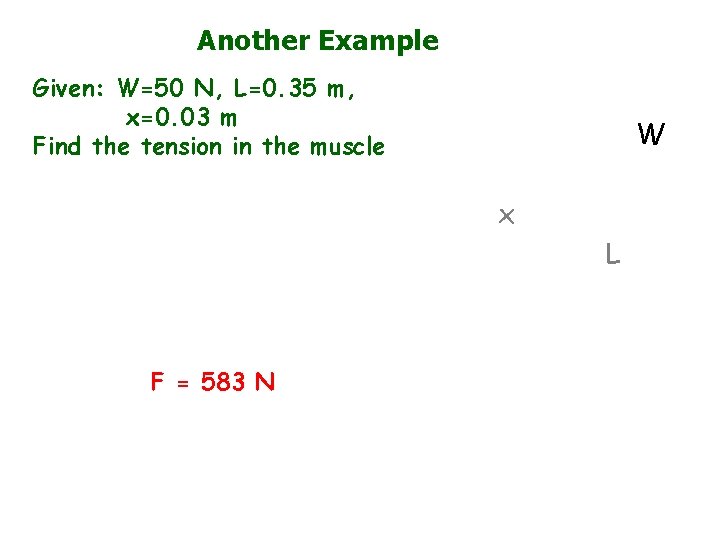
Another Example Given: W=50 N, L=0. 35 m, x=0. 03 m Find the tension in the muscle W x L F = 583 N