Introductory Control Theory I 400B 659 Intelligent robotics

Introductory Control Theory I 400/B 659: Intelligent robotics Kris Hauser

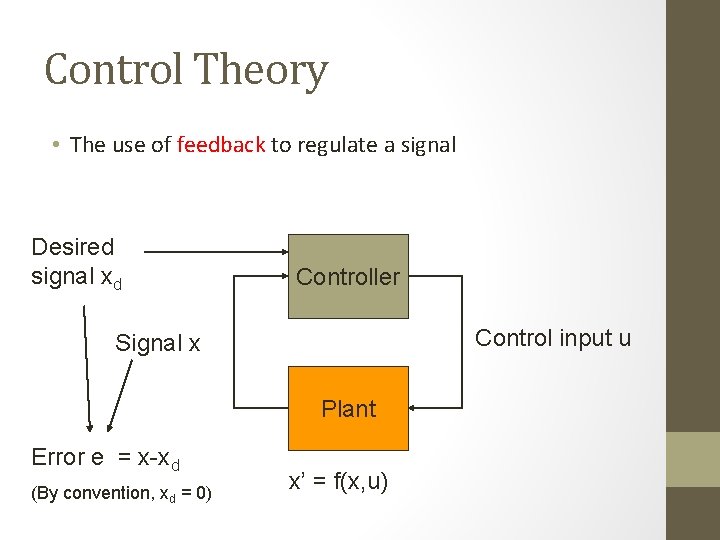
Control Theory • The use of feedback to regulate a signal Desired signal xd Controller Control input u Signal x Plant Error e = x-xd (By convention, xd = 0) x’ = f(x, u)

What might we be interested in? • Controls engineering • Produce a policy u(x, t), given a description of the plant, that achieves good performance • Verifying theoretical properties • Convergence, stability, optimality of a given policy u(x, t)

Agenda • PID control • Feedforward + feedback control • Control is a huge topic, and we won’t dive into much detail

Model-free vs model-based • Two general philosophies: • Model-free: do not require a dynamics model to be provided • Model-based: do use a dynamics model during computation • Model-free methods: • Simpler • Tend to require much more manual tuning to perform well • Model-based methods: • Can achieve good performance (optimal w. r. t. some cost function) • Are more complicated to implement • Require reasonably good models (system-specific knowledge) • Calibration: build a model using measurements before behaving • Adaptive control: “learn” parameters of the model online from sensors

PID control • Proportional-Integral-Derivative controller • A workhorse of 1 D control systems • Model-free

Proportional term Gain • u(t) = -Kp x(t) • Negative sign assumes control acts in the same direction as x x t

Integral term Integral gain • x t Residual steady-state errors driven asymptotically to 0

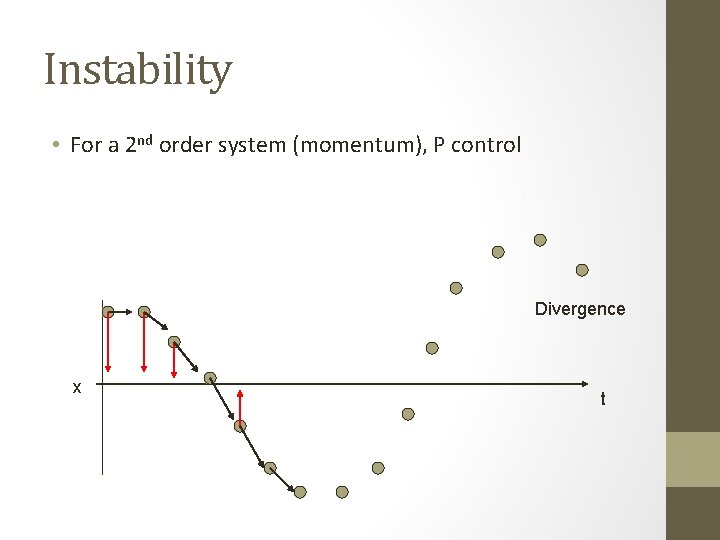
Instability • For a 2 nd order system (momentum), P control Divergence x t

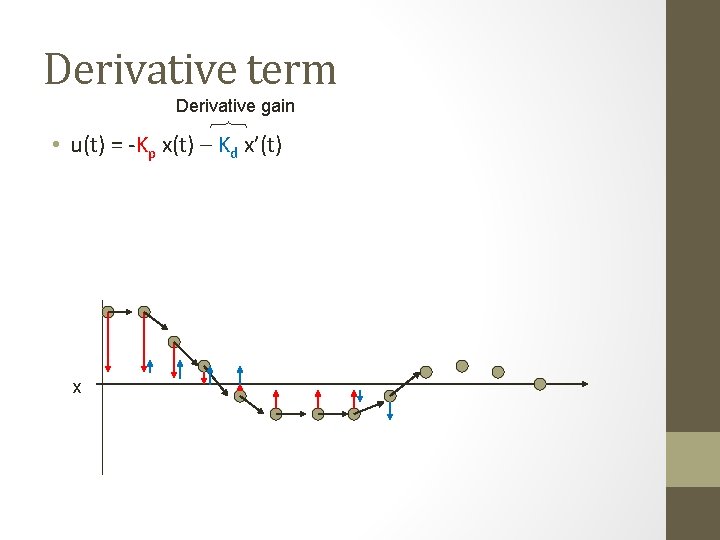
Derivative term Derivative gain • u(t) = -Kp x(t) – Kd x’(t) x

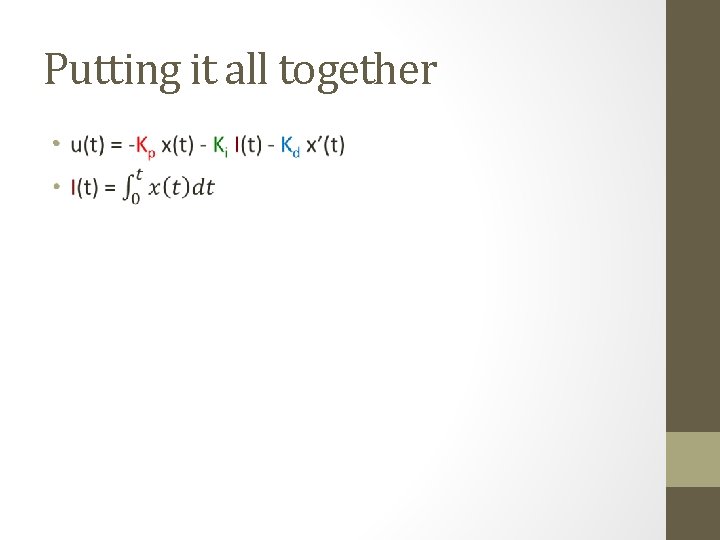
Putting it all together •

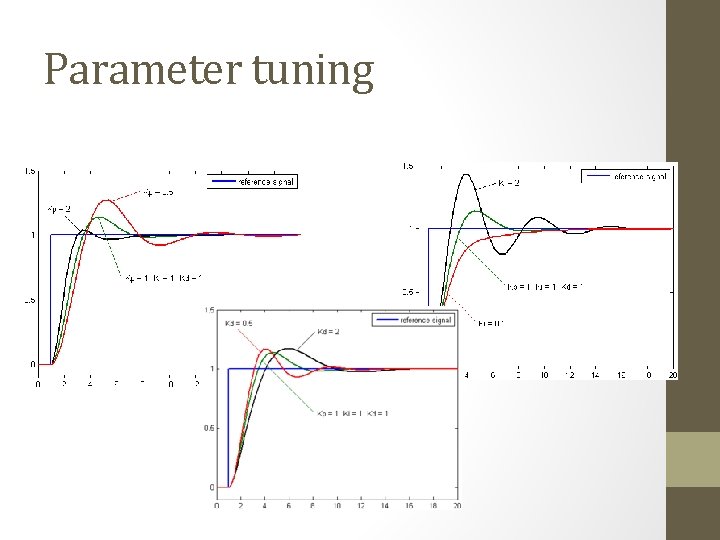
Parameter tuning

Example: Damped Harmonic Oscillator • Second order time invariant linear system, PID controller • x’’(t) = A x(t) + B x’(t) + C + D u(x, x’, t) • For what starting conditions, gains is this stable and convergent?

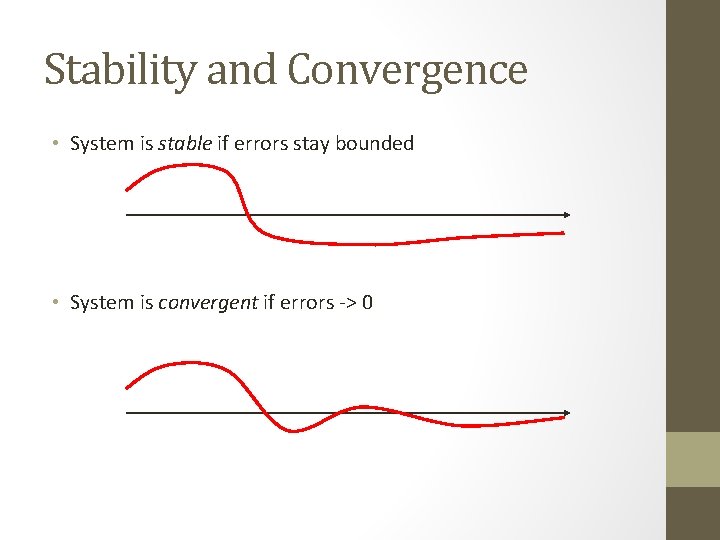
Stability and Convergence • System is stable if errors stay bounded • System is convergent if errors -> 0

Example: Damped Harmonic Oscillator • • x’’ = A x + B x’ + C + D u(x, x’) PID controller u = -Kp x –Kd x’ – Ki I x’’ = (A-DKp) x + (B-DKd) x’ + C - D Ki I Assume Ki=0…

Homogenous solution • • • Instable if A-DKp > 0 Natural frequency w 0 = sqrt(DKp-A) Damping ratio z=(DKd-B)/2 w 0 If z > 1, overdamped If z < 1, underdamped (oscillates)

Example: Trajectory following • x(t) xdes(t) x(t)

Controller Tuning Workflow • Hypothesize a control policy • Analysis: • Assume a model • Assume disturbances to be handled • Test performance either through mathematical analysis, or through simulation • Go back and redesign control policy • Mathematical techniques give you more insight to improve redesign, but require more work

Example

Feedforward control • If we know a model for a system and know how it should move, why don’t we just compute the correct control? • Ex: damped harmonic oscillator • • x’’ = A x + B x’ + C + D u Calculate a trajectory x(t) leading to x(T)=0 at some point T Compute its 1 st and 2 nd derivatives x’(t), x’’(t) Solve for u(t) = 1/D*(x’’(t) - A x(t) + B x’(t) + C) • Would be perfect!

Feedforward control • If we know a model for a system and know how it should move, why don’t we just compute the correct control? • Ex: damped harmonic oscillator • • x’’ = A x + B x’ + C + D u Calculate a trajectory x(t) leading to x(T)=0 at some point T Compute its 1 st and 2 nd derivatives x’(t), x’’(t) Solve for u(t) = 1/D*(x’’(t) - A x(t) + B x’(t) + C) • Problems • Control limits: trajectory must be planned with knowledge of control constraints • Disturbances and modeling errors: open loop control leads to errors not converging to 0

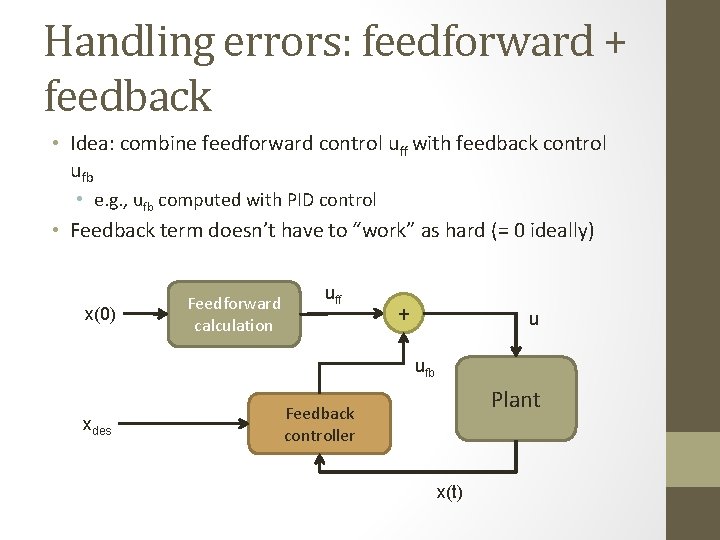
Handling errors: feedforward + feedback • Idea: combine feedforward control uff with feedback control ufb • e. g. , ufb computed with PID control • Feedback term doesn’t have to “work” as hard (= 0 ideally) x(0) Feedforward calculation uff + u ufb xdes Plant Feedback controller x(t)

Application: Feedforward control • Feedback control: let torques be a function of the current error between actual and desired configuration • Problem: heavy arms require strong torques, requiring a stiff system • Stiff systems become unstable relatively quickly

Application: Feedforward control • Solution: include feedforward torques to reduce reliance on feedback • Estimate the torques that would compensate for gravity and achieve desired accelerations (inverse dynamics), send those torques to the motors

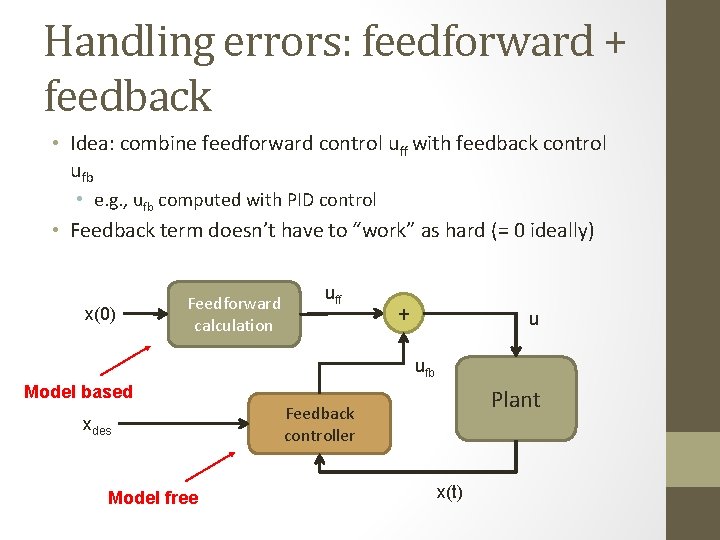
Handling errors: feedforward + feedback • Idea: combine feedforward control uff with feedback control ufb • e. g. , ufb computed with PID control • Feedback term doesn’t have to “work” as hard (= 0 ideally) x(0) Feedforward calculation uff + u ufb Model based xdes Model free Plant Feedback controller x(t)

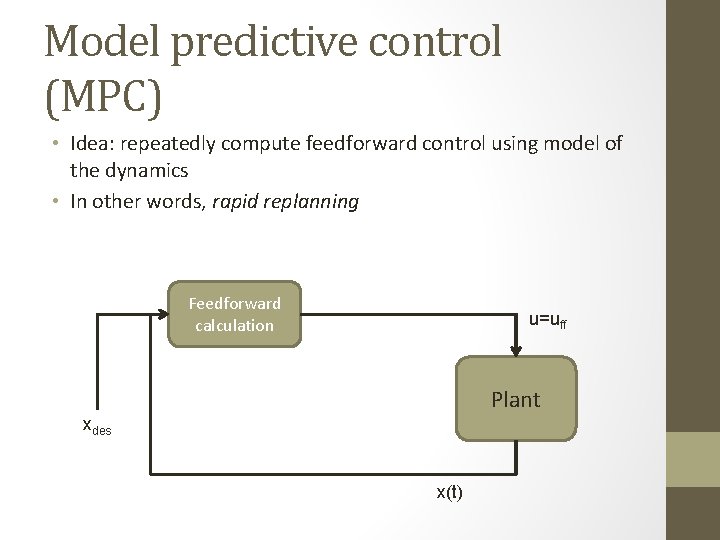
Model predictive control (MPC) • Idea: repeatedly compute feedforward control using model of the dynamics • In other words, rapid replanning Feedforward calculation u=uff Plant xdes x(t)

MPC to avoid moving obstacles

Next class: Sphero Lab • You will design a feedback controller for the “move” command