Introductory Control Theory CS 659 Kris Hauser Control








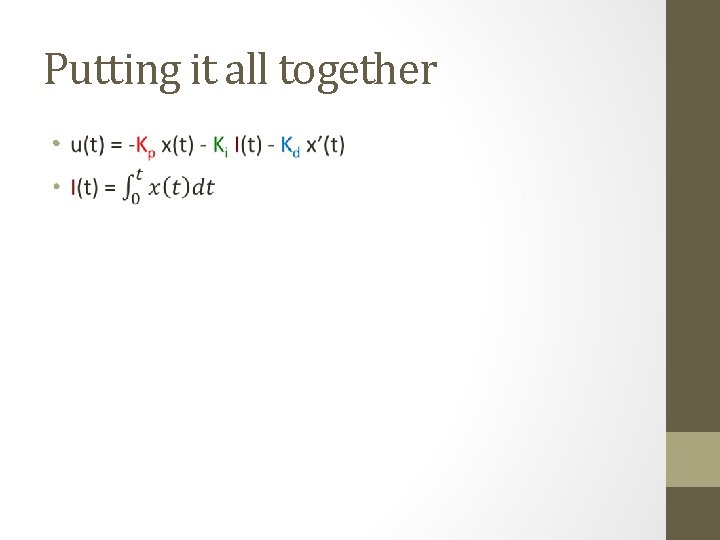

















- Slides: 36

Introductory Control Theory CS 659 Kris Hauser


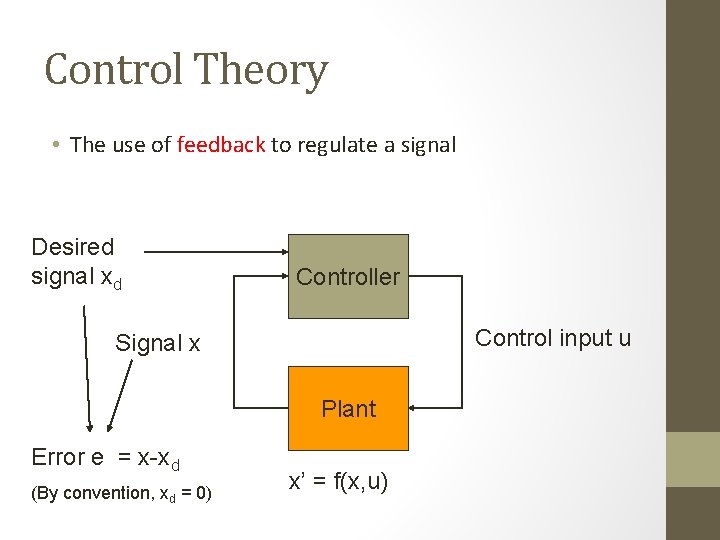
Control Theory • The use of feedback to regulate a signal Desired signal xd Controller Control input u Signal x Plant Error e = x-xd (By convention, xd = 0) x’ = f(x, u)

What might we be interested in? • Controls engineering • Produce a policy u(x, t), given a description of the plant, that achieves good performance • Verifying theoretical properties • Convergence, stability, optimality of a given policy u(x, t)

Agenda • PID control • LTI multivariate systems & LQR control • Nonlinear control & Lyapunov funcitons • Control is a huge topic, and we won’t dive into much detail

Model-free vs model-based • Two general philosophies: • Model-free: do not require a dynamics model to be provided • Model-based: do use a dynamics model during computation • Model-free methods: • Simpler • Tend to require much more manual tuning to perform well • Model-based methods: • Can achieve good performance (optimal w. r. t. some cost function) • Are more complicated to implement • Require reasonably good models (system-specific knowledge) • Calibration: build a model using measurements before behaving • Adaptive control: “learn” parameters of the model online from sensors

PID control • Proportional-Integral-Derivative controller • A workhorse of 1 D control systems • Model-free

Proportional term Gain • u(t) = -Kp x(t) • Negative sign assumes control acts in the same direction as x x t

Integral term Integral gain • x t Residual steady-state errors driven asymptotically to 0

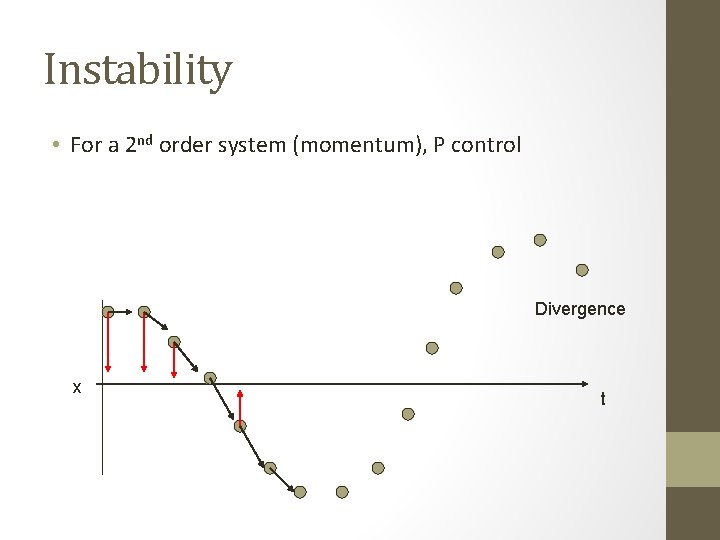
Instability • For a 2 nd order system (momentum), P control Divergence x t

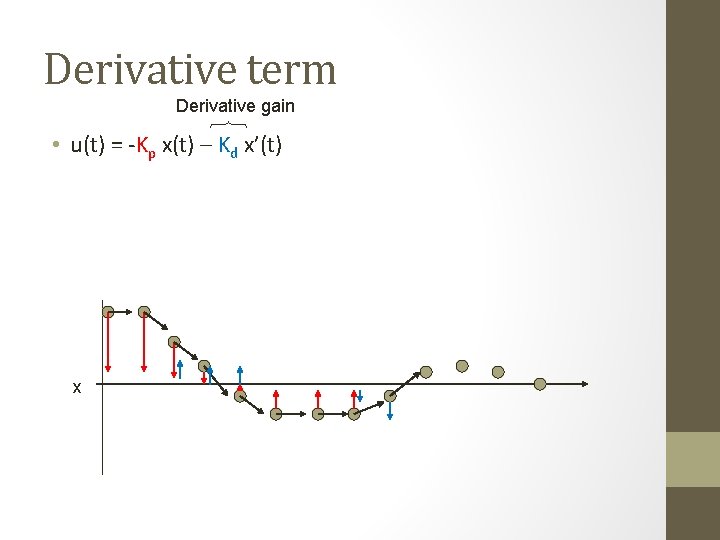
Derivative term Derivative gain • u(t) = -Kp x(t) – Kd x’(t) x
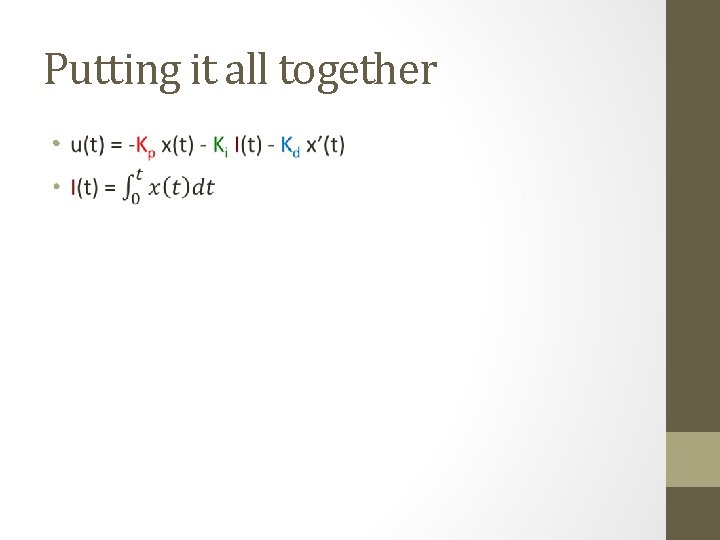
Putting it all together •

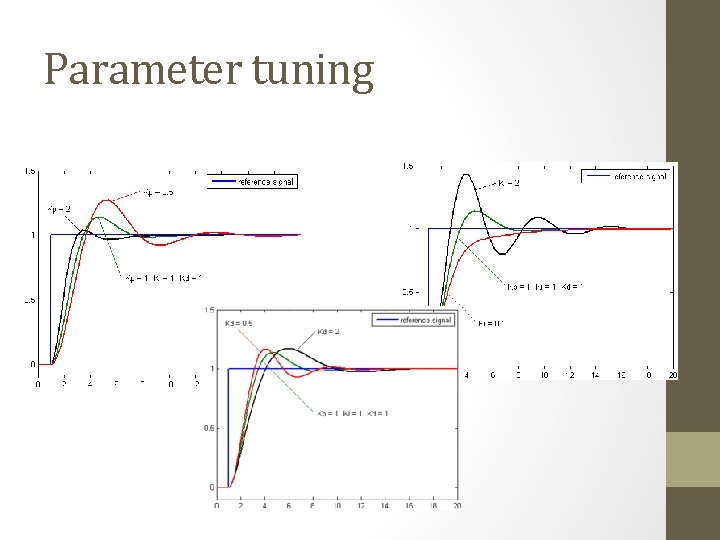
Parameter tuning

Example: Damped Harmonic Oscillator • Second order time invariant linear system, PID controller • x’’(t) = A x(t) + B x’(t) + C + D u(x, x’, t) • For what starting conditions, gains is this stable and convergent?

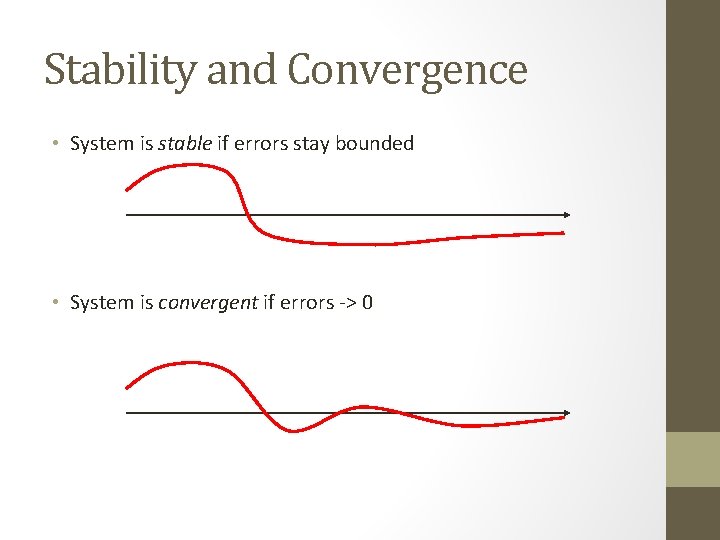
Stability and Convergence • System is stable if errors stay bounded • System is convergent if errors -> 0

Example: Damped Harmonic Oscillator • x’’ = A x + B x’ + C + D u(x, x’) • PID controller u = -Kp x –Kd x’ – Ki I • x’’ = (A-DKp) x + (B-DKd) x’ + C - D Ki I

Homogenous solution • • • Instable if A-DKp > 0 Natural frequency w 0 = sqrt(DKp-A) Damping ratio z=(DKd-B)/2 w 0 If z > 1, overdamped If z < 1, underdamped (oscillates)

Example: Trajectory following • x(t) xdes(t) x(t)

Controller Tuning Workflow • Hypothesize a control policy • Analysis: • Assume a model • Assume disturbances to be handled • Test performance either through mathematical analysis, or through simulation • Go back and redesign control policy • Mathematical techniques give you more insight to improve redesign, but require more work

Multivariate Systems • • x’ = f(x, u) x X Rn u U Rm Because m n, and variables are coupled, this is not as easy as setting n PID controllers

Linear Time-Invariant Systems • Linear: x’ = f(x, u, t) = A(t)x + B(t)u • LTI: x’ = f(x, u) = Ax + Bu • Nonlinear systems can sometimes be approximated by linearization

Convergence of LTI systems • x’ = A x + B u • Let u = - K x • Then x’ = (A-BK) x • The eigenvalues li of (A-BK) determine convergence • Each li may be complex • Must have real component between (-∞, 0]

Linear Quadratic Regulator • x’ = Ax + Bu • Objective: minimize quadratic cost x. TQ x + u. TR u dt Error term “Effort” penalization Over an infinite horizon

Closed form LQR solution • Closed form solution u = -K x, with K = R-1 BP • Where P is a symmetric matrix that solves the Riccati equation • ATP + PA – PBR-1 BTP + Q = 0 • Derivation: calculus of variations • Packages available for finding solution

Nonlinear Control • General case: x’ = f(x, u) • Two questions: • Analysis: How to prove convergence and stability for a given u(x)? • Synthesis: How to find u(t) to optimize some cost function?

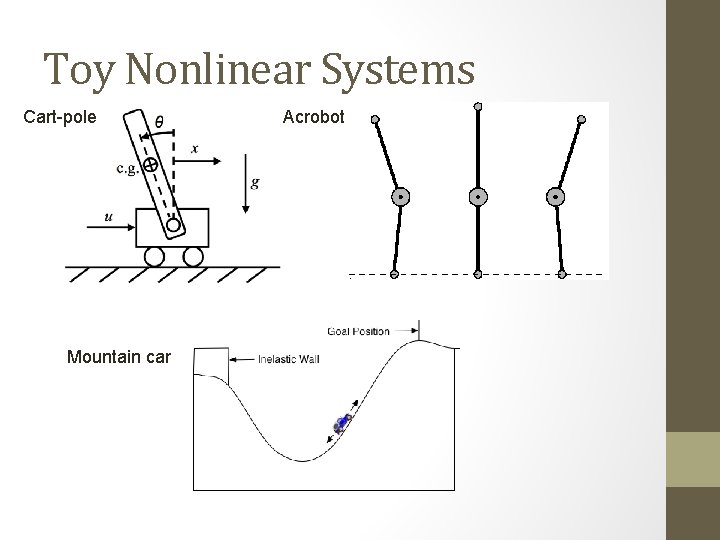
Toy Nonlinear Systems Cart-pole Mountain car Acrobot

Proving convergence & stability with Lyapunov functions • Let u = u(x) • Then x’ = f(x, u) = g(x) • Conjecture a Lyapunov function V(x) • V(x) = 0 at origin x=0 • V(x) > 0 for all x in a neighborhood of origin V(x)

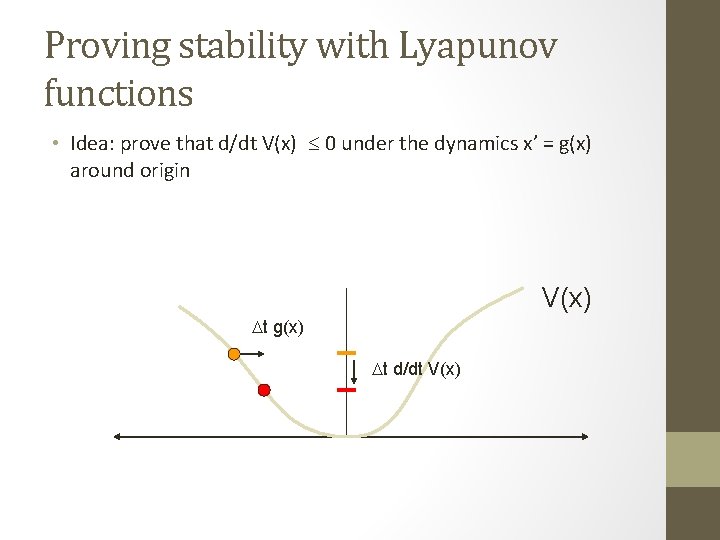
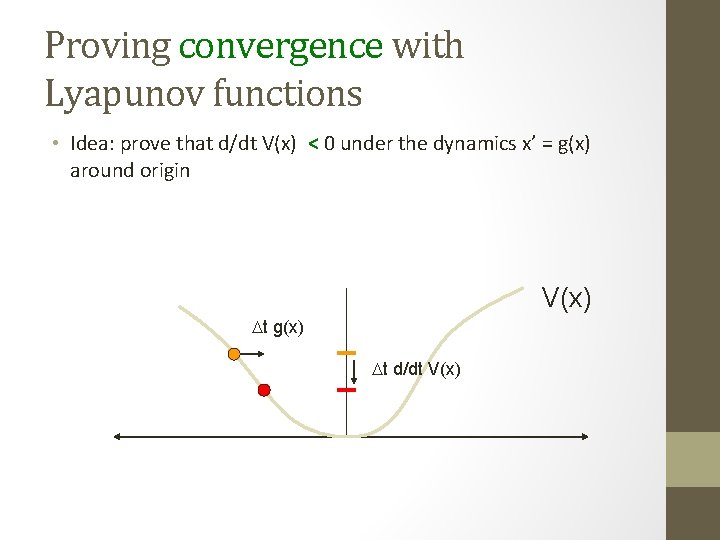
Proving stability with Lyapunov functions • Idea: prove that d/dt V(x) 0 under the dynamics x’ = g(x) around origin V(x) t g(x) t d/dt V(x)

Proving convergence with Lyapunov functions • Idea: prove that d/dt V(x) < 0 under the dynamics x’ = g(x) around origin V(x) t g(x) t d/dt V(x)

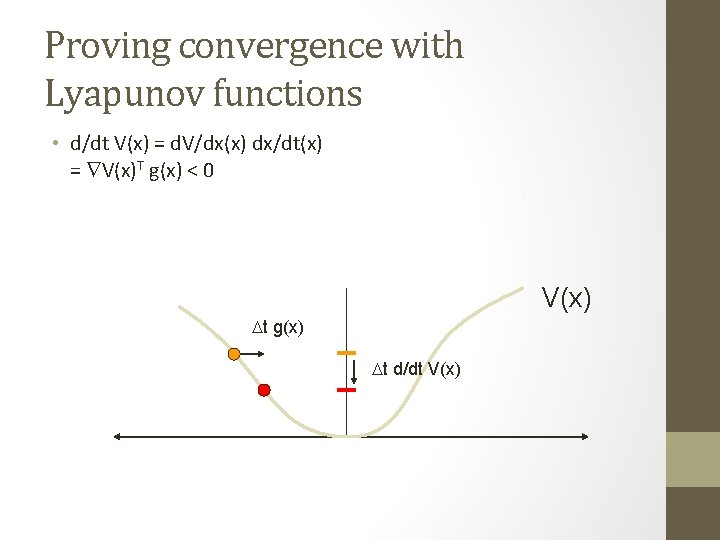
Proving convergence with Lyapunov functions • d/dt V(x) = d. V/dx(x) dx/dt(x) = V(x)T g(x) < 0 V(x) t g(x) t d/dt V(x)

How does one construct a suitable Lyapunov function? • Typically some form of energy (e. g. , KE + PE) • Some art involved

Direct policy synthesis: Optimal control • Input: cost function J(x), estimated dynamics f(x, u), finite state/control spaces X, U • Two basic classes: • Trajectory optimization: Hypothesize control sequence u(t), simulate to get x(t), perform optimization to improve u(t), repeat. • Output: optimal trajectory u(t) (in practice, only a locally optimal solution is found) • Dynamic programming: Discretize state and control spaces, form a discrete search problem, and solve it. • Output: Optimal policy u(x) across all of X

Discrete Search example Split X, U into cells x 1, …, xn, u 1, …, um Build transition function xj = f(xi, uk)dt for all i, k State machine with costs dt J(xi) for staying in state I Find u(xi) that minimizes sum Value function for 1 -joint acrobot of total costs. • Value iteration: repeated dynamic programming over V(xi) = sum of total future costs • •

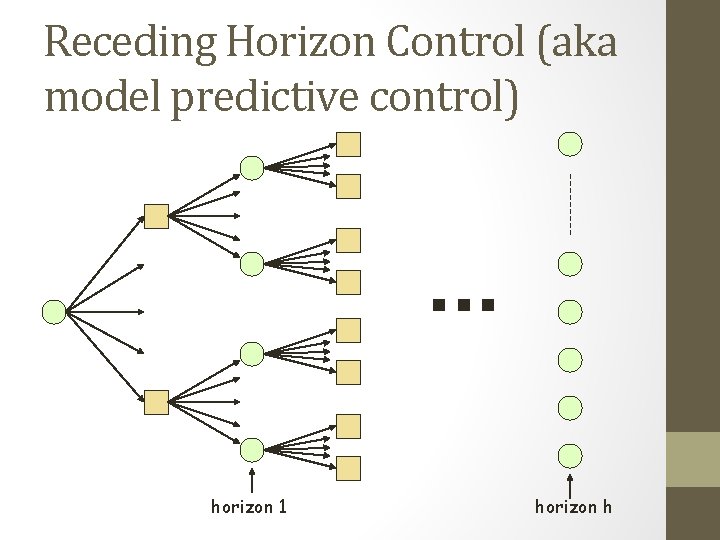
Receding Horizon Control (aka model predictive control) . . . horizon 1 horizon h

Controller Hooks in Robot. Sim • • Given a loaded World. Model sim = Simulator(world) c = sim. get. Controller(0) By default, a trajectory queue, PID controller • c. set. Milestone(qdes) – moves smoothly to qdes • c. add. Milestone(q 1), c. add. Milestone(q 2), … – appends a list of milestones and smoothly interpolates between them. • Can override behavior to get a manual control loop. At every time step, do: • Read q, dq with c. get. Sensed. Config(), c. get. Sensed. Velocity() • For torque commands: • Compute u(q, dq, t) • Send torque command via c. set. Torque(u) • OR for PID commands: • Compute qdes(q, dq, t), dqdes(q, dq, t) • Send PID command via c. set. PIDCommand(qdes, dqdes)

Next class • Motion planning • Principles Ch 2, 5. 1, 6. 1