Introduction week 7 Hi all First of all

Introduction- week 7 Hi all First of all I hope you are all still keeping safe, healthy and looking after yourselves. Now to the boring bit…. Work… My expectation…. I will be expecting you to be doing 5 hours of maths a week. This is no more than what you do in school so it should be relatively straight forward. Now this can be completed by doing an hour a day or spending a few hours on 2 or 3 days completing the entirety of the work, the choice is yours, however, I will be expecting the work to be completed. There will be 4 lessons of NEW CONTENT a week with the 5 th lesson having to complete questions on everything you’ve just learnt (Each lesson 1 hr long). There will be an instruction of how I expect these questions to be completed when you go to lesson 5. I will be providing you with lessons to go through and will be expecting each of you to take notes and answer any questions which are within the slides to help develop your understanding. The week will be topic based so lesson 1 will help with lesson 2 and 3 and so on, so PLEASE DO NOT skip slides. All the lessons will provide you with material on topics that we were yet to cover during your first year at LEEP. If you feel you get stuck or are confused please do not hesitate to contact me. I will be allocating every Wednesday for you to contact with any questions or concerns and will respond to them as soon as I can on the day. However if you have any questions outside of that day I will get back to you as soon as I possibly can. Email: s. rivera@leep. org. uk Please continue to look after yourselves and work hard to ensure we are not having to play catch up when we are back. Mr Rivera

Timetable: Monday – Lesson 1 material Tuesday – Lesson 2 material Wednesday – Lesson 3 material Thursday – Lesson 4 material Friday – Exam questions

Please look at these slides in full screen so you get all the content material. There a lot of slides but please take your time reading through them. Some slides are just additional bits of information for the previous slides so do not be daunted. Remember, if you have any questions you will be able to send an email to me. I will respond as soon as possible. Email: s. rivera@leep. org. uk

Lesson 1

Simultaneous Equations Lesson objective: To be able to solve Simultaneous equations By eliminating method Starter (MWB’s) 3 x – 5 = 4 x=3 2 x + 2 = 30 x = 14 2 x + 3 = 35 x = 16 4 x = 36 x=9 x + 8 = 12 x=4 3 x – 4 = 56 x = 20

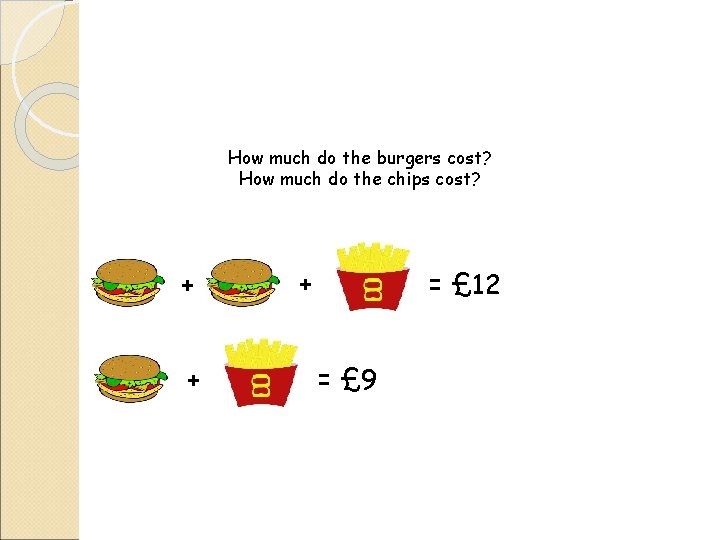
How much do the burgers cost? How much do the chips cost? + + + = £ 12 = £ 9

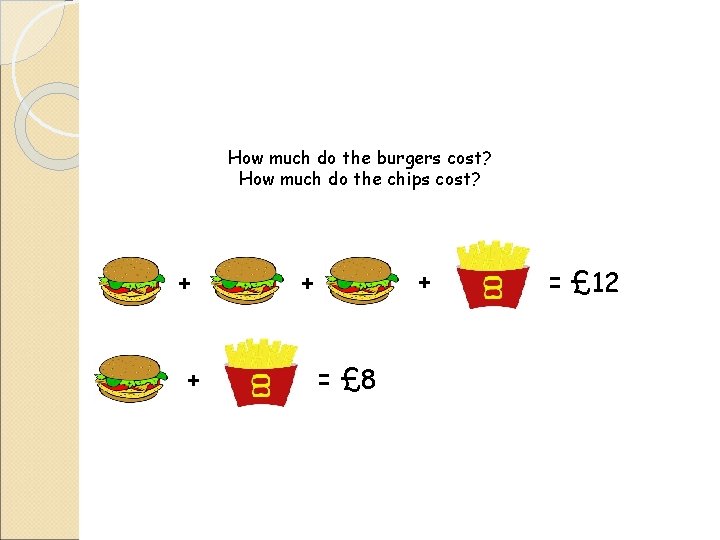
How much do the burgers cost? How much do the chips cost? + + = £ 8 = £ 12

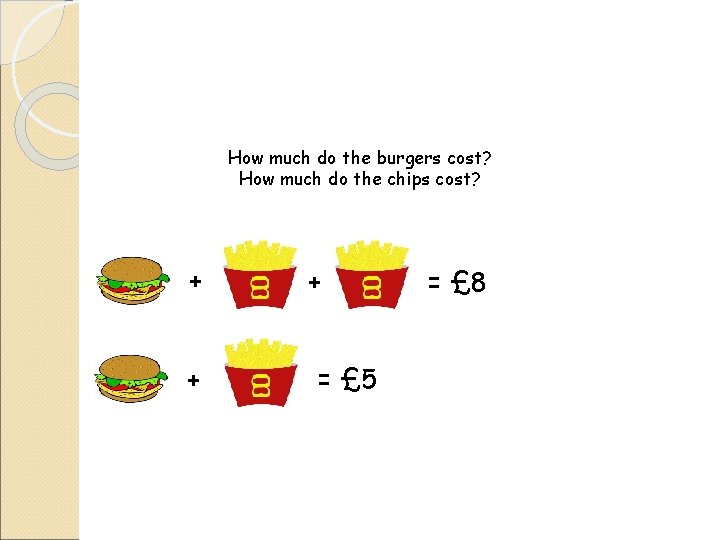
How much do the burgers cost? How much do the chips cost? + + + = £ 5 = £ 8

Simultaneous Equations Simultaneous equations are where two or more equations have two identical unknowns They can be solved algebraically, graphically or by substitution.

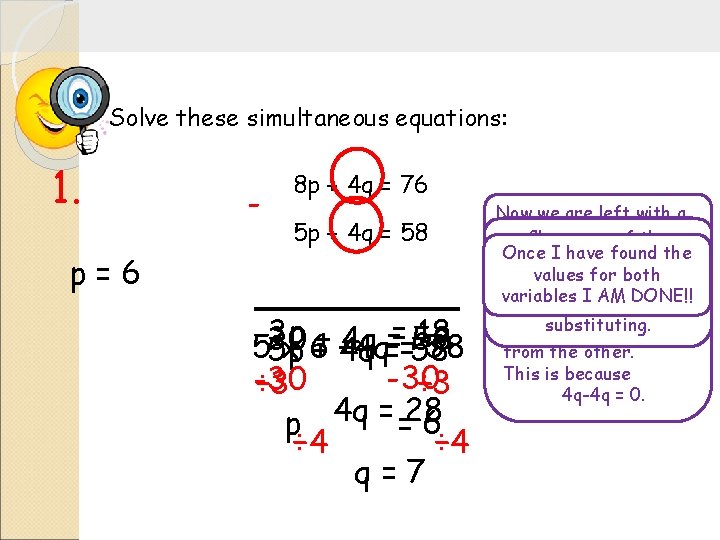
Solve these simultaneous equations: 1. p=6 - 8 p + 4 q = 76 5 p + 4 q = 58 3 p = 18 30 + 4 q = 58 55 p x 6+ 4 q +4 q==58 58 -30 ÷ 3 p 4 q = =28 6 ÷ 4 q=7 Now we are left with a We We want to to eliminate simple linear equation one of theforto So. Chose we have solved one of variables. one of the variables. Once I have found the solve. original equations to one unknowns, Nowof. I our have another values for both substitute now we can Look for anything linear equation tothis solve. To cancel outcalculate ininto. variables I AM DONE!! other common both case the we to have toby substituting. equations. subtract one equation from the other. This is because 4 q-4 q = 0.

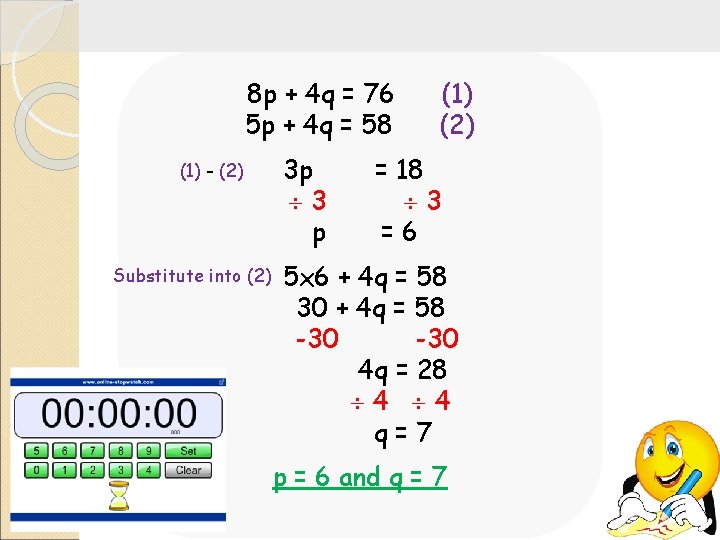
8 p + 4 q = 76 5 p + 4 q = 58 (1) - (2) Substitute into (2) 3 p 3 p (1) (2) = 18 3 =6 5 x 6 + 4 q = 58 30 + 4 q = 58 -30 4 q = 28 4 4 q=7 p = 6 and q = 7

Solve these simultaneous equations: 2. This time it’s the first term in each equation that is common to both. However because the signs are different we add the equations together. -2 a + 5 b = 35 (1) 2 a + 9 b = 35 (2) (1) + (2) Substitute into (2) 14 b = 70 14 b = 5 2 a + 9 x 5 = 35 2 a + 45 = 35 -45 2 a = -10 2 2 a = -5 and b = 5

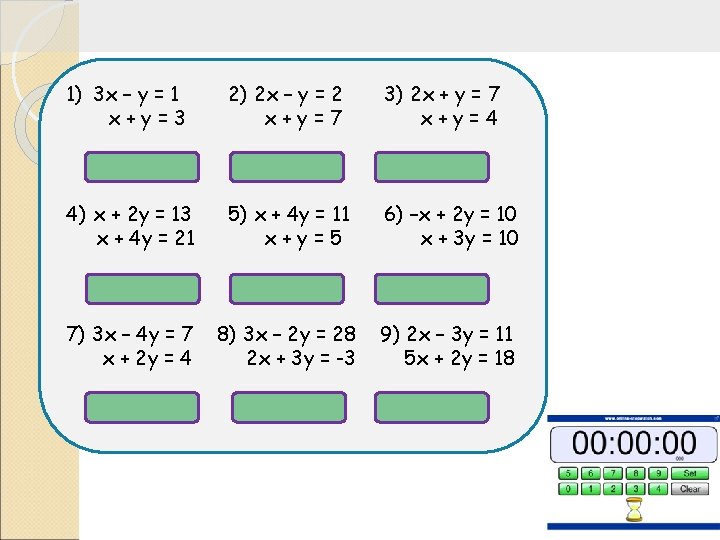
1) 3 x – y = 1 x+y=3 x = 1, y = 2 4) x + 2 y = 13 x + 4 y = 21 x = 5, y = 4 7) 3 x – 4 y = 7 x + 2 y = 4 x = 3, y=0. 5 2) 2 x – y = 2 x+y=7 x = 3, y = 4 5) x + 4 y = 11 x+y=5 x = 3, y = 2 8) 3 x – 2 y = 28 2 x + 3 y = -3 x = 6, y = -5 3) 2 x + y = 7 x+y=4 x = 3, y = 1 6) –x + 2 y = 10 x + 3 y = 10 x = -2, y = 4 9) 2 x – 3 y = 11 5 x + 2 y = 18 x = 4, y = -1

Lesson 2

28/11/2020 Solving Simultaneous Equations LO: To be able to solve Simultaneous Equations using the elimination method STARTER: Expand & Simplify: 7 x + 30 3(x + 4) + 4(x + 7) 12 y 2(3 y + 6) + 3(2 y – 4) -8 m -72 6(2 m – 10) – 4(5 m + 3)

Solving Simultaneous Equations – Example 1 Bronze: 15 (1) We have 2 unknowns: x and y SAME SIGN Solve: 6 x + 1 y = SUBTRACT 4 x + 1 y = 11 (2) Step 1: Eliminate the letter Step 2: To find y, we substitute with the same co-efficient x = 2 back into one of the (by SUBTRACTING in this original equations (equation 1) question)… 6 x + 1 y = 15 4 x + 1 y = 11 - 15 2 x = (6 x 2) + y = 15 12 + y = ( -12) 4 x =

Solving Simultaneous Equations – Example 1 Bronze: 15 (1) We have 2 unknowns: x and y SAME SIGN Solve: 6 x + 1 y = SUBTRACT 4 x + 1 y = 11 (2) Step 3: Check your answers using equation (2)… x= 2, y = 3 (4 x 2) + 3 = 11 8 + 3 = 11

Solving Simultaneous Equations – Example 3 DIFFEREN Bronze: We have 2 unknowns: x and y Solve: 4 x + 3 y = T SIGN 32 (1) ADD 5 x – 3 y = 13 (2) Step 1: Eliminate the letter Step 2: To find y, we substitute with the same co-efficient x = 5 back into one of the (by ADDING in this original equations (equation 1) question) (4 x 5) + 3 y = 32 4 x + 3 y = 32 5 x - 3 y = 13 + 9 x = - 20) 45 x = 3 y = 12 20 + 3 y = 32 (

Activity

Plenary Question Solve to find r and t. What is different here? 7 r + 6 t = 33 19 r – 30 t = -3

Lesson 3

28/11/2020 Solving quadratic simultaneous equations Always aim high! LESSON OBJECTIVES We are learning to: - Solve linear simultaneous equations. - Solve quadratic simultaneous equations.

TASK STARTER Solve the following simultaneous equations: 2) 6 x + y = 27 1) 6 x + y = 26 Signs different (+) 4 x + y = 11 Signs different (-) 2 x - y = 6 + 2 x = 16 8 x = 32 x = 8 x = 4 Substitute in x = 8 Substitute in x = 4 32 + y = 11 8 - y = 6 y = -21 y = 2 EXTENSION Solve the following simultaneous equation: 1) 3 x – 5 y = 5 x 3 Substitute in x = 3. 75 x 5 5 x – 3 y = 15 9 x – 15 y = 15 - 25 x – 15 y = 75 -16 x = -60 x = 3. 75 11. 25 - 5 y = 5 - 5 y = -6. 25 y = 1. 25 28/11/2020

EXAMPLE 1 Solve the following quadratic simultaneous equation. 1 2 Rearrange equation substitution for Make both brackets = 0 x x x Factorise quadratic 28/11/2020

QUADRATIC SIMULTANEOUS EQUATIONS EXAMPLE 2 Solve the following quadratic simultaneous equation. 1 2 When both equations are given in term of y, make = Rearrange to make the equation = 0 Factorise quadratic Make both brackets = 0 +3 -2 28/11/2020

QUADRATIC SIMULTANEOUS EQUATIONS TASK Solve these pairs of simultaneous equations: 1)(a) 2)(a) (b) (c) 3)(a) (b) (c) 4)(a) (b) (c) (d) (e) (f) (g) 28/11/2020

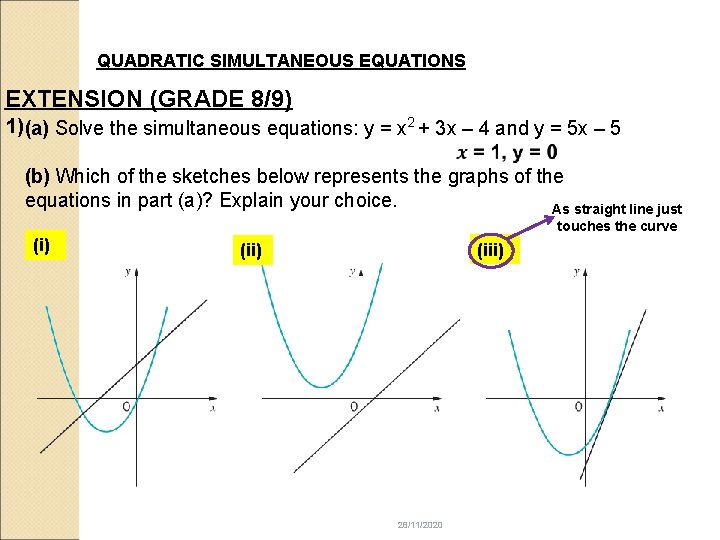
QUADRATIC SIMULTANEOUS EQUATIONS EXTENSION (GRADE 8/9) 2 1) (a) Solve the simultaneous equations: y = x + 3 x – 4 and y = 5 x – 5 (b) Which of the sketches below represents the graphs of the equations in part (a)? Explain your choice. As straight line just touches the curve (i) (ii) 28/11/2020

QUADRATIC SIMULTANEOUS EQUATIONS PLENARY Spot the mistake below: 1 2 Rearrange equation substitution for -3 -1 Make both brackets = 0 -3 -1 28/11/2020

How well do you understand the task? . I don’t understand I nearly understand 28/11/2020 I fully understand

Plenary Activity WWW (What Went Well) EBI (Even Better If) On your post it notes… Think about how you can improve your work. 28/11/2020

Lesson 4

28/11/2020 Setting up Simultaneous Equations

Test Your Understanding ? ? ?

If you are not told the letters to use, pick any.

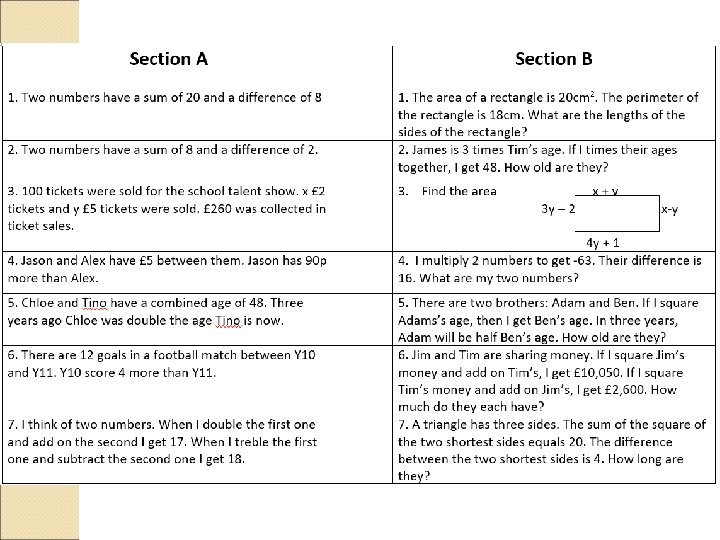
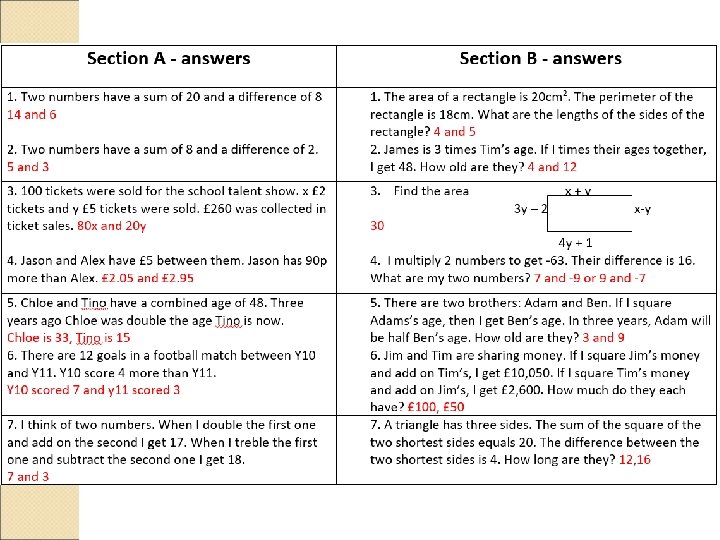
Exercise 2 1 N 1 3 a ? a b ? ? ? b N 2 c ? ? c ? 4 ? N 3 ? d 5 ? 2 [IMC 2004 Q 5] The sum of two numbers is 2. The difference between them is 4. What is their ? 6 ? ? ?

Exercise 3 Use substitution only to solve the following simultaneous A equations. 5 1 a 2 ? b C B ? c ? ? ? N 1 3 ? d ? e ? ? 4 £ 13 £ 19 £ 17 N 2 What is the cost of a cat? £ 1 ? ?

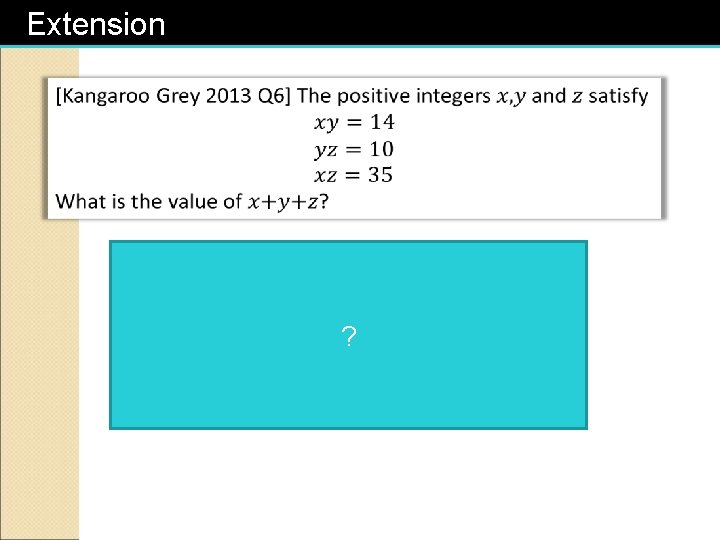
Extension ?

t s e o i s i v e R u Q n s n io

Questions You must now go through all the questions that are in the lessons and ensure you complete all of them. You should be doing the questions as you go through each lesson, so if they are already completed you don’t have much to do other than go through them and check answers.