Introduction to Z Notation 1 Z Notation First

Introduction to Z Notation 1

Z – Notation? • First off – its pronounced Zed – After the Zermelo-Fränkel set theory • It is a set of conventions for presenting mathematical text, chosen to make it convenient to use simple mathematics to describe computing systems. 2

Z – Notation? • It is targeted to clarify and streamline the specification and requirement process • Z is a “specification” language based on typed sets, relations, and functions to express: – What are the functionalities of the system – And what the desired results are 3

Z – Notation? • Thus Z is a declarative language - - meaning that it is non-procedural (not like Java or C) • Z “notation” developed at the Programming Research Group at Oxford University for recording, in precise way, some of the many decisions that are made in the course of software development. 4

Z – Notation? • Z is Based on the standard mathematical notation n The mathematical notation of Z consists of a small core, Supplemented by a larger collection of useful objects and operators called the Z mathematical tool-kit. 5

Z Mathematical Toolkit n The tool-kit is not software, it is a collection of mathematical theories: definitions and laws concerning objects such as sets, tuples, relations, functions, sequences and their operators. 6

Z Mathematical Toolkit • In Z we use these mathematical objects to model data structures and other components of computing systems. 7

Z Mathematical Toolkit • The tool-kit plays somewhat the same role in Z that a standard library of types and functions does in an executable programming language. 8

Z Specification • Z specifies a system using: • Mathematically defined data types • Decompositions called Schemas 9

Z Specification A schema describes both the static and the dynamic aspects of a system. Static Individual states Invariants maintenance Dynamic State Transitions Events (operations) Transformations (relationship of input to output) 10

Z Specification • The Z language also allows us to combine and relate separately defined schemas in a mathematically logical fashion. 11

Z Specification To learn how to speak any language, we first need to learn some vocabulary and some simple rules of grammar. Both the vocabulary and the grammar of Z should be largely familiar to you. Over the next few pages, we will cover some of these (without necessarily going into the details and subtleties of their definitions and uses). 12

Z Specification S T S is strictly contained in T (S T) S T S is not contained in T Set of intersection of S and T Set of the union of S and T PS Powerset of S: the set of all subsets of S FS Finite powerset of S: the set of all finite subsets of S SS The distributed intersection of all sets in SS The distributed union of all sets in SS Or { } The null or empty set 13

Z Specification ST Difference: elements that are in S but not in T #S Size or cardinality: number of elements in S {D|p. t} Set of t’s such that given declaration D, P holds Logic true, false logical constants P not P 14

Z Specification P Q conjunction: “P and Q” P Q disjunction: “P or Q” P Q implication: “If P then Q” P Q equivalence: : “If P then Q and if Q then P” t=r term t is equal to term r term t is not equal to term r, that is: (t=r) Predicates: x: T. P for all x of type T, P holds x: T. P there exists an x of type T, for which P holds 15

Z Specification Relations: X Y the set of ordered pairs of X’s and Y’s X Y the set of relations from X to Y; = = P(X Y) x. Ry x is related to y by R; (x, y) R dom R the domain of relation R; = ={x: X | ( x: X. x R y). x} ran R the range of a relation R; = ={y: Y | ( x: X. x R y). y} S R the relation R is domain restricted to S R S the relation R is range restricted to S R~ the inverse of R 16

Z Specification Functions: X Y the set of partial functions from X to Y = ={f: X Y | ( x: X | x dom f. ( 1 y: Y. x f y))} X Y the set of total functions from X to Y = ={f: X Y| dom f = X. f} fx or f(x) function f is applied to x 17

Z Specification Sequences: seq X the set of sequences with elements drawn from X = ={S: N X | dom S= 1…#S} seq 1 X set of non-empty sequences of X iseq X set of non-duplicate sequences of X #S the length of sequence X <> the empty sequence <x 1, …xn> the sequence of x 1 through to xn 18

Z Specification Schema decorations: | name: T name is a constant of type T item ? : T item is an input or accepts input item !: T item is an output or holds an output item’ new state of item after change (item) the schema effects change on item Ξ (item) item is left unchanged by schema 19

Z Alphabet and Lexical elements • Z has both forms: – text and – graphical • Z identifiers are constructed from letters, digits, and the “_” character. – Upper and lower case are distinct – No length restriction – First character must be a letter; it may also be a special symbol (state change) or (no state change). – May end with special characters of ? , !, '. 20

Z-Schema • A schema is a structuring mechanism, a diagrammatic presentation, that allows the specification of: a) data b) operations that access that data • The Z- schema may be defined in two ways: – graphical form – text form 21

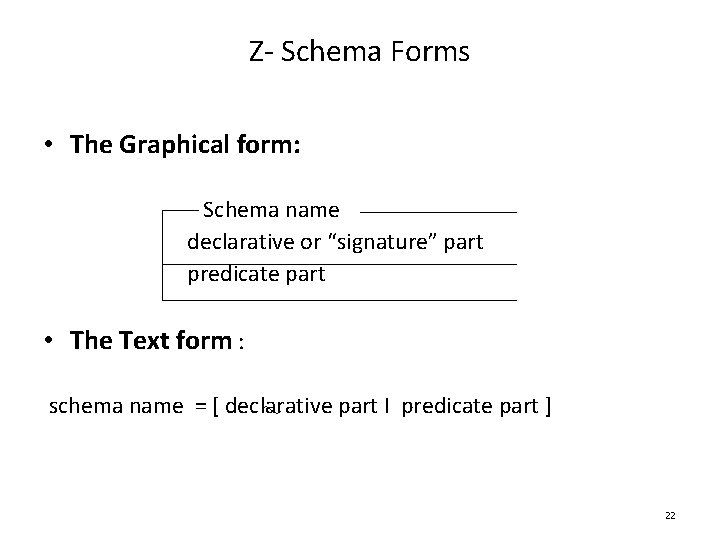
Z- Schema Forms • The Graphical form: Schema name declarative or “signature” part predicate part • The Text form : schema name = [ declarative part I predicate part ] 22

Z-Schema “Parts” • The declarative or the “signature” part: – Introduces the identifiers (or variables) – And assigns them the set type – Each line statement is “assumed” to be terminated with ; • The predicate part refers to the identifiers in the declaration part or some global identifier in other schemas 23

Examples of Schemas Graphical form: B_Team Member : [students] Team : IP students # (Team) < 11 - Schema is named B_Team -Member is of type “students” (which is defined elsewhere) -Team is a subset (type) of the power set of students - Cardinality of Team is < 11 Text form: B_Team = [ Member: students; Team: IP students I # (Team) < 11 ] 24

Z types and declarations • Z is “strongly” typed --- that is , every identifier must be declared. • Z has 3 “types” : – built-in : Z (integers), N (natural numbers), N 1 ( positive integers) – basic : application dependent set (assumed to be pre-defined) – free type : enumerations – ( note that real numbers and characters are not part of built-in ) • Basic type may be written in bracket, [ ] : – [ students ] , [ employees ] , [ books ] – Or [ students, employees, books ] • Free type may be written as enumerations: – Students : : = { William I Shilpa I Harish I Carolyn I Ahmed I Joel } – and then identifiers x and y may be declared: • x , y : Students 25

Global constant and variable • Global constant is declared with the “==“ symbol: minimum == 0 • Global “variable” that has some constant associated with it may be declared via an “axiomatic description” : age : N age < 150 The global “variable”, age, is really some “constant” that has a value less than 150 and age may be used globally. Axiomatic description is like the schema without the top and bottom lines. 26

More Sophisticated Types • The variables in the signature may introduce any set theoretic type, including any higher order functions. The symbols used to depict relations and different types of functions are : – – – – a relation a partial function a total function a partial injection a total injection a partial surjection a total surjection a bijection 27

How To Model A System • Z decomposes specifications into manageably sized module’s, called schemas • Schemas are divided into 3 parts: • A State • A collection of state variables and their values • There also some operations that can change its state 28

How To Model A System • A state is a situation • We model a state as an assignment of values to a collection of named variables. • States can represent assumptions (preconditions), goals (results, postconditions), or safety requirements (invariants). 29

How To Model A System • State can be divided into fixed configuration (constants) and volatile components (state variables). • Programming languages do not describe states directly; they can only describe state transitions. 30

How To Model A System – Z state variables are like instance variables and the operations are like methods; – Z even provides a kind of inheritance. 31

General Guideline for Z-Schema Specification • Static portion: – The states (or variables and constants) the system can have. – Invariant characteristics • “Dynamic” portion: – The functions (operations) that the system performs – The relationships among the inputs, outputs and other variables – The change of states in terms of “pre” and “post” conditions 32

How To Model A System • Z is also a natural fit to object-oriented programming. – You can also use Z in a functional style, among others – There are some object oriented languages that extend Z such as Object-Z. 33

How To Model A System n n Object-Z, Z++ are two languages that extend Z by the addition of language constructs resembling the object-oriented paradigm, most notably, classes. Other object-oriented notions such as polymorphism and inheritance are also supported. 34

How To Model A System • Schema Model Name Some variables are declared. As well as state transitions. Relationship between the values of the variables 35

Z- Schema inclusion • A feature of Z-schema is that it allows the incremental and independent development of schema(s) – There is a mechanism for one schema to refer to another schema via schema inclusion. – Schema inclusion is accomplished by stating the name of the referred to schema in the signature part of the referring schema. – The result of schema inclusion is that : • the refered to schema’s signature portion is included into the signature portion of the referring schema, and • the predicate portion of the referred to schema is logically conjoined with the predicates of the referring schema The schema inclusion is a bit like the “inheritance” or “include” functions 36

Schema Inclusion Example Temp_Users SPSU_Users : : = Students I Faculty I Administrators temp_u, users : IP SPSU_Users n_of_days : N 1 Note : exp_days is a exp_days : users n_of_days total function temp_u users temp_u = { u: users I ran(exp_days) < 30 u} Users Temp_Users reg_u : IP SPSU_Users reg_u = { u : users I ran(exp_days) >= 30 users = temp_u U reg_u u} Note : Temp_Users is included in the Users schema. So we can use all the terms from Temp_Users 37