Introduction to Visual BASIC Loops Q What is

Introduction to Visual BASIC Loops

Q: What is a Loop? z. A control structure that allows for a sequence of steps to be repeated a certain number of times z. This sequence of steps is called the body of the loop

Q: What is a Loop? z. There are three basic loop structures in programming: y. For y. While y. Repeat

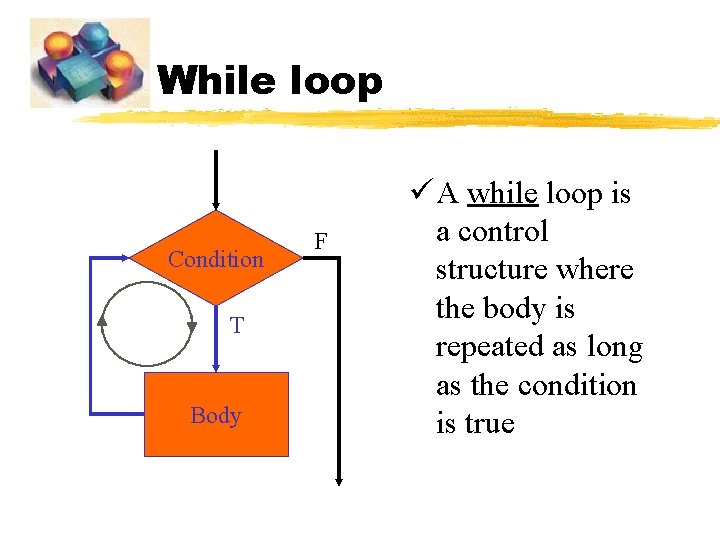
While loop Condition T Body F ü A while loop is a control structure where the body is repeated as long as the condition is true

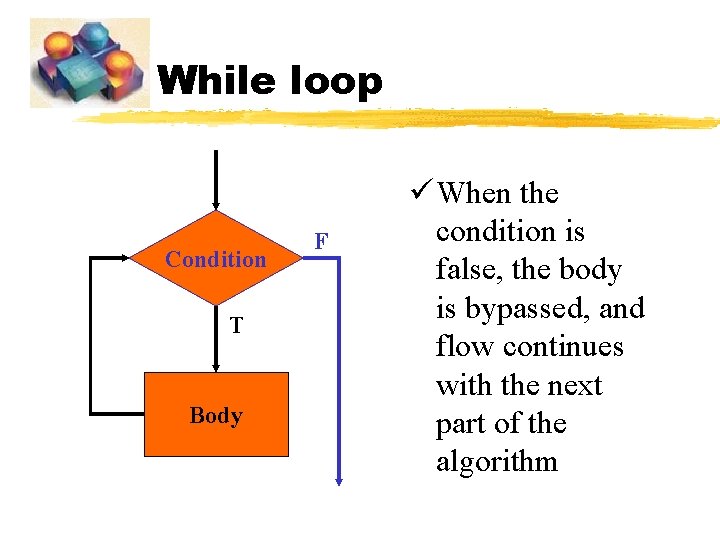
While loop Condition T Body F ü When the condition is false, the body is bypassed, and flow continues with the next part of the algorithm

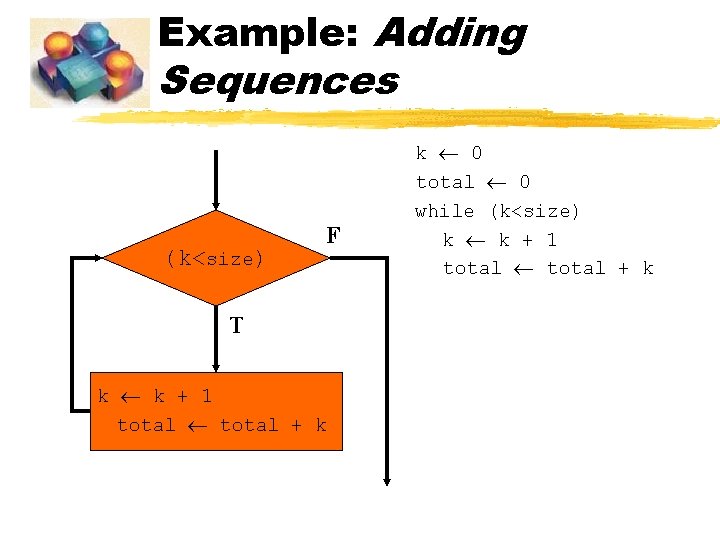
Example: Adding Sequences (k<size) F T k k + 1 total + k k 0 total 0 while (k<size) k k + 1 total + k

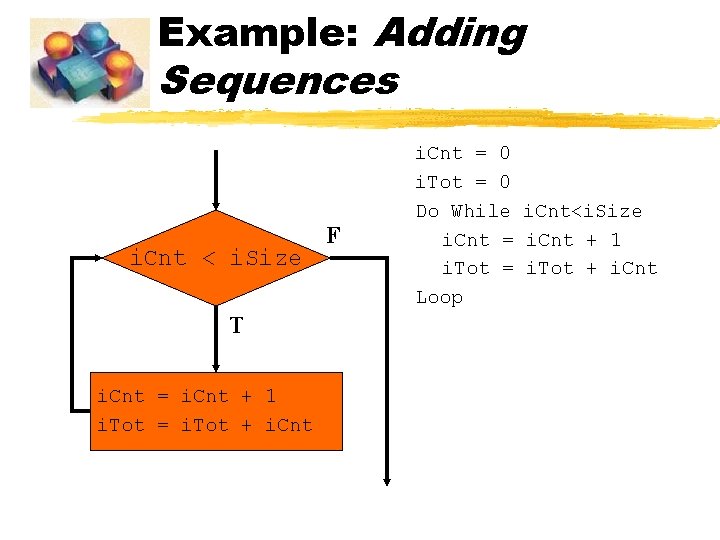
Example: Adding Sequences i. Cnt < i. Size T i. Cnt = i. Cnt + 1 i. Tot = i. Tot + i. Cnt F i. Cnt = 0 i. Tot = 0 Do While i. Cnt<i. Size i. Cnt = i. Cnt + 1 i. Tot = i. Tot + i. Cnt Loop

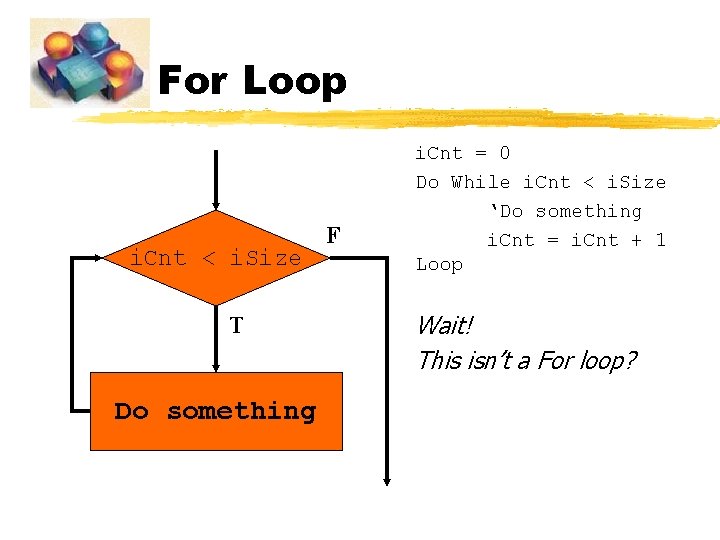
For Loop i. Cnt < i. Size T Do something F i. Cnt = 0 Do While i. Cnt < i. Size ‘Do something i. Cnt = i. Cnt + 1 Loop Wait! This isn’t a For loop?

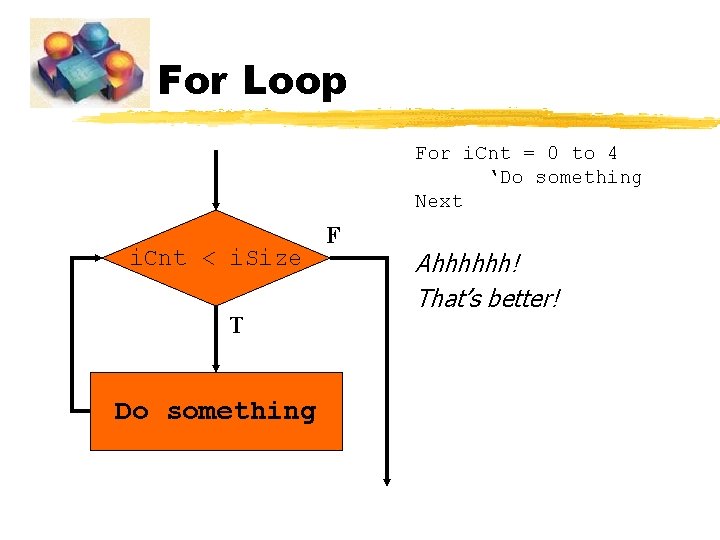
For Loop For i. Cnt = 0 to 4 ‘Do something Next i. Cnt < i. Size T Do something F Ahhhhhh! That’s better!

Exercise z. The function factorial (n!) is defined as the product of the integers 1 through n. z. Create two functions to compute n!, the first version using a for loop and the second using a while loop.

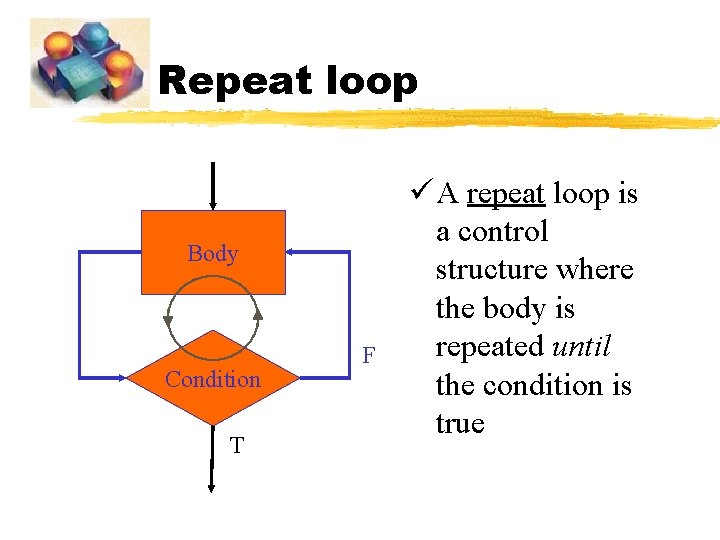
Repeat loop Body Condition T F ü A repeat loop is a control structure where the body is repeated until the condition is true

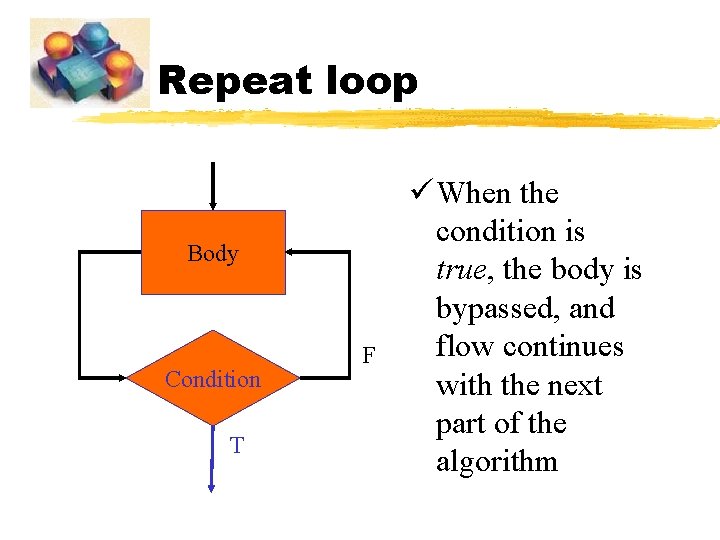
Repeat loop Body Condition T F ü When the condition is true, the body is bypassed, and flow continues with the next part of the algorithm

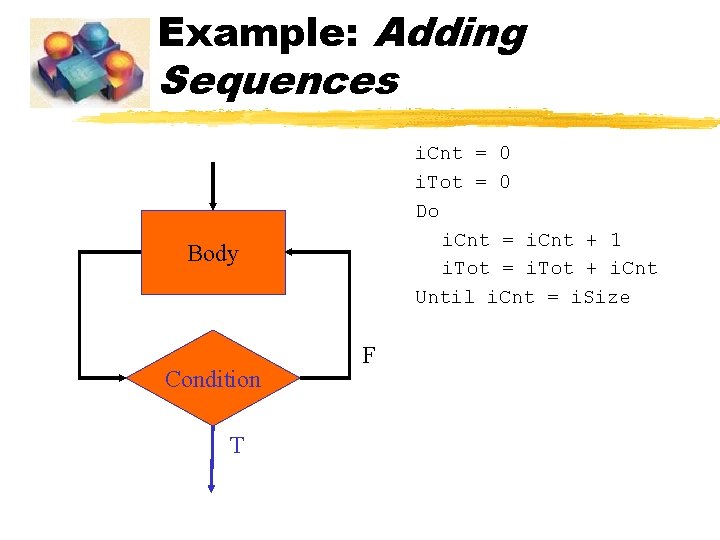
Example: Adding Sequences i. Cnt = 0 i. Tot = 0 Do i. Cnt = i. Cnt + 1 i. Tot = i. Tot + i. Cnt Until i. Cnt = i. Size Body Condition T F

Recursion z. When a subroutine or function calls itself Private Function sum. It (N As Integer) As Integer Dim i. Total as Integer If N > 0 Then sum. It = sum. It(N – 1) + N Else Recursive sum. It = N call End Function

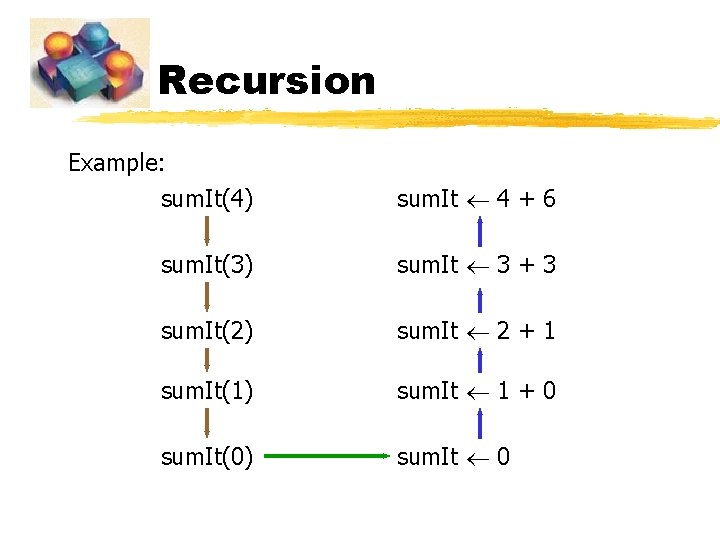
Recursion Example: sum. It(4) sum. It 4 + 6 sum. It(3) sum. It 3 + 3 sum. It(2) sum. It 2 + 1 sum. It(1) sum. It 1 + 0 sum. It(0) sum. It 0

Recursion z. But … there’s only so far down we can go z. Question : How many recursive calls would it take to evaluate sum. It(10000)?

Recursion z. Each time you make a recursive call, the state of the calling routine is saved on the program stack (part of memory) z. But … the stack is only so big z. You can run out of space!

Recursion z. A better solution is to re-write the routine using a loop instead of recursion z. Any ideas?