Introduction to Turing Machines 0 01 1 10











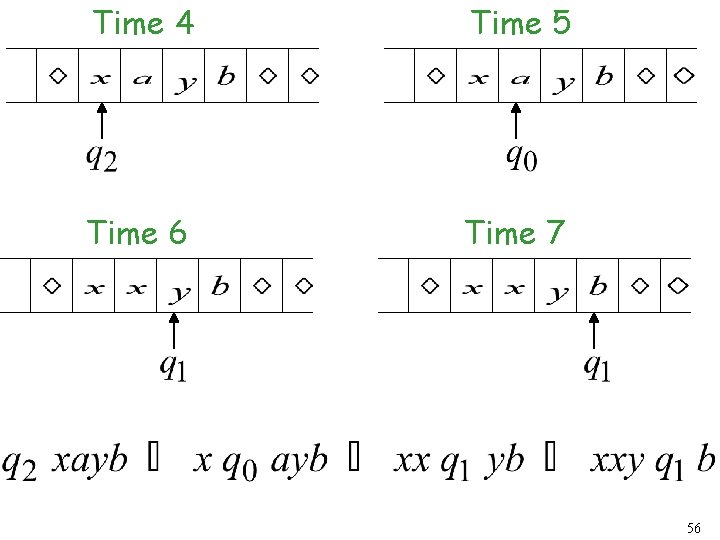




















- Slides: 102

Introduction to Turing Machines 0 01 1 10 1 1 1 0 0 0 1

Alan Turing -- 1912 – 1954 • Mathematician, a computer scientis • Influantial • Development of computer sciences • provided an influential formalisation • of the concept of the algorithm • and computation with the • Turing Machine • Turing Test contribute to the debate of AI • Can machines think? • • One of the 100 more imp. People in 20 th century 21 st on BBC nation wide poll of the 100 Greatest britons http: //www. turing. org. uk/turing/ http: //en. wikipedia. org/wiki/Alan_Turing/ 2

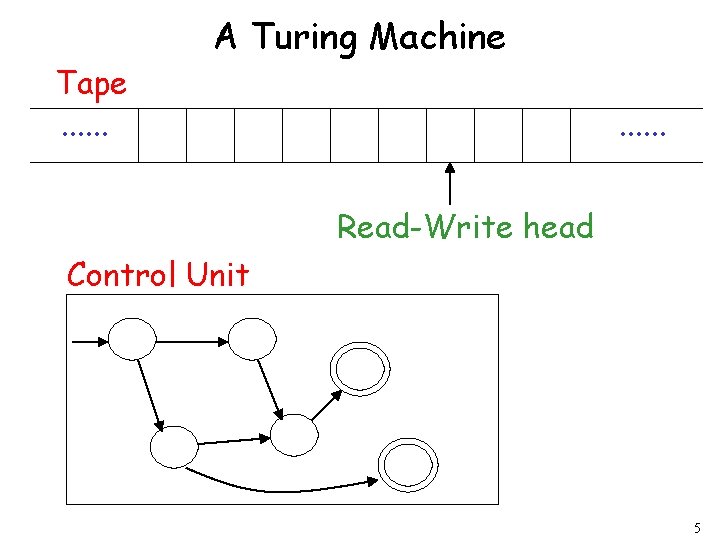
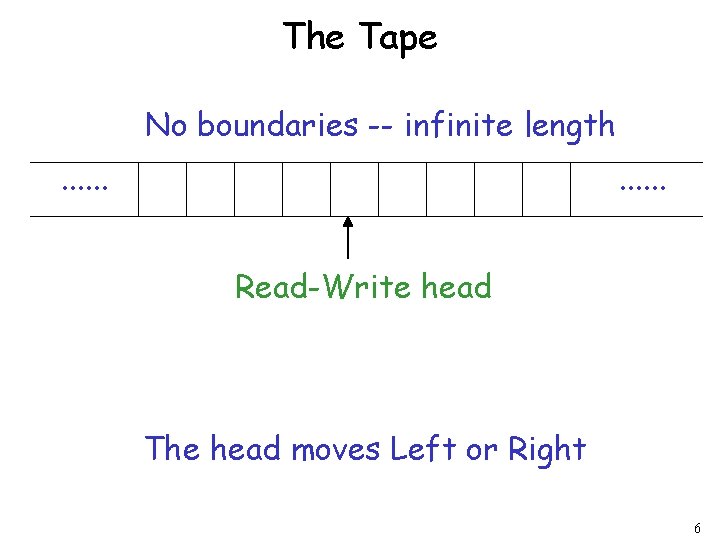
The Turing Machine 10 01 1 10 1 1 1 0 0 0 A TM consists of an infinite length tape, on which input is provided as a finite sequence of symbols. A head reads the input tape. The TM starts at start state s 0. On reading an input symbol it optionally replaces it with another symbol, changes its internal state and moves one cell to the right or left. 3

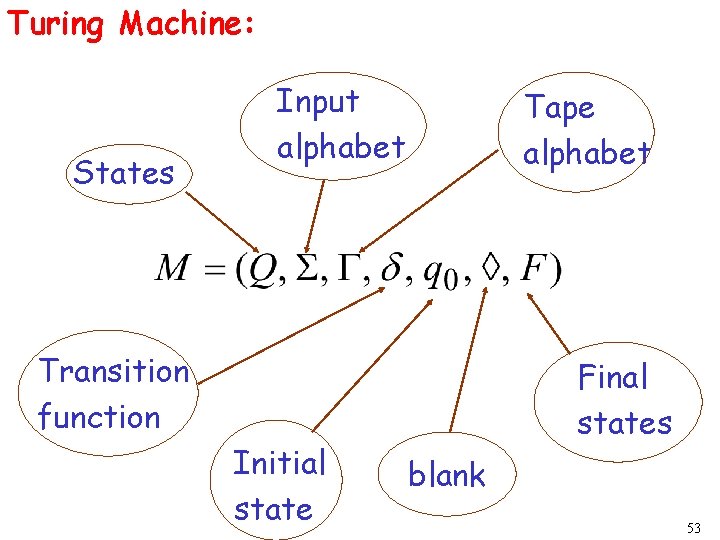
The Turing Machine A TM is defined as: TM = <S, T, s 0, d, H> where, S is a set of TM states T is a set of tape symbols s 0 is the start state H S is a set of halting states d : S x T x {L, R} is the transition function 4

Tape. . . A Turing Machine. . . Read-Write head Control Unit 5

The Tape No boundaries -- infinite length. . . Read-Write head The head moves Left or Right 6

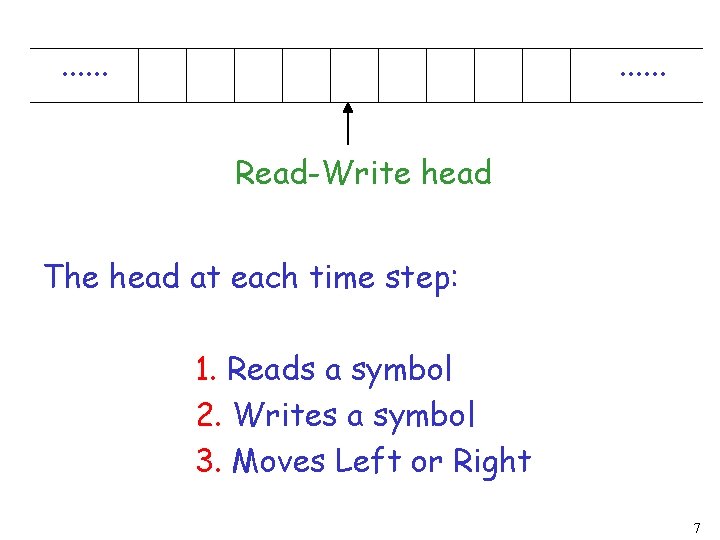
. . . Read-Write head The head at each time step: 1. Reads a symbol 2. Writes a symbol 3. Moves Left or Right 7

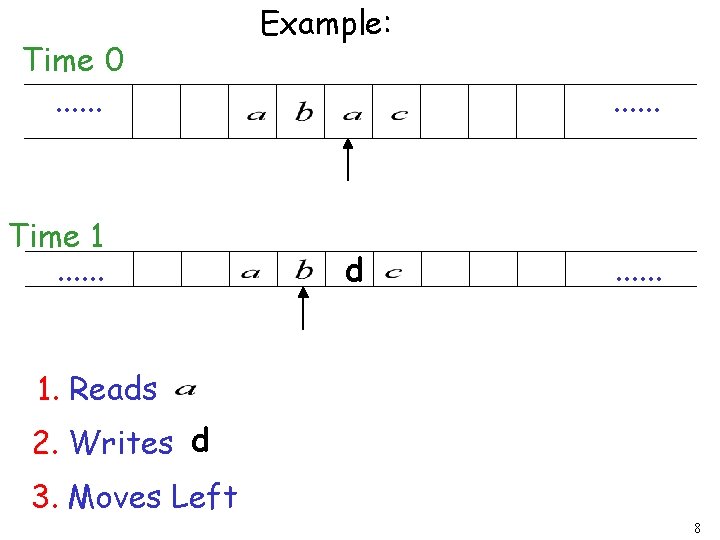
Time 0. . . Time 1. . . Example: . . . d . . . 1. Reads 2. Writes d 3. Moves Left 8

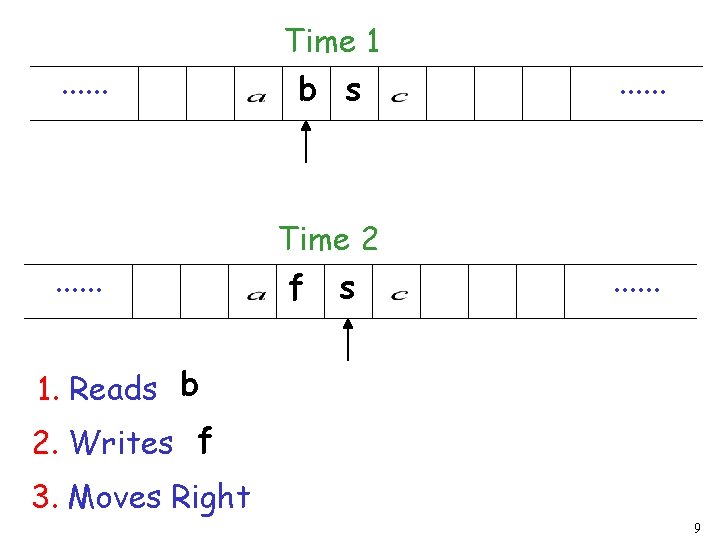
. . . Time 1 b s Time 2 f s . . . 1. Reads b 2. Writes f 3. Moves Right 9

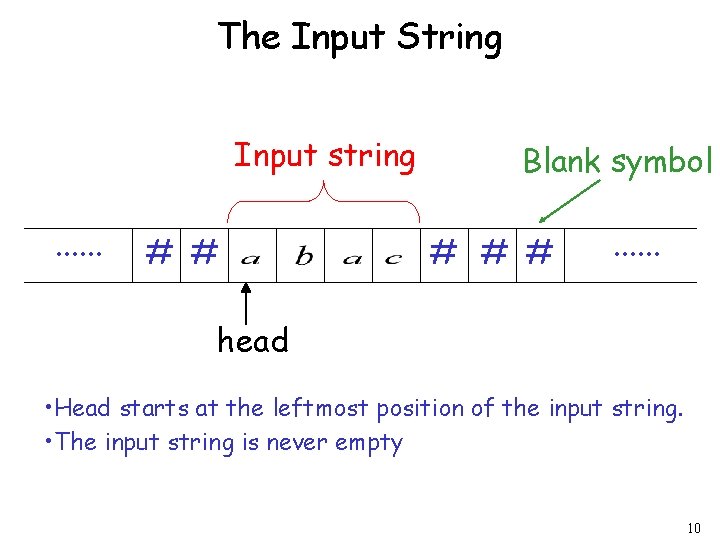
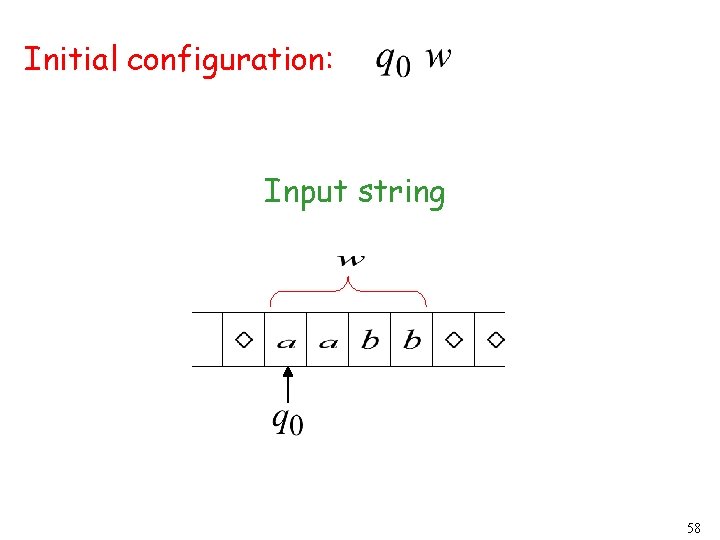
The Input String Input string. . . # # Blank symbol # # # . . . head • Head starts at the leftmost position of the input string. • The input string is never empty 10

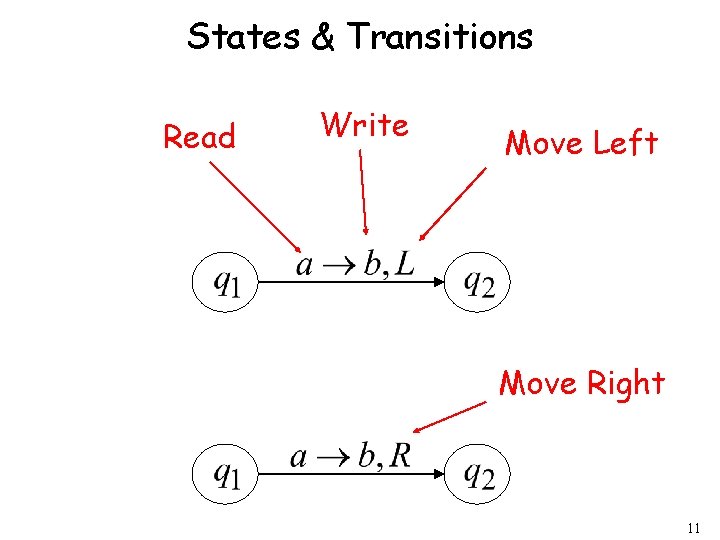
States & Transitions Read Write Move Left Move Right 11

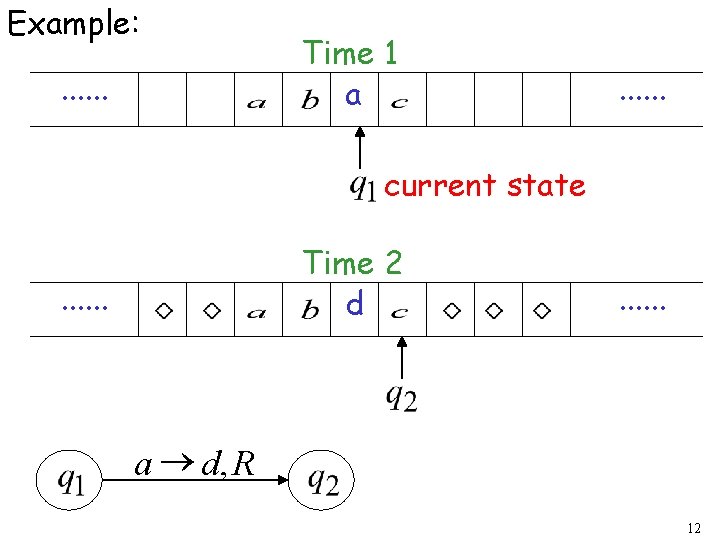
Example: . . . Time 1 a . . . current state Time 2 d . . . a ® d, R 12

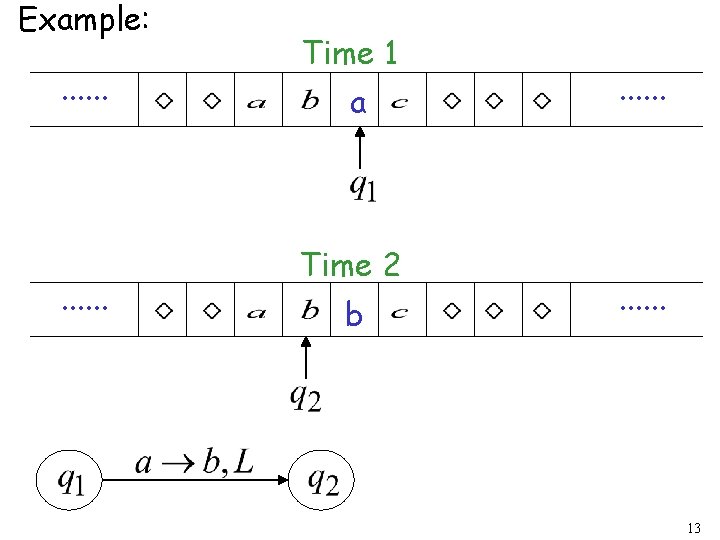
Example: . . . Time 1 a Time 2 b . . . 13

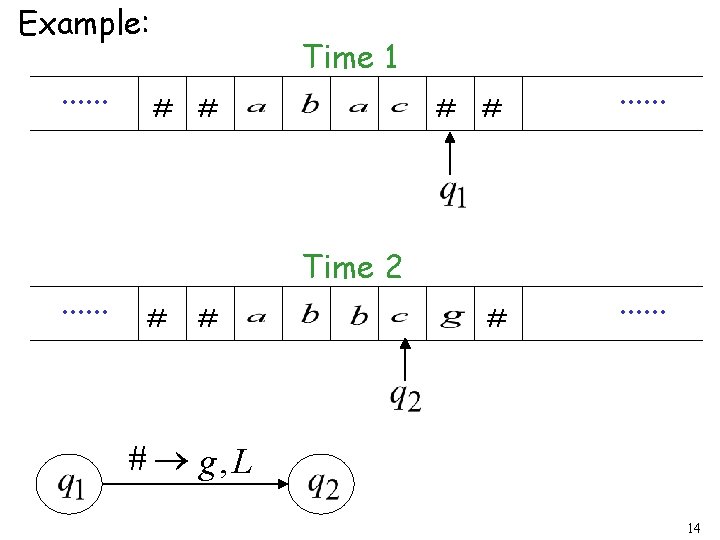
Example: . . . Time 1 # # . . . Time 2 # # # ® g, L 14

Determinism Turing Machines are deterministic Allowed Not Allowed No lambda transitions allowed 15

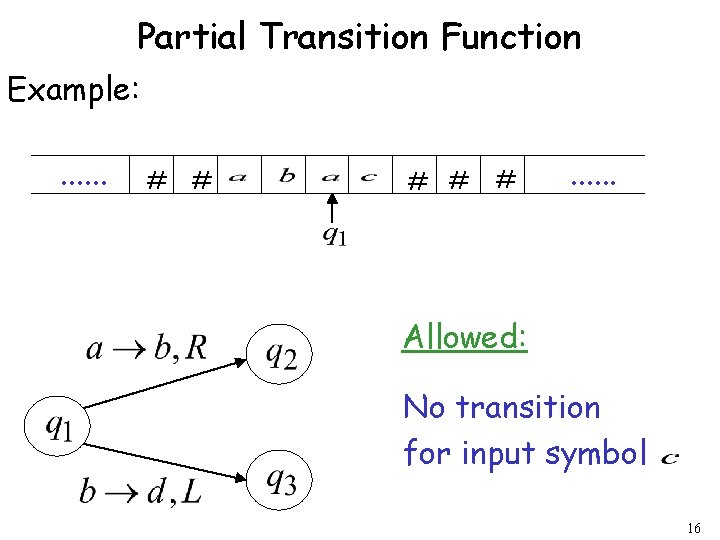
Partial Transition Function Example: . . . # # # . . . Allowed: No transition for input symbol 16

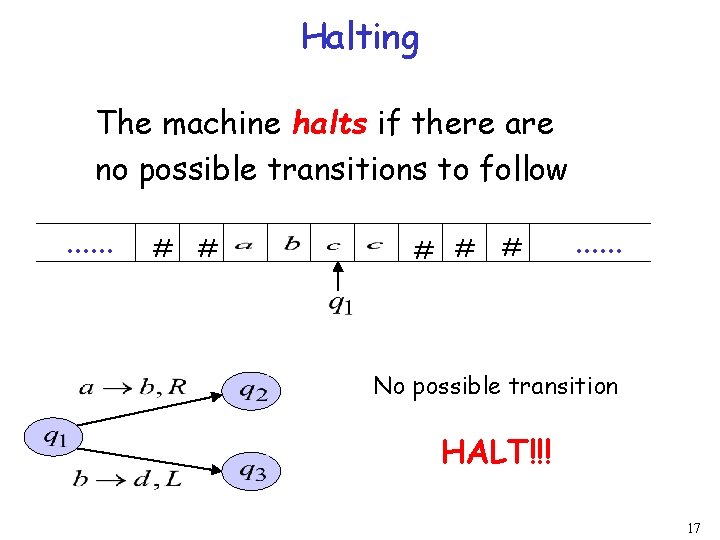
Halting The machine halts if there are no possible transitions to follow. . . # # # . . . No possible transition HALT!!! 17

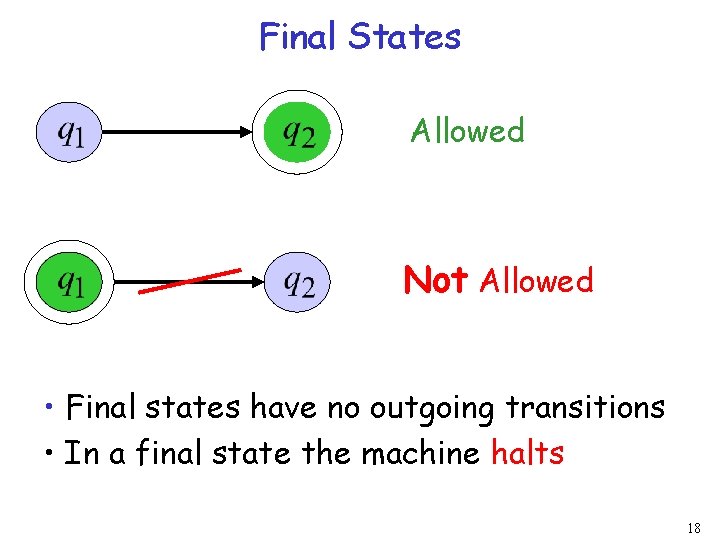
Final States Allowed Not Allowed • Final states have no outgoing transitions • In a final state the machine halts 18

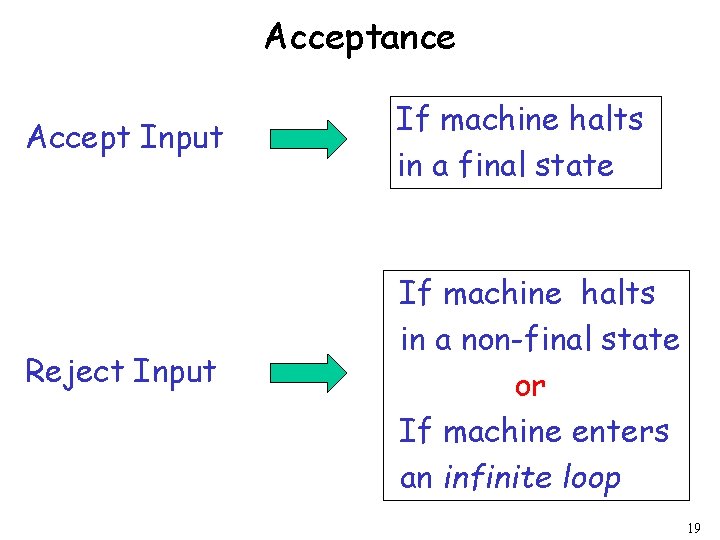
Acceptance Accept Input If machine halts in a final state Reject Input If machine halts in a non-final state or If machine enters an infinite loop 19

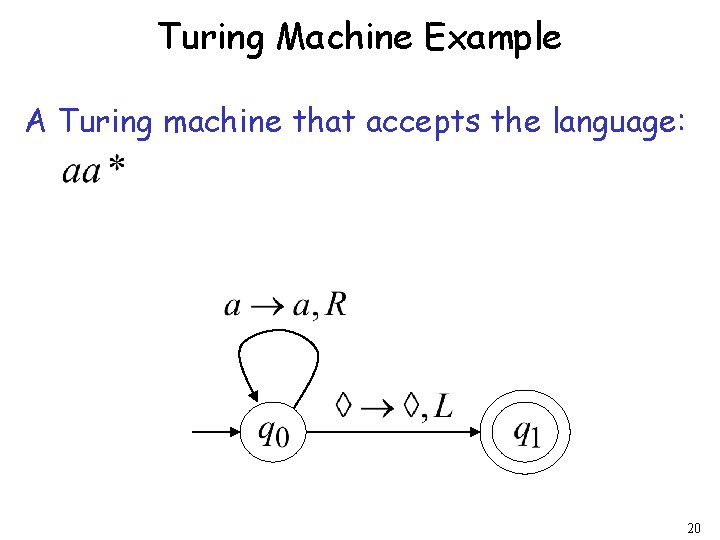
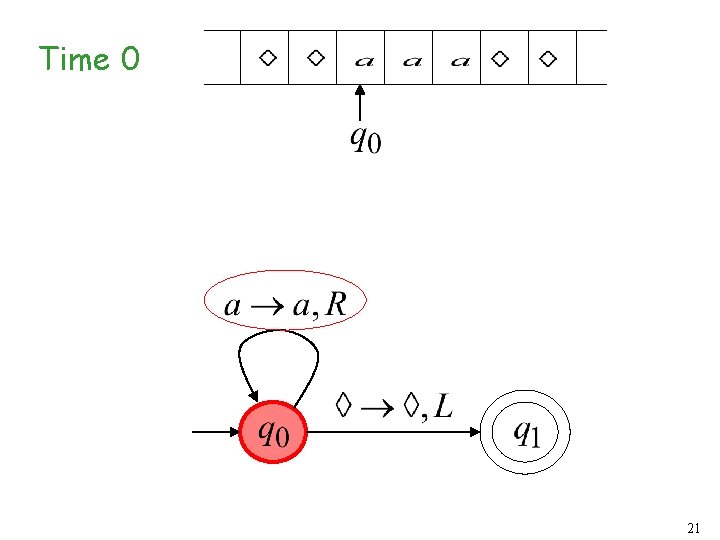
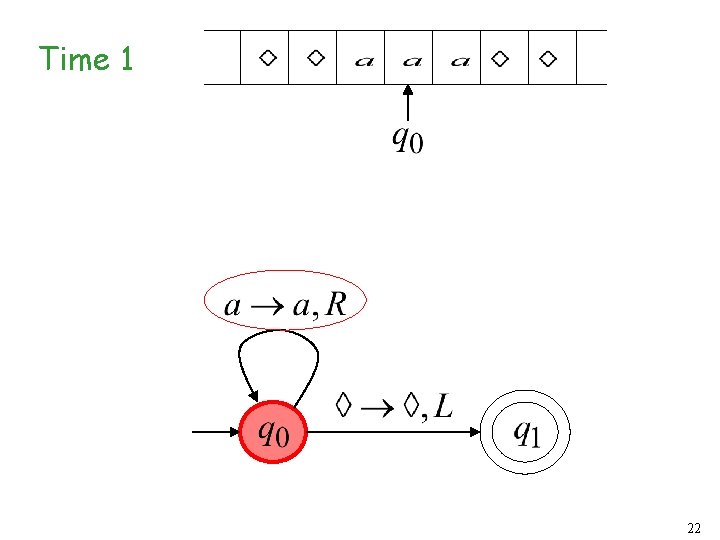
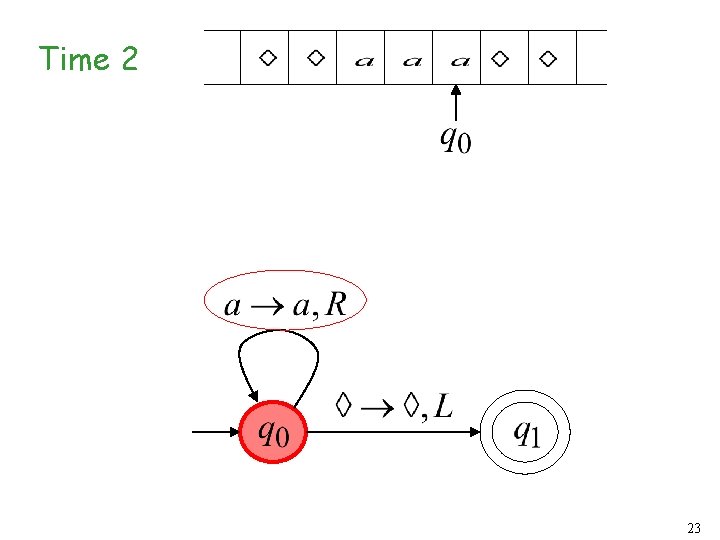
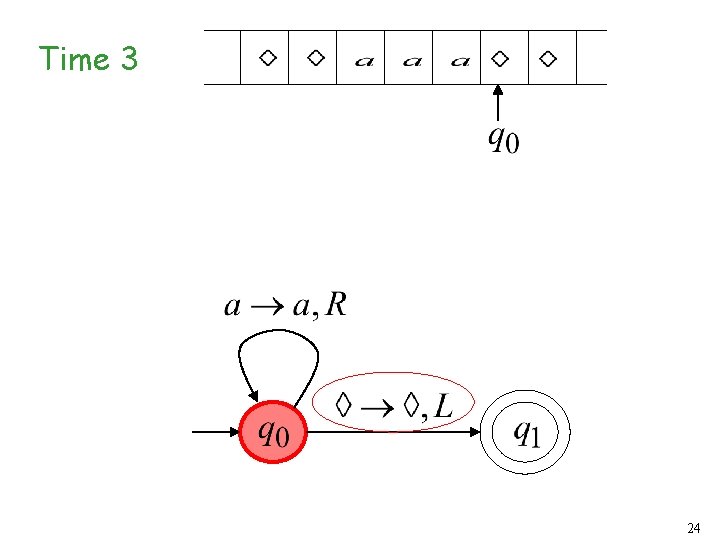
Turing Machine Example A Turing machine that accepts the language: 20

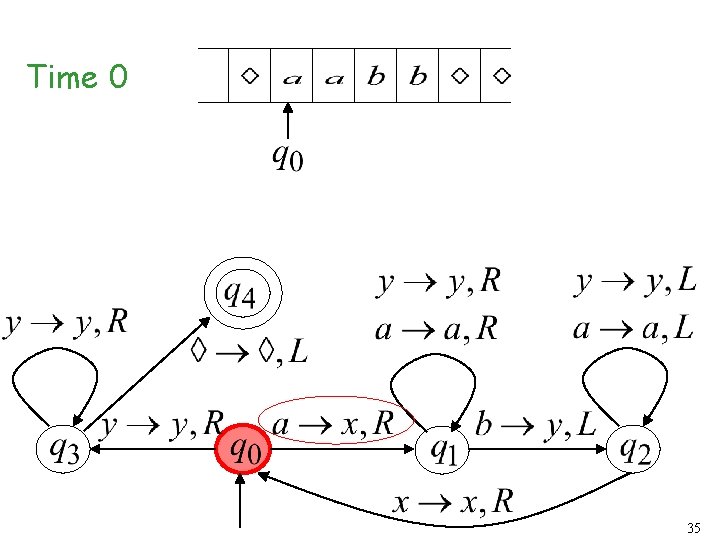
Time 0 21

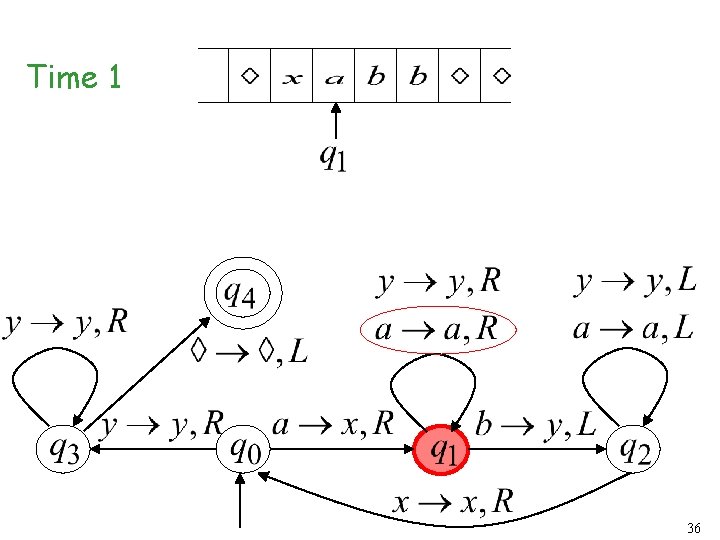
Time 1 22

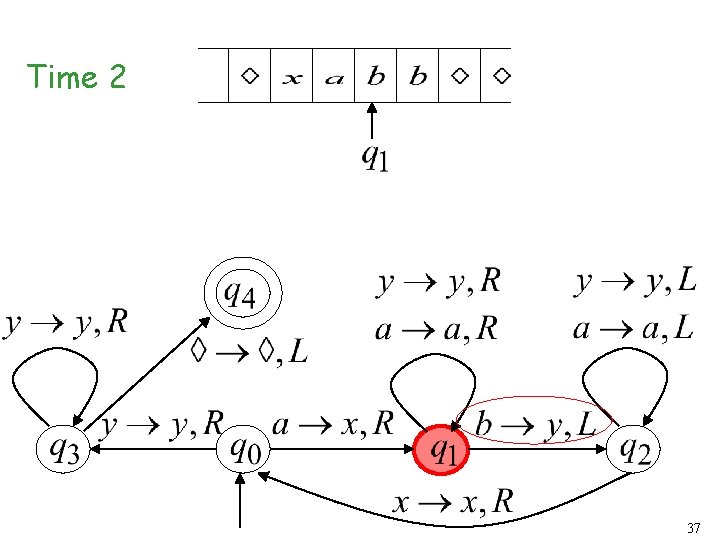
Time 2 23

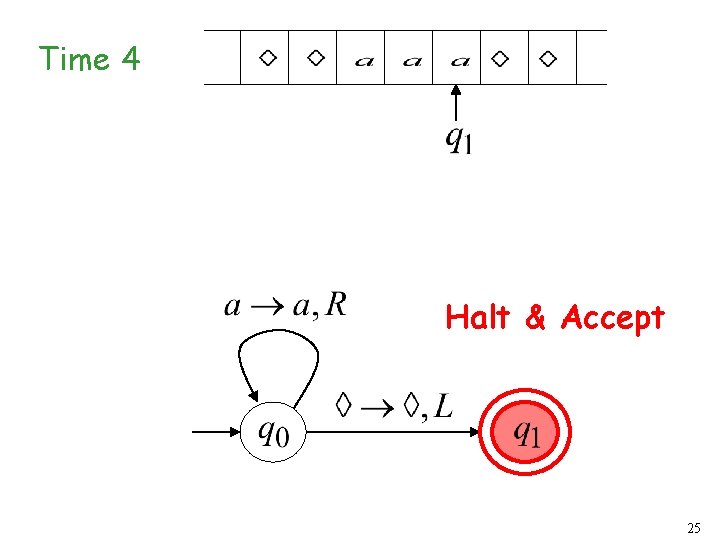
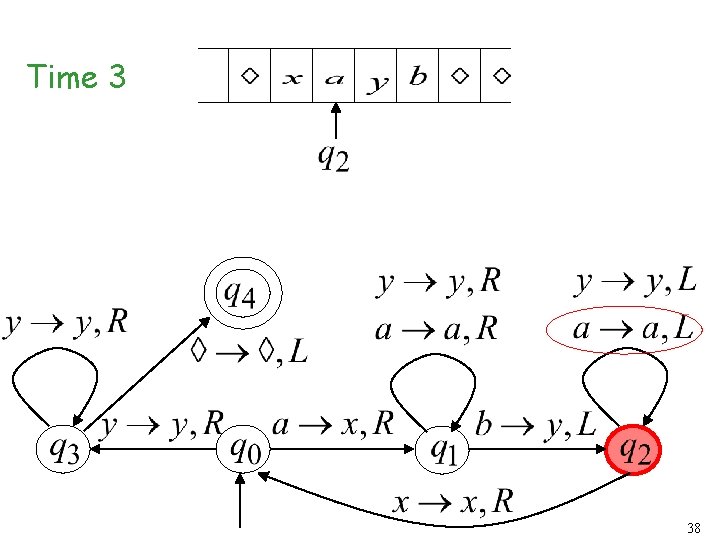
Time 3 24

Time 4 Halt & Accept 25

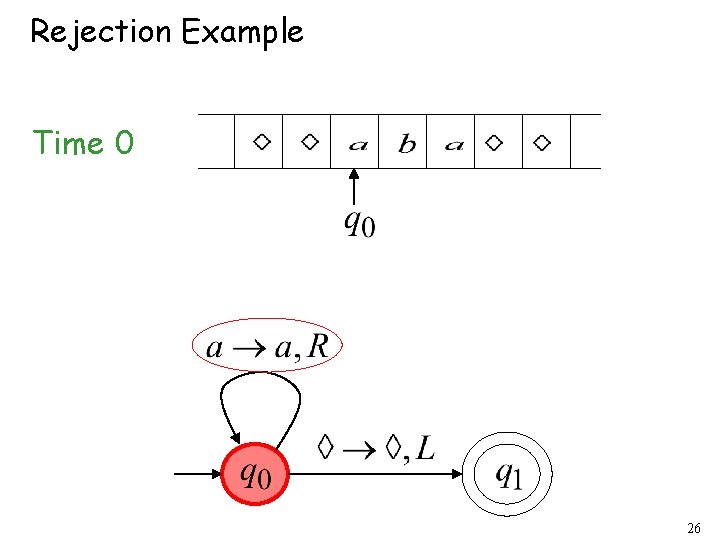
Rejection Example Time 0 26

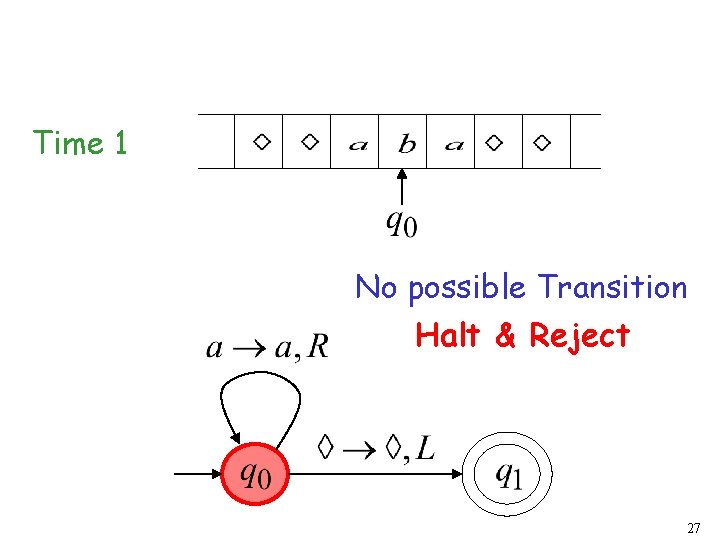
Time 1 No possible Transition Halt & Reject 27

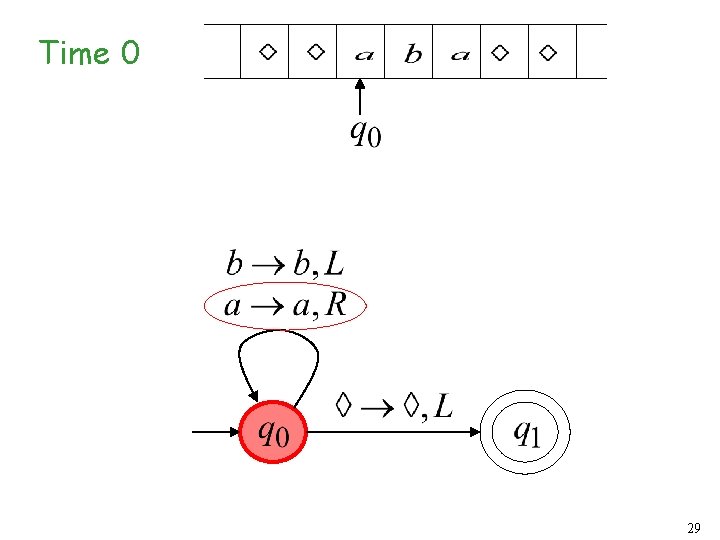
Infinite Loop Example A Turing machine for language 28

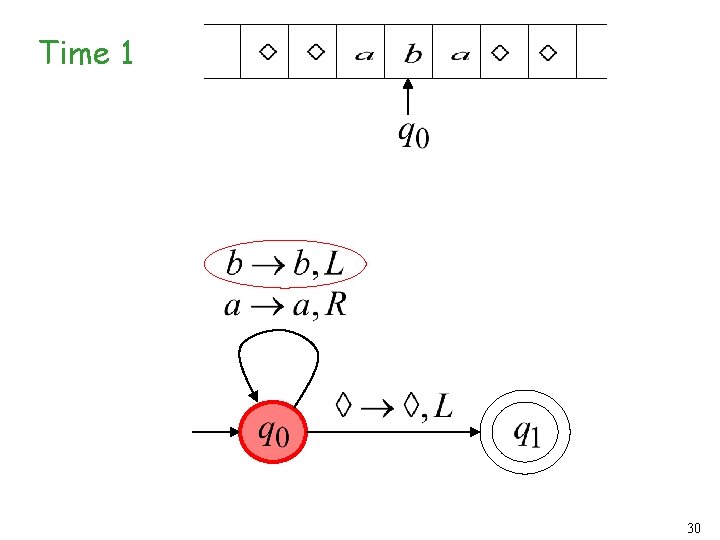
Time 0 29

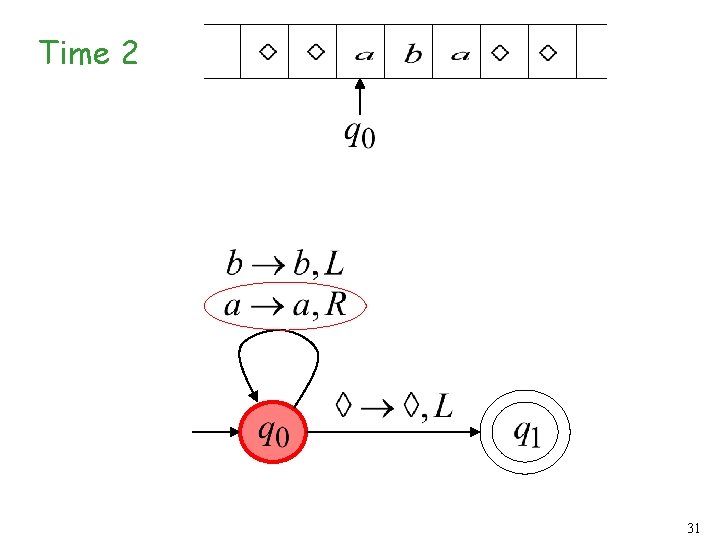
Time 1 30

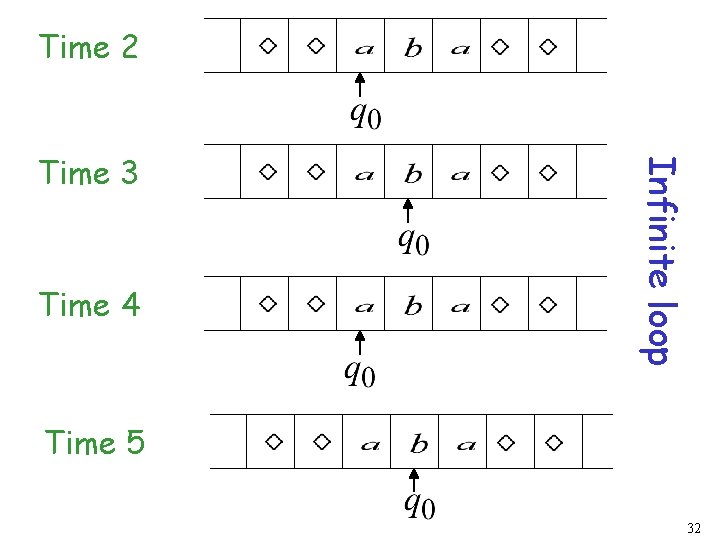
Time 2 31

Time 2 Time 4 Infinite loop Time 3 Time 5 32

Because of the infinite loop: • The final state cannot be reached • The machine never halts • The input is not accepted 33

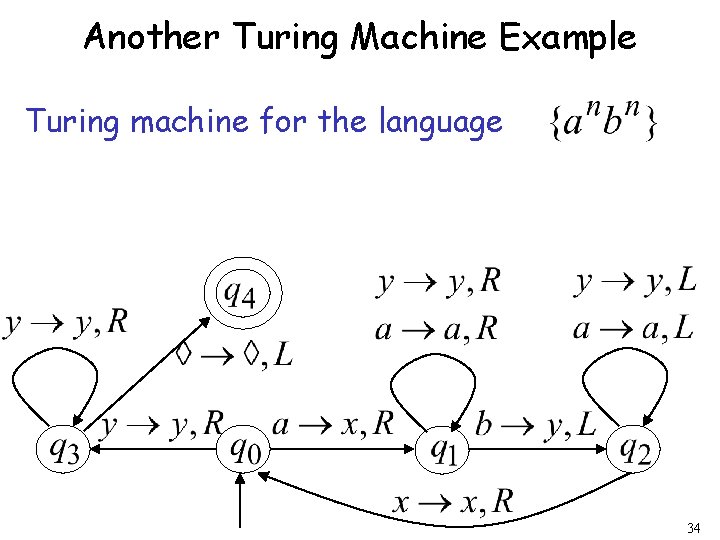
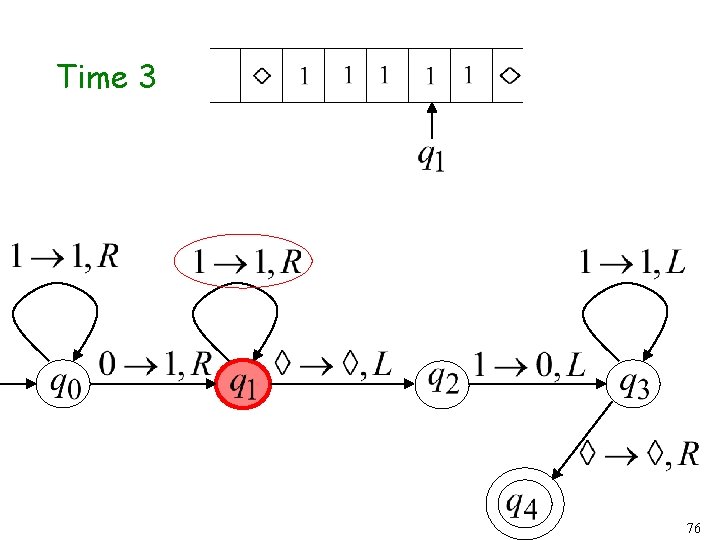
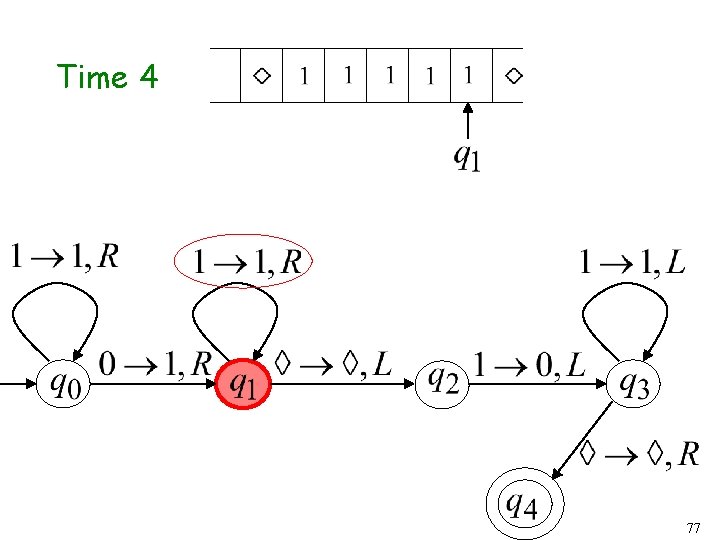
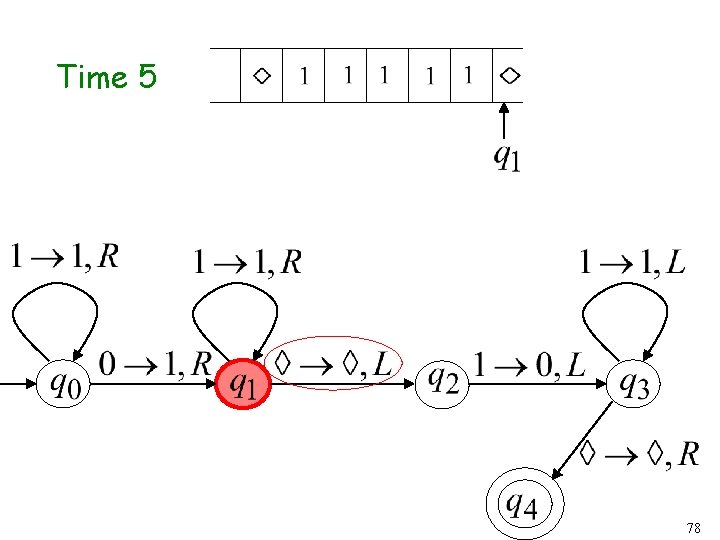
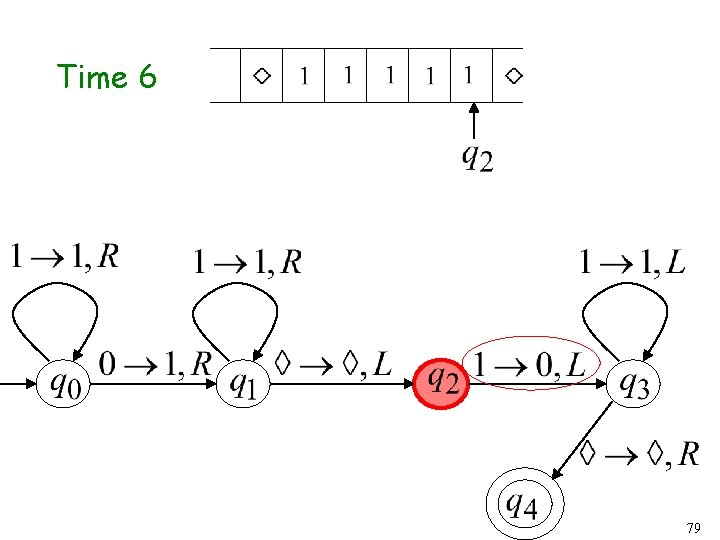
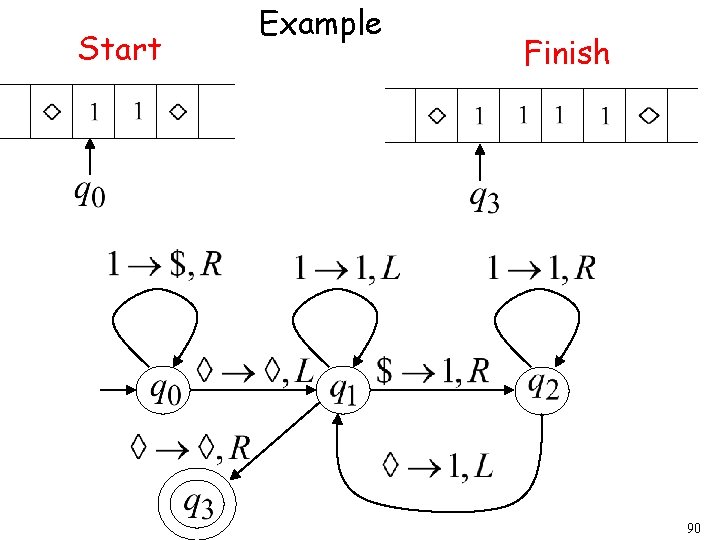
Another Turing Machine Example Turing machine for the language 34

Time 0 35

Time 1 36

Time 2 37

Time 3 38

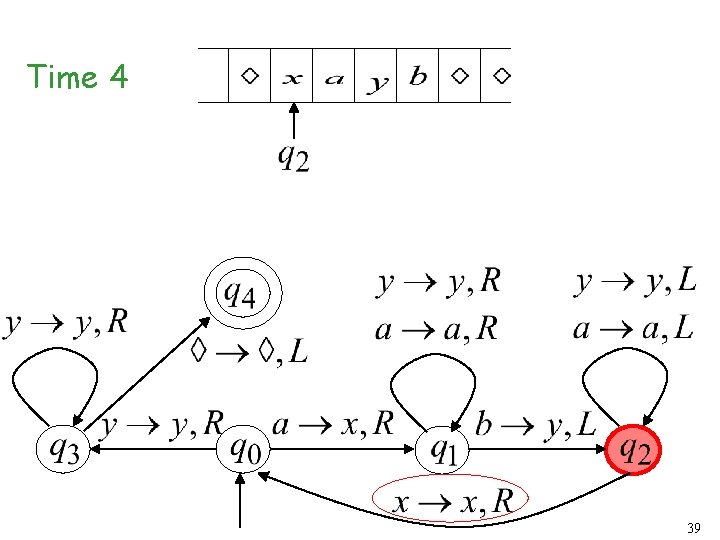
Time 4 39

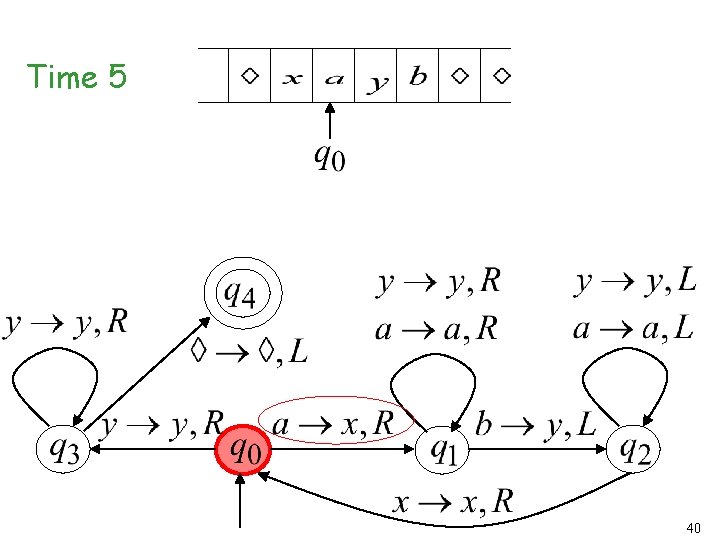
Time 5 40

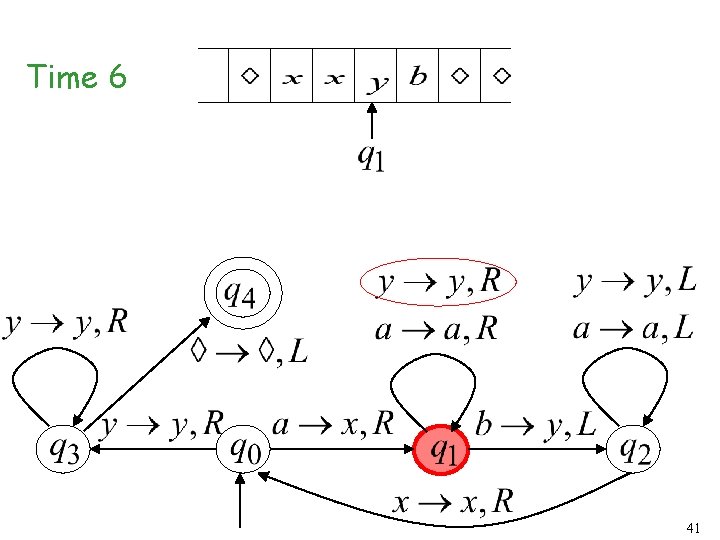
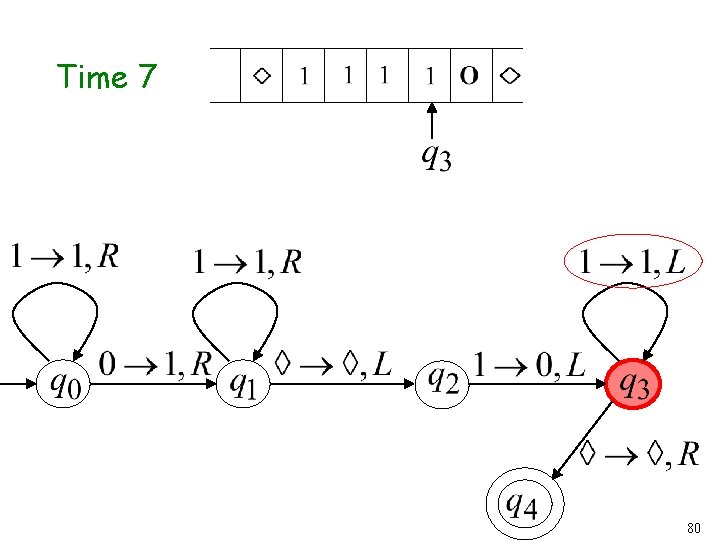
Time 6 41

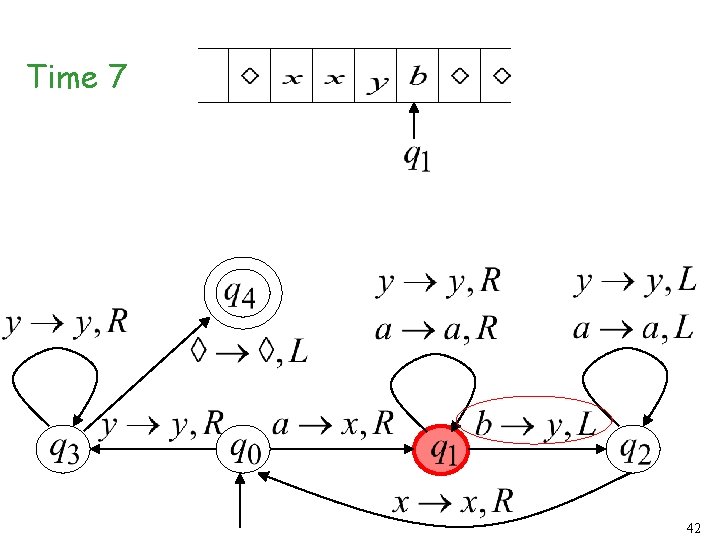
Time 7 42

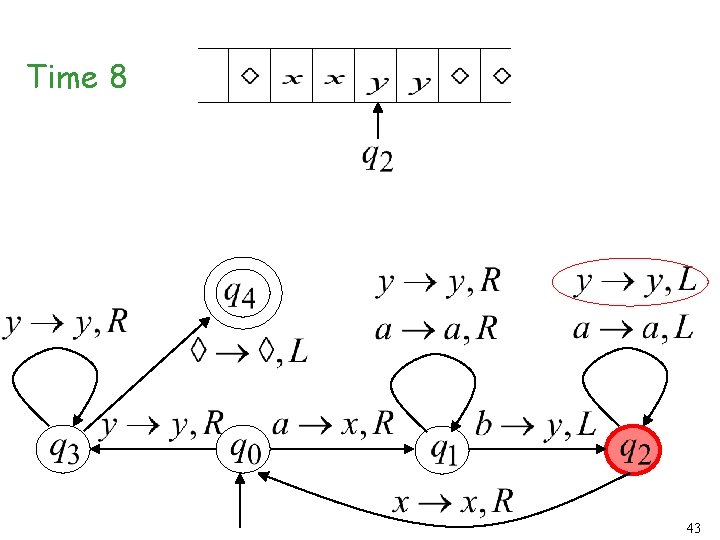
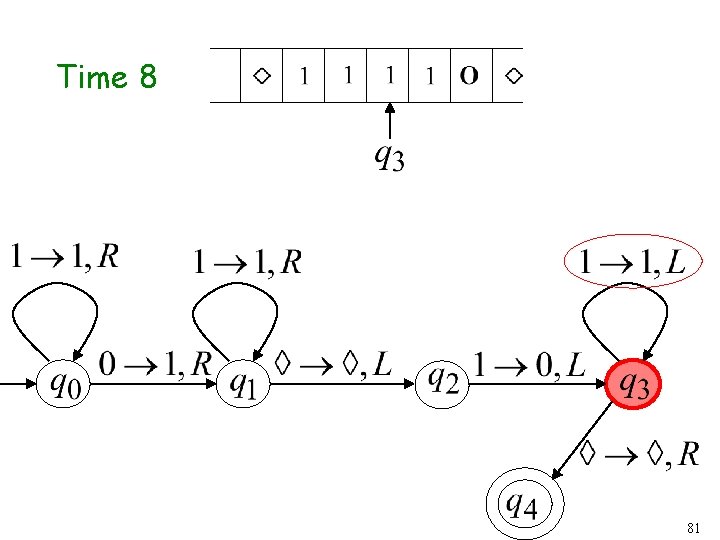
Time 8 43

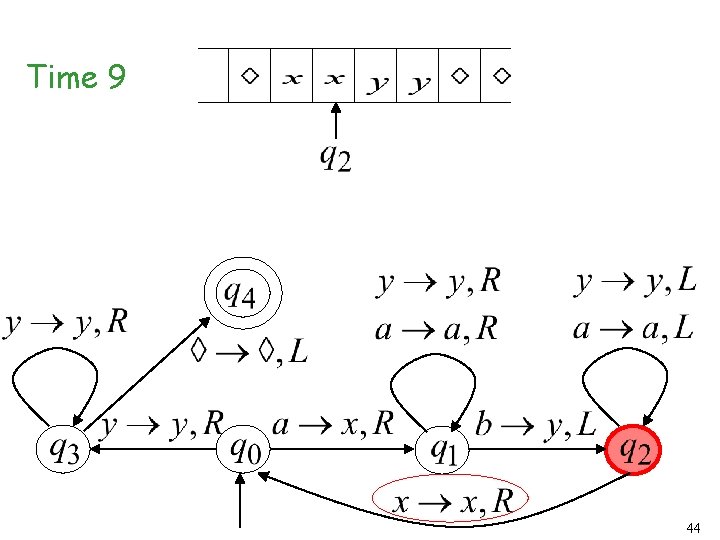
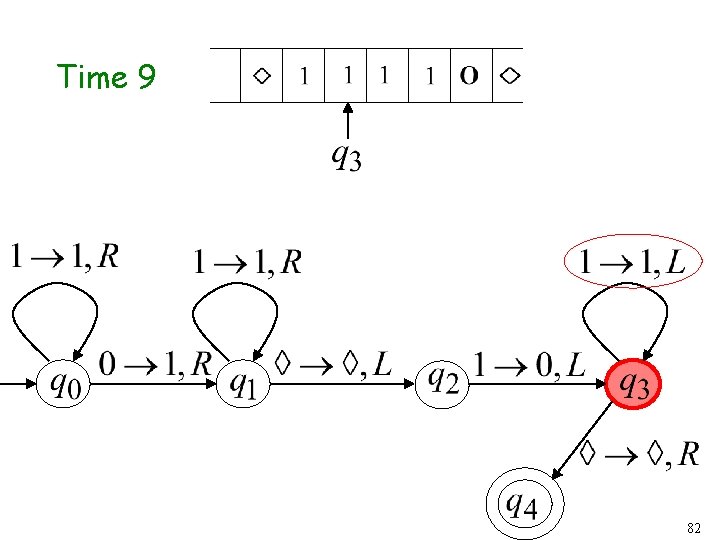
Time 9 44

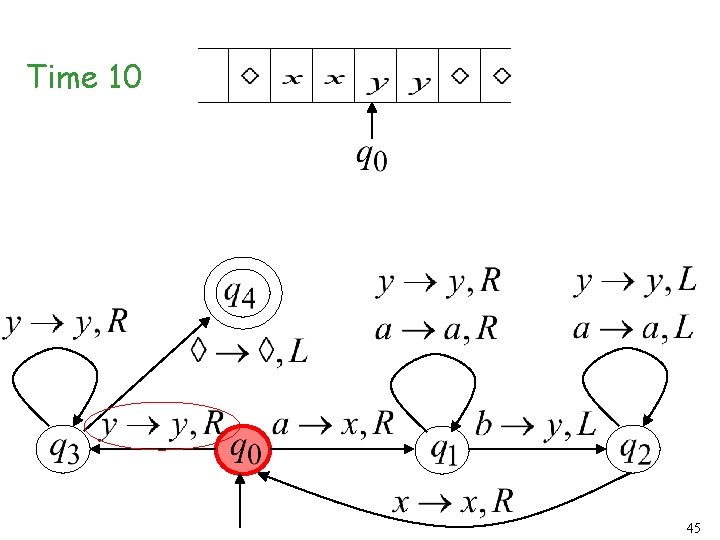
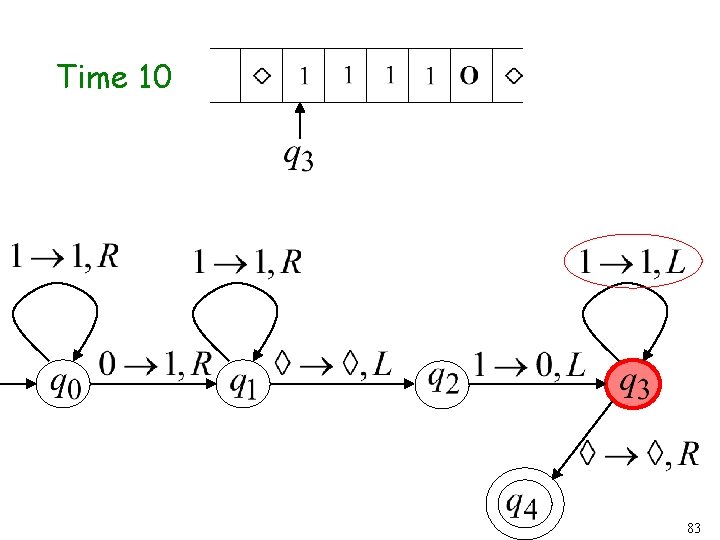
Time 10 45

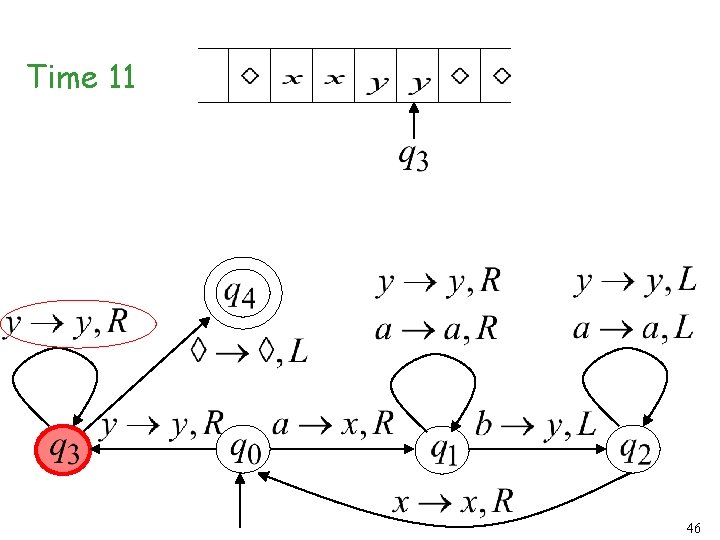
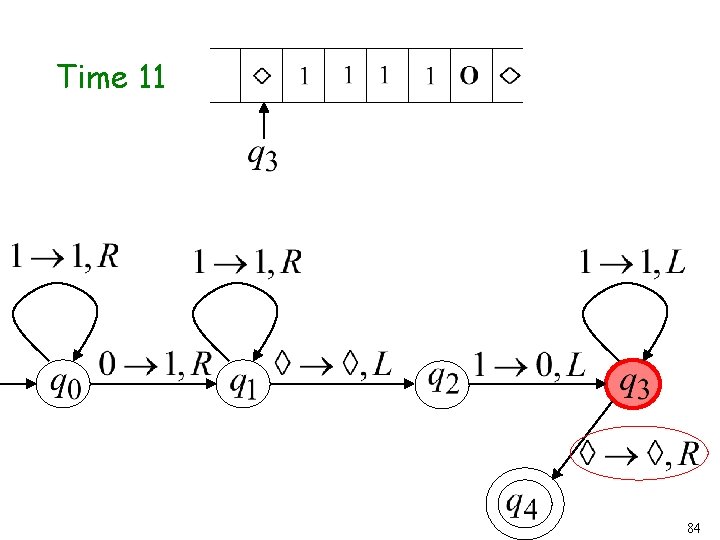
Time 11 46

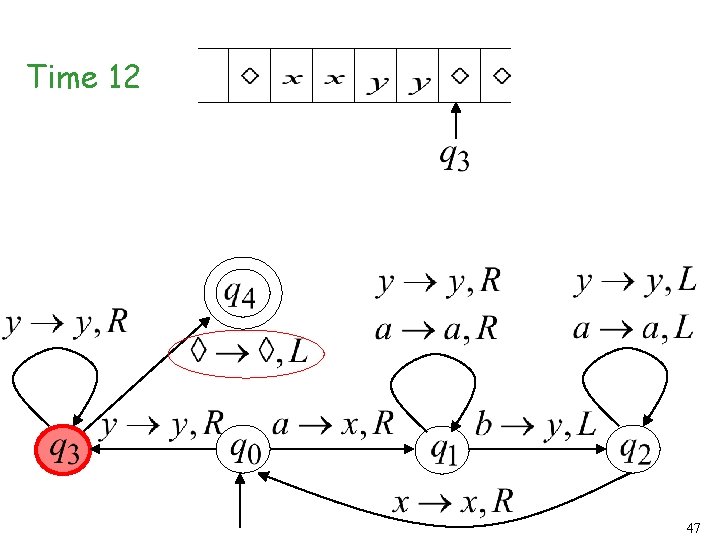
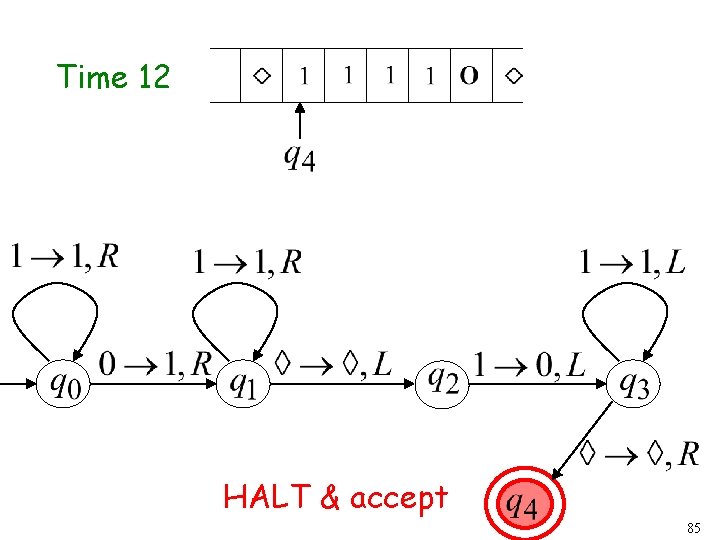
Time 12 47

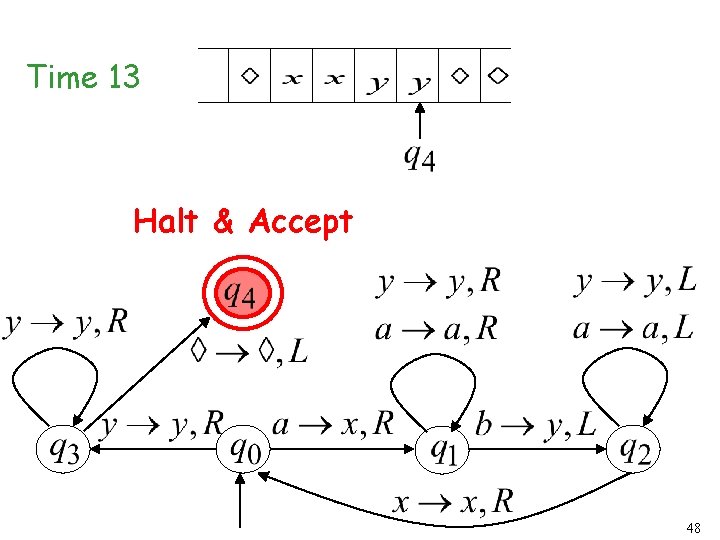
Time 13 Halt & Accept 48

Observation: If we modify the machine for the language we can easily construct a machine for the language 49

Formal Definitions for Turing Machines 50

Transition Function 51

Transition Function 52

Turing Machine: States Input alphabet Tape alphabet Transition function Initial state Final states blank 53

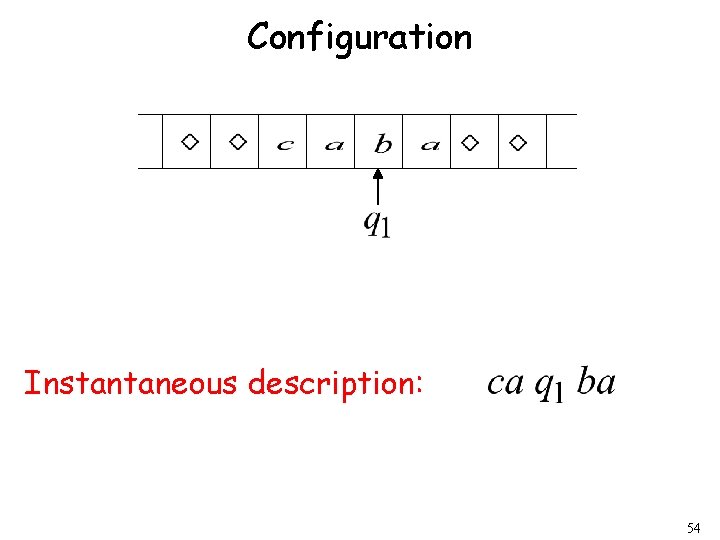
Configuration Instantaneous description: 54

Time 4 Time 5 A Move: 55
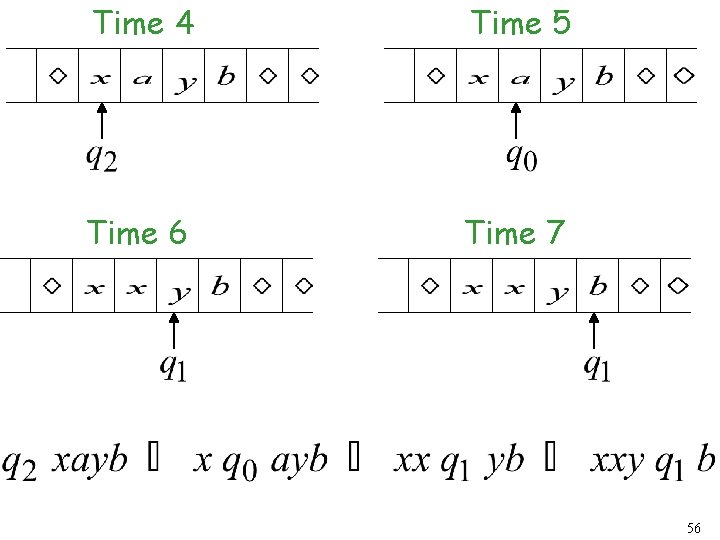
Time 4 Time 5 Time 6 Time 7 56

Equivalent notation: 57

Initial configuration: Input string 58

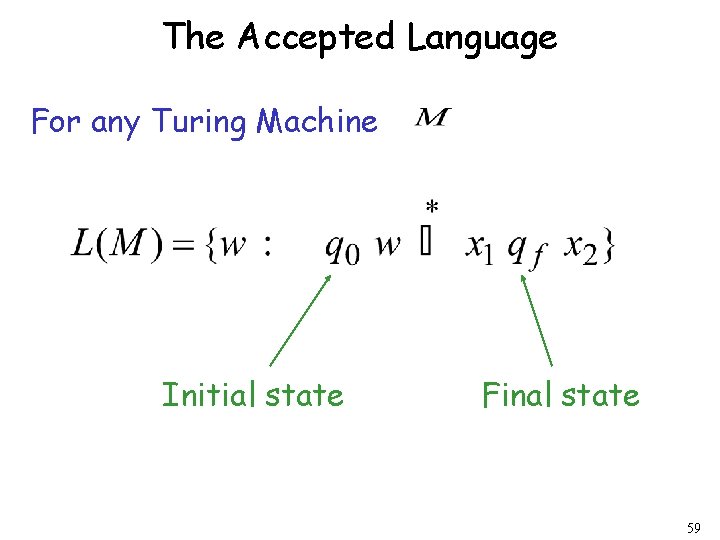
The Accepted Language For any Turing Machine Initial state Final state 59

Standard Turing Machine The machine we described is the standard: • Deterministic • Infinite tape in both directions • Tape is the input/output file 60

Computing Functions with Turing Machines 61

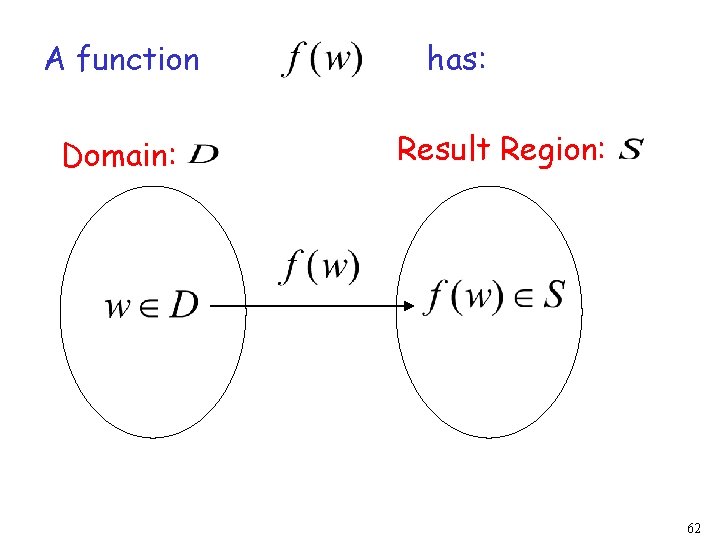
A function Domain: has: Result Region: 62

A function may have many parameters: Example: Addition function 63

Integer Domain Decimal: 5 Binary: 101 Unary: 11111 We prefer unary representation: easier to manipulate with Turing machines 64

Definition: A function is computable if there is a Turing Machine such that: Initial configuration Final configuration initial state For all final state Domain 65

In other words: A function is computable if there is a Turing Machine such that: Initial Configuration For all Final Configuration Domain 66

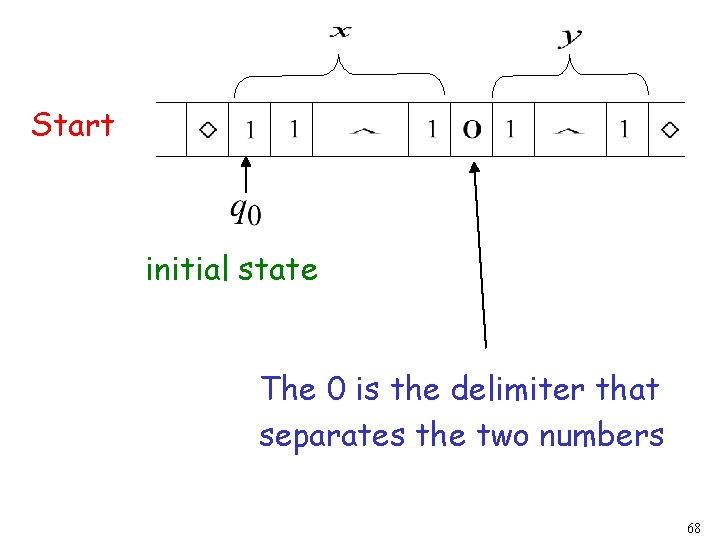
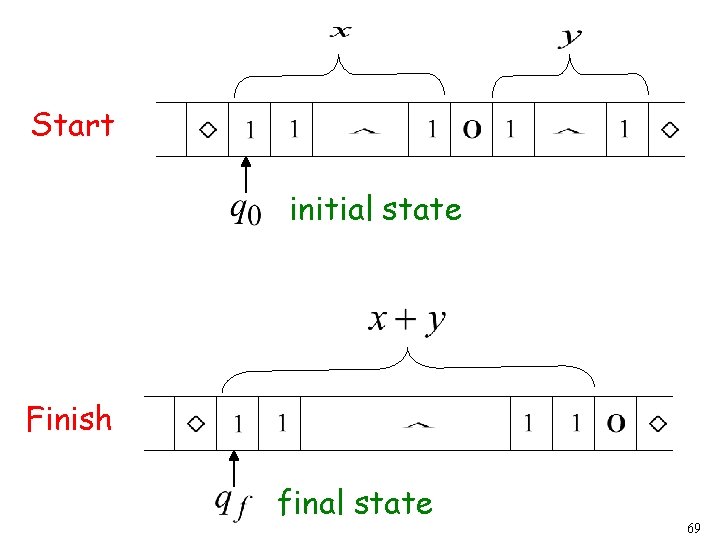
Example The function is computable are integers Turing Machine: Input string: unary Output string: unary 67

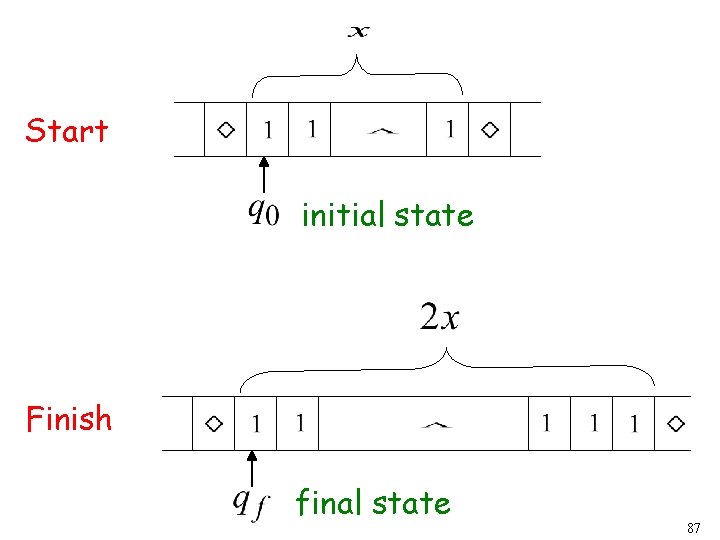
Start initial state The 0 is the delimiter that separates the two numbers 68

Start initial state Finish final state 69

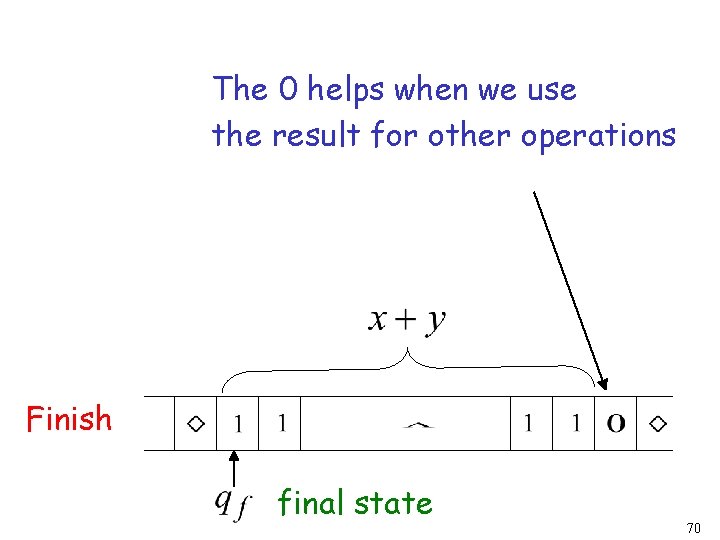
The 0 helps when we use the result for other operations Finish final state 70

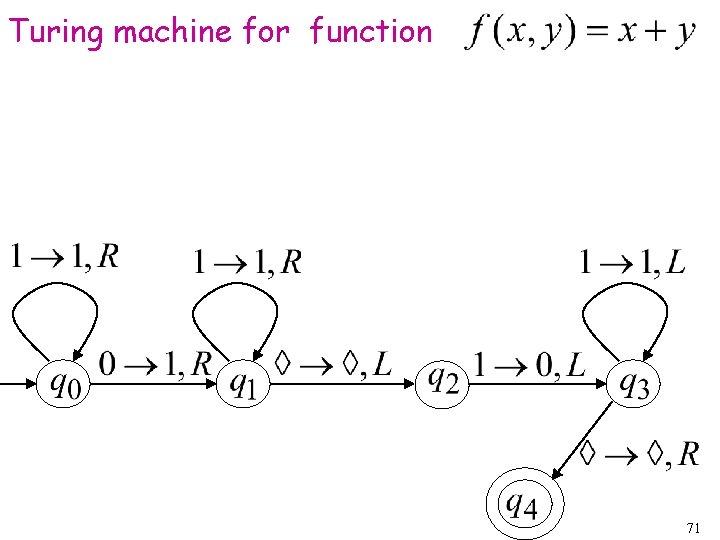
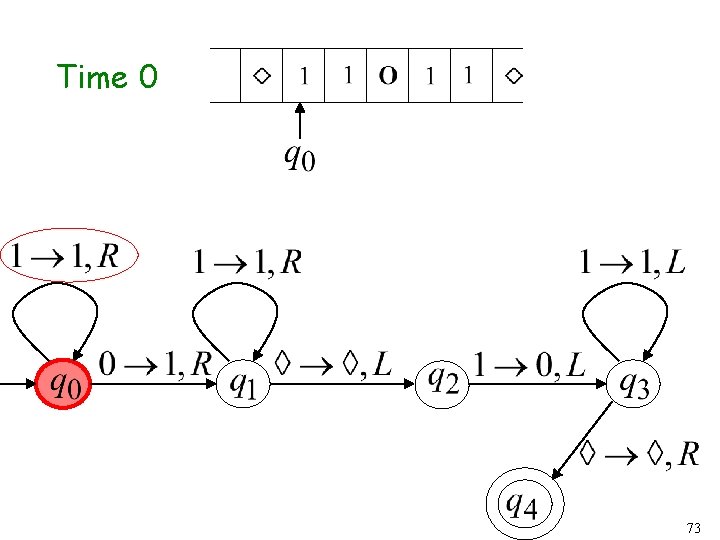
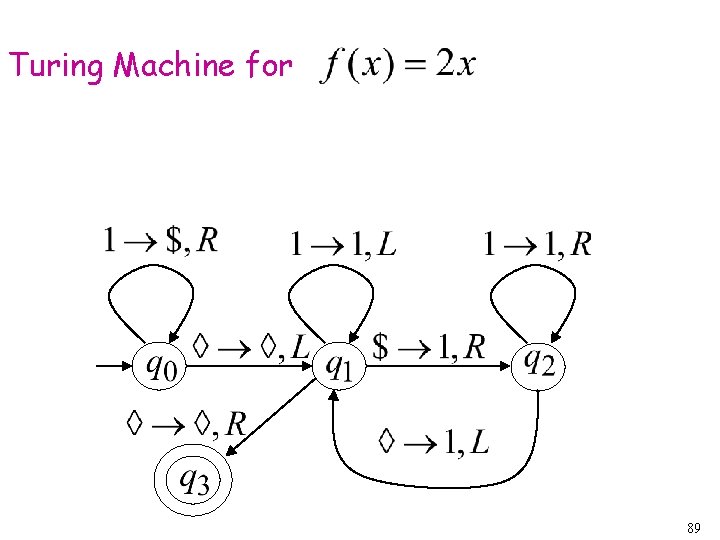
Turing machine for function 71

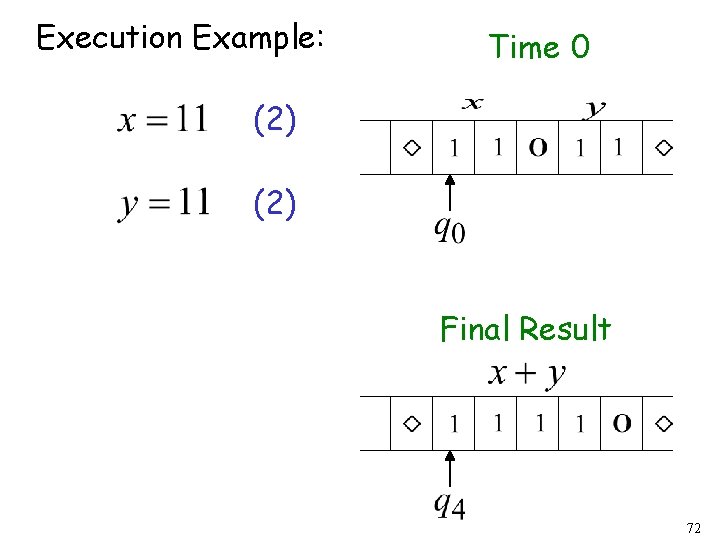
Execution Example: Time 0 (2) Final Result 72

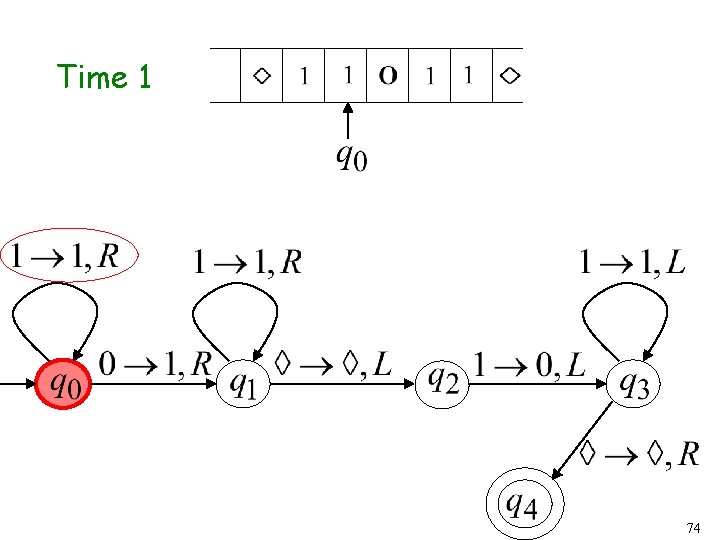
Time 0 73

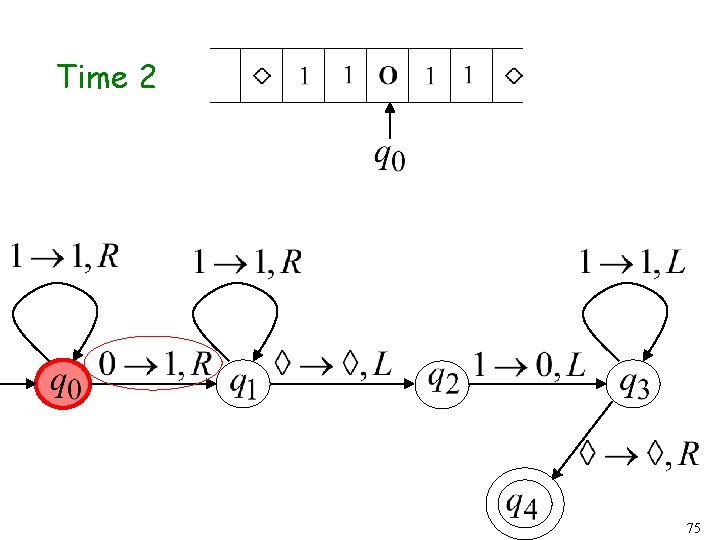
Time 1 74

Time 2 75

Time 3 76

Time 4 77

Time 5 78

Time 6 79

Time 7 80

Time 8 81

Time 9 82

Time 10 83

Time 11 84

Time 12 HALT & accept 85

Another Example The function is computable is integer Turing Machine: Input string: unary Output string: unary 86

Start initial state Finish final state 87

Turing Machine Pseudocode for • Replace every 1 with $ • Repeat: • Find rightmost $, replace it with 1 • Go to right end, insert 1 Until no more $ remain 88

Turing Machine for 89

Start Example Finish 90

Simple TM Examples Turing Machine U+1: Given a string of 1 s on a tape (followed by an infinite number of 0 s), add one more 1 at the end of the string. #11110000……. #111110000………. 91

Simple TM Examples TM: U+1 d(s 0, 1) |-- (s 0, 1, R) d(s 0, 0) |-- (h, 1, STOP) #s 0111100000…. . #1 s 011100000…. . #11 s 01100000…. . #111 s 0100000…. . #1111 s 000000…. . #11111 h 0000…. . STOP 92

Another Example if The function is computable if 93

Turing Machine for if if Input: Output: or 94

Turing Machine Pseudocode: • Repeat Match a 1 from Until all of or with a 1 from is matched • If a 1 from is not matched erase tape, write 1 else erase tape, write 0 95

Combining Turing Machines 96

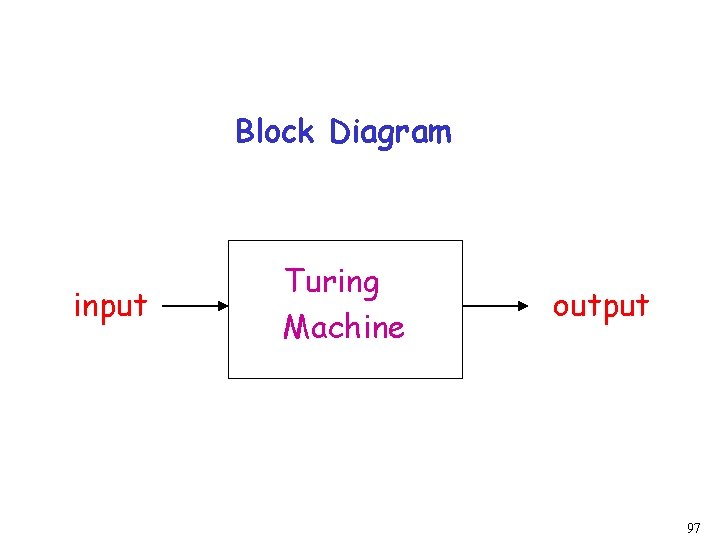
Block Diagram input Turing Machine output 97

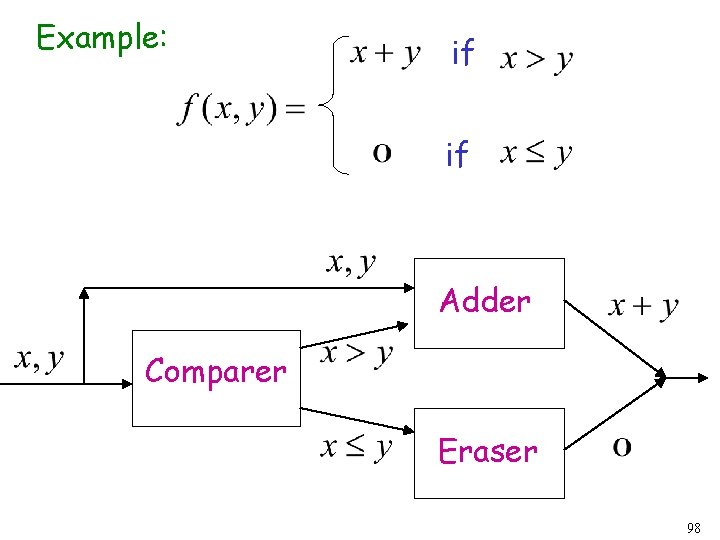
Example: if if Adder Comparer Eraser 98

Turing’s Thesis Any mathematical problem solving that can be described by a mechanical procedure (algorithm) can be modeled by a Turing machine. All computers today perform only mechanical problem solving. They are no more expressive than a Turing machine. 99

Turing’s Thesis Turing’s thesis is not a “theorem” there is no “proof” for thesis. The theorem may be refuted by showing at least one task that is performed by a digital computer which cannot be performed by a Turing machine. Many contentions have been made to this end. However, till date there have not been any conclusive evidence to refute Turing’s thesis. 100

Conclusions TMs are at a level that is much below the assembly language of any typical microprocessor. So in the practical world, TMs are more useful in what they cannot do rather than in what they can. 101

Lab 2 Write some simple. Turing machine programs QUESTIONS? 102