Introduction to Trigonometry Basic Trigonometric Functions What is

Introduction to Trigonometry Basic Trigonometric Functions

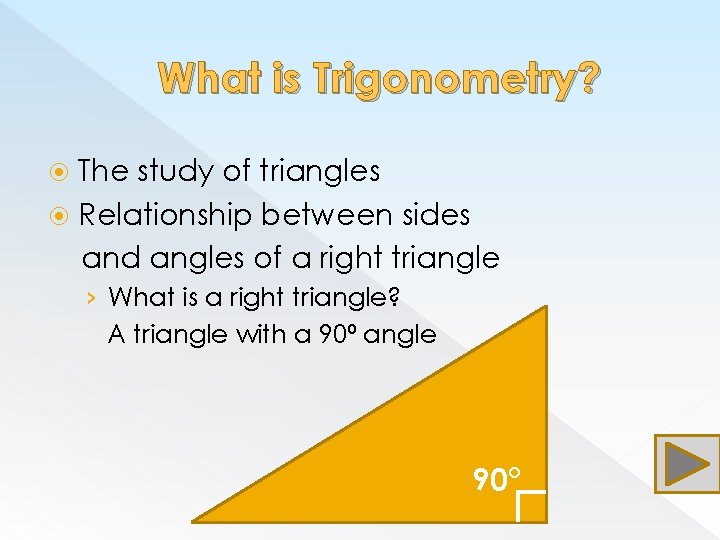
What is Trigonometry? The study of triangles Relationship between sides and angles of a right triangle › What is a right triangle? A triangle with a 90⁰ angle 90°

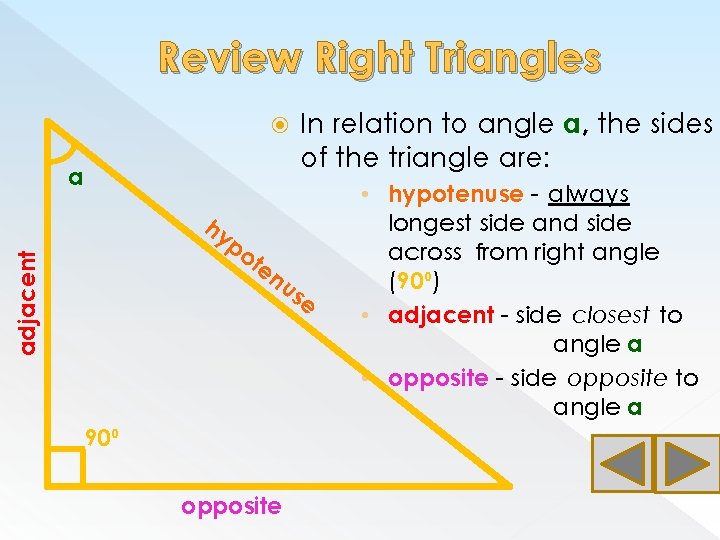
Review Right Triangles a hy adjacent po te nu 90⁰ opposite In relation to angle a, the sides of the triangle are: se • hypotenuse - always longest side and side across from right angle (90⁰) • adjacent - side closest to angle a • opposite - side opposite to angle a

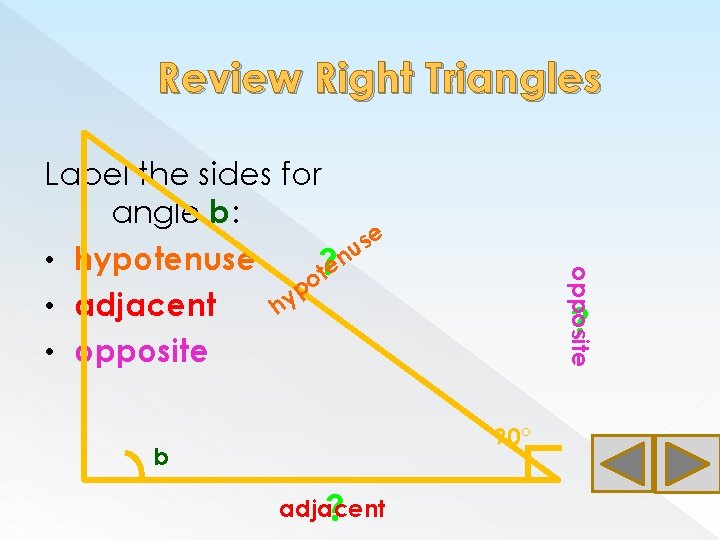
Review Right Triangles opposite Label the sides for angle b: e s u n • hypotenuse ? te o p y • adjacent h • opposite ? 90° b adjacent ?

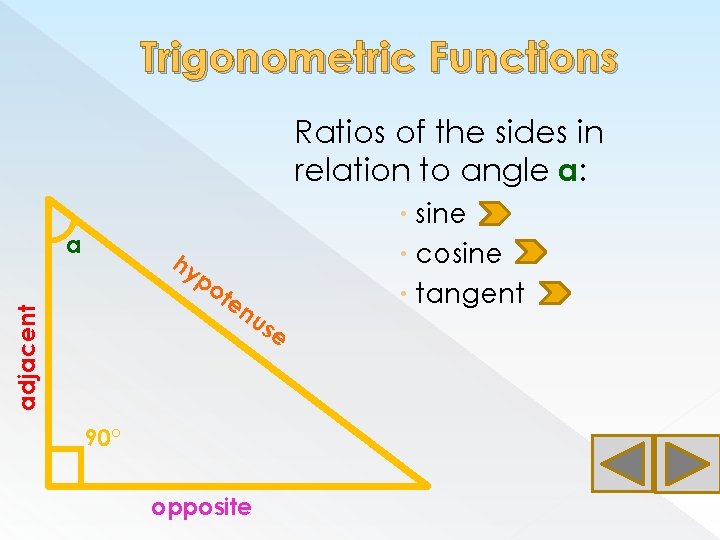
Trigonometric Functions Ratios of the sides in relation to angle a: a hy adjacent po te nu se 90° opposite sine cosine tangent

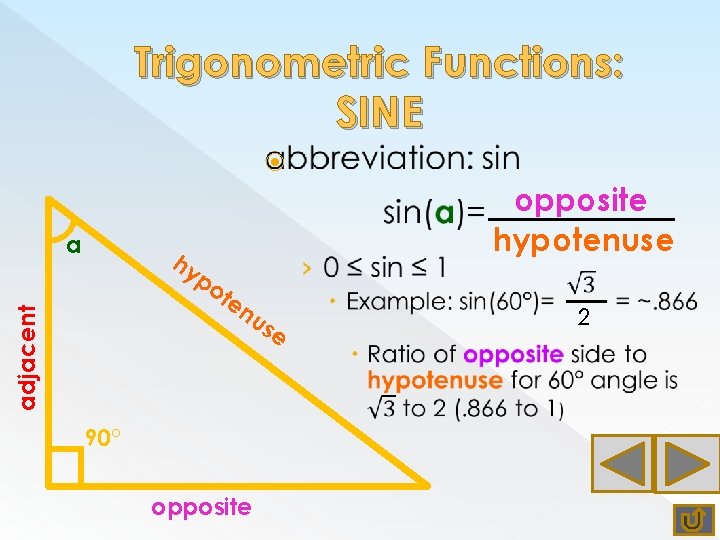
Trigonometric Functions: SINE a opposite hypotenuse hy adjacent po te nu se 90° opposite 2

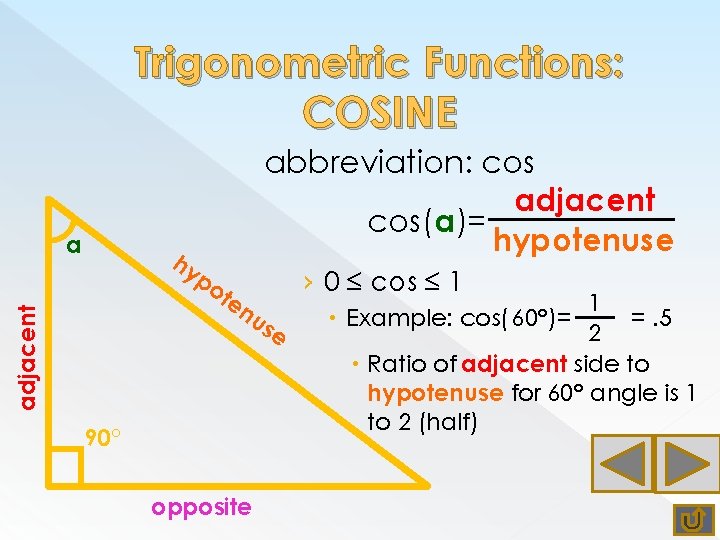
Trigonometric Functions: COSINE a abbreviation: cos adjacent cos(a)= hypotenuse hy adjacent po te nu › 0 ≤ cos ≤ 1 se 90° opposite 1 Example: cos( 60°)= =. 5 2 Ratio of adjacent side to hypotenuse for 60° angle is 1 to 2 (half)

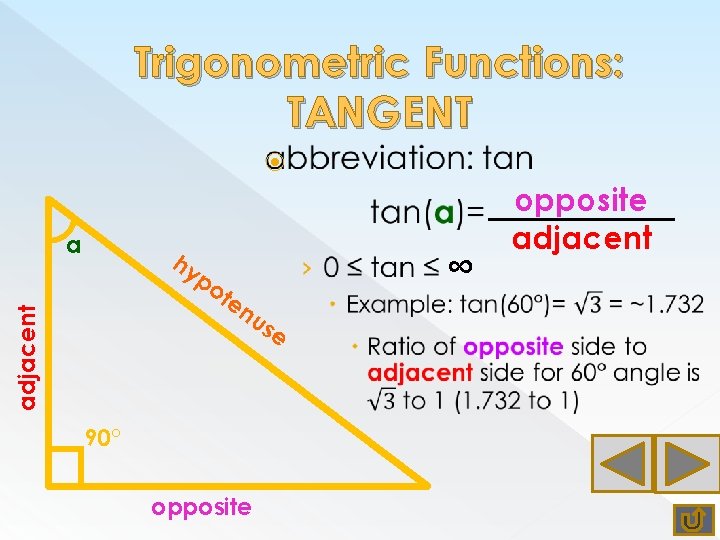
Trigonometric Functions: TANGENT a ∞ hy adjacent po te nu se 90° opposite adjacent

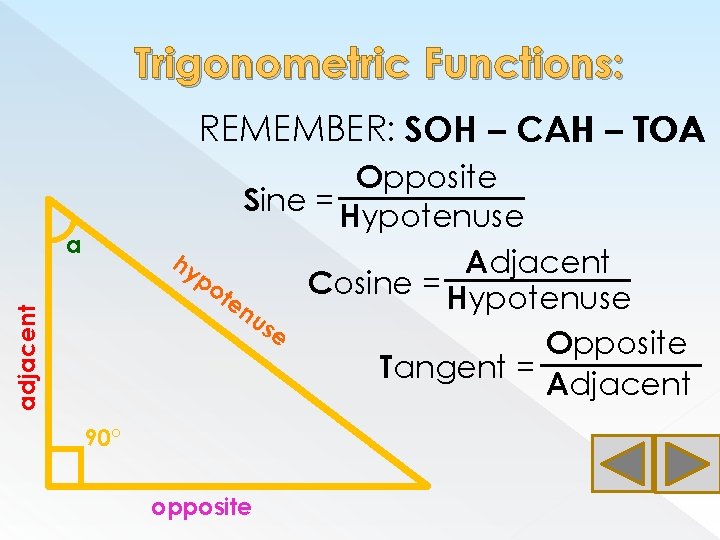
Trigonometric Functions: REMEMBER: SOH – CAH – TOA Opposite Sine = Hypotenuse hy Adjacent po Cosine = Hypotenuse te nu se Opposite Tangent = Adjacent a 90° opposite

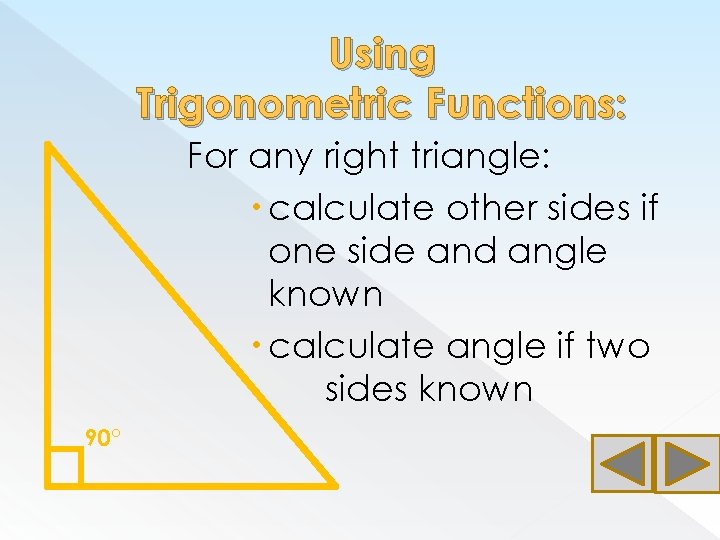
Using Trigonometric Functions: For any right triangle: calculate other sides if one side and angle known calculate angle if two sides known 90°

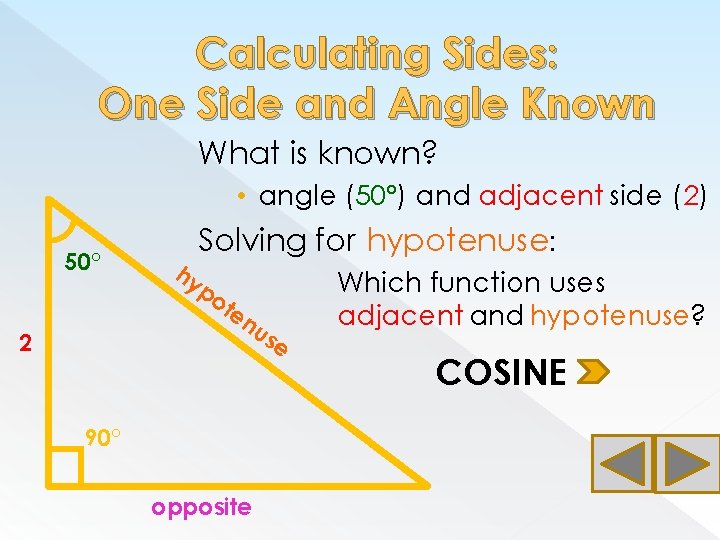
Calculating Sides: One Side and Angle Known What is known? • angle (50°) and adjacent side (2) 50° hy Solving for hypotenuse: po te nu se 2 90° opposite Which function uses adjacent and hypotenuse? COSINE

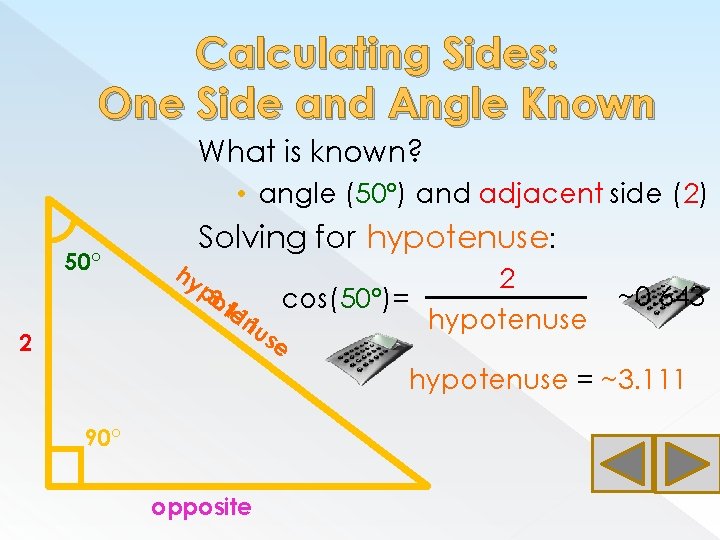
Calculating Sides: One Side and Angle Known What is known? • angle (50°) and adjacent side (2) 50° 2 hy Solving for hypotenuse: 2 p 3 o cos(50°)=. 1 te 1 n 1 u hypotenuse se ~0. 643 = hypotenuse = ~3. 111 90° opposite

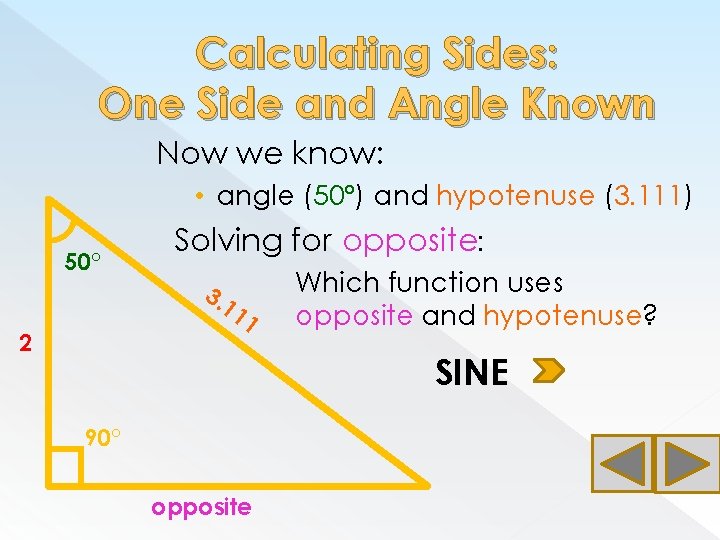
Calculating Sides: One Side and Angle Known Now we know: • angle (50°) and hypotenuse (3. 111) 50° Solving for opposite: 3. 1 11 2 Which function uses opposite and hypotenuse? SINE 90° opposite

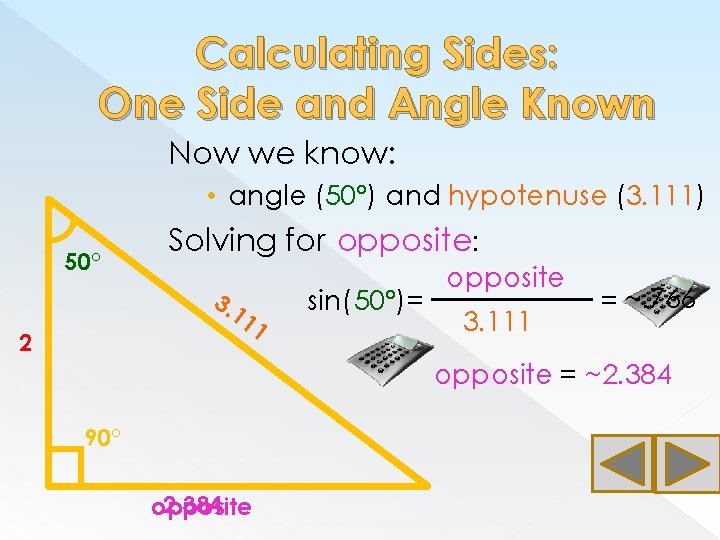
Calculating Sides: One Side and Angle Known Now we know: • angle (50°) and hypotenuse (3. 111) 50° Solving for opposite: 3. 1 11 2 sin(50°)= opposite 3. 111 = ~. 766 opposite = ~2. 384 90° 2. 384 opposite

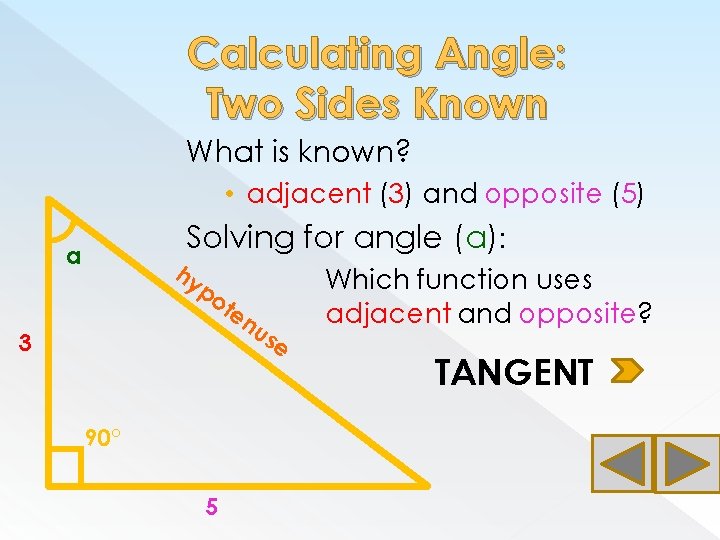
Calculating Angle: Two Sides Known What is known? • adjacent (3) and opposite (5) Solving for angle (a): a hy po te nu se 3 90° 5 Which function uses adjacent and opposite? TANGENT

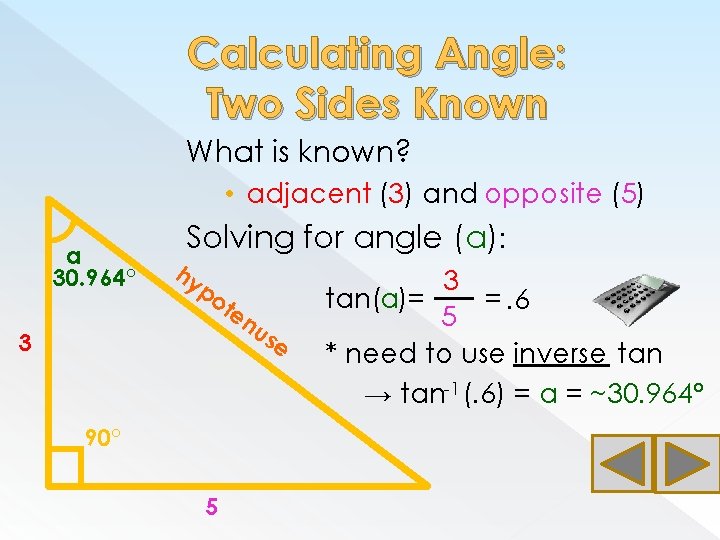
Calculating Angle: Two Sides Known What is known? • adjacent (3) and opposite (5) a 30. 964° Solving for angle (a): hy po te nu se 3 90° 5 3 tan(a)= =. 6 5 * need to use inverse tan → tan-1 (. 6) = a = ~30. 964°