Introduction to Triangulated Graphs Tandy Warnow Topics for

Introduction to Triangulated Graphs Tandy Warnow

Topics for today • Triangulated graphs: theorems and algorithms (Chapters 11. 3 and 11. 9) • Examples of triangulated graphs in phylogeny estimation (Chapters 4. 8, 11. 3 -11. 5)

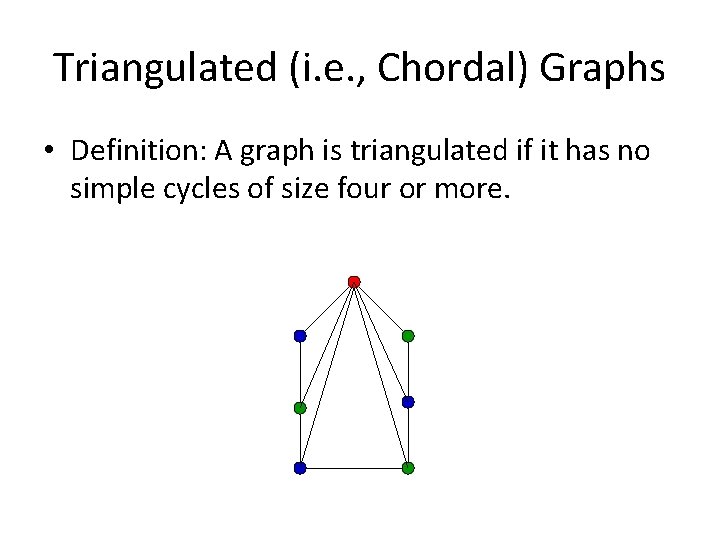
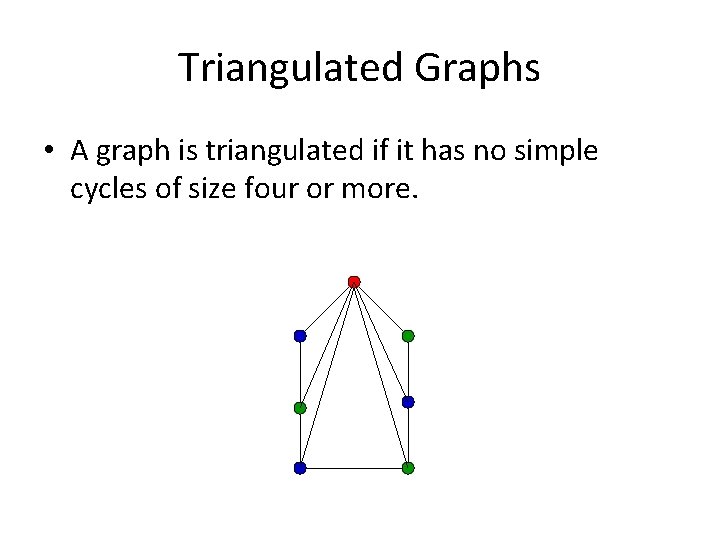
Triangulated (i. e. , Chordal) Graphs • Definition: A graph is triangulated if it has no simple cycles of size four or more.

DCMs are Divide-and-Conquer strategies!

DCMs for phylogeny reconstruction • Define a triangulated graph so that its vertices correspond to the input taxa (or sequences) • Decompose the graph into overlapping subgraphs, thus decomposing the taxa into overlapping subsets. • Apply the “base method” to each subset of taxa, to construct a subset tree • Apply a supertree method to the subset trees to obtain a single tree on the full set of taxa.

DCMs (Disk-Covering Methods) • DCMs for polynomial time methods improve topological accuracy (empirical observation) and have provable theoretical guarantees under Markov models of evolution. • DCMs for hard optimization problems reduce running time needed to achieve good levels of accuracy (empirical observation)

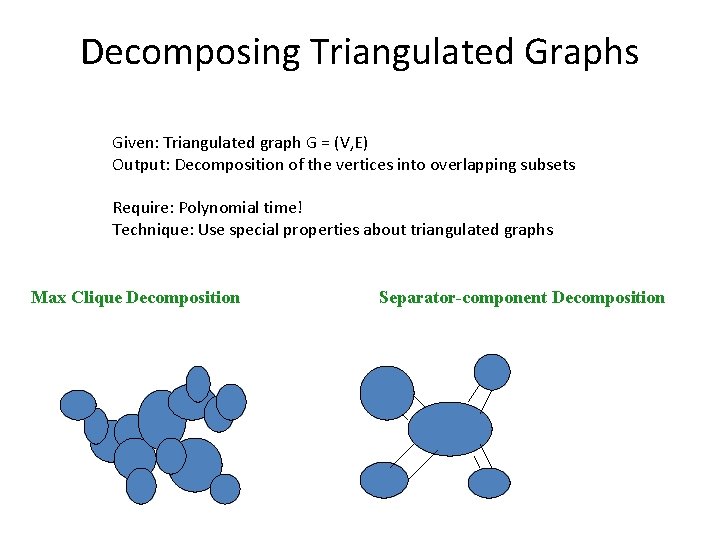
Decomposing Triangulated Graphs Given: Triangulated graph G = (V, E) Output: Decomposition of the vertices into overlapping subsets Require: Polynomial time! Technique: Use special properties about triangulated graphs Max Clique Decomposition Separator-component Decomposition

Simplicial Vertices Definition: Let G=(V, E) be a graph, and let v be a vertex in V. Then v is simplicial if its set of neighbors (i. e. , Γ(v)) is a clique. To do: • Give example of a graph that has no simplicial vertices. • Give example of a graph where every vertex is simplicial.

Perfect Elimination Ordering Definition: Let G=(V, E) be a graph on n vertices. A perfect elimination ordering is an ordering of the vertices v 1, v 2 , …, vn of G so that each vertex vi is simplicial in the graph induced on {vi+1, vi+2 , …, vn}. Theorems: • Every triangulated graph has a simplicial vertex. • In fact, every triangulated graph that is not a clique has two non-adjacent simplicial vertices.

Perfect Elimination Ordering Definition: Let G=(V, E) be a graph on n vertices. A perfect elimination ordering is an ordering of the vertices v 1, v 2 , …, vn of G so that each vertex vi is simplicial in the graph induced on {vi+1, vi+2 , …, vn}. Theorems (Rose 1970): A graph G is triangulated if and only if it has a perfect elimination ordering. Furthermore, given a triangulated graph, a perfect elimination ordering can be found in polynomial time.

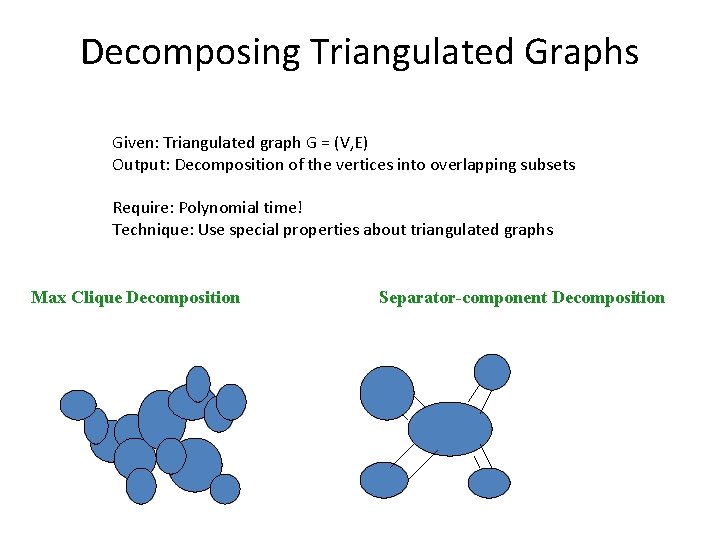
Some properties of chordal graphs • Theorem: Every chordal graph G=(V, E) has at most |V| maximal cliques, and these can be found in polynomial time: – Maxclique decomposition. • Prove this using the existence of a perfect elimination ordering.

Some properties of chordal graphs • Theorem: Every chordal graph G=(V, E) has at most |V| maximal cliques, and these can be found in polynomial time: – Maxclique decomposition. • Prove this using the existence of a perfect elimination ordering.

Some properties of chordal graphs • Every chordal graph that is not a clique has a vertex separator that is a maximal clique, and it can be found in polynomial time: – Separator-component decomposition.

Some properties of chordal graphs • Every chordal graph has at most n maximal cliques, and these can be found in polynomial time: Maxclique decomposition. • Every chordal graph that is not a clique has a vertex separator that is a maximal clique, and it can be found in polynomial time: Separator-component decomposition.

Decomposing Triangulated Graphs Given: Triangulated graph G = (V, E) Output: Decomposition of the vertices into overlapping subsets Require: Polynomial time! Technique: Use special properties about triangulated graphs Max Clique Decomposition Separator-component Decomposition

DCMs are Divide-and-Conquer strategies!

How to combine subset trees? • Every triangulated graph has a perfect elimination ordering: – enables us to merge correct subtrees and get a correct supertree back, if subtrees are big enough (so that they contain all the short quartet trees).

Triangulated Graphs and Trees Theorem (Gravil 1974, Buneman 1974): A graph G is triangulated if and only if G is the intersection graph of a set of subtrees of a tree. Proof: One direction is easy, and the other is not…

Examples of Triangulated Graphs • Threshold graphs TG(D, q): D is additive and q is any real number, and (x, y) is an edge if and only if D[x, y] <= q. • Short Subtree Graphs SSG(T, w): T is a tree with edge-weighting w, and every short quartet contributes a 4 -clique. • Character-state intersection graphs from perfect phylogenies.

Examples of Triangulated Graphs • Threshold graphs TG(D, q): D is additive and q is any real number, and (x, y) is an edge if and only if D[x, y] <= q. • Theorem: For all additive matrices D and thresholds q, TG(D, q) is triangulated. • Proof: Use the fact that all subtree intersection graphs are triangulated.

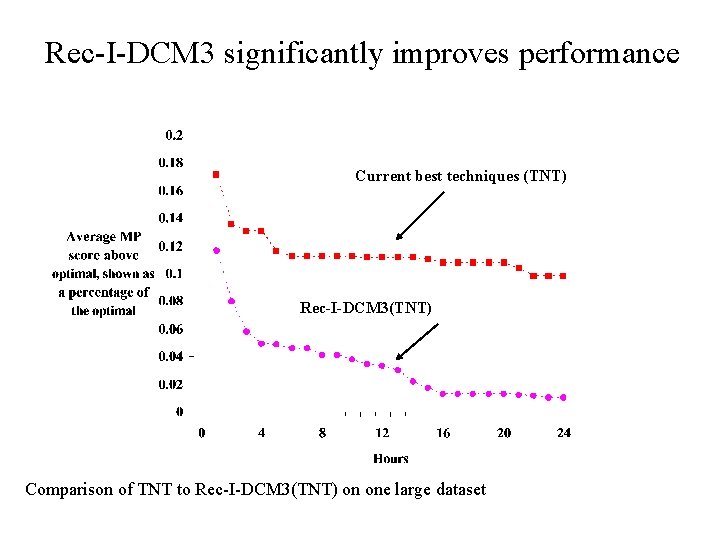
DCM 1 -boosting distance-based methods [Nakhleh et al. ISMB 2001] Error Rate 0. 8 NJ DCM 1 -NJ 0. 6 0. 4 • Theorem (Warnow et al. , SODA 2001): DCM 1 -NJ converges to the true tree from polynomial length sequences 0. 2 0 0 400 800 No. Taxa 1200 1600

Examples of Triangulated Graphs • Short Subtree Graphs SSG(T, w): T is a tree with edge-weighting w, and every short quartet contributes a 4 -clique. • Theorem: For all trees T with edge weighting w, SSG(T, w) is additive. • Proof: Use the fact that all subtree intersection graphs are triangulated.

Rec-I-DCM 3 significantly improves performance Current best techniques (TNT) Rec-I-DCM 3(TNT) Comparison of TNT to Rec-I-DCM 3(TNT) on one large dataset

Examples of Triangulated Graphs • Character-state intersection graphs from perfect phylogenies. • Theorem: For all perfect phylogenies, the character state intersection graph (where nodes correspond to character states and edges correspond to any two states at any node in the tree – internal and leaf) is triangulated. • Proof: Use the fact that all subtree intersection graphs are triangulated.

“Homoplasy-Free” Evolution (perfect phylogenies) YES NO

Perfect Phylogeny • A phylogeny T for a set S of taxa is a perfect phylogeny if each state of each character occupies a subtree (no character has backmutations or parallel evolution) 30

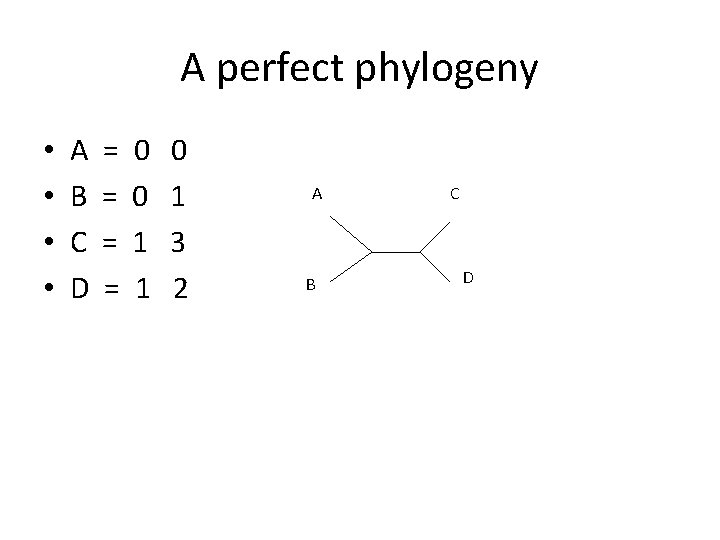
Perfect phylogenies, cont. • A=(0, 0), B=(0, 1), C=(1, 3), D=(1, 2) has a perfect phylogeny! • A=(0, 0), B=(0, 1), C=(1, 0), D=(1, 1) does not have a perfect phylogeny!

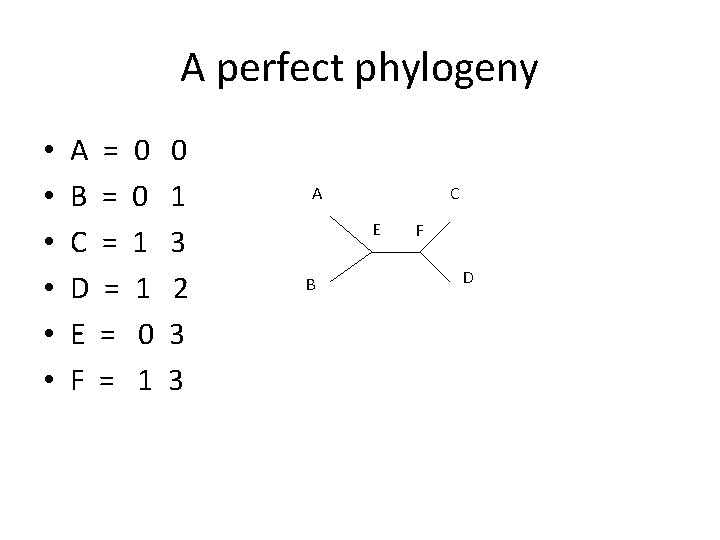
A perfect phylogeny • • • A = B = C = D = E = F = 0 0 1 1 0 1 3 2 3 3 A B C D

A perfect phylogeny • • • A = B = C = D = E = F = 0 0 1 1 0 1 3 2 3 3 A C E B F D

The Perfect Phylogeny Problem • Given a set S of taxa (species, languages, etc. ) determine if a perfect phylogeny T exists for S. • The problem of determining whether a perfect phylogeny exists is NP-hard (Mc. Morris et al. 1994, Steel 1991).

Triangulated Graphs • A graph is triangulated if it has no simple cycles of size four or more.

Triangulated Graphs Theorem (Gravil 1974, Buneman 1974): A graph G is triangulated if and only if G is the intersection graph of a set of subtrees of a tree. Proof: One direction is easy, and the other is not…

Perfect Phylogenies and Triangulated Colored Graphs • Suppose M is a character matrix and T is a perfect phylogeny for M. • Then let M’ be the extension of M to include the additional “species” added at the internal nodes. • Character State Intersection Graph G based on M’: – For each character alpha and state i in M’, give a vertex v(alpha, i) and color the vertex with the color for alpha. – Put edges between two vertices if they share any species. – G is triangulated and properly colored.

Perfect Phylogenies and Triangulated Colored Graphs • Suppose M is a character matrix and T is a perfect phylogeny for M. • Then let M’ be the extension of M to include the additional “species” added at the internal nodes. • The character state intersection graph G based on M’ is triangulated and properly colored. (Why? ) • But if we had based it on M it might not have been triangulated. (Why? )

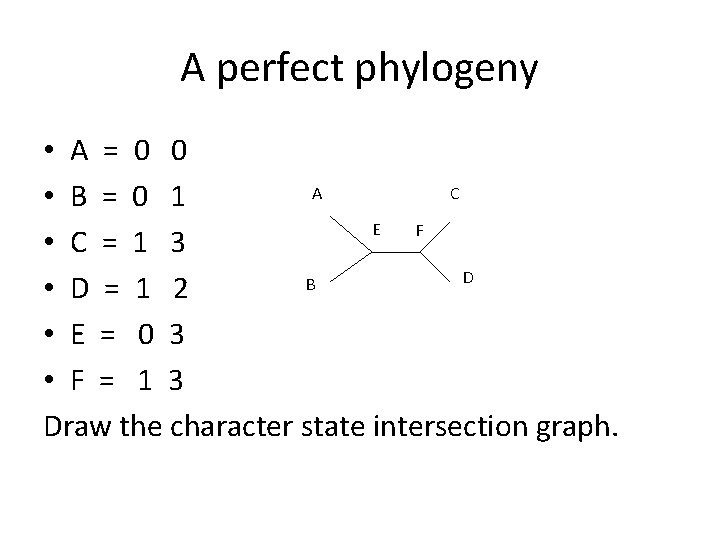
A perfect phylogeny • A = 0 0 A C • B = 0 1 E F • C = 1 3 D B • D = 1 2 • E = 0 3 • F = 1 3 Draw the character state intersection graph.

Matrix with a perfect phylogeny c 1 s 1 3 s 2 1 s 3 1 s 4 2 c 3 2 1 2 2 1 3 1 1 Draw the perfect phylogeny and compute the sequences at the internal nodes.

Matrix with a perfect phylogeny c 1 s 1 3 s 2 1 s 3 1 s 4 2 c 3 2 1 2 2 1 3 1 1 Draw the character state intersection graph for the extended matrix (including the sequences at the internal nodes).

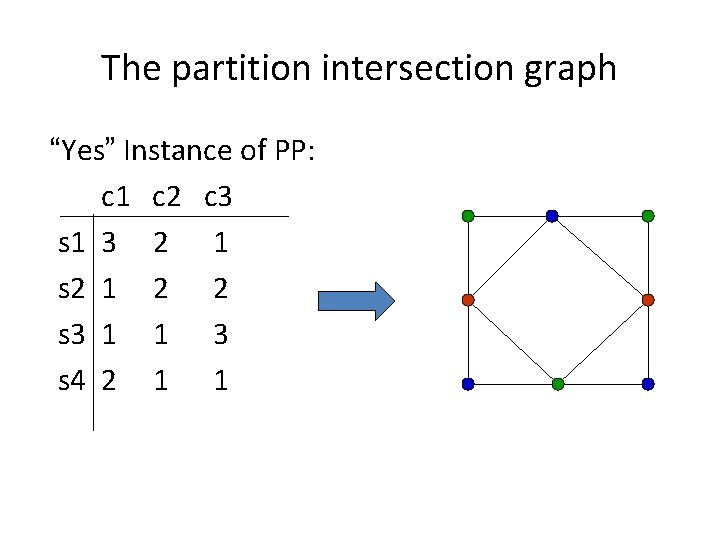
The partition intersection graph “Yes” Instance of PP: c 1 c 2 c 3 s 1 3 2 1 s 2 1 2 2 s 3 1 1 3 s 4 2 1 1

Triangulating colored graphs • Let G=(V, E) be a graph and c be a vertex coloring of G. Then G can be c-triangulated if a supergraph G’=(V, E’) exists that is triangulated and where the coloring c is proper. • In other words, G can be c-triangulated if and only if we can add edges to G to make it triangulated without adding edges between vertices of the same color.

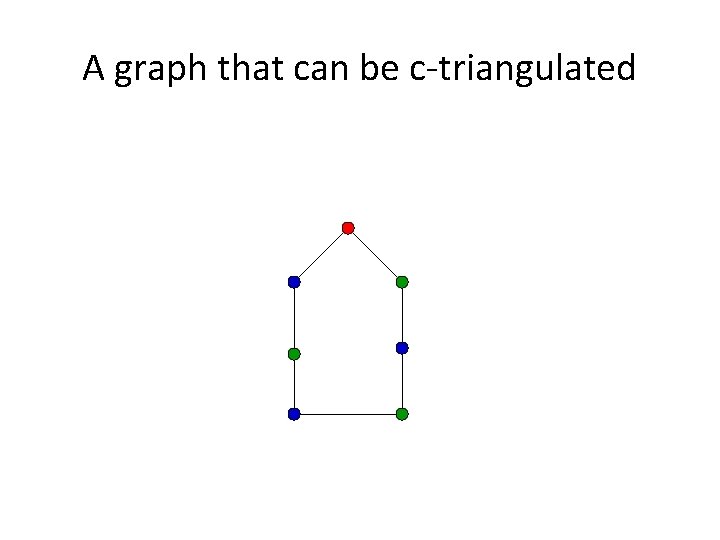
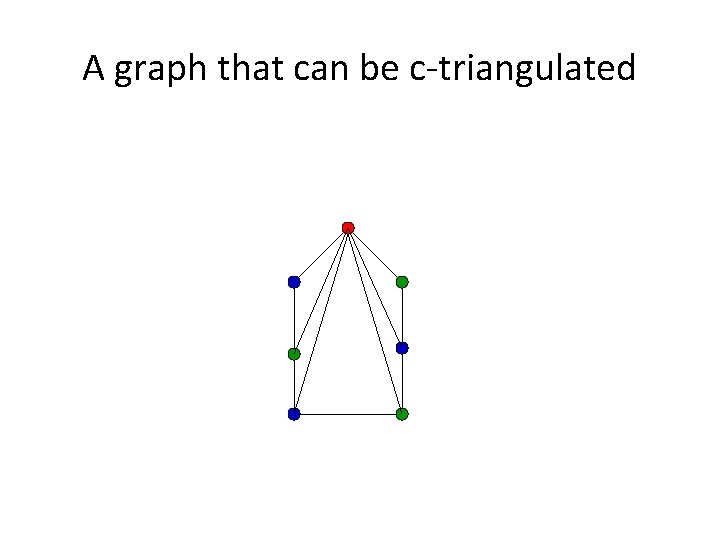
A graph that can be c-triangulated

A graph that can be c-triangulated

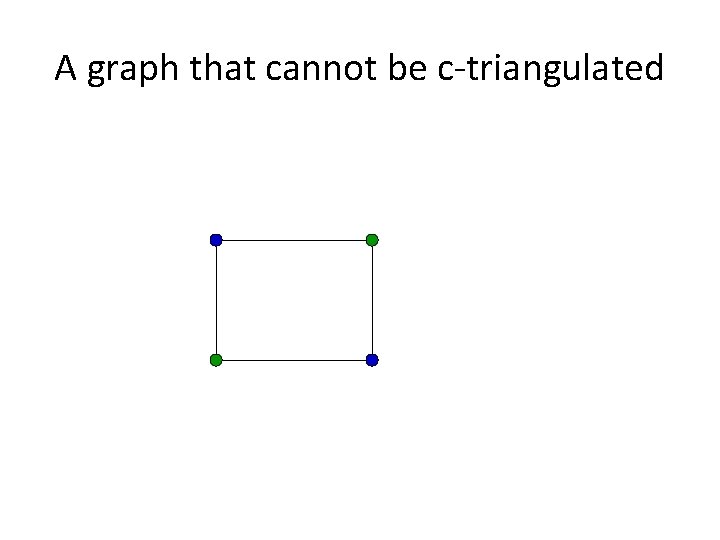
A graph that cannot be c-triangulated

Triangulating Colored Graphs (TCG) Triangulating Colored Graphs: given a vertexcolored graph G, determine if G can be ctriangulated.

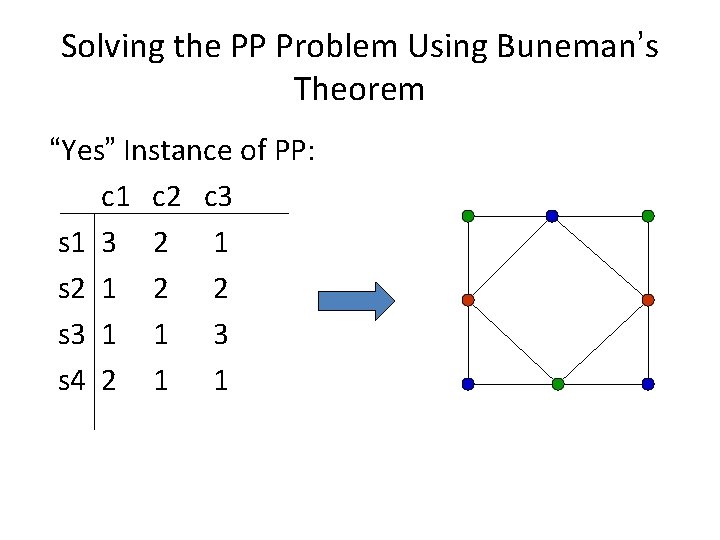
The PP and TCG Problems • Buneman’s Theorem: A perfect phylogeny exists for a set S if and only if the associated character state intersection graph can be ctriangulated. • The PP and TCG problems are polynomially equivalent and NP-hard.

A no-instance of Perfect Phylogeny • • A B C D =00 =01 =10 =11 0 1 An input to perfect phylogeny (left) of four sequences described by two characters, and its character state intersection graph. Note that the character state intersection graph is 2 -colored.

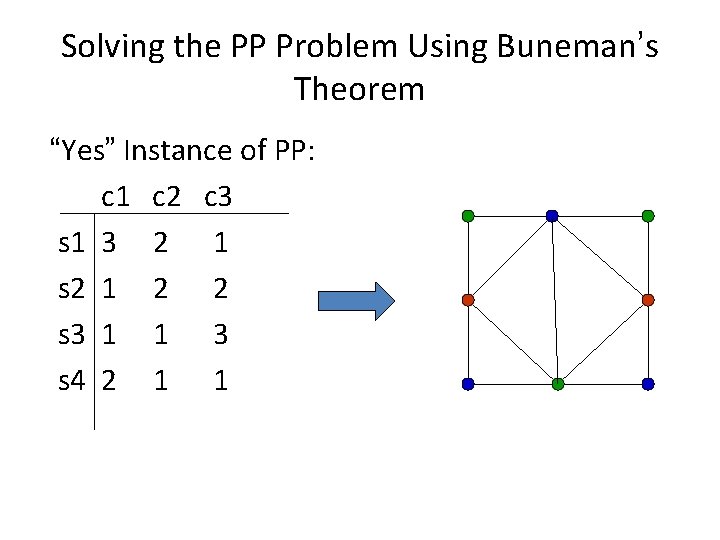
Solving the PP Problem Using Buneman’s Theorem “Yes” Instance of PP: c 1 c 2 c 3 s 1 3 2 1 s 2 1 2 2 s 3 1 1 3 s 4 2 1 1

Solving the PP Problem Using Buneman’s Theorem “Yes” Instance of PP: c 1 c 2 c 3 s 1 3 2 1 s 2 1 2 2 s 3 1 1 3 s 4 2 1 1

Some special cases are easy • Binary character perfect phylogeny solvable in linear time • r-state characters solvable in polynomial time for each r (combinatorial algorithm) • Two character perfect phylogeny solvable in polynomial time (produces 2 -colored graph) • k-character perfect phylogeny solvable in polynomial time for each k (produces k-colored graphs -connections to Robertson-Seymour graph minor theory)

Early History • • Le. Quesne (1969, 1972, 1974, 1977): initial formulation of perfect phylogenies Estabrook (1972), Estabrook et al. (1975): mathematical foundations of perfect phylogenies Mc. Morris (1997): binary character compatibility Felsenstein (1984): review paper Estabrook & Landrum, Fitch 1975: compatibility of two characters Steel (1992) and Bodlaender et al. (1992): NP-hardness Buneman (1974): reduced perfect phylogeny to triangulating colored graphs Kannan and Warnow (1992): established equivalence of TCG and PP See T. Warnow, 1993. Constructing phylogenetic trees efficiently using compatibility criteria. New Zealand Journal of Botany, 31: 3, pp. 239 -248 (linked off my homepage) for a survey of the early literature and the full citations.

Literature sample • • • R. Agarwala and D. Fernandez-Baca, 1994. A polynomial-time algorithm for the perfect phylogeny problem when the number of character states is fixed. SIAM Journal on Computing, 23 , 1216– 1224. R. Agarwala and D. Fernandez-Baca, 1996. Simple algorithms for perfect phylogeny and triangulating colored graphs. International Journal of Foundations of Computer Science, 7 , 11– 21. H. L. Bodlaender, M. R. Fellows, Michael T. Hallett, H. Todd Wareham, and T. Warnow. 2000. The hardness of perfect phylogeny, feasible register assignment and other problems on thin colored graphs, Theoretical Computer Science 244 (2000) 167 -188 H. L. Bodlaender and T. KIoks, 1993: A simple linear time algorithm for triangulating three-colored graphs. Journal of algorithms J 5: 160 -172. D. Fernandez-Baca, 2000. The perfect phylogeny problem. Pages 203– 234 of: Du, D. -Z. , and Cheng, X. (eds), Steiner Trees in Industries. Kluwer Academic Publishers. D. Gusfield, 1991. Efficient algorithms for inferring evolutionary trees. Networks 21, 19– 28. R. Idury and A. Schaffer. 1993: Triangulating three-colored graphs in linear time and linear space. SIAM journal on discrete mathematics 6: 289 -294. S. Kannan and T. Warnow, 1992. Triangulating 3 -colored graphs. SIAM J. on Discrete Mathematics, Vol. 5 No. 2, pp. 249 -258 (also SODA 1991) S. Kannan and T. Warnow, 1997. A fast algorithm for the computation and enumeration of perfect phylogenies when the number of character states is fixed. SIAM J. Computing, Vol. 26, No. 6, pp. 1749 -1763 (also SODA 1995) F. R. Mc. Morris, T. Warnow, and T. Wimer, 1994. Triangulating Vertex Colored Graphs. SIAM J. on Discrete Mathematics, Vol. 7, No. 2, pp. 296 -306 (also SODA 1993).

Applications of Perfect Phylogeny • Tumor Phylogenetics (Mohammed El-Kebir will talk this on April 10 -17, 2018) • Historical Linguistics (I will talk about this on March 15, 2018) • Population genetics and Haplotype inference