Introduction to Trees Tree example Consider this program

Introduction to Trees

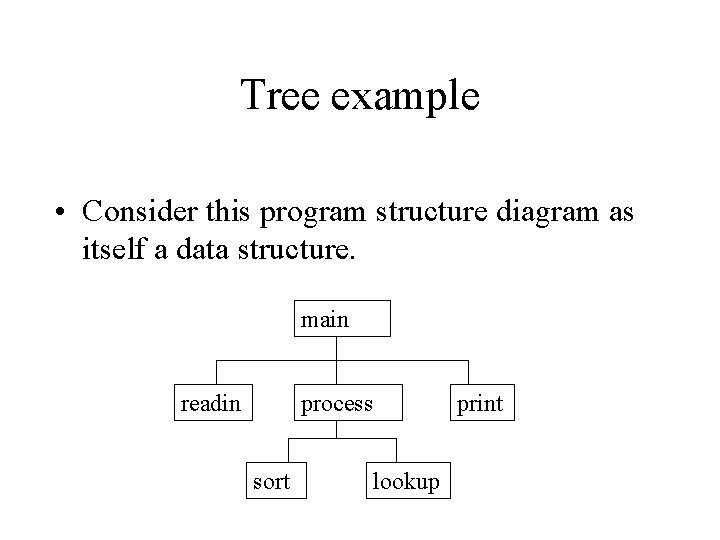
Tree example • Consider this program structure diagram as itself a data structure. main readin process sort print lookup

Terminology • Node - an element of a tree • Root node - the single node at level 0 • Child node - nodes at level 1 or lower (descending from a parent node). Note: a node can have only one parent.

Terminology (continued) • Parent node - a node at one level associated with nodes at a lower level (children). • Note: nodes without children are called leaves. • Every node of a tree is the root of a subtree.

• As you can see by the diagram of a tree, its structure is highly recursive. Therefore, as you would expect, the procedures and functions that manipulate trees are also recursive in nature.

The tree as an ADT • Fundamental operations Create(Root) Empty(Root) Find(Root, Target. Loc) Add(Root, Node) Delete(Root, Node) Traverse(Root)

Binary Trees • This (next slide) is an example of a binary tree (ie. one in which each node has no more than two children)

Binary tree example

(see previous tree) • This tree also has the property that each node is greater than either of its children. Another name for it is a heap (not to be confused with the system heap).

Question: • What is the hierarchical ordering principal for this tree? • (see next slide)

What is the ordering property?

Answer: • Each node is greater than all of the nodes in its left subtree and less than all of the nodes in its right subtree. • This is called its ordering property.

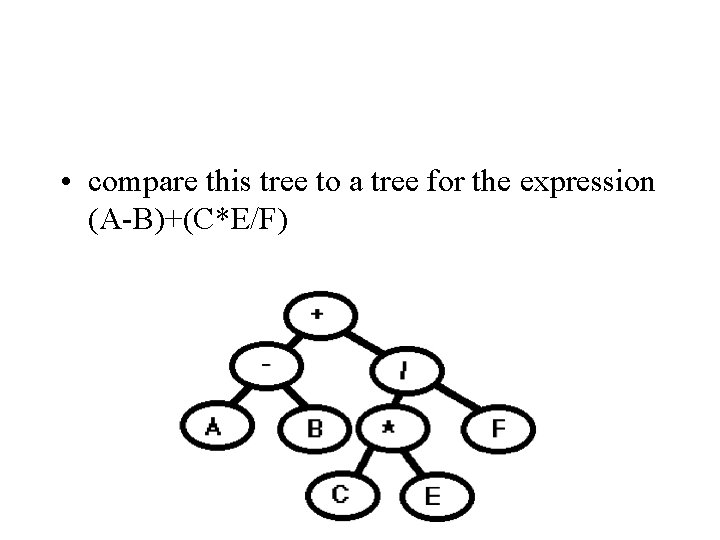
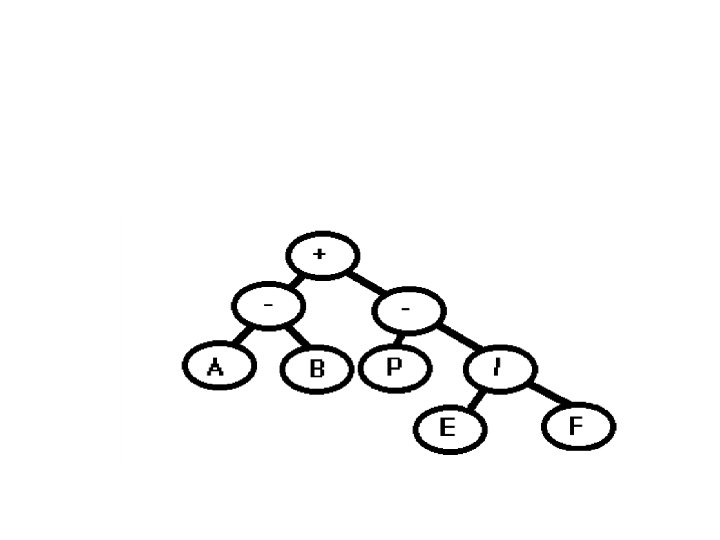
Trees representing arithmetic expressions. • For example: (A-B)+(C*(E/F))

Example

• compare this tree to a tree for the expression (A-B)+(C*E/F)

• Notice how small changes in the order of operations (like removing a set of parentheses) make major changes in the structure of the tree.

Reverse Polish Again!? ! • Recall that expressions are easily evaluated using a stack if they are available in postfix form: AB-CEF/*+ • Trees can be traversed in such a way as to produce the postfix form. eg. a postorder traversal yields the postfix form of the expression. • More on this later.

Implementing Binary Trees • Two methods: • 1. Linear representation - array • 2. Linked representation - pointers

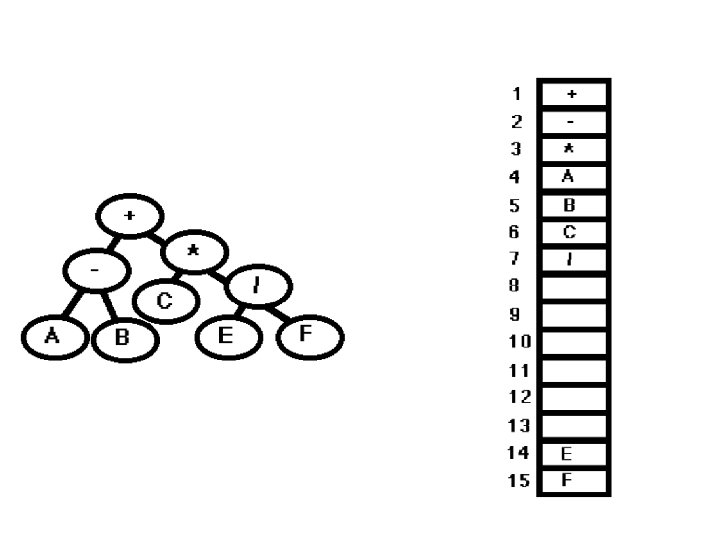
Linear representation (Depth=3) • 1. Allocate an array of size 2^(d+1)-1 • 2. Store root in location 1 • 3. For node in location n, store left child in location 2 n, right child in location 2 n+1

Tradeoffs • 1. Fast access (given a node, its children and parent can be found very quickly) • 2. Slow updates (inserts and deletions require physical reordering) • 3. Wasted space (partially filled trees)

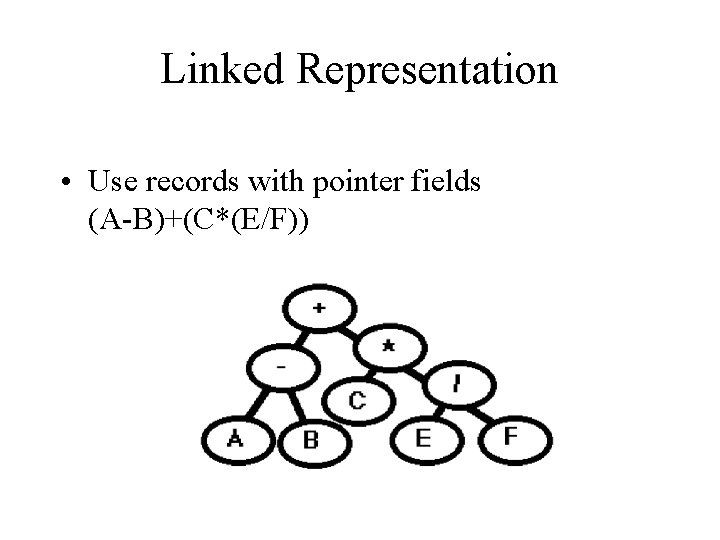
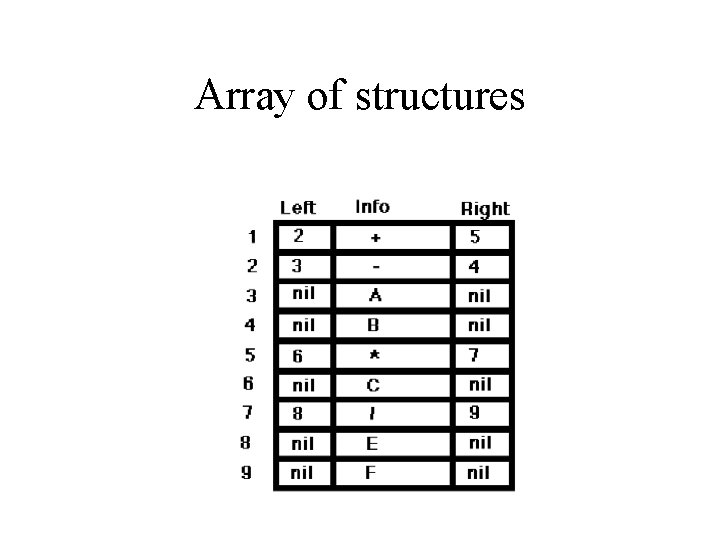
Linked Representation • Use records with pointer fields (A-B)+(C*(E/F))

Using an array of records • The array implementation of this ADT looks like this (next slide) • Insertions and deletions involve only manipulation of pointers

Array of structures

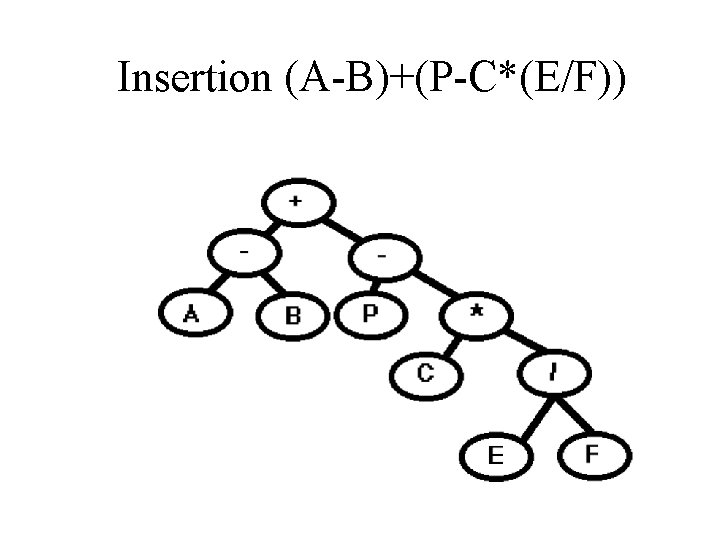
Insertion (A-B)+(P-C*(E/F))

Deletion (A-B)+(P-E/F) • The changes to the array of records look like this after both of the operations (insertion of -P and deletion of *C) have been performed.

Tradeoffs • 1. Faster updates • 2. Extra memory for pointers • 3. Wasted space for nil pointers (can be corrected by threading) • 4. Difficult to determine a node's parent (corrected by adding a parent pointer)

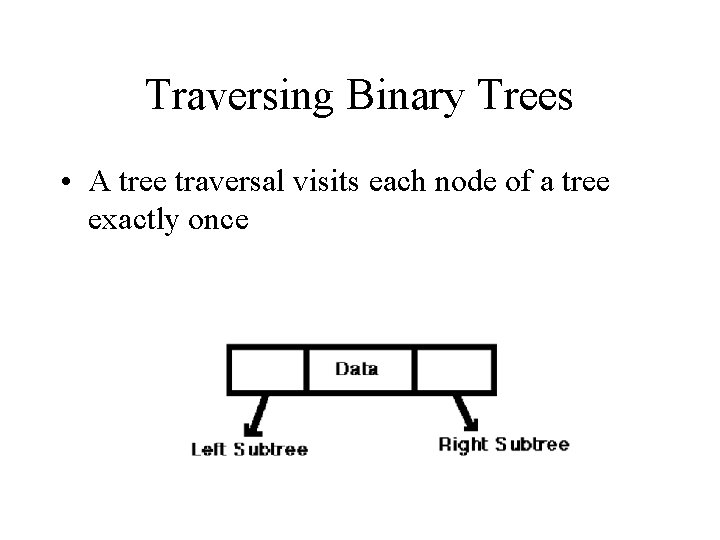
Traversing Binary Trees • A tree traversal visits each node of a tree exactly once

Modes of traversal • When visiting a node we have three choices • 1. Process the data • 2. Remember location of the current node and process nodes in the left subtree • 3. Remember location of the current node and process nodes in the right subtree The choice made dictates the order of node processing for the entire tree

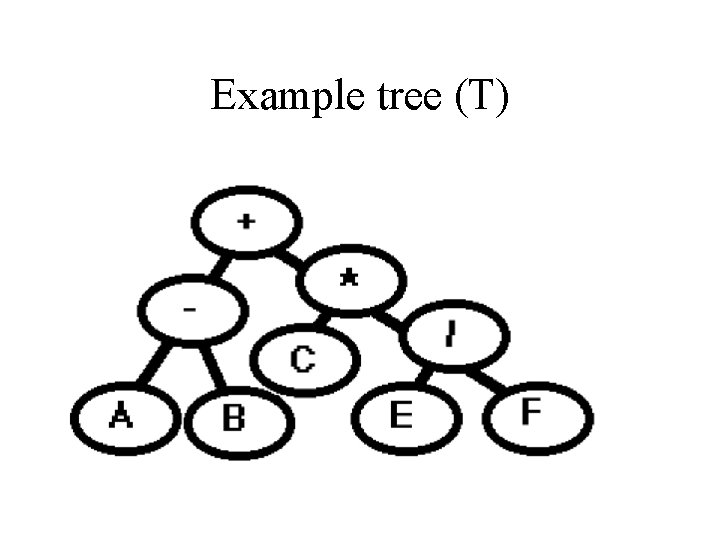
Example tree (T)

Steps for a Preorder traversal of a binary tree • 1. Process root • 2. Do a preorder traversal of the nodes subtree(recursively) in the root's left • 3. Do a preorder traversal of the nodes subtree (recursively) in the root's right

• Assume the we have a procedure called Process that simply writes out the data contained in any given node. • Then, using process, a preorder traversal of tree T produces +=AB*C/EF (the prefix form of (A-B)+C*(E/F))

Steps for an Inorder traversal of a binary tree • 1. Recursively visit left subtree • 2. Process root • 3. Recursively visit right sub-tree

Steps for a Postorder traversal of a binary tree • 1. Recursively visit left subtree • 2. Recursively visit right subtree • 3. Process Root

• A postorder traversal of T produces AB- CEF/*+ (the postfix form) • These traversals can be done on any binary tree, not just expression trees.

Implementing lists using binary trees

Implementing the List ADT • Vehicle • Array • Linked • Binary Tree Advantage Disadvantage Fast search O(log 2 N) O(N) Fast inserts and deletions O(1) Fast inserts and deletions O(log 2 N) Slow inserts and deletions Slow search List O(N) Tree must be balanced The hierarchical relationship we employed is the ordering property.

Example tree: T 1

• Inorder traversal of this tree gives ADEFGHKMNPSTUVZ So: An inorder traversal of a binary tree with the ordering property visits the nodes in ascending order.

• Adding a node to a binary tree with the ordering property • Follow the insertion rule: "If less than, go left, otherwise go right. "

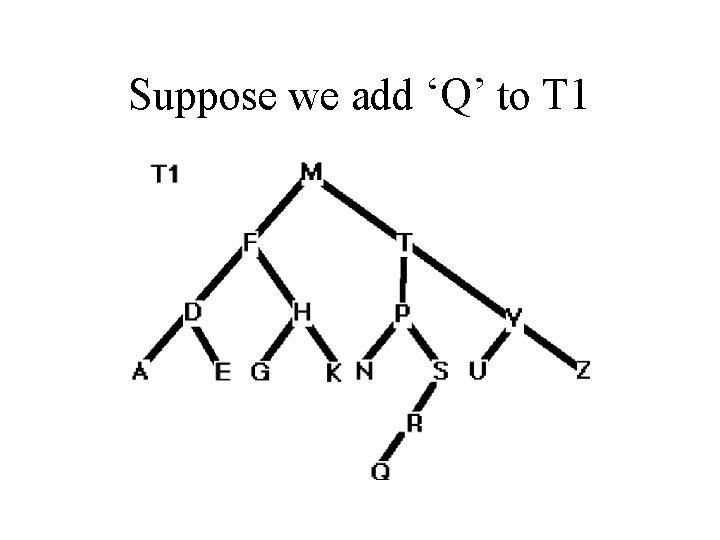
Example: Add the letter R to the previous tree. • 1. Compare R to M (the root). Since R > M, add R to the right subtree • 2. Compare R to T (the root of the subtree). Since R < T go left • 3. Compare R to P. Since R > P go right • 4. Compare R to S. Since R < S go left • 5. Since the left subtree is NULL add R at this point Clearly, the procedure is recursive.

Adding ‘R’ to the tree

Efficiency of adding to a binary tree • Question: How many comparisons did we have to make? Answer: 4 (ie. depth + 1)

Differing tree configurations • Consider another tree: T 2 representing the same list:

Question • How many comparisons do we have to make to add the letter R? Answer: 9 (ie. depth + 1)

Question: • How do you minimize the depth of a binary tree? Answer: Make sure it is full, or balanced.

Definition: • A balanced binary tree is one in which every node above level depth-1 has exactly two children.

Depth to size comparisons • When a binary tree of N nodes is balanced, no branch will be longer than log(base 2)N+1. Thus, the efficiency of the adding algorithm is O(log(base 2)N) • Depth • 0 1 2 3. . . 9 10 Max. N 1 3 7 15 1023 1 million

Suppose we add ‘Q’ to T 1

Suppose we add Q to T 1: • Now T 1 is not balanced. • There are methods for balancing trees.

Recall the binary search of an array

Binary similarities • Each probe into the array is analogous to a recursive descent in the search of a binary tree. (both are O(log 2 N))

Deleting from a tree

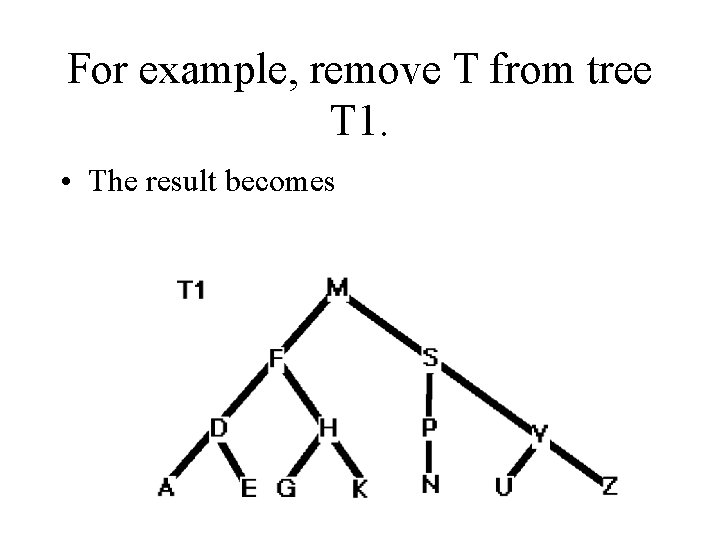
For example, remove T from tree T 1. • The result becomes

Deletion strategies • Requirement: The resulting tree must have the ordering property. • One method is to find the largest item in T 1's left sub-tree and replace T with it.

Three special cases which might occur: • 1. Node to be deleted has a left child • 2. Node to be deleted has a right child but no left child • 3. Node to be deleted has no children

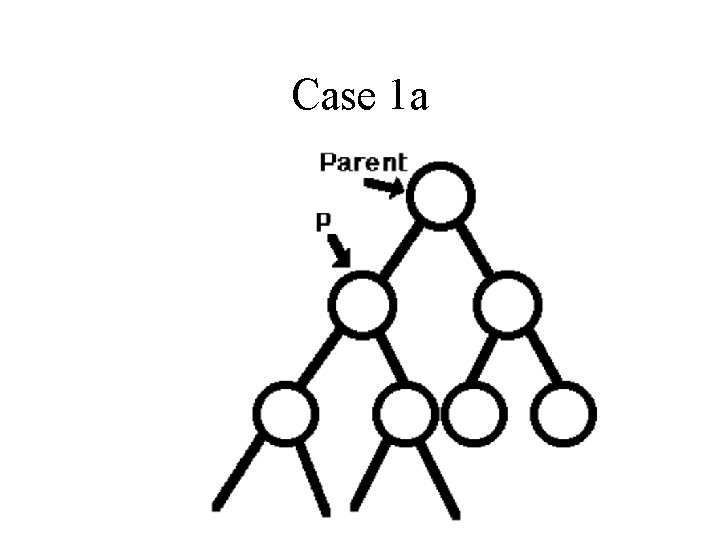
Case 1: • Suppose P points to the node to be deleted. There are two important subcases • 1. a P->Left has no right child • 1. b P->Left has a right child

Case 1 a

Case 1 b

Case 2

Case 3

List comparison • Tradeoffs • adding searching Linked List O(1) O(N) • user 1 ptr/node memory • system stack minimal Binary Tree O(1) & deleting O(log 2 N) balanced O(N) worst case 2 ptrs/node (many NULL) recursion (remedy - threading)

General Trees

General Trees • So far we have been studying binary trees, general trees however can have more than two children for each node. Question: Does the former restriction to binary trees mean that we cannot apply what we have learned to general trees? Answer: No! As long as we are willing to convert general trees to binary ones.

Binary version of general tree

Preorder Traversal • (Root, Left, Right) • JBDNEPQKLMCXRT

Processing order • 1. Process root 2. Recursively traverse the left-most subtree 3. Recursively traverse the next subtree to the right 4. Repeat step 3 until there are no more subtrees

Postorder Traversal • (Left, Right, Root) • QPENDLXRCTMKBJ

• Note that this order on the general tree can be described by: 1. Start at the leaves and work up 2. Process a node after all nodes below it have been processed