Introduction to thermodynamics 1 Basics of chemical thermodynamics

Introduction to thermodynamics 1. Basics of chemical thermodynamics 2. Methods of thermodynamic value measurements

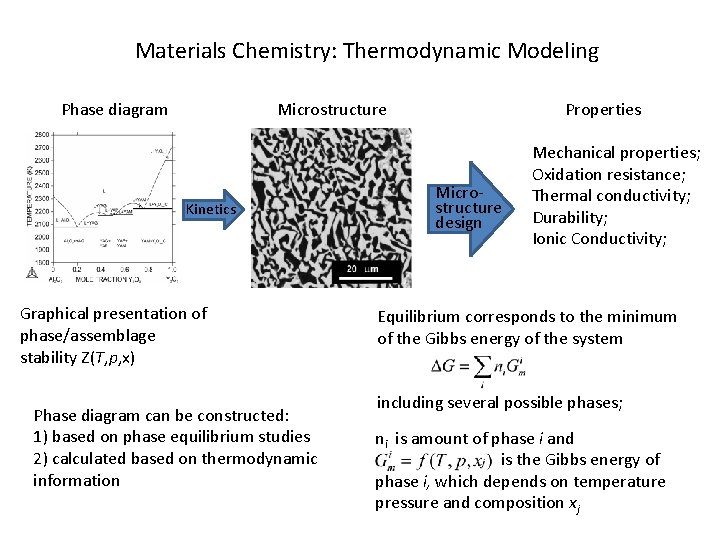
Materials Chemistry: Thermodynamic Modeling Phase diagram Microstructure Kinetics Graphical presentation of phase/assemblage stability Z(T, p, x) Phase diagram can be constructed: 1) based on phase equilibrium studies 2) calculated based on thermodynamic information Properties Microstructure design Mechanical properties; Oxidation resistance; Thermal conductivity; Durability; Ionic Conductivity; Equilibrium corresponds to the minimum of the Gibbs energy of the system including several possible phases; ni is amount of phase i and is the Gibbs energy of phase i, which depends on temperature pressure and composition xj

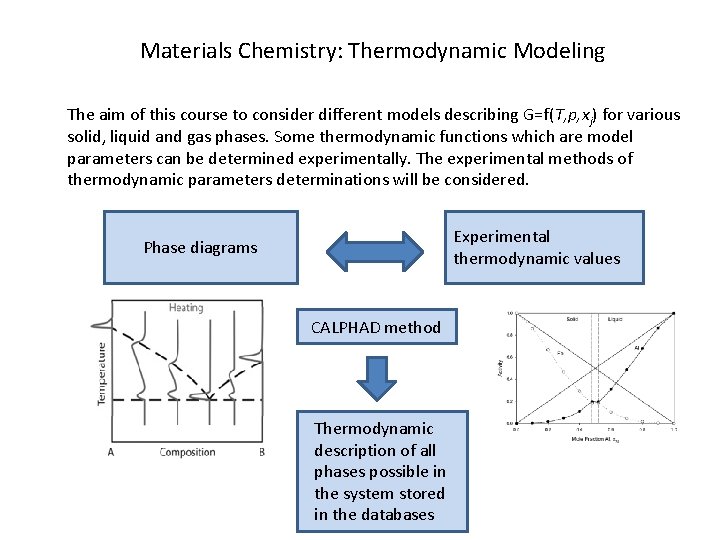
Materials Chemistry: Thermodynamic Modeling The aim of this course to consider different models describing G=f(T, p, xj) for various solid, liquid and gas phases. Some thermodynamic functions which are model parameters can be determined experimentally. The experimental methods of thermodynamic parameters determinations will be considered. Experimental thermodynamic values Phase diagrams CALPHAD method Thermodynamic description of all phases possible in the system stored in the databases

Basic definitions System is a part of Universe chosen for investigation. Properties are defined and measurable features of a system. Intensive variables are independent on amount of materials present. They are not additive. Extensive variables are proportional to the amount of materials. They are additive. System boundaries: System is separated from surroundings by boundaries. Isolated systems no exchange of energy or matter with the surroundings. Closed systems can exchange energy with surrounding, but transfer of matter is prohibited. Open system can exchange both energy and matter with the surroundings. Phase is homogeneous part of the system having the same properties and composition and separated by interface from other part of the system. Constituent (Species) are particles which can exist in the system. They can be elements, molecules or ions. Components are minimal numbers of constituents, which can describe composition of any phase of the system and can be separated from the system and exist independently. Elements or compounds can be selected as components.

First law of thermodynamics A phase possesses internal energy due to kinetic and potential energy of it molecules or atoms. Changes in internal energy is manifested as change of temperature. The first law is the principle of conservation of energy. In the closed system the heat transferred to a system is spent to change of internal energy and work done by the system: Q=DU+A, where Q is heat transferred to the system, DU is the change of internal energy and A is the work done by the system Work A is positive when the work is done by the system and negative when work is done on the system (convention), but it can be accepted vise versa. Internal energy U is function of state of the system, since it does not depends on the way passed by the system. Work and heat are not functions of state, since they depend on the way passed by the system. d. Q=d. U+d. A Law of Hess: Heat effect of the reaction does not depend on intermediate stages and it is determined by nature and state of initial substances and final products. Reactions can be exothermic (releasing heat ) and endothermic (consuming heat). Law of Joule: When gas expands without doing work into a chamber that has been evacuated and without taking in or giving out heat, the temperature of gas does not change. Therefore internal energy is not changing though the volume of gas changes. The law is valid for ideal gas.

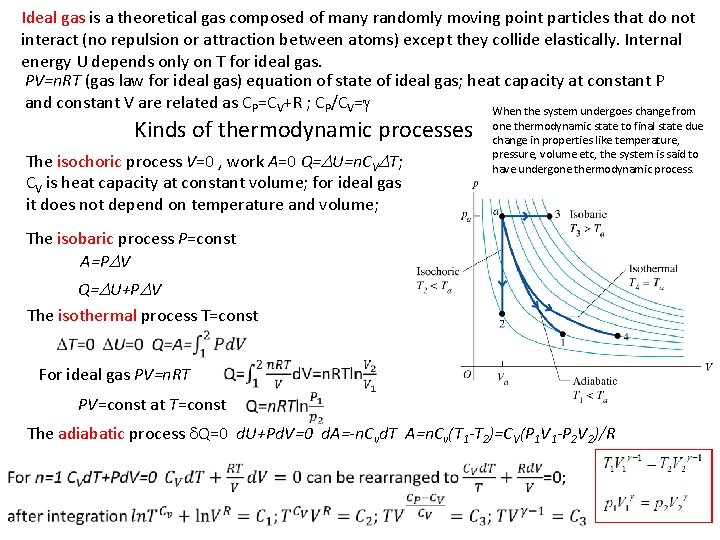
Ideal gas is a theoretical gas composed of many randomly moving point particles that do not interact (no repulsion or attraction between atoms) except they collide elastically. Internal energy U depends only on T for ideal gas. PV=n. RT (gas law for ideal gas) equation of state of ideal gas; heat capacity at constant P and constant V are related as CP=CV+R ; CP/CV=g When the system undergoes change from Kinds of thermodynamic processes The isochoric process V=0 , work A=0 Q=DU=n. CVDT; CV is heat capacity at constant volume; for ideal gas it does not depend on temperature and volume; one thermodynamic state to final state due change in properties like temperature, pressure, volume etc, the system is said to have undergone thermodynamic process. The isobaric process P=const A=PDV Q=DU+PDV The isothermal process T=const For ideal gas PV=n. RT PV=const at T=const The adiabatic process d. Q=0 d. U+Pd. V=0 d. A=-n. Cvd. T A=n. Cv(T 1 -T 2)=CV(P 1 V 1 -P 2 V 2)/R

Second law of thermodynamics introduces entropy S as function of state d. Q/T=d. S The heat can not spontaneously transfer from cold to the hot body. It is not possible to reach temperature of 0 K. Classical thermodynamics approach: Carnot cycle: considering reversible processes consisting from two isothermal processes at T 1 and T 2 (T 1>T 2) and two adiabatic processes (in isolated systems). Carnot cycle on P-V diagram At the first and second stages work is done by the system and at the third and fourth stages work is done on the system to return it in initial state. Efficiency of Carnot cycle is equal to: Carnot cycle can be reversed , in which it operates as refrigerator.

Second law of thermodynamics The entropy is a measure of the amount of energy which is unavailable to do work. It is impossible to construct a heat engine that operating in the cycle produce no effect other than adsorption of energy from one reservoir and performance of an equal amount of work. Statistical thermodynamics approach Physical meaning : S=k. B ln. W k. B – Boltzmann constant equal to R/NA, where NA is Avogadro number, W – number of different microscopic states available in the system. Entropy is a measure of disorder and a measure of multiplicity of the system.

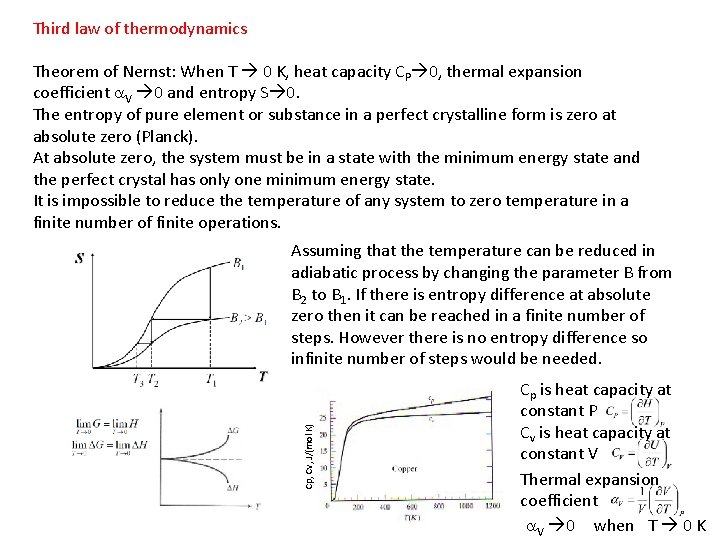
Third law of thermodynamics Theorem of Nernst: When T 0 K, heat capacity CP 0, thermal expansion coefficient a. V 0 and entropy S 0. The entropy of pure element or substance in a perfect crystalline form is zero at absolute zero (Planck). At absolute zero, the system must be in a state with the minimum energy state and the perfect crystal has only one minimum energy state. It is impossible to reduce the temperature of any system to zero temperature in a finite number of finite operations. Cp, Cv, J/(mol K) Assuming that the temperature can be reduced in adiabatic process by changing the parameter B from B 2 to B 1. If there is entropy difference at absolute zero then it can be reached in a finite number of steps. However there is no entropy difference so infinite number of steps would be needed. Cp is heat capacity at constant P Cv is heat capacity at constant V Thermal expansion coefficient a. V 0 when T 0 K

Functions of state and interrelations between them Internal energy U=TS-PV d. U=Td. S-Pd. V Enthalpy H=U+PV d. H=Td. S+Vd. P Helmholtz energy F=U-TS d. F=-Sd. T-Pd. V Gibbs energy G=U-TS+PV=H-TS d. G=-Sd. T+Vd. P Maxwell equations (second derivative):

Thermodynamic equilibrium and reversible processes Thermodynamic equilibrium is internal state of single thermodynamic system, or relation between several systems connected by permeable or impermeable walls. In thermodynamic equilibrium there is no net macroscopic flows of matter or of energy, either within a system or between systems. In a system in the state of internal thermodynamic equilibrium, no macroscopic change occurs. A reversible process is a process whose direction can be "reversed" by inducing infinitesimal changes to some property of the system via its surroundings, while not increasing entropy. Throughout the entire reversible process, the system is in thermodynamic equilibrium with its surroundings. Since it would take an infinite amount of time for the reversible process to finish, perfectly reversible processes are impossible. However, if the system undergoing the changes responds much faster than the applied change, the deviation from reversibility may be negligible. A quasi-static process is a thermodynamic process that happens slowly enough for the system to remain in internal equilibrium. Any reversible process is necessarily a quasi-static one. However, some quasi-static processes are irreversible, if there is heat flowing (in to or out of the system) or if entropy is being created in some way. In a reversible cycle, the system and its surroundings will be returned to their original states. Thermodynamic processes can be carried out in one of two ways: reversibly or irreversibly. Reversibility refers to performing a reaction continuously at equilibrium. In an ideal thermodynamically reversible process, the energy from work performed by or on the system would be maximized, and that from heat would be minimized.

Conditions for equilibrium and spontaneous change d. G=0 (minimum G) Equilibrium at constant T and P (T and P are characteristic state variable) d. G<0 Spontaneous change at constant T and P d. F=0 (minimum F) Equilibrium at constant T and V (T and V are characteristic state variables) d. F<0 Spontaneous change at constant T and V d. S=0 (maximum S) Equilibrium at constant U and V – isolated system (U and V are characteristic state variables) d. S>0 Spontaneous change at constant U and V Functions of state have an extremum at equilibrium if the characteristic state variables are kept constant

Heat capacity is amount of heat need to transfer to a body to raise its the temperature by 1 K Standard entropy at 298 K Kirchhoff‘s law b is compressibility, a is thermal expansion Compressibility and expansion

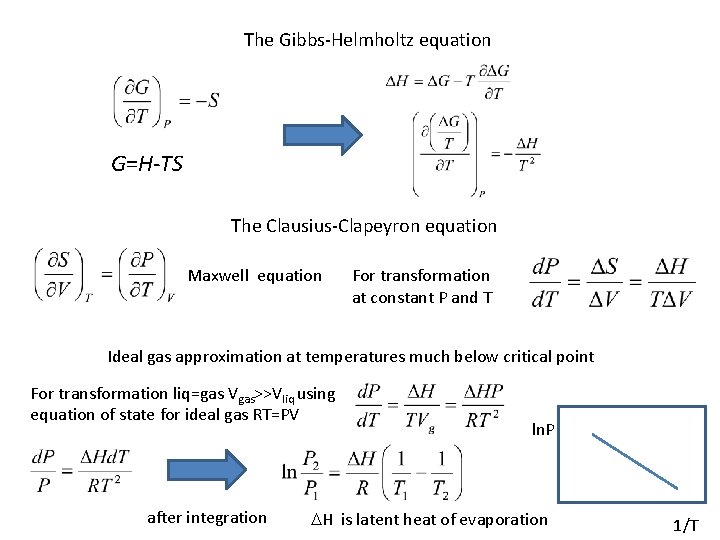
The Gibbs-Helmholtz equation G=H-TS The Clausius-Clapeyron equation Maxwell equation For transformation at constant P and T Ideal gas approximation at temperatures much below critical point For transformation liq=gas Vgas>>Vliq using equation of state for ideal gas RT=PV after integration ln. P DH is latent heat of evaporation 1/T

Composition as a variable Partial molar properties and chemical potentials Thermodynamic functions can depend on composition e. g. G(P, T, n 1, n 2, … nk) mi – chemical potential ni – number of moles of component or species - partial molar volume Partial molar properties are intensive parameters Fundamental equations for open systems d. U=Td. S-Pd. V+Smidni d. H=Td. S+Vd. P+Smidni d. F=-Sd. T-Pd. V+Smidni d. G=-Sd. T+Vd. P+Smidni These equations are valid for open or close systems where composition changes due to mass transfer or reaction between species

Gibbs- Duhem equation d. G=Smidni+Snidmi The Gibbs energy change due to adding or removing material at constant P and T -Sd. T+Vd. P=Snidmi in equilibrium at constant T and P other forms of the Gibbs-Duhem equation

Raoult‘s law, ideal solutions Partial pressure of solvent (component 1) is proportional to its mole fraction in the solution. The law is valid for dilute solution of not volatile component in volatile solvent. P 1 is pressure of solvent over solution, x 1 – mole fraction of solvent, P 01 is pressure of saturated vapour of solvent over pure solvent Ideal solution is a solution for which each component i obeys Raoult‘s law and chemical potential for each component i is expressed: In real solutions ai=gixi ai is activity, gi is coefficient of activity

Activity, coefficient of activity, standard state Definition of activity of component i is equal: mi – chemical potential - chemical potential in standard state Activity is “effective” concentration at which phase would behave as ideal Standard state can be selected as pure component at given P and T or as state of infinite dilute solution Coefficient of activity gi relates activity to measured concentration ai=gixi Substituting mi in equation of Gibbs-Duhem by different form of Gibbs-Duhem equation can be derived

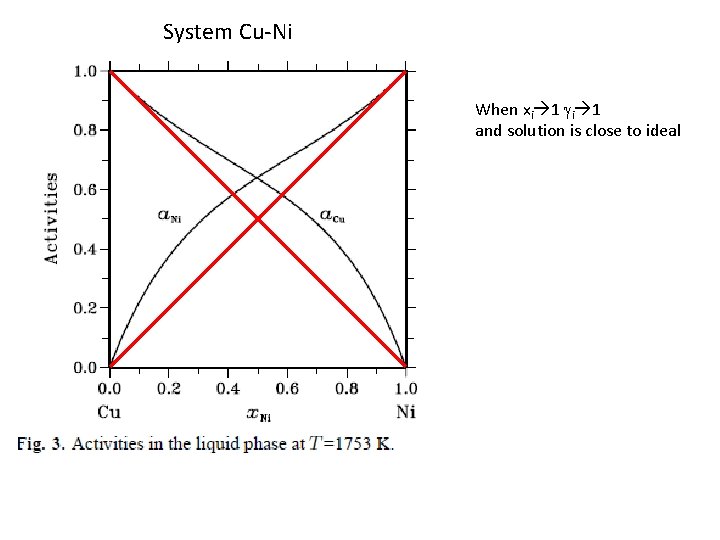
System Cu-Ni When xi 1 gi 1 and solution is close to ideal

Ideal solutions and real solutions: positive and negative deviation from ideal behaviour Ideal solution G G=xi. G 0 i+xj. G 0 j+RT(xilnxi+xjlnxj) Model of regular solution G G 0 L>0 x 1 x 2 x a Gm=xi. G 0 i+xj. G 0 j+RT(xilnxi+xjlnxj)+0 Lijxixj 0 L<0 x 1 a Real solutions x x

Henry‘s law for diluted solutions Solubility of gas in liquid is proportional to pressure of this gas over liquid C=K∙P, where C is concentration of component in liquid (mol/l), K – temperature dependent parameter and P is pressure Concentration C=ngas/Vliq; For ideal gas n. RT=PVgas and law of Henry for ideal gas is expressed as PVgas/(RTVliq)=KP and Vgas/Vliq=KRT Coefficient of solubility Vgas/Vliq of ideal gas does not depend on gas pressure. activity Roult‘s law xi 1 and solutions are ideal; Henry‘s law xi 0 and solutions are not ideal, but activity linearly depends on concentration ai=g 0 ixi , where g 0 i is Henrian parameter or activity coefficient in infinite dilute solution concentration

Models for very dilute solutions ai=g 0 ixi , where g 0 i is Henrian parameter or activity coefficient in infinite dilute solution Wagner‘s formalism (i 2) g 0 i is activity coefficient at infinite dilution x 1 1, eij are first-order interaction parameters Comparison with regular solution model: Wagner‘s dilute solution model Regular solution model For very dilute solutions Darken‘s quadratic formalism 1 is solvent, a 12 and C 2 are constants If C 2 =0 the Darken‘s model is equivalent to regular solution model

Chemical equilibrium, constant of reaction Reaction can occur in multicomponent homogeneous system at constant P and T Smidni=0 mi=m 0 i+RTlnai a. A + b. B = c. C + d. D Dr. G 0+RTln. Ka=0 for gas phase for condensed phase i- reactant, j- products, n-stoichiometric coefficients

Examples: heterogeneous and homogeneous reactions Fe + CO 2 = Fe. O + CO 3 phases participate in the reaction Fe, Fe. O and gas (CO, CO 2) 2 CO + O 2 = 2 CO 2 Reaction occurs in single phase gas

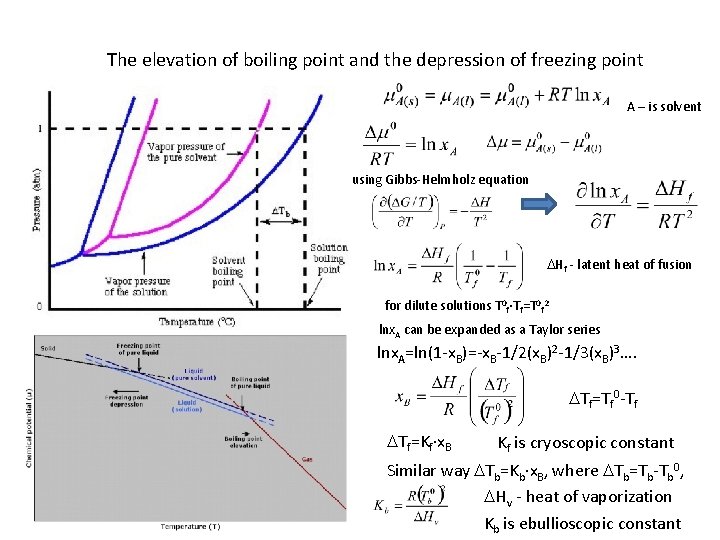
The elevation of boiling point and the depression of freezing point A – is solvent using Gibbs-Helmholz equation DHf - latent heat of fusion for dilute solutions T 0 f∙Tf=T 0 f 2 lnx. A can be expanded as a Taylor series lnx. A=ln(1 -x. B)=-x. B-1/2(x. B)2 -1/3(x. B)3…. DTf=Tf 0 -Tf DTf=Kf∙x. B Kf is cryoscopic constant Similar way DTb=Kb∙x. B, where DTb=Tb-Tb 0, DHv - heat of vaporization Kb is ebullioscopic constant

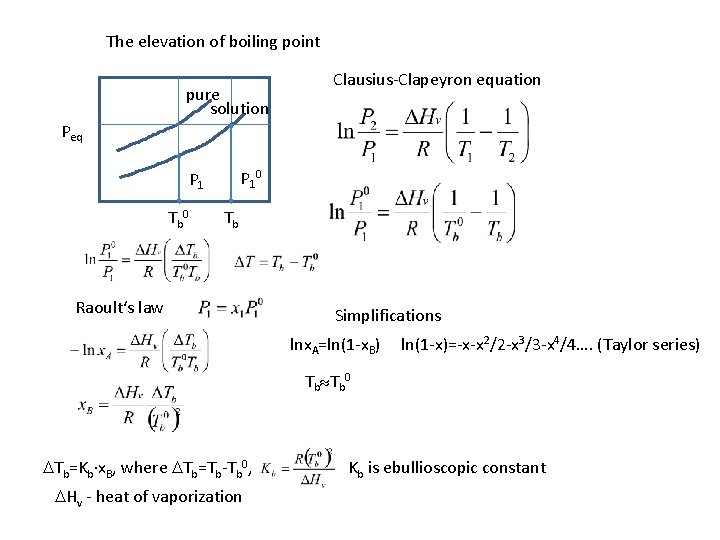
The elevation of boiling point pure solution Peq Clausius-Clapeyron equation pure P 10 P 1 Tb 0 Tb Raoult‘s law Simplifications lnx. A=ln(1 -x. B) ln(1 -x)=-x-x 2/2 -x 3/3 -x 4/4…. (Taylor series) Tb Tb 0 DTb=Kb∙x. B, where DTb=Tb-Tb 0, DHv - heat of vaporization Kb is ebullioscopic constant

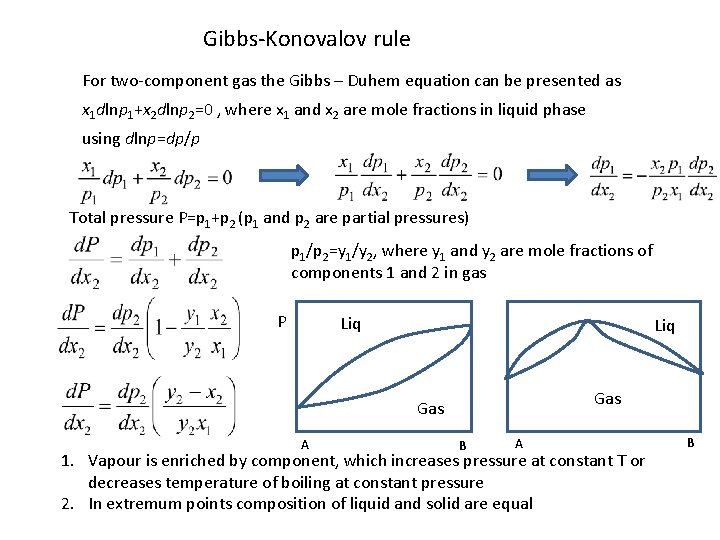
Gibbs-Konovalov rule For two-component gas the Gibbs – Duhem equation can be presented as x 1 dlnp 1+x 2 dlnp 2=0 , where x 1 and x 2 are mole fractions in liquid phase using dlnp=dp/p Total pressure P=p 1+p 2 (p 1 and p 2 are partial pressures) p 1/p 2=y 1/y 2, where y 1 and y 2 are mole fractions of components 1 and 2 in gas P Liq Gas A B A 1. Vapour is enriched by component, which increases pressure at constant T or decreases temperature of boiling at constant pressure 2. In extremum points composition of liquid and solid are equal B

Gibbs-Konovalov rule for ternary system B xs TB>TA>TC B s s xs xl l xl A C TA<T 1<TB B l C A TC<T 2<TA A and C decrease T, B increases T s should be enriched by B, l should be enriched by A and C C decrease T, B and A increases T s should be enriched by B and A, l should be enriched by C s xs xl A T 3=TA A has little influence to T, C decrease T, B increase T, tie lines are parallel to side B-C or slightly deviate l C

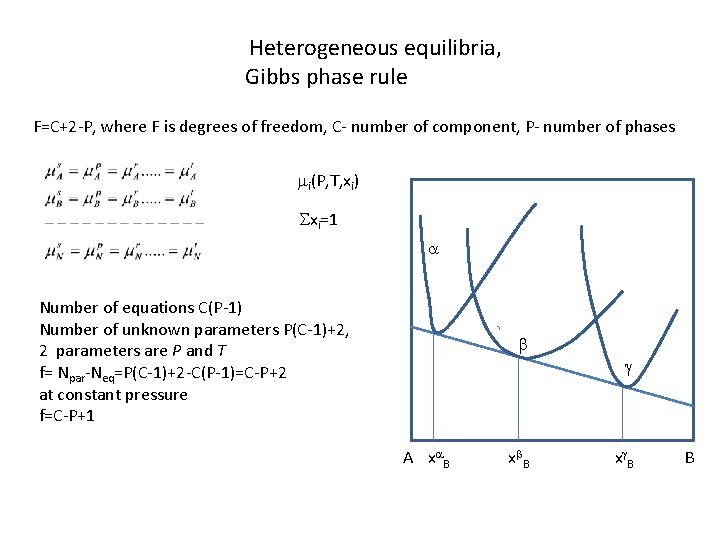
Heterogeneous equilibria, Gibbs phase rule F=C+2 -P, where F is degrees of freedom, C- number of component, P- number of phases mi(P, T, xi) Sxi=1 a Number of equations C(P-1) Number of unknown parameters P(C-1)+2, 2 parameters are P and T f= Npar-Neq=P(C-1)+2 -C(P-1)=C-P+2 at constant pressure f=C-P+1 b g A xa B xb. B xg. B B

Methods of measurements of thermodynamic quantities Low temperature heat capacity measurements and entropy determination Adiabatic calorimetry CP from very low temperatures to temperatures around 400 K Q is heat measured in calorimeter with sample of mass m Q 0 is heat in empty crucible, DT is increase in temperature Standard entropy can be calculated by CP/T integration at T< 20 K CP=a. T 3

Solution calorimetry: measure enthalpy of solution (in HF, HF-HCl, 2 Pb. O∙B 2 O 3, 3 Na 2 O ∙ 4 Mo. O 3, (Na 0, 48, Li 0, 52)BO 2 Enthalpy of formation of La. YO 3 by drop-solution calorimetry N Reaction Dr. H (k. J) (1) La 2 O 3(s, 298. 15 K)→La 2 O 3(s, 973 K) 83. 83 [31] (2) La 2 O 3(s, 973 K)→dilute solution in 2 Pb. O. B 2 O 3 (973 K) -126. 0± 4. 4 [29] (3) Y 2 O 3(s, 298. 15 K)→Y 2 O 3(s, 973 K) 81. 94 [31] (4) Y 2 O 3(s, 973 K)→ dilute solution in 2 Pb. O. B 2 O 3 (973 K) -61. 7± 1. 1 [30] (5) La. YO 3(s, 298. 15 K)→ dilute solution in 2 Pb. O. B 2 O 3 (973 K) 39. 9± 2. 4 * (6) 0. 5 La 2 O 3(s, 298. 15 K)+0. 5 Y 2 O 3(s, 298. 15 K) = La. YO 3(s, 298. 15 K) Dr(6)H = 0. 5 Dr(1)H + 0. 5 Dr(2)H + 0. 5 Dr(3)H + 0. 5 Dr(4)H - Dr(5)H -50. 87± 4. 0 Direct reaction calorimetry: measure heat of reaction initiated in closed insulated container x. A+y. B Ax. By Reagents A and B mixed in ratio x/y in crucible are dropped into calorimeter at Tc If reaction is complete, the total amount of heat is measured: Q 1=DH(C, Tc-Tr)+DH(A, Tc-Tr)+DH(B, Tc-Tr)+Df. H(Ax. By, Tc) The second drop already reacted sample Q 2=DH(C, Tc-Tr)+DH(Ax. By, Tc-Tr) Q 1 -Q 2=Df. H(Ax. By) at 298 K

Combustion bomb calorimetry: measure of combustion reaction at constant volume x. M+y/2 O 2=Mx. Oy DUcomb=CVDT, CV is heat capacity of calorimeter and content DHcomb=DUcomb+DPV DHcomb=DUcomb+RTcomb. Dngas Calibration using substance with known DHcomb (benzoic acid) Partial enthalpy measurements: Small amounts of metal i are dropped into calorimeter containing melted element j, Fi –area under measured temperature-time curve DH 298 T 0 is enthalpy of heating from 298 to T 0 (T 0 is initial temperature of calorimeter at x=0, W – thermal equivalent of calorimeter, DT(x)=T(x)-T 0, DHTr, i – enthalpy of fusion if T<Tfus, i, CP, i – heat capacity

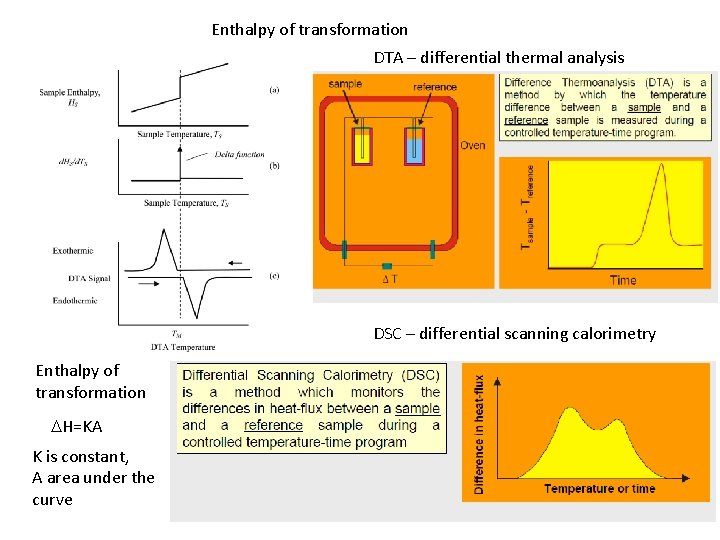
Enthalpy of transformation DTA – differential thermal analysis DSC – differential scanning calorimetry Enthalpy of transformation DH=KA K is constant, A area under the curve

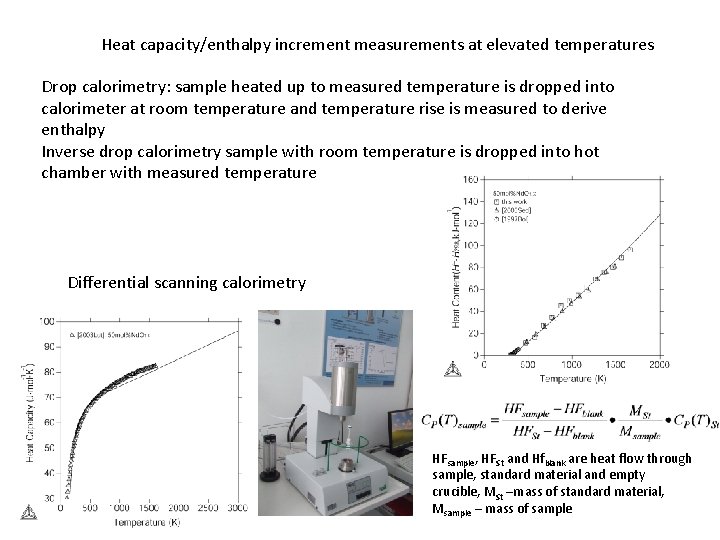
Heat capacity/enthalpy increment measurements at elevated temperatures Drop calorimetry: sample heated up to measured temperature is dropped into calorimeter at room temperature and temperature rise is measured to derive enthalpy Inverse drop calorimetry sample with room temperature is dropped into hot chamber with measured temperature Differential scanning calorimetry HFsample, HFSt and Hfblank are heat flow through sample, standard material and empty crucible, MSt –mass of standard material, Msample – mass of sample

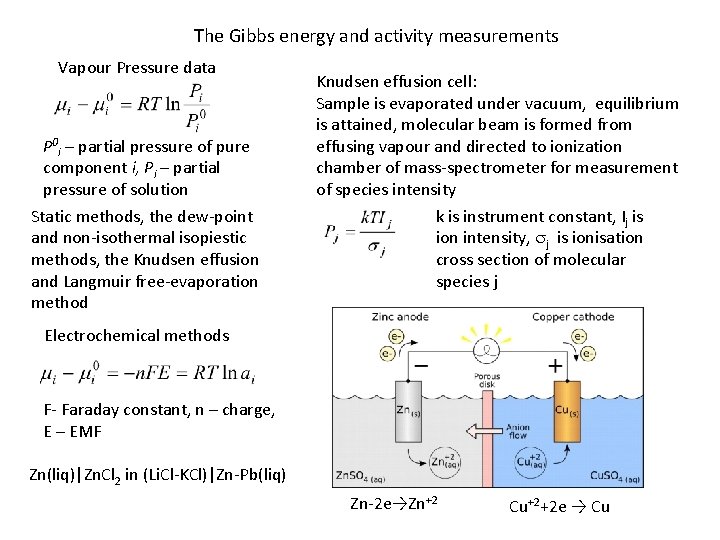
The Gibbs energy and activity measurements Vapour Pressure data P 0 i – partial pressure of pure component i, Pi – partial pressure of solution Static methods, the dew-point and non-isothermal isopiestic methods, the Knudsen effusion and Langmuir free-evaporation method Knudsen effusion cell: Sample is evaporated under vacuum, equilibrium is attained, molecular beam is formed from effusing vapour and directed to ionization chamber of mass-spectrometer for measurement of species intensity k is instrument constant, Ij is ion intensity, sj is ionisation cross section of molecular species j Electrochemical methods F- Faraday constant, n – charge, E – EMF Zn(liq)|Zn. Cl 2 in (Li. Cl-KCl)|Zn-Pb(liq) Zn-2 e→Zn+2 Cu+2+2 e → Cu