Introduction to the Simplex Method to solve Linear

Introduction to the Simplex Method to solve Linear Programs Eric Feron Spring 2001 16. 410: Eric Feron / MIT, Spring 2001

Algorithms • The simplex algorithm: before all, an algorithm • The way an algorithm works: –Initialization step –Iteration step –Optimality test (stopping rule) No? Yes? –Exit 16. 410: Eric Feron / MIT, Spring 2001

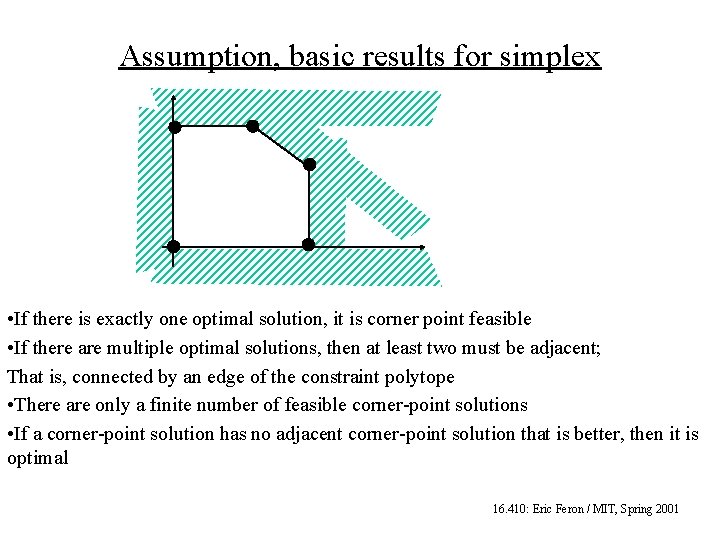
Assumption, basic results for simplex • If there is exactly one optimal solution, it is corner point feasible • If there are multiple optimal solutions, then at least two must be adjacent; That is, connected by an edge of the constraint polytope • There are only a finite number of feasible corner-point solutions • If a corner-point solution has no adjacent corner-point solution that is better, then it is optimal 16. 410: Eric Feron / MIT, Spring 2001

Essence of the simplex method • Step 1: Start at a corner-point feasible solution (Initialization) • Step 2: Move to a better adjacent feasible solution • Step 3: Optimality test. The corner-point solution is optimal when no better adjacent corner-point solution can be found. • A really simple algorithm, if we have good book keeping procedures. 16. 410: Eric Feron / MIT, Spring 2001

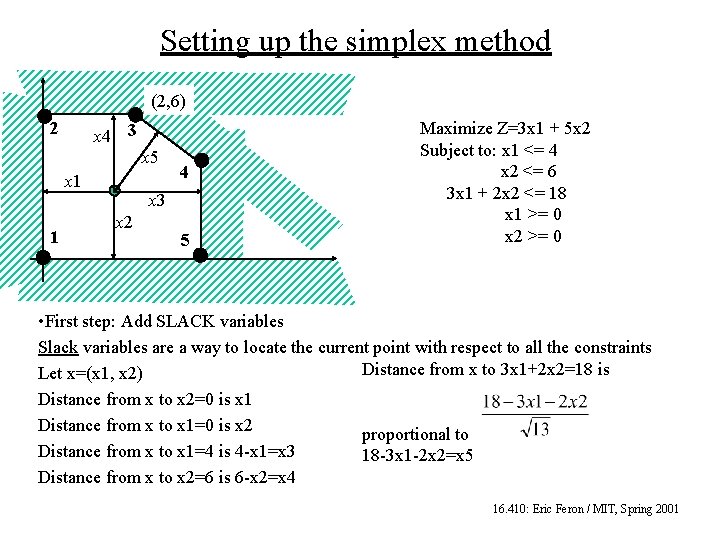
Setting up the simplex method (2, 6) 2 x 4 3 x 5 x 1 1 4 x 3 x 2 5 Maximize Z=3 x 1 + 5 x 2 Subject to: x 1 <= 4 x 2 <= 6 3 x 1 + 2 x 2 <= 18 x 1 >= 0 x 2 >= 0 • First step: Add SLACK variables Slack variables are a way to locate the current point with respect to all the constraints Distance from x to 3 x 1+2 x 2=18 is Let x=(x 1, x 2) Distance from x to x 2=0 is x 1 Distance from x to x 1=0 is x 2 proportional to Distance from x to x 1=4 is 4 -x 1=x 3 18 -3 x 1 -2 x 2=x 5 Distance from x to x 2=6 is 6 -x 2=x 4 16. 410: Eric Feron / MIT, Spring 2001

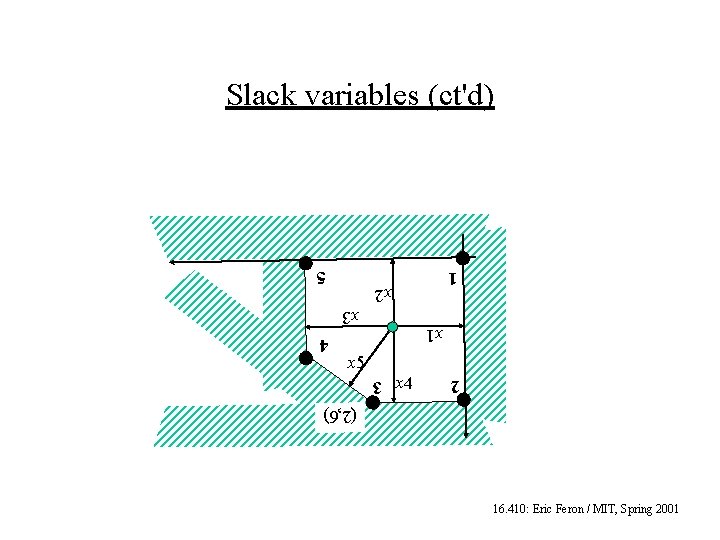
Salck variables (ct'd) • So we can characterize the position of any point x in the decision space by its distance to all the constraints x 1, x 2, x 3, x 4, and x 5 • That's a new, generalized coordinate system (obviously highly redundant) • Any corner point is the intersection of two constraints: For example the origin 1 is the intersection of x 1>= 0 and x 2>=0 • In general, corner points are defined by two of the generalized coordinates vanishing to zero 16. 410: Eric Feron / MIT, Spring 2001

Slack variables (ct'd) 1 5 x 2 x 3 x 1 x 5 2 x 4 4 3 (2, 6) 16. 410: Eric Feron / MIT, Spring 2001

Basic, nonbasic variables At the origin zero, these distances are zero: x 1=0 These are called nonbasic variables x 2=0 And the other distances are nonzero: x 3 = 4 These are called basic variables x 4 = 6 x 5=18 Consider now the point (2, 6) (numbered 3). At that point: x 4=0 These are the active constraints, nonbasic variables x 5=0 x 1=2 These are the nonactive constraints, basic variables x 2=6 x 3=2 16. 410: Eric Feron / MIT, Spring 2001

Simplex method, illustrated • Rewriting the original optimization problem with x 1, x 2, x 3, x 4, x 5 Maximize: Z=3 x 1+5 x 2 Subject to: x 1+x 3=4 x 2+x 4=6 (2, 6) 3 x 1+2 x 2+x 5=18 2 3 • Same (2, 6)-centric coordinates: x 4 • (0, 6)-centric coordinates problem Same problem x 4 Express x 1, x 2, x 3, Z as functions of (x 4, x 5) • A problem formulation that's well adapted x 5 Look at the cost function. Which decision Z=3 x 1+5(6 -x 4) Z=30+3 x 1 -5 x 4 4 Z=30+3 x 1 -5 x 4 (Z at (0, 6) is 30) x 1 to x 1+x 3=4 start from (0, 0): Can find out costof&course. x 3, variable has best marginal gain. x 2, x 1+x 3=4 (a) x 1 x 4, x 5 as a function of x 1, x 2 easily: "(0, 0)From (0, 6)-centric coordinates, we get (However that's only a heuristic. Picking x 1 x 4+x 2=6 x 2 (b) x 4+x 2=6 x 2 centric coordinates" would work too. ) 3 x 1+2(6 -x 4)+x 5=18 3 x 1 -2 x 4+x 5=6 1 5 (c) 3 x 1 -2 x 4+x 5=6 • Choice x 1=0 and x 2=0 are(ct'd) the current active • x 1=6/3+2/3 x 4 -x 5/3 of x 1 or x 2 constraints. x 2=6 -x 4 • We How can an weimprovement move x 2? That depends canfar obtain of Z by movingon x 1 the up. x 2, x 3, x 5 found easily as functions of x 1, x 4 x 3=4 -x 1=4 -6 -2/3 x 4+x 5/3 Let'sfartryup? to move from one of these How constraints! In ouraway case the constraint x 2=6 is New, (0, 6)-centric coordinates constraints: (a) says (b) says nothing, (c)Thus says 2=>so x 1 moves hit first 4, (that's easy to see). the new corner (x 1, x 4) new x 1>0 "natural axes" to 2 Z=30+3 x 1 -5 x 4 =>is somake x 4 becomes the newcoordinate nonbasic variable. –Either make and point –Or make x 2>0 x 1=0=30+6+2 x 4 -x 5 -5 x 4 (2, 6) is newone corner-point feasible solution. –the Which do we pick? x 4=0=36 -3 x 4 -x 5 • Cost at (2, 6) is 36 • There is no way to improve => So we're done. 16. 410: Eric Feron / MIT, Spring 2001

Your example Maximize Z=4 x 1+3 x 2+6 x 3 Subject to 3 x 1+x 2+3 x 3<=30 2 x 1+2 x 2+3 x 3<=40 x 1>=0, x 2>=0, x 3>=0 16. 410: Eric Feron / MIT, Spring 2001