Introduction to the Measurement of Interest Rate Risk

Introduction to the Measurement of Interest Rate Risk by Frank J. Fabozzi Power. Point Slides by David S. Krause, Ph. D. , Marquette University Copyright 2007 John Wiley & Sons, Inc. All rights reserved. Reproduction or translation of this work beyond that permitted in Section 117 of the 1976 United States Copyright Act without the express permission of the copyright owner is unlawful. Request for futher information should be addressed to the Permissions Department, John Wiley & Sons, Inc. The purchaser may make back-up copies for his/her own use only and not for distribution or resale. The Publisher assumes no responsibility for errors, omissions, or damages caused by the use of these programs or from the use of the information contained herein.

Chapter 7 Introduction to the Measurement of Interest Rates • Major learning outcomes: – Quantifying the amount of risk affected by changing interest rates – The two approaches to measuring interest rate risk: • Full valuation • Duration/convexity

Approaches to Measuring Interest Rate Risk • There are two approaches to measure interest rate risk: full valuation approach and duration/convexity approach.

Full Valuation Approach to Measuring Interest Rate Risk • The full valuation approach involves revaluing a bond position (every position in the case of a portfolio) for a scenario of interest rate changes. • The advantage of the full valuation approach is its accuracy with respect to interest rate exposure for a given interest rate change scenario— accurate relative to the valuation model used— but its disadvantage for a large portfolio is having to revalue each bond for each scenario.

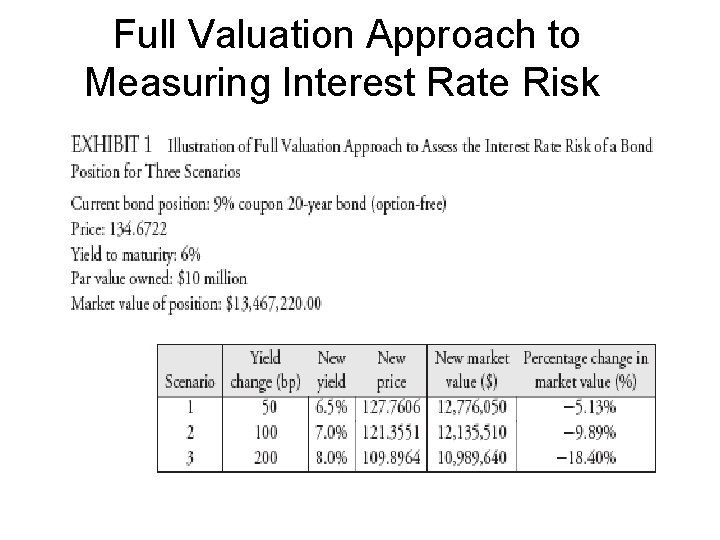
Full Valuation Approach to Measuring Interest Rate Risk • Exhibit 1 shows the most basic valuation approach to understanding the impact of changing interest rates for a bond portfolio. – It assumes a single interest rate for all periods (remember that this method is only valid with a flat term structure; however, in this case it is easier to use and demonstrates the point about interest rate risk).

Full Valuation Approach to Measuring Interest Rate Risk

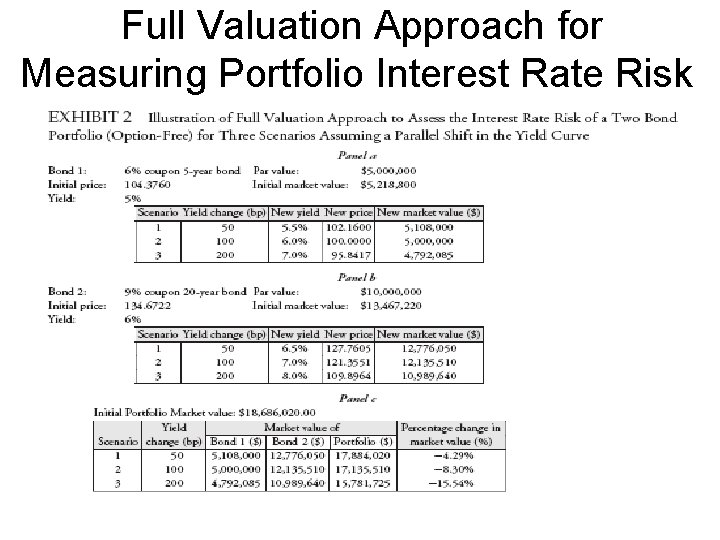
Full Valuation Approach for Measuring Portfolio Interest Rate Risk • Exhibit 2 shows the basic full valuation approach to changing interest rates for a bond portfolio with a parallel shift in the yield curve.

Full Valuation Approach for Measuring Portfolio Interest Rate Risk

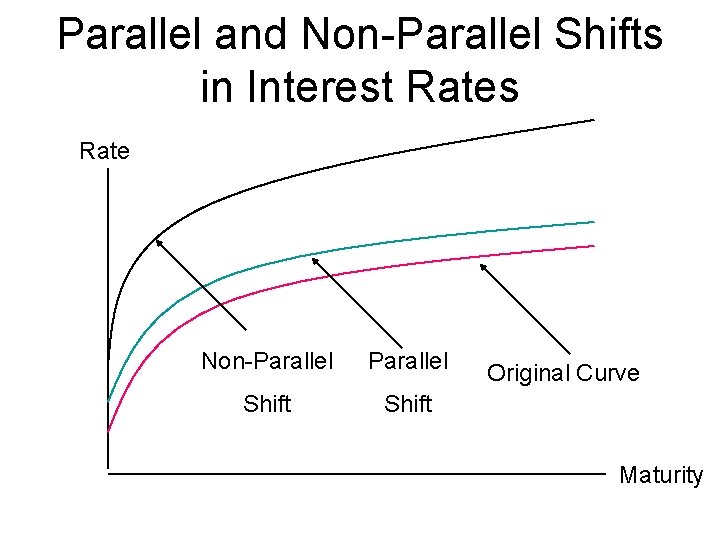
Parallel and Non-Parallel Shifts in Interest Rates Rate Non-Parallel Shift Original Curve Maturity

Full Valuation Approach for Interest Rate Risk (Non-Parallel Shift in Yields) • Exhibit 3 shows the basic full valuation approach to evaluating changing interest rates for a bond portfolio with a nonparallel shift in the yield curve. • This approach of examining the change in price and yield works fine; however, it is quite time consuming and it would be useful to have a single measure that could express the amount of interest rate risk for a single bond or a bond portfolio without having to compute the full valuation of each bond. – That’s where the duration measure plays a role.

Full Valuation Approach for Interest Rate Risk (Non-Parallel Shift in Yields)

Duration • Check spreadsheet

Bond Price/Yield Relationship • The characteristics of a bond that affect its price volatility are – (1) maturity, – (2) coupon rate, and – (3) presence of any embedded options. • The shape of the price/yield relationship for an option-free bond is convex. • The price sensitivity of a bond to changes in the required yield can be measured in terms of the dollar price change or percentage price change (Exhibit 4).

Bond Price/Yield Relationship

General Properties Concerning the Price Volatility of Option-Free Bonds 1. Although bond prices move in the opposite direction from the change in yield, the percentage price change is not the same for all bonds. 2. For small changes in yield, the percentage price change for a given bond is roughly the same, whether the yield increases or decreases. 3. For large changes in yield, the percentage change is not the same for an increase in yield as it is for a decrease in yield. 4. For a given large change in yield, the percentage price increase (with falling rates) is greater than the percentage price decrease (with increasing rates).

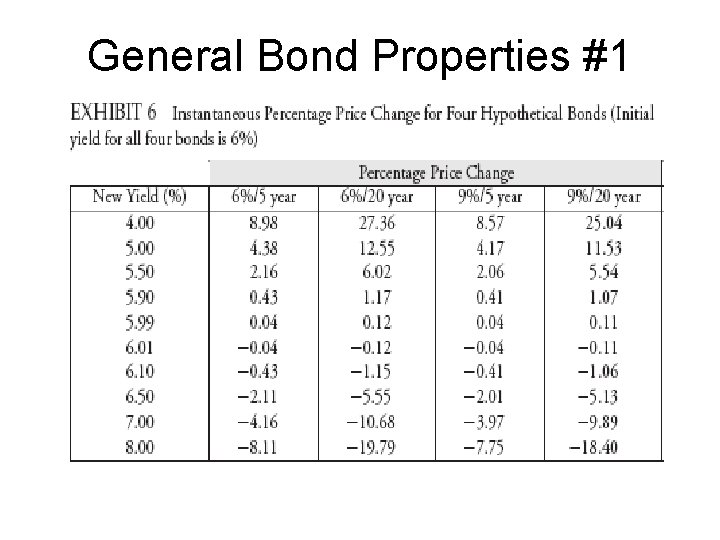
General Bond Properties • Property 1. In response to a given change in yield, the percentage change in the value of all bonds is not the same. – This is because the convexity of all bonds is not the same. – Longer maturity, for example, increases convexity. – Lower coupon increases convexity.

General Bond Properties #1

General Bond Properties (cont’d) • Property 2. For a very small change in the yield, the percentage gain and loss is approximately the same. – If the yield change is very close to the original yield, the price-volatility relationship is close to symmetric. – The curve is approximately symmetric close to any one point.

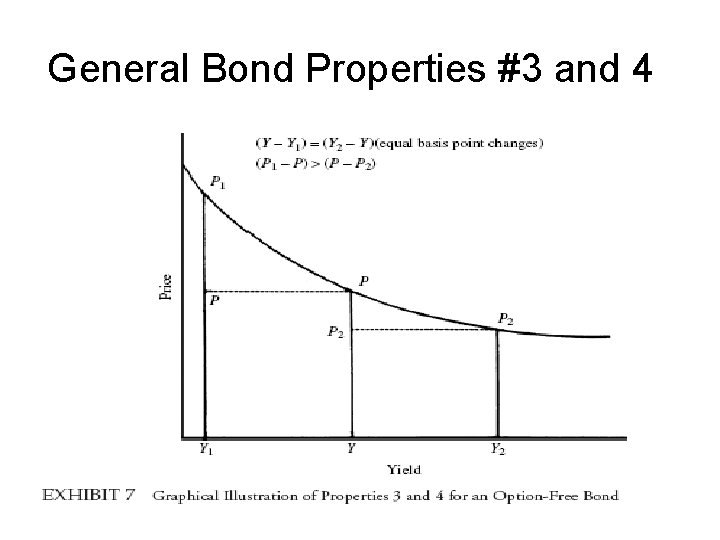
General Bond Properties (cont’d) • Property 3. For a large change in the yield, the percentage gain and loss is not the same. – Farther away from the original yield, the pricevolatility relationship is not symmetric. – The curve is not symmetric over a large range.

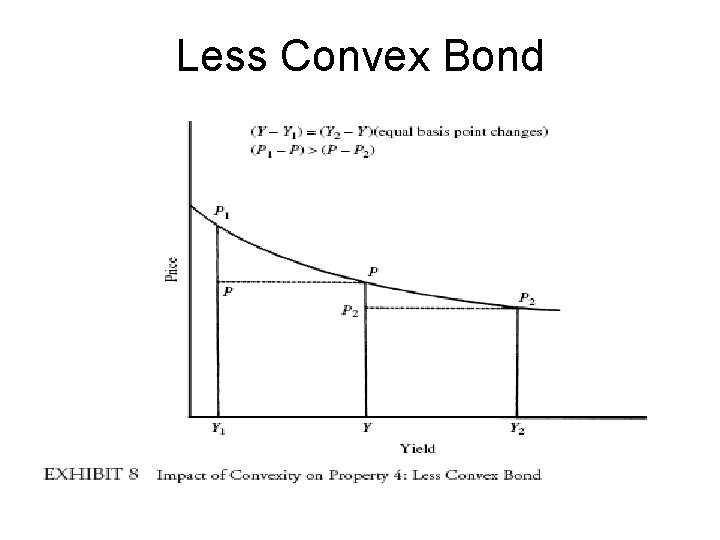
General Bond Properties (cont’d) • Property 4. For a given change in yield, the effect on price of a decrease in yield is greater than for an increase in yield. – If the yield goes down 1%, then the increase in price is greater than the decrease in price from the yield going up 1%. – The slope of the curve is ‘strictly’ increasing. – The convexity of the curve is the reason for this effect.

General Bond Properties #3 and 4

Less Convex Bond

Highly Convex Bond

General Bond Properties • The explanation for properties 3 and 4 come from the convex shape of the price/yield relationship. – As can be seen in the graph below, (Y 4 – Y 3) is a larger change in yield than (Y 2 – Y 1, ) yet the price change, (P 4 – P 3), is smaller than (P 2 – P 1).

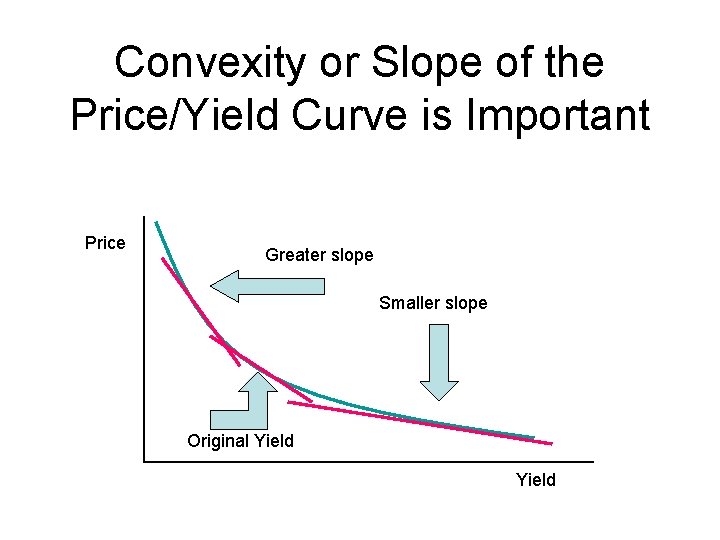
Logic Behind Properties 3 and 4 • As yield increases (decreases), the slope of the price/yield curve decreases (increases). • As yield increases, bond prices fall, but this is tempered by the decline in slope of the curve.

Convexity or Slope of the Price/Yield Curve is Important Price Greater slope Smaller slope Original Yield

Price Volatility of Bonds with Embedded Options • The price of a bond with an embedded option consists of two components: – Value of an option-free bond – Value of the embedded option • The most common types of embedded options are call (or prepay) options and put options. • Call bonds have a region of the price-yield relationship that displays negative convexity.

Price-Yield for a Callable Bond • Part 1: The price-yield for an option-free bond is convex: Price Yield

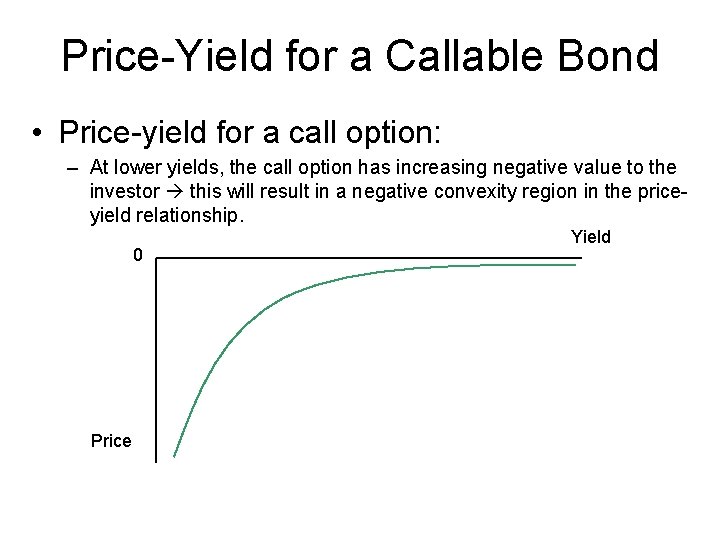
Price-Yield for a Callable Bond • Part 2: A call option has the following effects on the price of the option-free bond: – At high interest rates, the call option has almost no value (very unlikely to be exercised). • The price behaves at this point like an option-free bond – As interest rates decrease, the call option takes on negative value because it is more likely to be called. • The price behaves at this point differently than an option-free bond

Price-Yield for a Callable Bond • Price-yield for a call option: – At lower yields, the call option has increasing negative value to the investor this will result in a negative convexity region in the priceyield relationship. 0 Price Yield

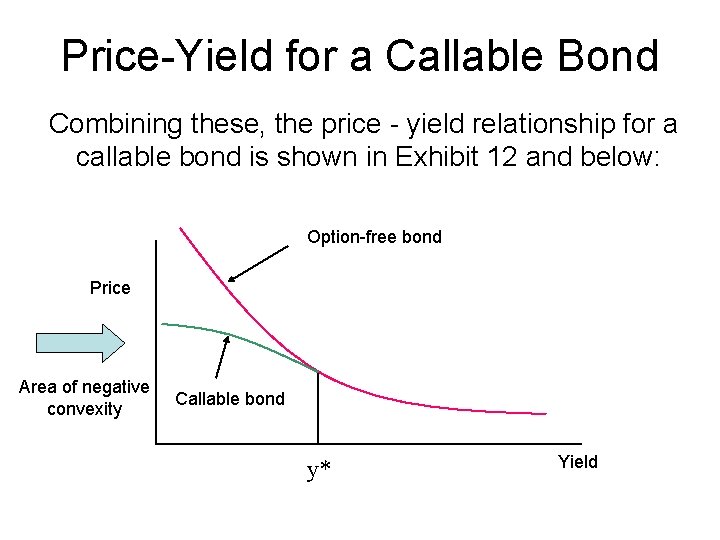
Price-Yield for a Callable Bond Combining these, the price - yield relationship for a callable bond is shown in Exhibit 12 and below: Option-free bond Price Area of negative convexity Callable bond y* Yield

Price-Yield for a Callable Bond • At high interest rates, the prices of callable and option-free bonds are approximately the same. • As interest rates decrease, the price of a callable bond increases at a slower rate than does an option-free bond, due to the increasing negative value of the call option.

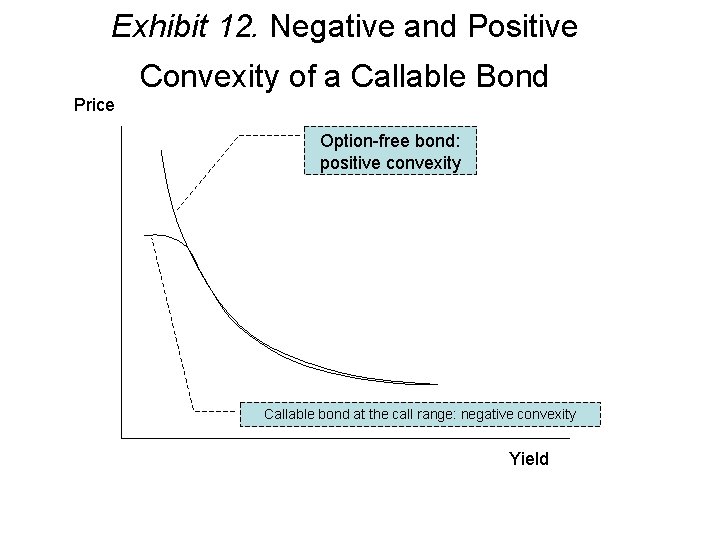
Convexity for a Callable Bond • ‘‘Negative convexity’’ means that for a large change in interest rates, the amount of the price appreciation is less than the amount of the price depreciation. – Option-free bonds exhibit positive convexity. • ‘‘Positive convexity’’ means that for a large change in interest rates, the amount of the price appreciation is greater than the amount of the price depreciation. • A callable bond exhibits positive convexity at high yield levels and negative convexity at low yield levels where ‘‘high’’ and ‘‘low’’ yield levels are relative to the issue’s coupon rate. • At low yield levels (low relative to the issue’s coupon rate), the price of a putable bond is basically the same as the price of an option-free bond because the value of the put option is small; as rates rise, the price of a putable bond declines, but the price decline is less than that for an option-free bond.

Price-Yield for a Callable Bond • Convexity – Option-free bonds have positive convexity through their range – Below y* (in Exhibit 12) callable bonds have negative convexity • This means that (contrary to an option-free bond) the absolute change in price is less as interest rates decline than when they rise.

Exhibit 12. Negative and Positive Convexity of a Callable Bond Price Option-free bond: positive convexity Callable bond at the call range: negative convexity Yield

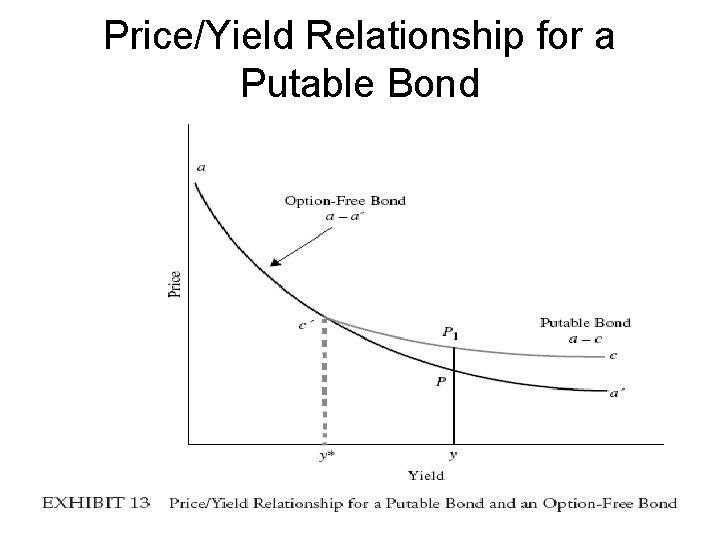
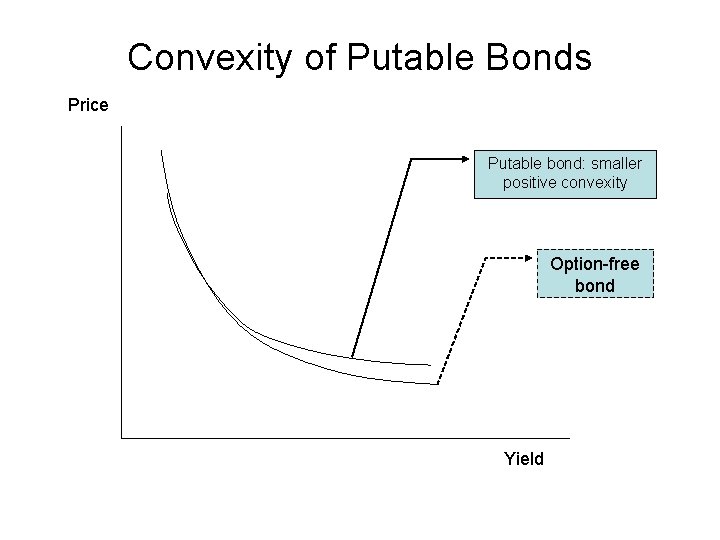
Valuing a Callable or Putable Bond • A great advantage in analyzing bonds with embedded options is that it is possible to separate the value and characteristics of the bond from those of the option. • Callable (putable) bond price = straight bond price –(+) call (put) option price • Putable bonds have a lower positive convexity than an option-free bond

Price/Yield Relationship for a Putable Bond

Convexity of Putable Bonds Price Putable bond: smaller positive convexity Option-free bond Yield

Convexity of Mortgage-Backed Bonds Price Higher prepayment risk at low interest: negative convexity Lesser prepayment hence “extension” risk: negative convexity Mortgaged-backed bonds Yield

Duration – The Other Approach to Analyzing Bond Price Volatility • Duration is measure of the approximate price sensitivity of a bond to interest rate changes. – It is the approximate percentage change in price for a 100 basis point change in interest rates. • It is the first (linear) approximation of the percentage price change. • To improve the duration approximation, an adjustment for “convexity” will be made. This is known as the duration/convexity approach.

Calculating Duration Fabozzi’s Equation (1) • Duration = (V- - V+) / 2(V 0)(Δy) – Where • Δy = change in yield in decimal • V 0 = initial price • V- = price if yields decline by Δy • V+ = price if yields increase by Δy – Example • Δy =. 002, V 0 = 134. 6722, V- = 137. 5888, and V+ = 131. 8439 • Duration = (137. 5888 – 131. 8439)/2(134. 6722)(. 002) = 10. 66

Duration • Duration - It can be thought of as the price sensitivity of a bond (or a portfolio of bonds) to changes in interest rates. • A zero coupon bond that matures in n years has a duration of n years • A coupon bearing bond maturing in n years has a duration of less than n years, because the holder receives some of the cash payments prior to year n.

Duration • Duration is a first approximation of a bond’s price or a portfolio’s value to interest rate changes. • To improve the estimate provided by duration, a convexity adjustment can be used. • Using duration combined with a convexity adjustment to estimate the percentage price change of a bond to changes in interest rates is called the duration/convexity approach to interest rate risk measurement. • Duration does a good job of estimating the percentage price change for a small change in interest rates but the estimation becomes poorer the larger the change in interest rates.

Duration for Bonds with Embedded Options • For bonds with embedded options, the problem with using a small shock to estimate duration is that divergences between actual and estimated price changes are magnified by dividing by a small change in rate in the denominator of the duration formula; in addition, small rate shocks that do not reflect the types of rate changes that may occur in the market do not permit the determination of how prices can change because expected cash flows may change. • For bonds with embedded options, if large rate shocks are used the asymmetry caused by convexity is encountered; in addition, large rate shocks may cause dramatic changes in the expected cash flows for bonds with embedded options that may be far different from how the expected cash flows will change for smaller rate shocks.

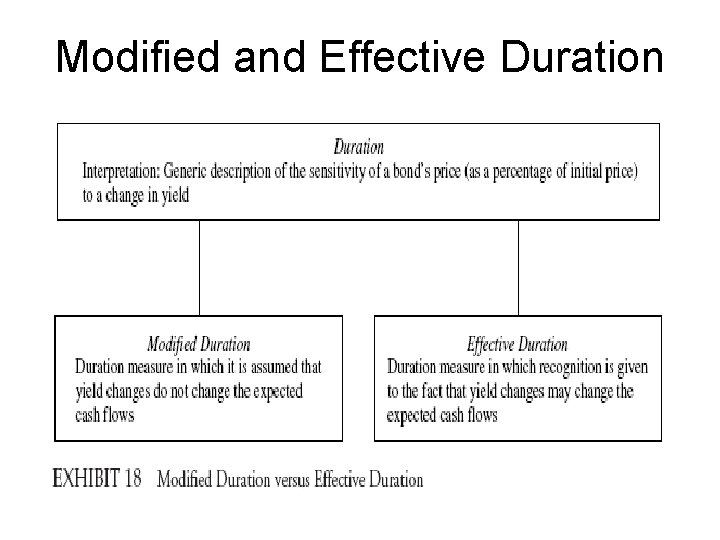
Modified and Effective Duration • Modified duration is the approximate percentage change in a bond’s price for a 100 basis point change in yield assuming that the bond’s expected cash flows do not change when the yield changes. • In calculating the values to be used in the numerator of the duration formula, for modified duration the cash flows are not assumed to change and therefore, the change in the bond’s price when the yield is changed is due solely to discounting at the new yield levels. • Effective duration is the approximate percentage change in a bond’s price for a 100 basis point change in yield assuming that the bond’s expected cash flows do change when the yield changes. • Modified duration is appropriate for option-free bonds; effective duration should be used for bonds with embedded options.

Modified and Effective Duration

Modified and Effective Duration • The difference between modified duration and effective duration for bonds with an embedded option can be quite dramatic. • Macaulay duration is mathematically related to modified duration and is therefore a flawed measure of the duration of a bond with an embedded option. • Interpretations of duration in temporal terms (i. e. , some measure of time) or calculus terms (i. e. , first derivative of the price/yield relationship) are operationally meaningless and should be avoided.

Error in Estimating Price Based on Duration Only Price Error in estimating price based only on duration Actual Price Error Tangent line R 0 Yield

Implications of Tangent Line Duration Approximation • Duration is good for estimating the impact of small interest rate changes. • It is not as accurate for large interest rate movements. • The duration estimate is less accurate, the more convex the bond price/yield relationship. • The tangent line (duration approximation) always underestimates the actual price. • This only works for option-free bonds.

Interpretation of Duration • Don’t make this out to be ‘rocket science’ – While duration is the first derivative of the bond’s price/yield function, it is simply a measure of the approximate percentage price change for a 100 basic point change in interest rates. • It is possible for two bonds to have the same duration, but different convexity and to behave differently across large interest rate changes.

Portfolio Duration • The duration for a portfolio is equal to the market-value weighted duration of each bond in the portfolio. • In applying portfolio duration to estimate the sensitivity of a portfolio to changes in interest rates, it is assumed that the yield for all bonds in the portfolio change by the same amount. • The duration measure indicates that regardless of whether interest rates increase or decrease, the approximate percentage price change is the same; however, this is not a property of a bond’s price volatility for large changes in yield.

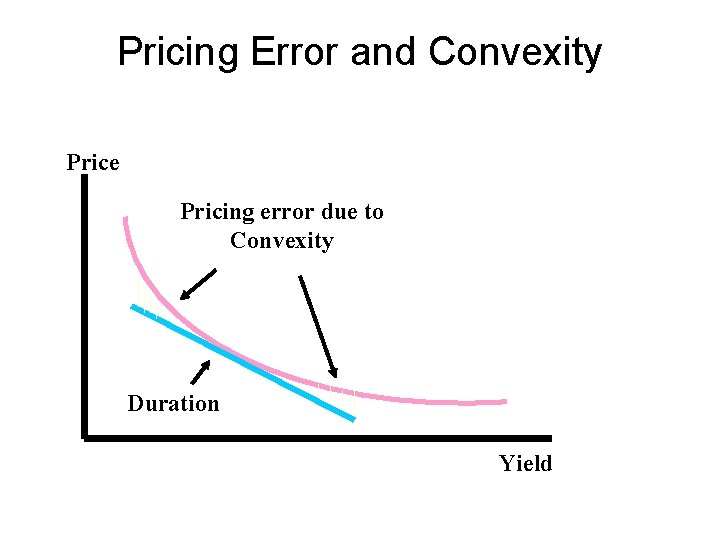
Convexity • None of the previous price-volatility measures capture the non-linearity or curvature of that relationship. – These measures are only approximate. – These measure are only good locally. • We need an additional factor to capture the curvature of the relationship.

Pricing Error and Convexity Price Pricing error due to Convexity Duration Yield

Convexity Adjustment • A convexity adjustment can be used to improve the estimate of the percentage price change obtained using duration, particularly for a large change in yield. • The convexity adjustment is the amount that should be added to the duration estimate for the percentage price change in order to obtain a better estimate for the percentage price change. • The same distinction made between modified duration and effective duration applies to modified convexity adjustment and effective convexity adjustment.

Convexity Adjustment for a Bond with an Embedded Option • For a bond with an embedded option that exhibits negative convexity at some yield level, the convexity adjustment will be negative.

Convexity Adjustment • The formula for the convexity adjustment to the percentage price change is: C times (change in the yield) squared times 100 C x (Δy)2 x 100 • Where C is the change in price not explained by duration • Remember that: Duration = (V- - V+) / 2(V 0)(Δy) – Where Δy = change in yield in decimal V 0 = initial price V- = price if yields decline by Δy V+ = price if yields increase by Δy

Calculating Convexity for a 200 Basis Point Change • C = (V- + V+ - 2(V 0)) / 2(V 0) (Δy)2 – Where • • Δy = change in yield in decimal V 0 = initial price V- = price if yields decline by Δy V+ = price if yields increase by Δy – Example • Δy =. 002, V 0 = 134. 6722, V- = 137. 5888, and V+ = 131. 8439 • C = (131. 8439 +137. 5888 – 2 (134. 6722) / 2(134. 6722)(. 002)2 = 81. 95 • Convexity Adjustment = 81. 95 x (. 002)^2 x 100 = 3. 28%

Calculating Duration for a 200 Basis Point Change • Duration = (V- - V+) / 2(V 0)(Δy) – Where • • Δy = change in yield in decimal V 0 = initial price V- = price if yields decline by Δy V+ = price if yields increase by Δy – Example • Δy =. 002, V 0 = 134. 6722, V- = 137. 5888, and V+ = 131. 8439 • Duration = (137. 5888 – 131. 8439)/2(134. 6722)(. 002) = 10. 66 • 200 basis point change would be: – 2 x 10. 66 / 100 = -21. 32%

Calculating the Price Change for a 200 Basis Point Change • Estimated change for a yield going from 6% to 4%: – Estimated change using duration = -21. 32% – Convexity adjustment = +3. 28% – Total est. percentage change = -18. 04% • Estimated change for a yield going from 4% to 6%: – Estimated change using duration = +21. 32% – Convexity adjustment = +3. 28% – Total est. percentage change = +24. 60%

Price Value of a Basis Point Change • The price value of a basis point (or dollar value of an 01) is the change in the price of a bond for a 1 basis point change in yield. • The price value of a basis point is the same as the estimated dollar price change using duration for a 1 basis point change in yield.

Yield Volatility • Yield volatility must be recognized in estimating the interest rate risk of a bond a portfolio. • Value-at-risk is a measure that ties together the duration of a bond and yield volatility.