Introduction to the Hankel based model order reduction

Introduction to the Hankel -based model order reduction for linear systems D. Vasilyev Massachusetts Institute of Technology, 2004

State-space description MIMO LTI CT dynamical system: Here we assume a system to be stable, i. e matrix A is Hurwitz.

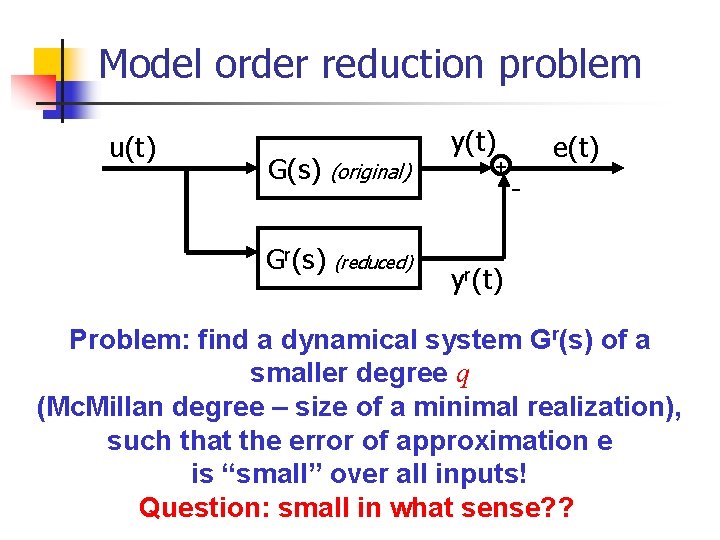
Model order reduction problem u(t) y(t) G(s) (original) Gr(s) (reduced) + e(t) - yr(t) Problem: find a dynamical system Gr(s) of a smaller degree q (Mc. Millan degree – size of a minimal realization), such that the error of approximation e is “small” over all inputs! Question: small in what sense? ?

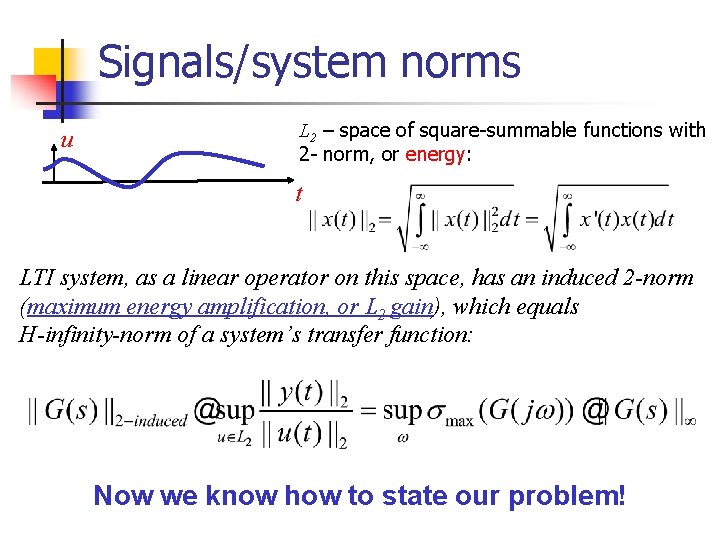
Signals/system norms u L 2 – space of square-summable functions with 2 - norm, or energy: t LTI system, as a linear operator on this space, has an induced 2 -norm (maximum energy amplification, or L 2 gain), which equals H-infinity-norm of a system’s transfer function: Now we know how to state our problem!

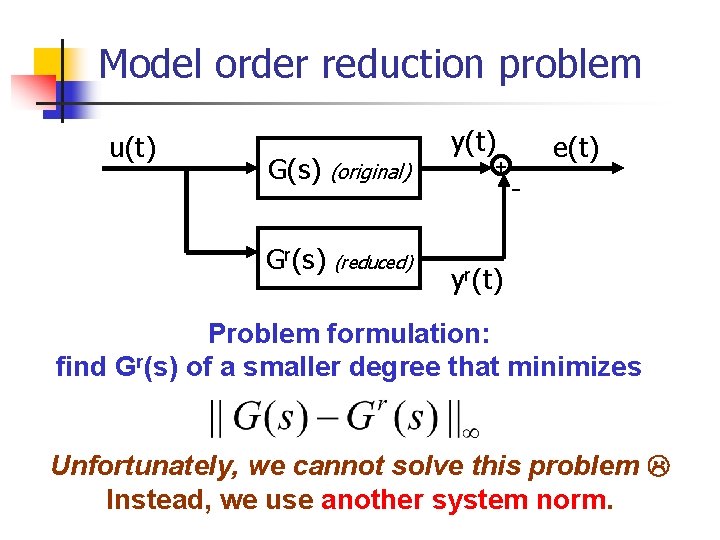
Model order reduction problem u(t) y(t) G(s) (original) Gr(s) (reduced) + e(t) - yr(t) Problem formulation: find Gr(s) of a smaller degree that minimizes Unfortunately, we cannot solve this problem Instead, we use another system norm.

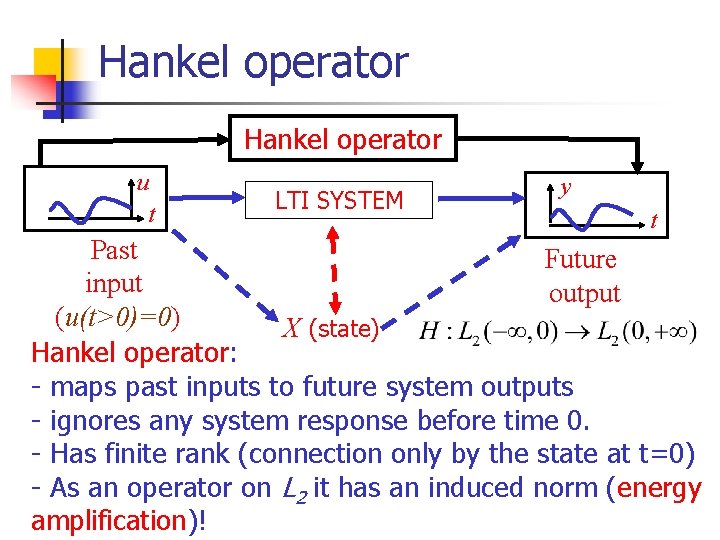
Hankel operator u t LTI SYSTEM y t Past Future input output (u(t>0)=0) X (state) Hankel operator: - maps past inputs to future system outputs - ignores any system response before time 0. - Has finite rank (connection only by the state at t=0) - As an operator on L 2 it has an induced norm (energy amplification)!

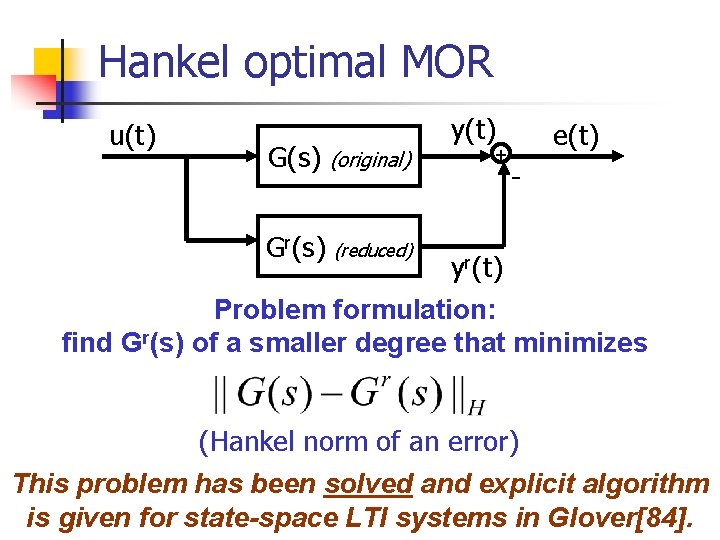
Hankel optimal MOR u(t) y(t) G(s) (original) Gr(s) (reduced) + e(t) - yr(t) Problem formulation: find Gr(s) of a smaller degree that minimizes (Hankel norm of an error) This problem has been solved and explicit algorithm is given for state-space LTI systems in Glover[84].

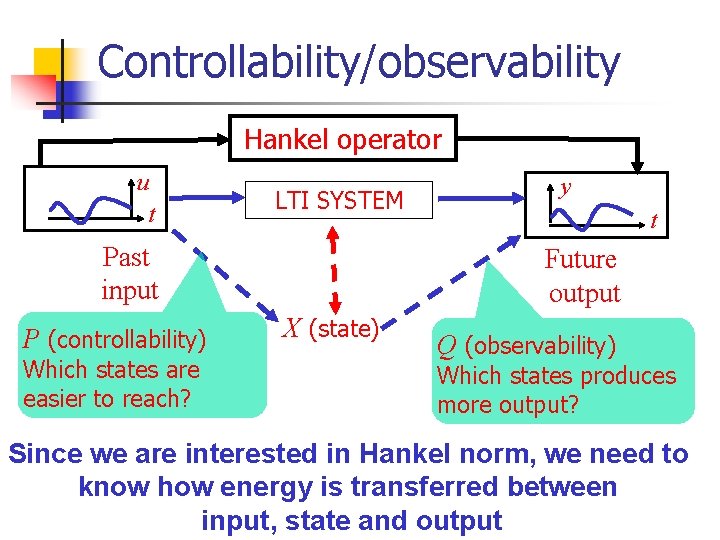
Controllability/observability Hankel operator u t LTI SYSTEM Past input P (controllability) Which states are easier to reach? y t Future output X (state) Q (observability) Which states produces more output? Since we are interested in Hankel norm, we need to know how energy is transferred between input, state and output

Observability X(0) y t Future output How much energy in the output we shall observe if the system is released from some state x(0)? Observability Gramian ATQ +QA = -CTC Satisfies Lyapunov Q is SPD iff system is observable equation:

Controllability Past input u t X(0) State What is the minimal energy of input signal needed to drive system to the state x(0)? Controllability Gramian AP + PAT = -BBT Satisfies Lyapunov equation: P is SPD iff system is controllable

Side note about Lyapunov equations AP + PA′ = -R, R - hermitian This equation has a unique solution P=P′ if and only if: Moreover, if R is SPD and A is Hurwitz, then P is SPD. Assume some LTI CT system: Lyapunov function: V(x)=x’Px >0 (reformulation of stability criterion)

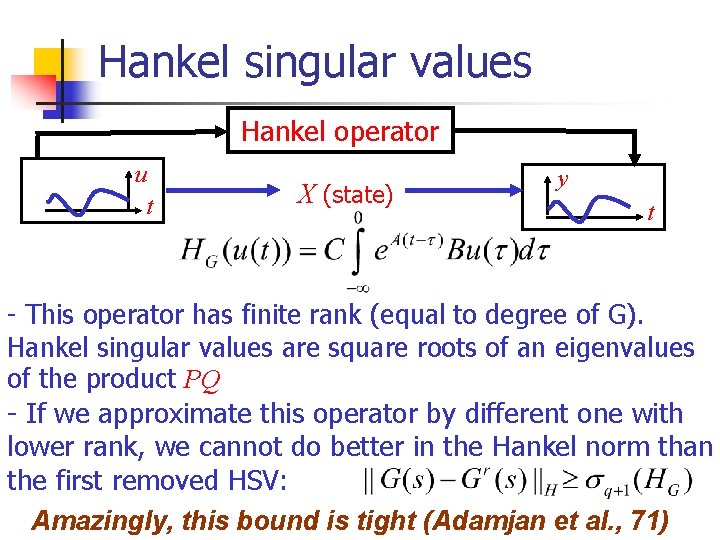
Hankel singular values Hankel operator u t X (state) y t - This operator has finite rank (equal to degree of G). Hankel singular values are square roots of an eigenvalues of the product PQ - If we approximate this operator by different one with lower rank, we cannot do better in the Hankel norm than the first removed HSV: Amazingly, this bound is tight (Adamjan et al. , 71)

Truncated balanced reduction Gramians are transformed with the change of basis as a quadratic forms: x → Tx, P → TPTT, Q → T-TQT-1 We can find a basis, in which both gramians are equal and diagonal. Such transformation is called balancing transformation. P = R TR UΣ 2 UT = RQRT T = RTU Σ-1/2 P = Q = diag(σ1, … , σn), σ1 ≥ … ≥ σn

Truncated balanced reductioncont’d In the balanced realization we can perform truncation of the least observable and controllable modes! Truncated system (A 11, B 1, C 1, D) will be stable (if σq ≠ σq+1 , otherwise stable for almost all T ) and have the following H-infinity error bound: “twice sum of a tail” rule

Truncated balanced reduction vs. Hankel optimal reduction For the balanced truncation procedure we have the following error bounds: TBR is not optimal in terms of the Hankel norm! For the Hankel optimal MOR the following bounds hold:

References: n Keith Glover, “All optimal Hankel-norm approximations of linear multivariable systems and their L-infinity error bounds”