Introduction to the displacement method l Displacement method

§ Introduction to the displacement method l. Displacement method l. Element stiffness matrix of 1 D spring l. Assembly of system equation l. Boundary conditions (BC) l. Summary § Principle of minimum potential energy 1. Total potential energy，πp 2. Stationary value of a function G(x) 3. Principle of minimum potential energy 4. Derivation of element equation of a spring § TRUSSES l Definition l Element stiffness matrix of a rod under axial load l Transformation matrix and stiffness matrix in 2 D l Stress for a bar (truss) element in 2 D

§ Introduction to the displacement method l. Displacement method l Element stiffness matrix of ID spring l Assembly of system equation l Boundary conditions (BC) l Summary

§ Displacement method A finite element approach method was proposed in the early 1950 s for investigating the complex behavior of structural problems by considering the nodal displacements as the basic unknowns in the system of equations. Stiffness matrix nodal displacements (unknowns) Basic equations of the displacement method are derived from (1) The equilibrium of nodal forces (2) The compatibility of displacements (3) The force-displacement relationship

§ Element stiffness matrix of ID spring by displacement method (1) Element stiffness matrix (2) Spring under axial load (3) Procedures of derivation of stiffness matrix

(1) Element stiffness matrix An element stiffness matrix relates element nodal forces and nodal displacements by

(2) Spring under axial load Consider a linear spring with spring constant K and length L under axial load. Positive x direction i, j：nodal number , ： nodal displacements at nodal i and j , ：nodal forces at nodal i and j

(3) Procedures (A) Satisfy static equilibrium (B) Relate the compatibility of displacements (C) Relate force to displacement (D) Derivation of element stiffness matrix

(A) Satisfy the static equilibrium or (1) (B) Relate the compatibility of displacements Assume that the spring has a total elongation δ due to the tensile force. (2)

(C) Relate force to displacement For the linear spring , tensile force and elongation are related through Hooke´s law by (3)

(D) Derivation of element stiffness matrix By the sign convection for nodal force , we have (4) Using Esq. . (2), (3), (4), we have or In matrix form Two linear Eqns. with two unknowns or where =element stiffness matrix (local) =vector of nodal forces =vector of nodal displacement

§ Assembly of system equation ：Internal forces ：External forces Element 2 Element 1 local node global node i 1 i 3 j 2

§ Assembly of system equation Augmented stiffness equations (Expand the element matrix to the order of the total stiffness matrix) Element 1 Element 2

§ Assembly of system equation Nodal force equilibrium equation (每個node的力需平衡) Compatibility (continuity)equation

§ Assembly of system equation Assembly Imposed equilibrium and compatibility on global level ：global nodal force matrix ：global stiffness matrix ：global displacement matrix

§ Assembly of system equation l Direct stiffness method A reliable method directly assembles individual element stiffness matrix to form the global stiffness matrix and global system equations. l Direct assembly of DSM According to the D. O. F. (short cut)

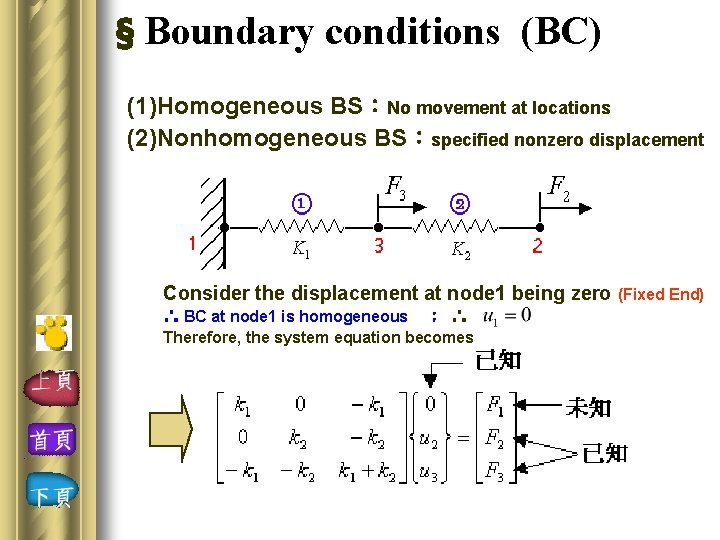
§ Boundary conditions (BC) (1)Homogeneous BS：No movement at locations (2)Nonhomogeneous BS：specified nonzero displacement Consider the displacement at node 1 being zero ∴ BC at node 1 is homogeneous ； ∴ Therefore, the system equation becomes (Fixed End)

§ Boundary conditions (BC) Because u 1 = 0, so column 1 has no effects on {F}ext. By directly deleting the row and column of above system equation corresponding to the zero-displacement d. o. f. , the equation reduces to Two Eqns for two unknowns Solve above Eq. for displacements u 2 and u 3. Reaction force F 1

§ Boundary conditions (BC) Element force on each spring element:

§ Boundary conditions (BC) Now, consider the case of nonhomogeneous boundary conditions. Assume u 1 = δ, where δ is a known displacement. Thus system equation becomes Rewrite above Eq. in expanded form. Considering the 2 nd and 3 rd terms of above eq and transforming the known δ terms to the right side, we have

§ Summary (1) Define analysis problem : ID linear spring (2) Constitutive equation F=ku (3) Form element stiffness matrix (4) Form system equation

§ Summary (5)Apply load/boundary conditions (6) Solve the system equation (a) Obtain nodal displacements (b) Obtain element forces

§ Principle of minimum potential energy 1. Total potential energy，πp 2. Stationary value of a function G(x) 3. Principle of minimum potential energy 4. Derivation of element equation of a spring

1. Total potential energy，πp Where U = Internal strain energy V= Potential energy of external forces Strain energy The capacity of internal forces (or stresses ) to do work through deformation (strain) in the structure. Potential energy The capacity of body forces, surface traction forces and applied nodal forces to do work through deformation of the structure. Total strain energy of the spring Potential energy of external force of the spring

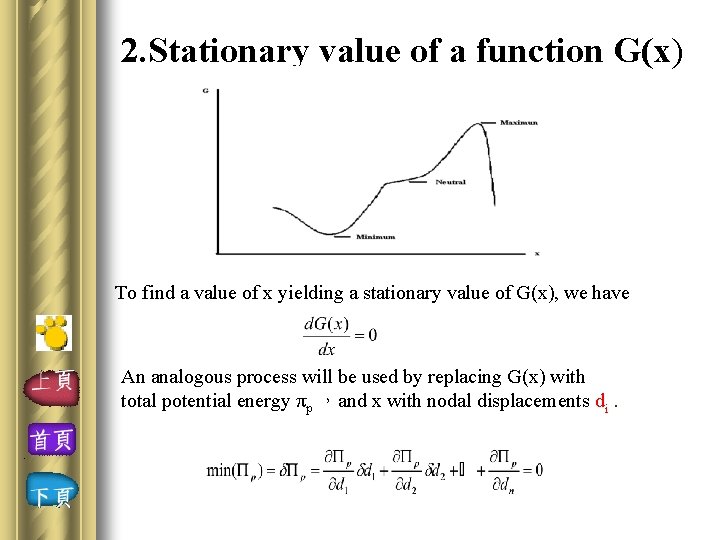
2. Stationary value of a function G(x) To find a value of x yielding a stationary value of G(x), we have An analogous process will be used by replacing G(x) with total potential energy πp ，and x with nodal displacements di.

3. Principle of minimum potential energy The principle states that equilibrium exits when the nodal displacement di defines a structure state such that for arbitrary admissible variations δdi from the equilibrium state. δdi might be nonzero. Hence, to satisfy dπp =0, all coefficients associated with δdi must be zero independently. Thus i=1. 2. ‥n where n equations must be solved for n values of the di that define the static equilibrium state of the structure.

4. Derivation of element equation of a spring Min (Πp)=0 or In matrix form

§ TRUSSES l Definition l Element stiffness matrix of a rod under axial load l Transformation matrix and stiffness matrix in 2 D l Stress for a bar (truss) element in 2 D

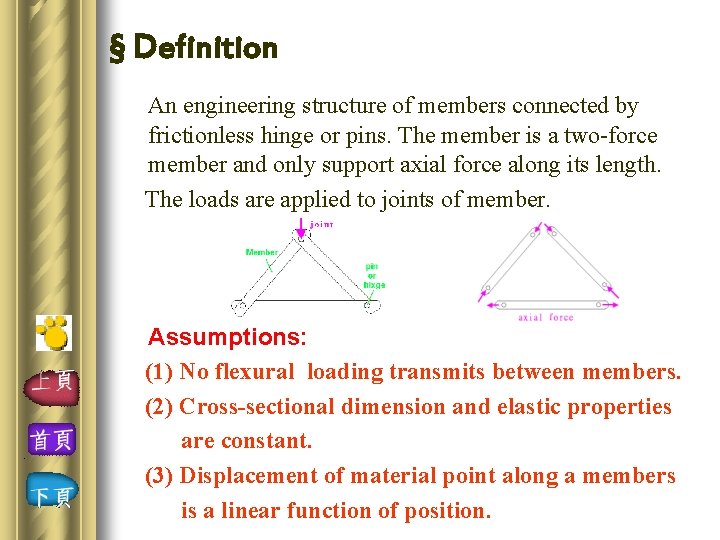
§ Definition An engineering structure of members connected by frictionless hinge or pins. The member is a two-force member and only support axial force along its length. The loads are applied to joints of member. Assumptions: (1) No flexural loading transmits between members. (2) Cross-sectional dimension and elastic properties are constant. (3) Displacement of material point along a members is a linear function of position.

§ Element stiffness matrix of a rod element Consider a rod (truss) element under axial load as shown. Here, the rod element is assumed to have constant cress-sectional area A, elastic constant E, and initial length L. u 1, u 2 = axial displacements at nodes 1 and 2. f 1, f 2 = axial nodal forces at nodes 1 and 2.

§ Element stiffness matrix of a rod element Steps for derivation of the stiffness matrix for the rod element: A. Force equilibrium B. B. Strain/Displacement relation l l Assume strain is constant in element Assume that elongation of the rod due to axial load is △L C. Stress/Strain law l l Assume that a homogenous, isotropic material Hooke’s law (Axial stress = P/A)

§ Element stiffness matrix of a rod element D. Relate force to stress E. Relate force to displacement F. Substitute Eqs. (2) & (3) into Eq (4) to yield Matrix form Element stiffness matrix Note: AE/L for a rod element is analogous to the spring constant k for a spring element.

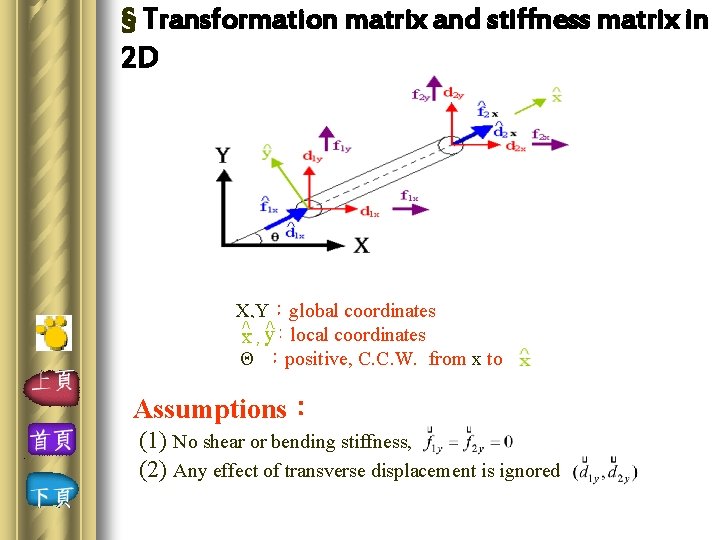
§ Transformation matrix and stiffness matrix in 2 D X, Y：global coordinates ：local coordinates Θ ：positive, C. C. W. from x to Assumptions： (1) No shear or bending stiffness, (2) Any effect of transverse displacement is ignored

§ Transformation matrix and stiffness matrix in 2 D Rod element equation in the local coordinate system In the global coordinate system XY

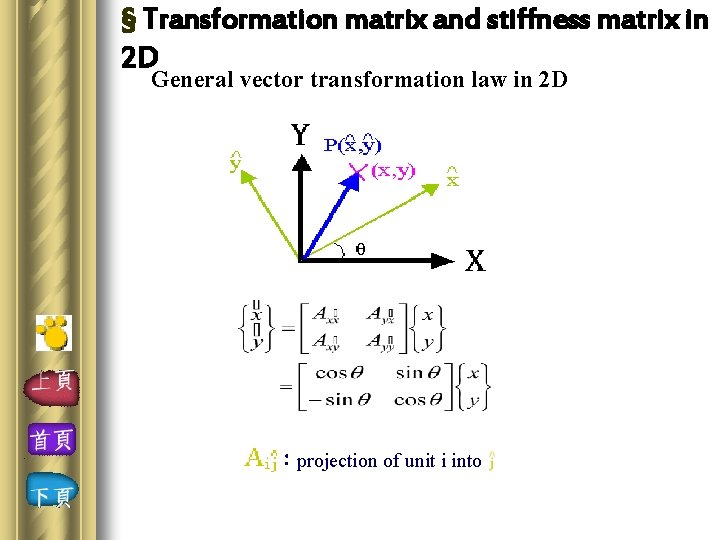
§ Transformation matrix and stiffness matrix in 2 D General vector transformation law in 2 D ：projection of unit i into

§ Transformation matrix and stiffness matrix in 2 D Hence, the relation between the global displacement � d� and the local displacement is Similarly Expand to the order of the global coordinates.

§ Transformation matrix and stiffness matrix in 2 D Similarly Premultiply both sides by

§ Transformation matrix and stiffness matrix in 2 D (For orthogonal matrix) Hence, the global stiffness matrix for an 2 D rod element is Total stiffness matrix and force matrix are System equation is

§ Stress for a rod (truss) element in 2 D Local force/local displacement relation is

§ Stiffness matrix for a rod element in 3 D The global stiffness matrix for an 3 D rod element is Symm. Where Cx = cosqx, Cy = cosqy and Cz = cosqz.