Introduction to the Design and Analysis of Algorithms

Introduction to the Design and Analysis of Algorithms El. Sayed Badr Benha University September 20, 2016

Exercise 1: Consider the following algorithm for finding the distance between the two closest elements in an array of numbers. ALGORITHM Min. Distance(A[0. . n − 1]) //Input: Array A[0. . n − 1] of numbers //Output: Minimum distance between two of its elements dmin←∞ for i ← 0 to n − 1 do for j ← 0 to n − 1 do if i = j and |A[i]− A[j ]| < dmin ←|A[i]− A[j ]| return dmin Make as many improvements as you can in this algorithmic solution to the problem. If you need to, you may change the algorithm altogether; if not, improve the implementation given 2

Exercise 1: 1 - We can sort and then determine the difference between two consecutive numbers and search about minimum distance O(n log n ) + O(n/2)+ O(n)= O(n log n ). 2 - We can use the similarity of the matrix. ( Ineer loop ). 3

Two main issues related to algorithms • How to design algorithms • How to analyze algorithm efficiency

Analysis of algorithms • How good is the algorithm? – time efficiency – space efficiency – correctness ignored in this course • Does there exist a better algorithm? – lower bounds – optimality 1 -5

• Algorithm: A well-defined computational procedure (namely, a sequence of elementary computational steps) which takes an input value and produces an output value, according to a special mathematical function. • Describing algorithms: pseudocode • • Pseudocode example input: integers a, b output: a × b sum 0 for j 1 to b do sum + a return sum • Pseudocode conventions – indention indicates block structure – while/for/repeat/if/then/else – loop counters retain values !!! – ** or. comment – variables are local (unless stated otherwise) – parameters passed by value – comparison: boolean “short circuit” evaluation e. g. j > 0 AND A[j] < key

Example: We try to search about value x in the following array : 1 n Best case : If A[1] = x T(n) = 1 O (1) x Worst case : If A[n] = x T(n) = n O (n) x Worst case : If A[n/2] = x T(n) = n/2 x O (n/2)

Algorithms Complixty The running time T(n) of the algorithm depends on the number of instructions of this algorithm where n is the size of input. Example: int a = 4; T(n) =1 ; O(1). Example: int a = 4; Int b = 2; C=a+b; T(3) ; O(3) Sume = ; For(i=1; i<=n; i++ ){ Sum = sum + A(i); T(n) = 2 n+1 Cout<<sum } O(n)

Algorithms Complixty Example: Sume = ; For(i=1; i<=n; i++ ) For(j=1; j<=n; j++ ) Sum = sum + A(i); Cout<<sum } T(n) = 2 n 2+1 O(n 2)

• Correctness

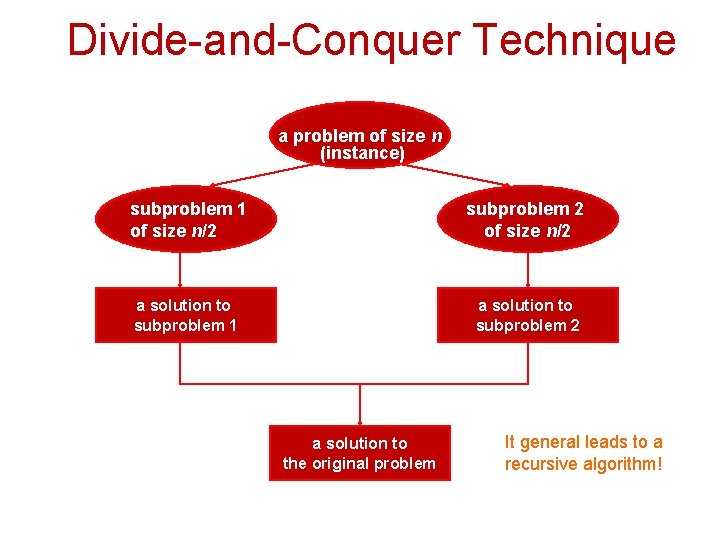
Divide-and-Conquer Technique The most-well known algorithm design strategy: 1. Divide instance of problem into two or more smaller instances 2. Solve smaller instances recursively 3. Obtain solution to original (larger) instance by combining these solutions

Divide-and-Conquer Technique a problem of size n (instance) subproblem 1 of size n/2 subproblem 2 of size n/2 a solution to subproblem 1 a solution to subproblem 2 a solution to the original problem It general leads to a recursive algorithm!

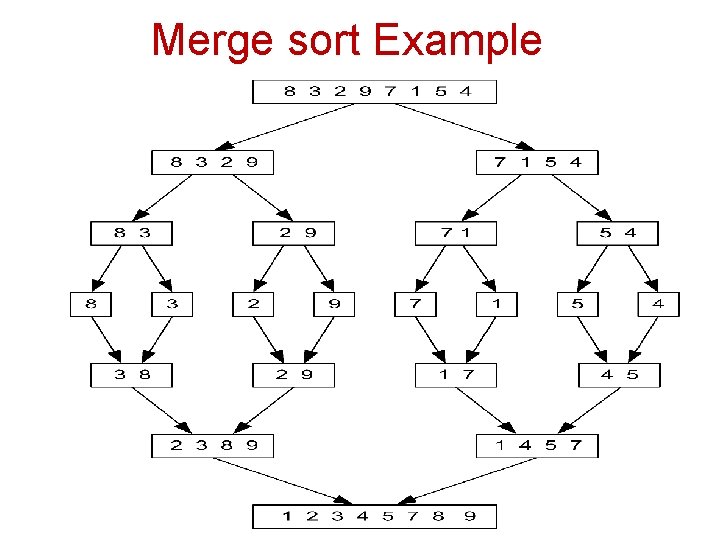
Merge sort Example

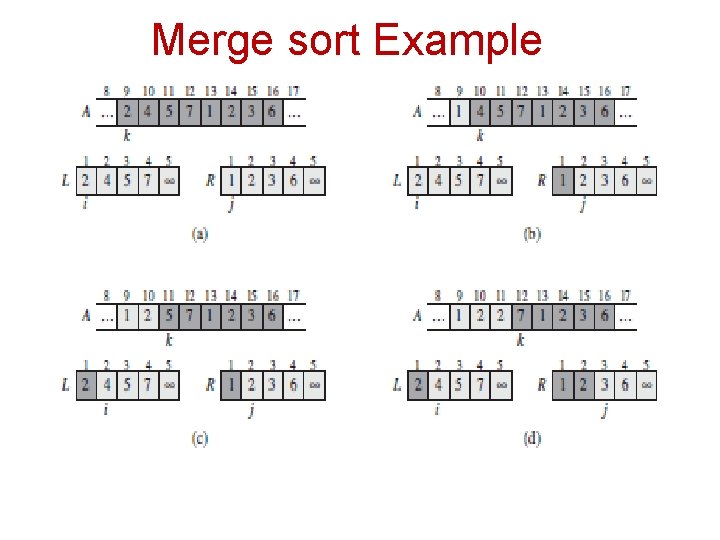
Merge sort Example

Merge sort Pesudocod

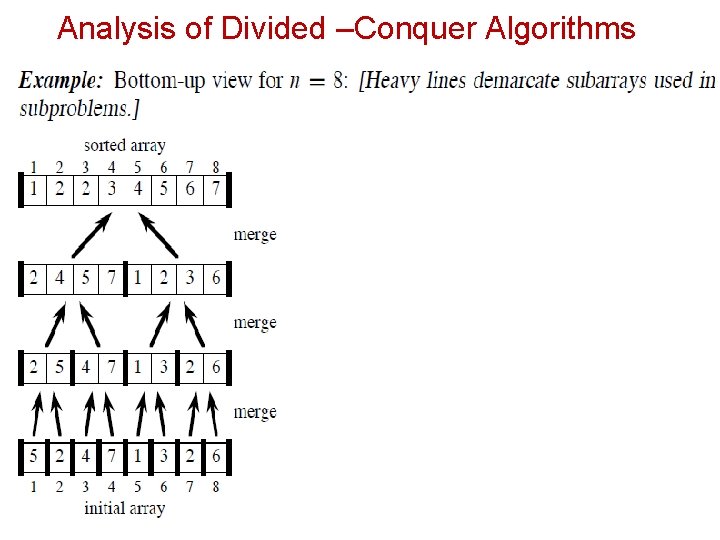
Analysis of Divided –Conquer Algorithms

Analysis of Divided –Conquer Algorithms