Introduction to tensor tensor factorization and its applications

Introduction to tensor, tensor factorization and its applications Mu Li i. PAL Group Meeting Sept. 17, 2010

Outline �Basic concepts about tensor 1. What’s tensor? Why tensor and tensor factorization? 2. Tensor multiplication 3. Tensor rank �Tensor factorization 1. CANDECOMP/PARAFAC factorization 2. Tucker factorization �Applications of tensor factorization �Conclusion

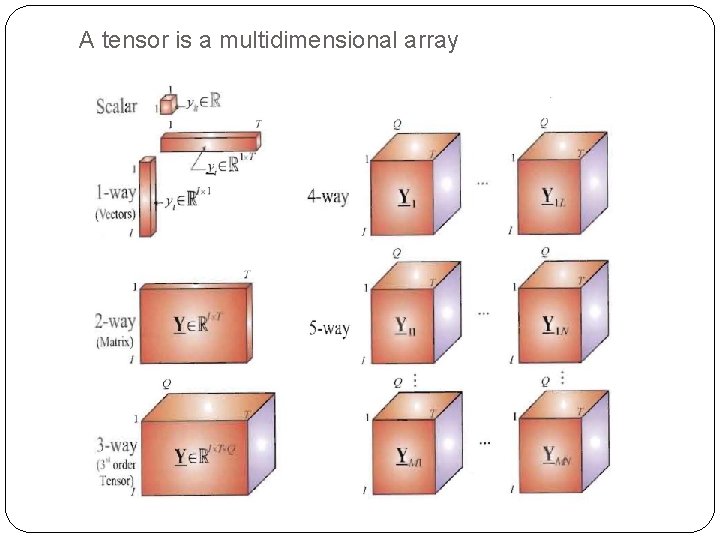
What’s tensor? Why tensor and tensor factorization? � Definition: a tensor is a multidimensional array which is an extension of matrix. � Tensor can happen in daily life. � In order to facilitate information mining from tensor and tensor processing, storage, tensor factorization is often needed. � Three-way tensor:

A tensor is a multidimensional array

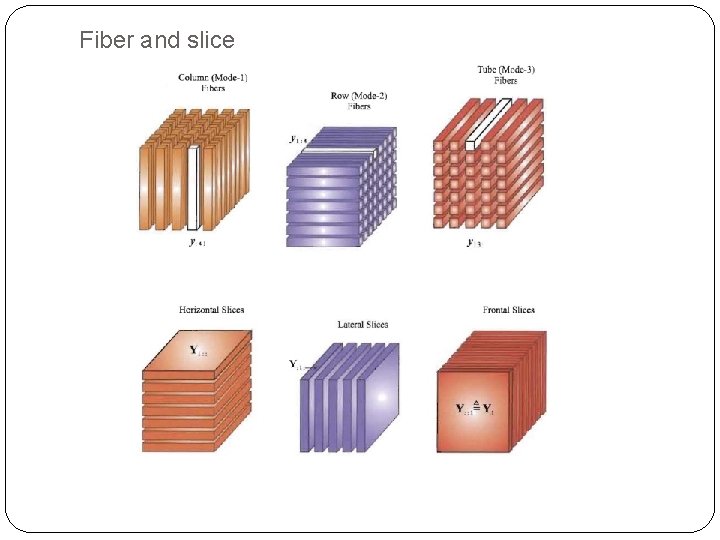
Fiber and slice

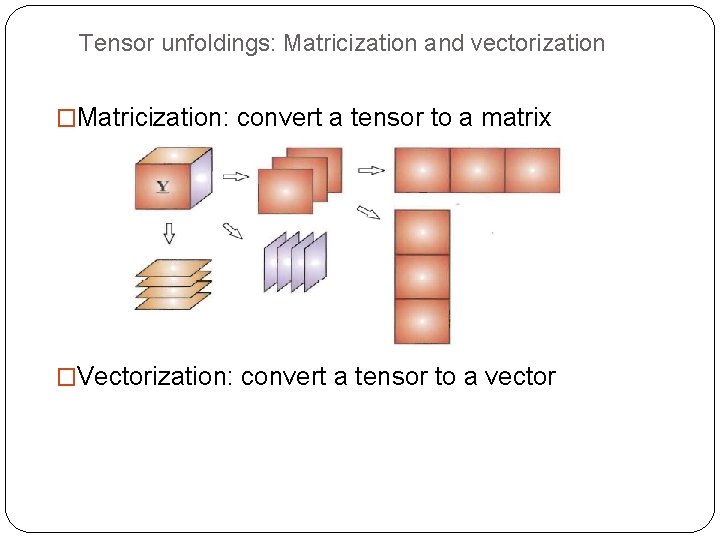
Tensor unfoldings: Matricization and vectorization �Matricization: convert a tensor to a matrix �Vectorization: convert a tensor to a vector

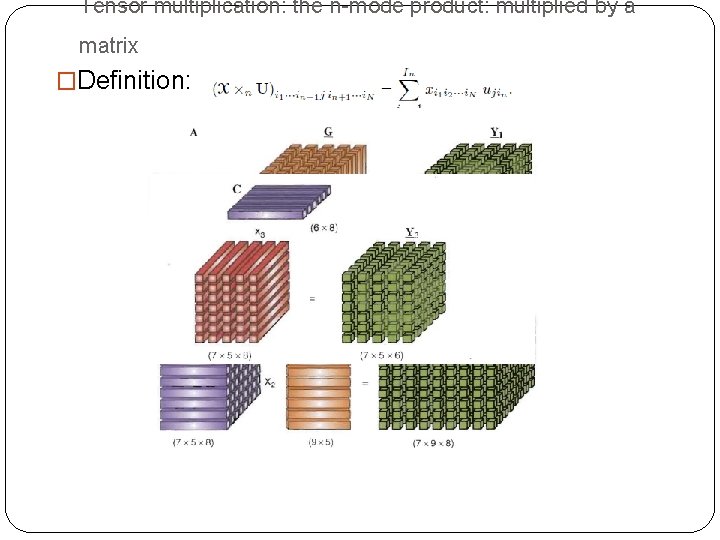
Tensor multiplication: the n-mode product: multiplied by a matrix �Definition:

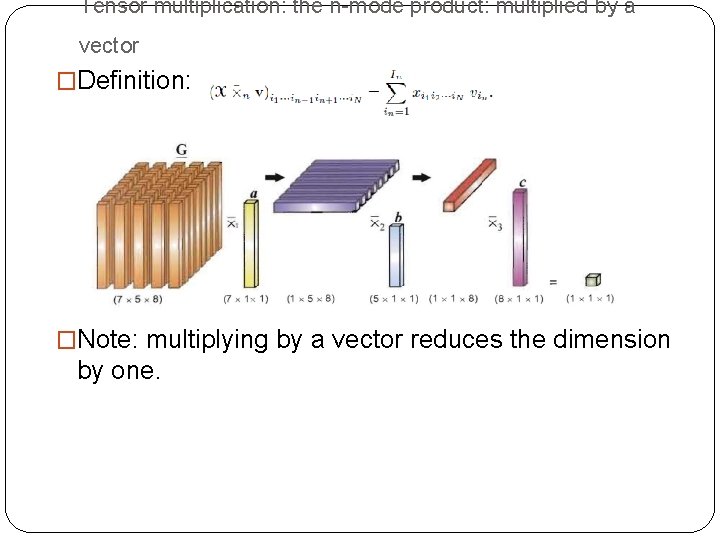
Tensor multiplication: the n-mode product: multiplied by a vector �Definition: �Note: multiplying by a vector reduces the dimension by one.

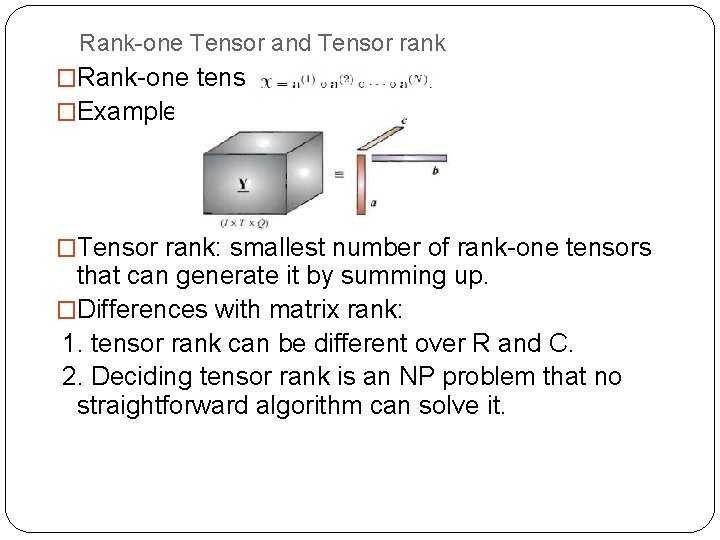
Rank-one Tensor and Tensor rank �Rank-one tensor: �Example: �Tensor rank: smallest number of rank-one tensors that can generate it by summing up. �Differences with matrix rank: 1. tensor rank can be different over R and C. 2. Deciding tensor rank is an NP problem that no straightforward algorithm can solve it.

Tensor factorization: CANDECOMP/PARAFAC factorization(CP) �Tensor factorization: an extension of SVD and PCA of matrix. �CP factorization: �Uniqueness: CP of tensor(higher-order) is unique under some general conditions. �How to compute: Alternative Least Squares(ALS), fixing all but one factor matrix to which LS is applied.

Differences between matrix SVD and tensor CP �Lower-rank approximation is different between matrix and higher-order tensor �Matrix: �Not true for higher-order tensor

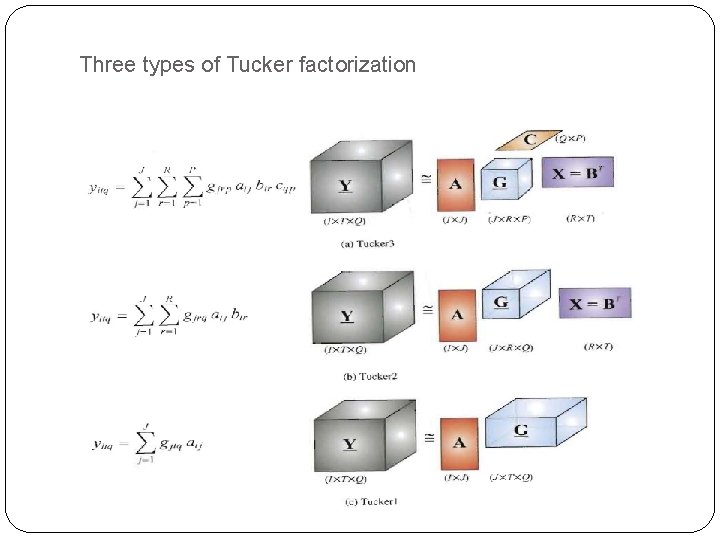
Tensor factorization: Tucker factorization �Tucker factorization: �For three-way tensor, Tucker factorization has three types: 1. Tucker 3: 2. Tucker 2: 3. Tucker 1:

Three types of Tucker factorization

Tucker factorization �Uniqueness: Unlike CP, Tucker factorization is not unique. �How to compute: Higher-order SVD(HOSVD), for each n, Rn:

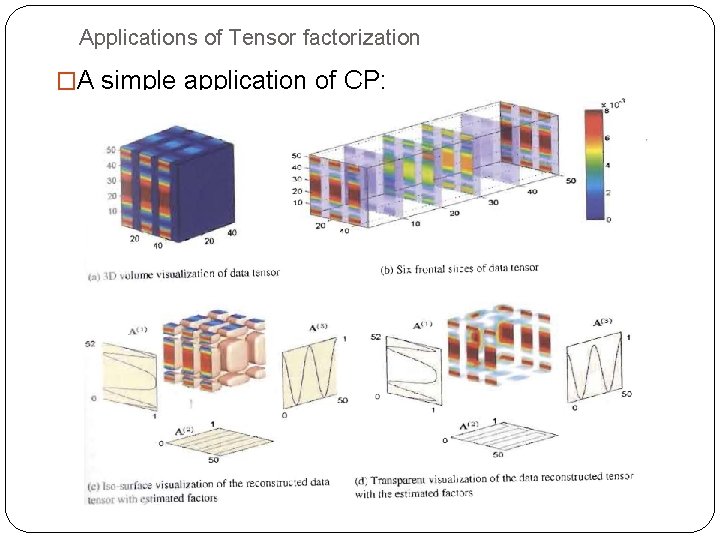
Applications of Tensor factorization �A simple application of CP:

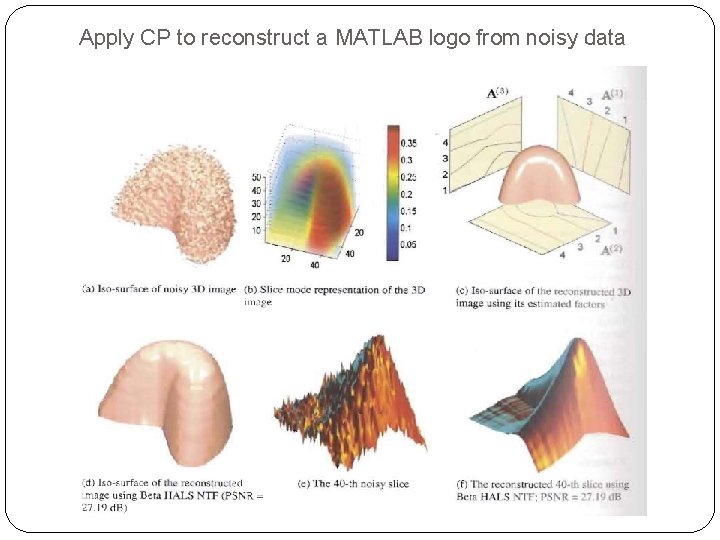
Apply CP to reconstruct a MATLAB logo from noisy data

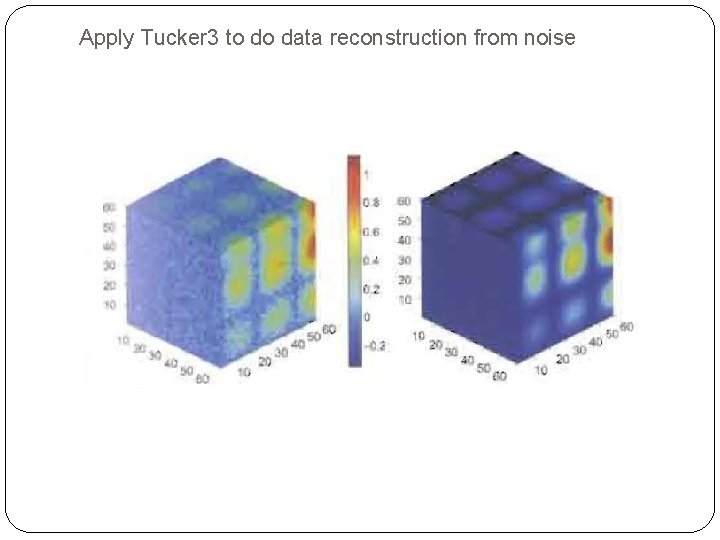
Apply Tucker 3 to do data reconstruction from noise

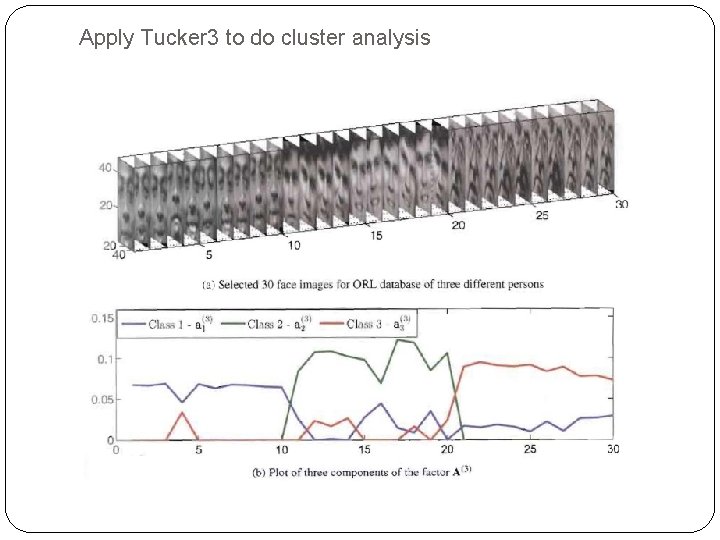
Apply Tucker 3 to do cluster analysis

Conclusion �Tensor is a multidimensional array which is an extension of matrix that arises frequently in our daily life such as video, microarray data, EEG data, etc. �Tensor factorization can be considered higher-order generalization of matrix SVD or PCA, but they also have much differences, such as NP essential of deciding higher-order tensor rank, non-optimal property of higher-order tensor factorization. �There are still many other tensor factorizations, such as block-oriented decomposition, DEDICOM, CANDELINC. �Tensor factorizations have wide applications in data reconstruction, cluster analysis, compression etc.

References �Kolda, Bader, Tensor decompositions and applications. �Martin, an overview of multilinear algebra and tensor decompositions. �Cichocki, etc. , nonnegative matrix and tensor factorizations.