Introduction to Tensor Network States Sukhwinder Singh Macquarie




















- Slides: 58

Introduction to Tensor Network States Sukhwinder Singh Macquarie University (Sydney)

Contents • The quantum many body problem. • Diagrammatic Notation • What is a tensor network? • Example 1 : MPS • Example 2 : MERA

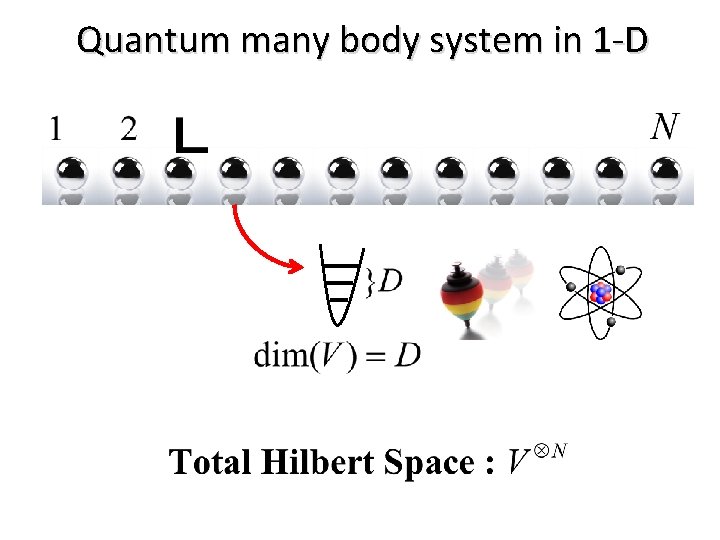
Quantum many body system in 1 -D


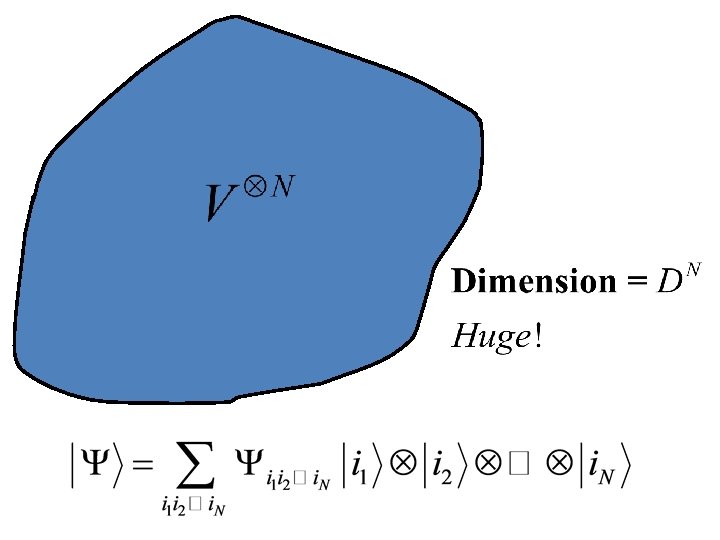
How many qubits can we represent with 1 GB of memory? Here, D = 2. To add one more qubit double the memory.

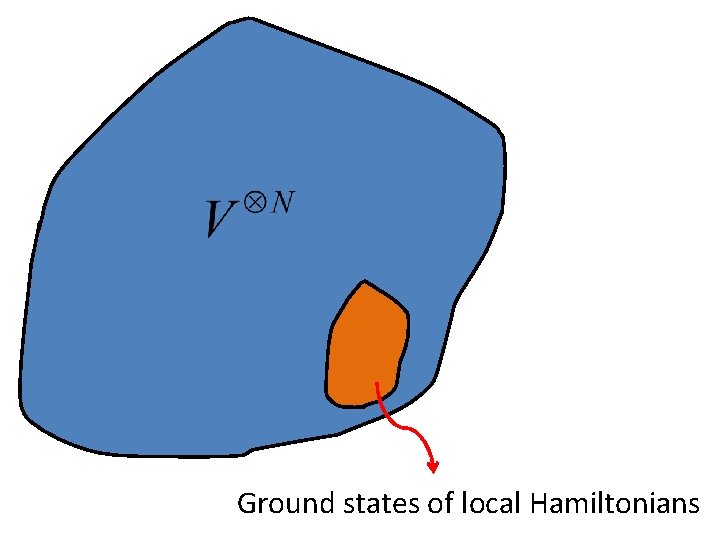
But usually, we are not interested in arbitrary states in the Hilbert space. Typical problem : To find the ground state of a local Hamiltonian H,

Ground states of local Hamiltonians are special

Properties of ground states in 1 -D 1) Gapped Hamiltonian 2) Critical Hamiltonian

We can exploit these properties to represent ground states more efficiently using tensor networks.

Ground states of local Hamiltonians

Contents • The quantum many body problem. • Diagrammatic Notation • What is a tensor network? • Example 1 : MPS • Example 2 : MERA

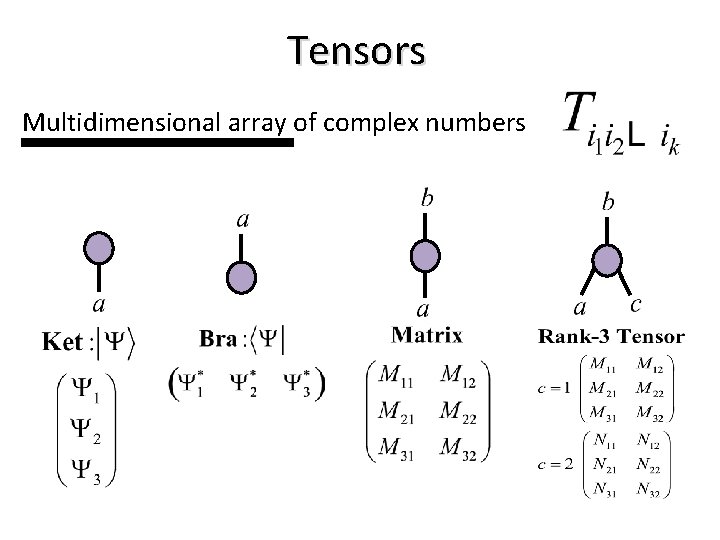
Tensors Multidimensional array of complex numbers

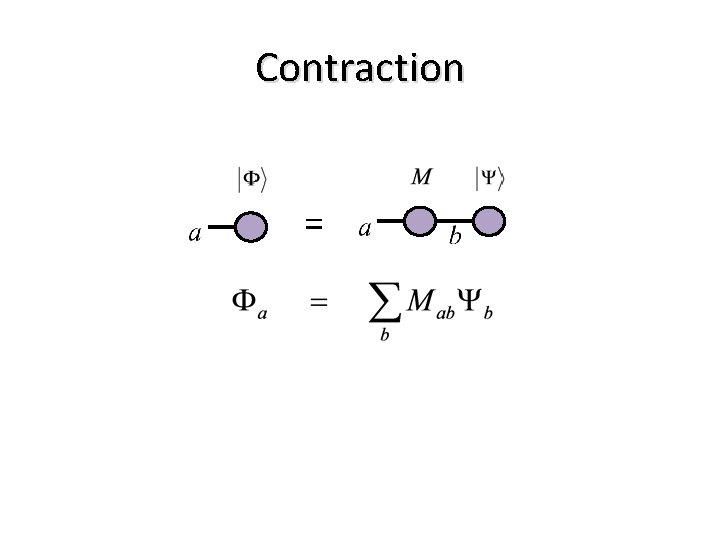
Contraction =

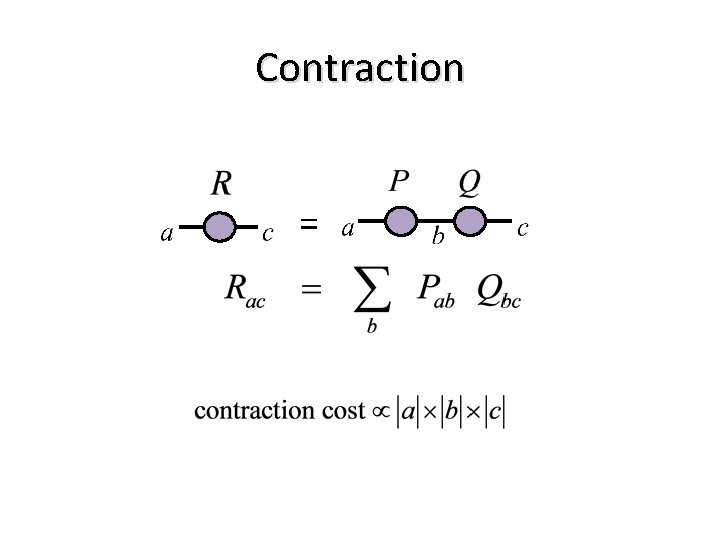
Contraction =

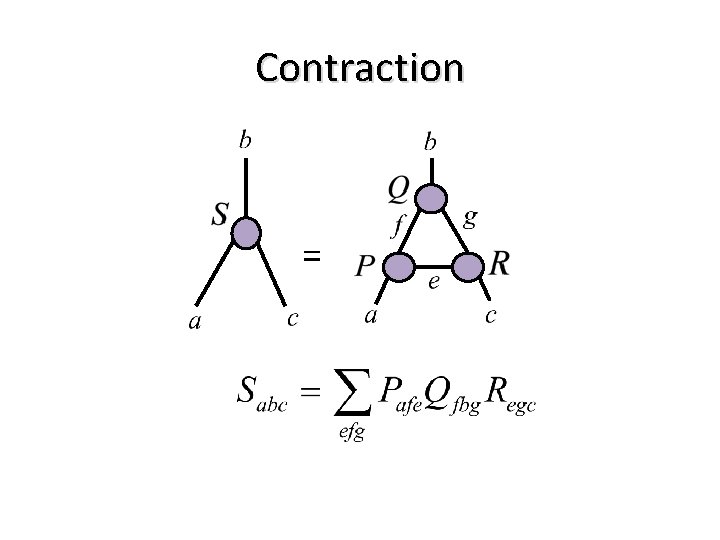
Contraction =

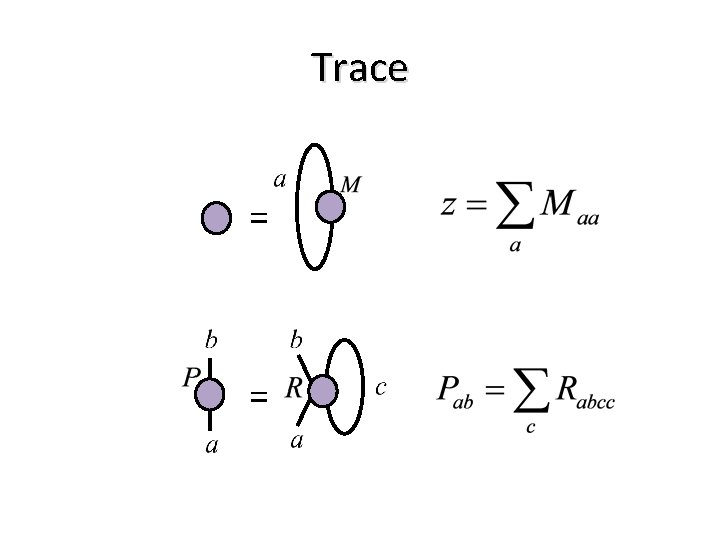
Trace = =

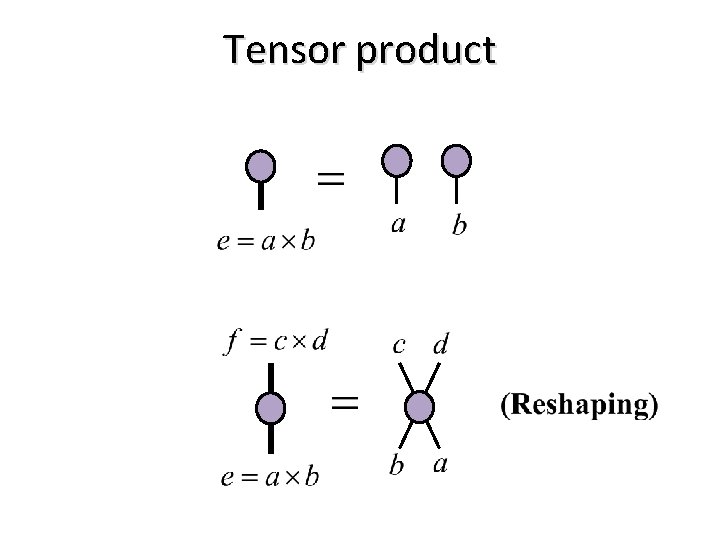
Tensor product

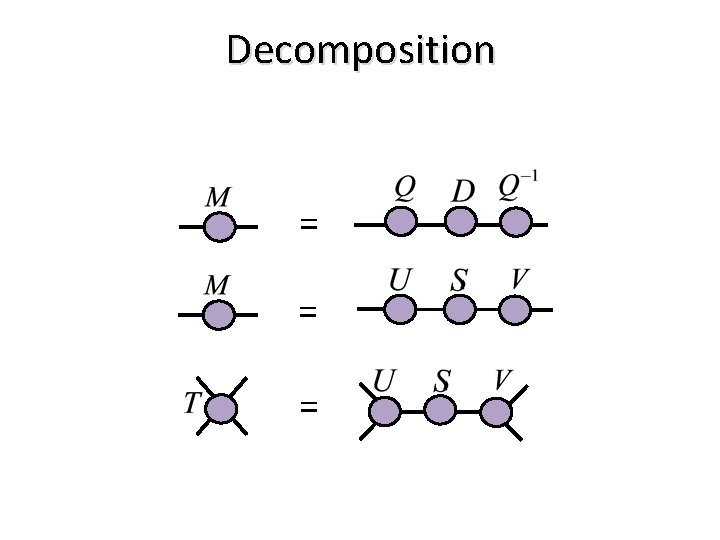
Decomposition = = =

Decomposing tensors can be useful = Rank(M) = Number of components in M = Number of components in P and Q =

Contents • The quantum many body problem. • Diagrammatic Notation • What is a tensor network? • Example 1 : MPS • Example 2 : MERA

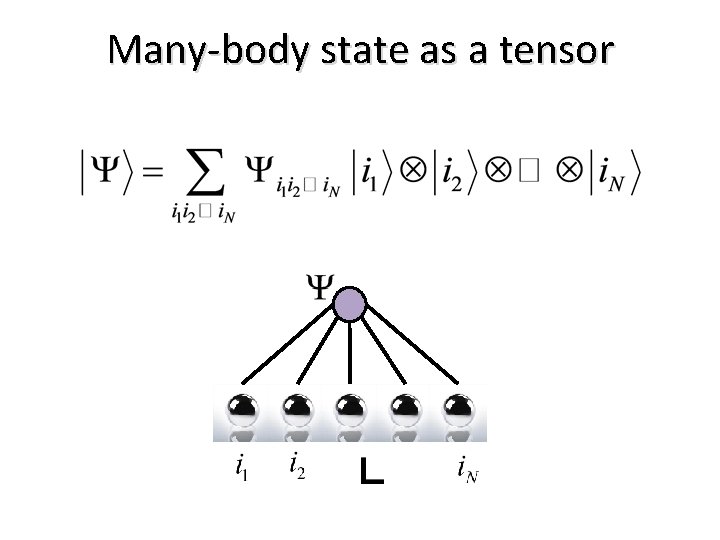
Many-body state as a tensor

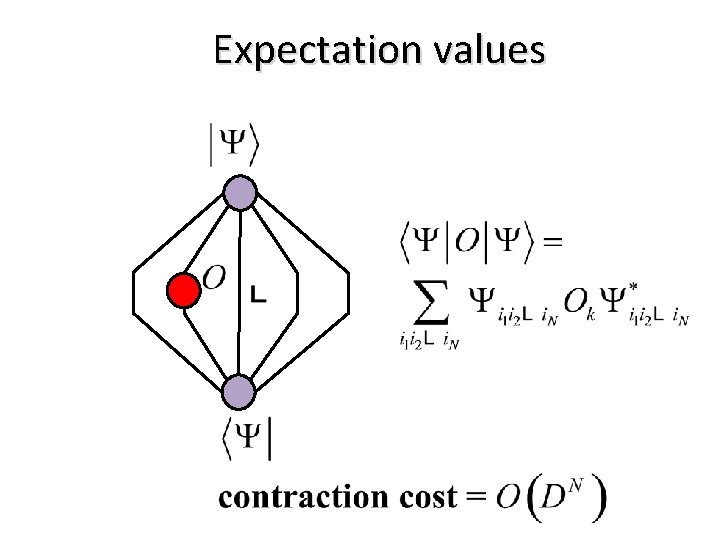
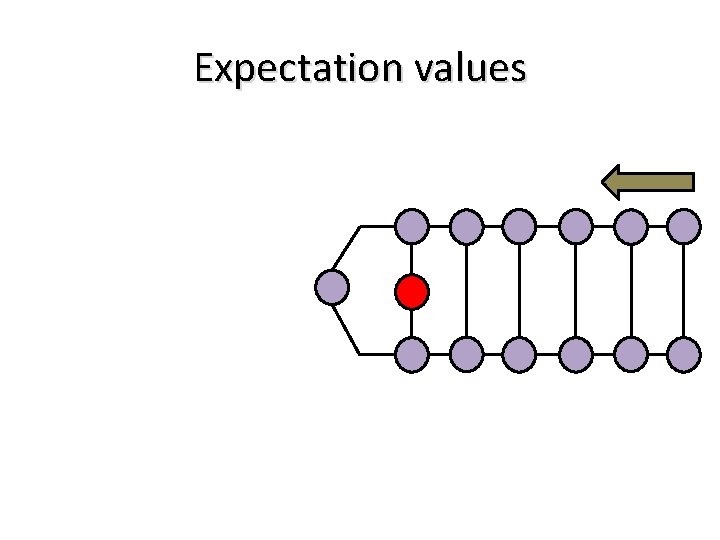
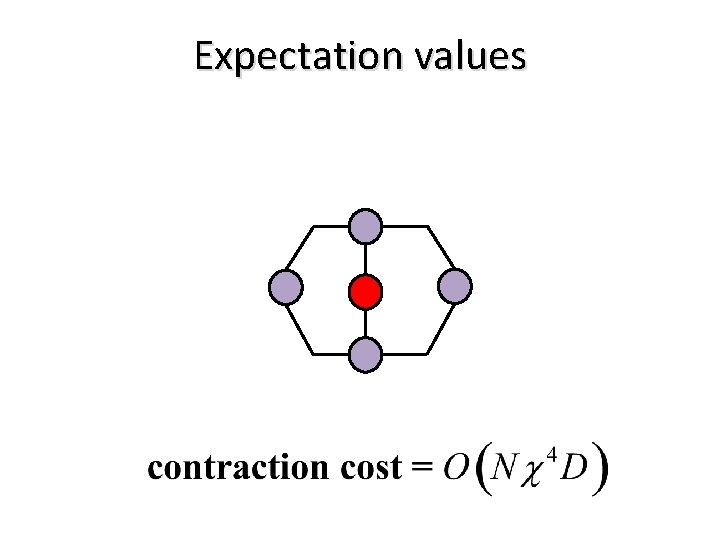
Expectation values

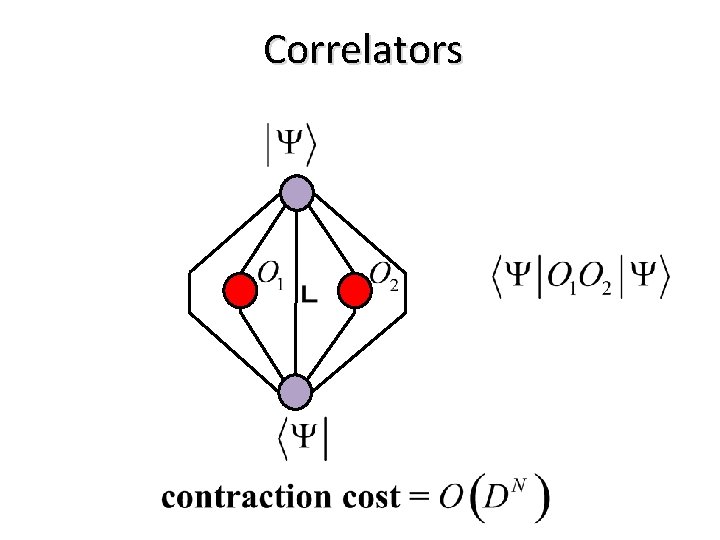
Correlators

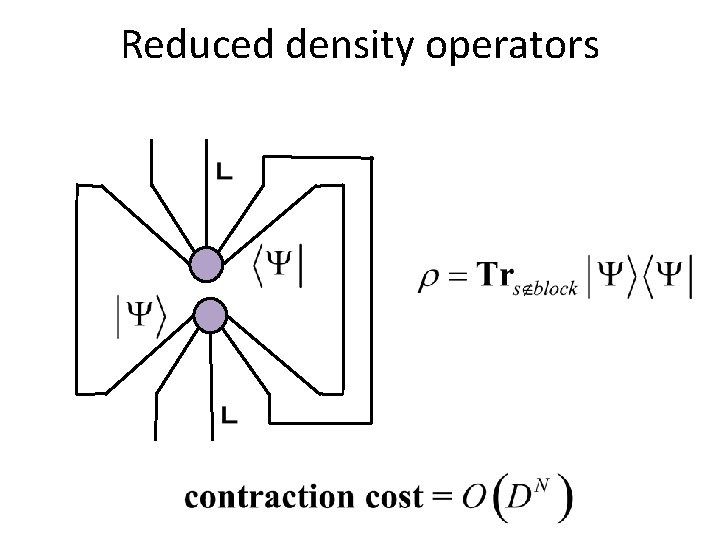
Reduced density operators

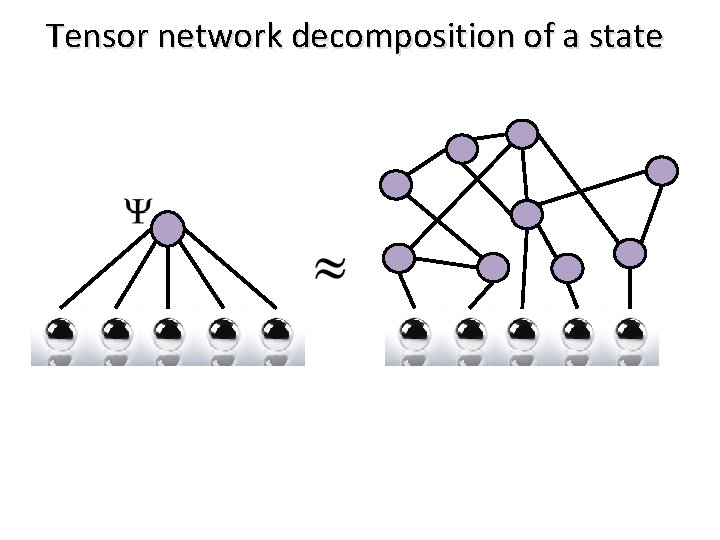
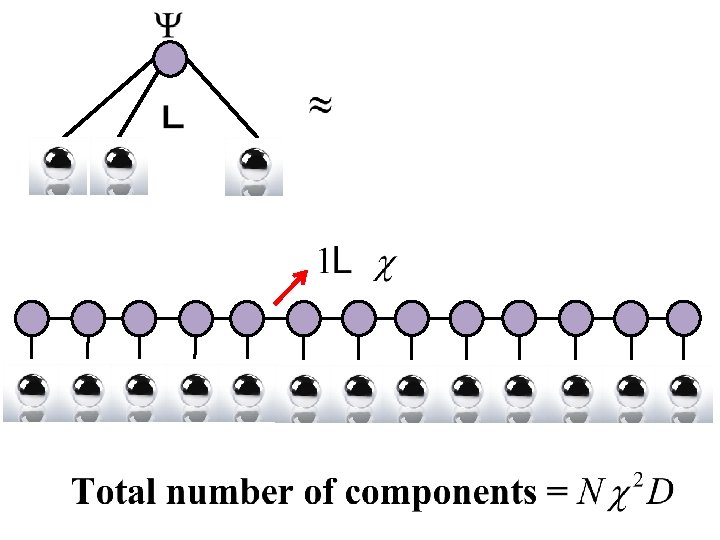
Tensor network decomposition of a state

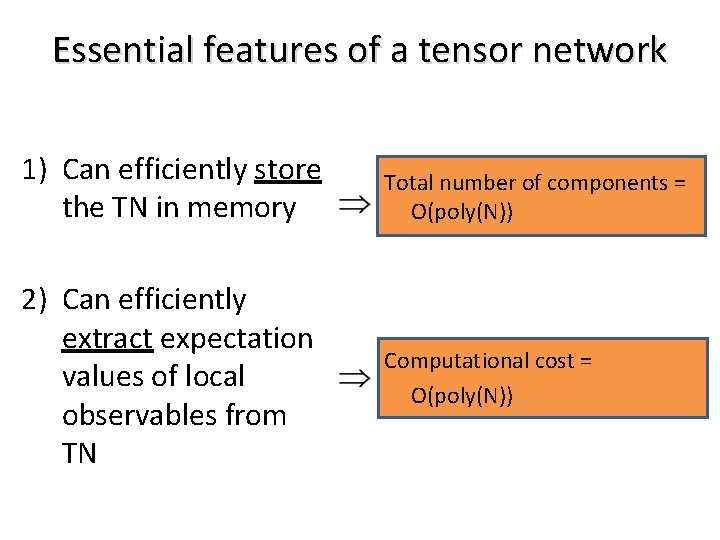
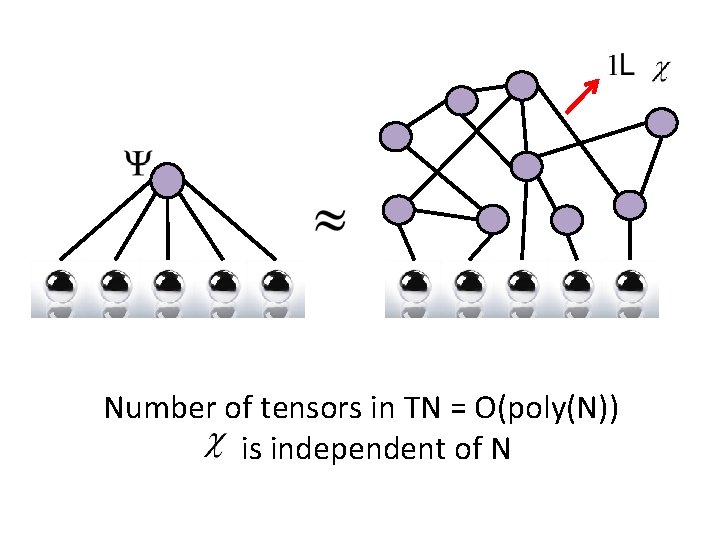
Essential features of a tensor network 1) Can efficiently store the TN in memory Total number of components = O(poly(N)) 2) Can efficiently extract expectation values of local observables from TN Computational cost = O(poly(N))

Number of tensors in TN = O(poly(N)) is independent of N

Contents • The quantum many body problem. • Diagrammatic Notation • What is a tensor network? • Example 1 : MPS • Example 2 : MERA

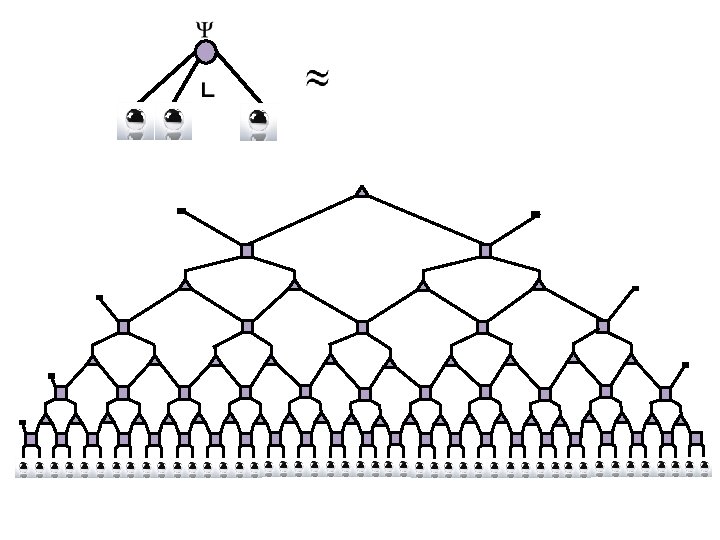
Matrix Product States


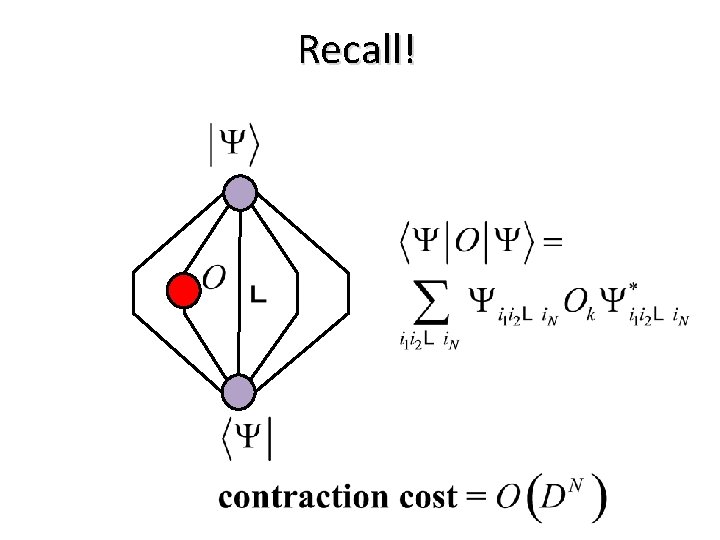
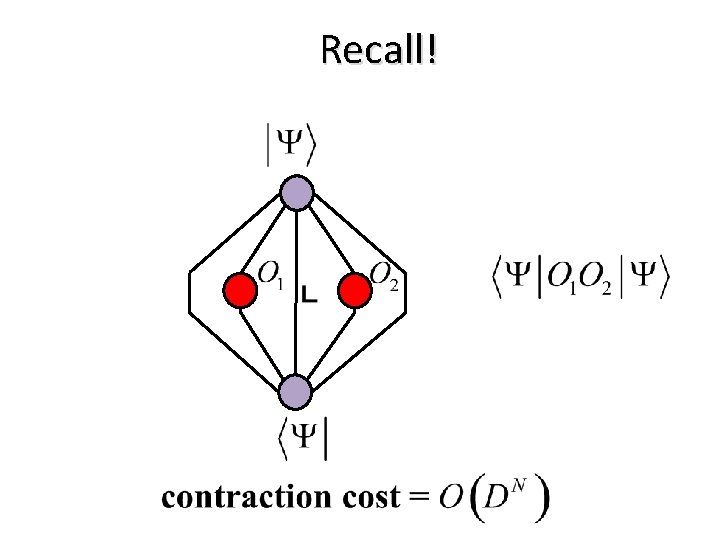
Recall!

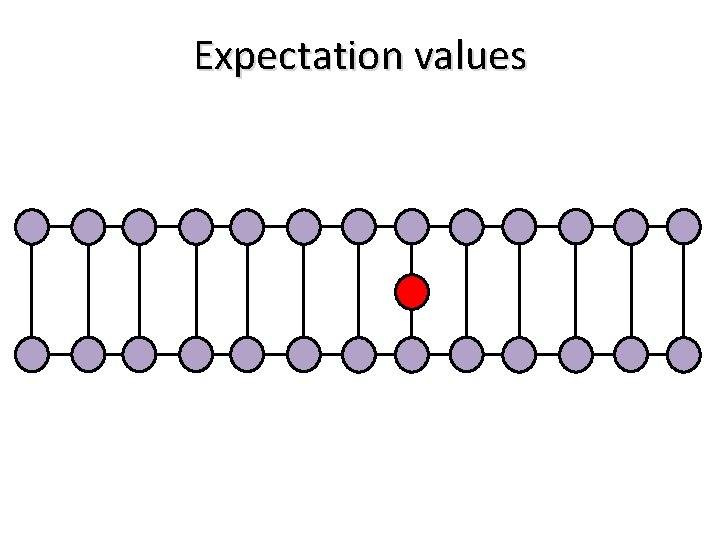
Expectation values

Expectation values

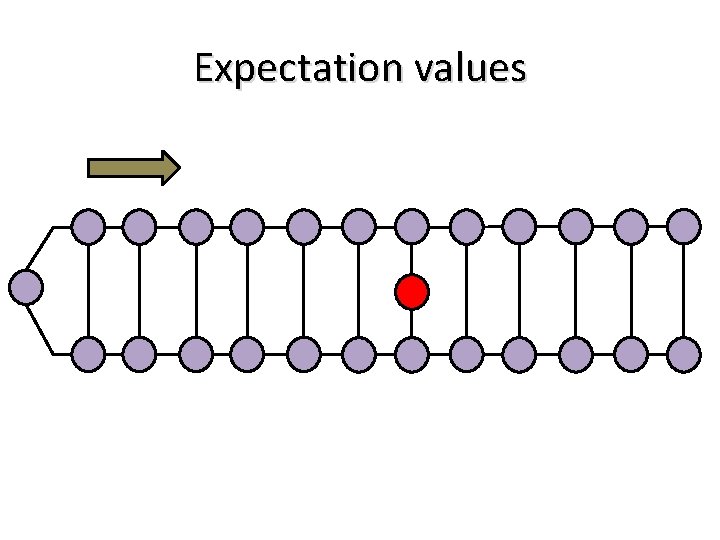
Expectation values

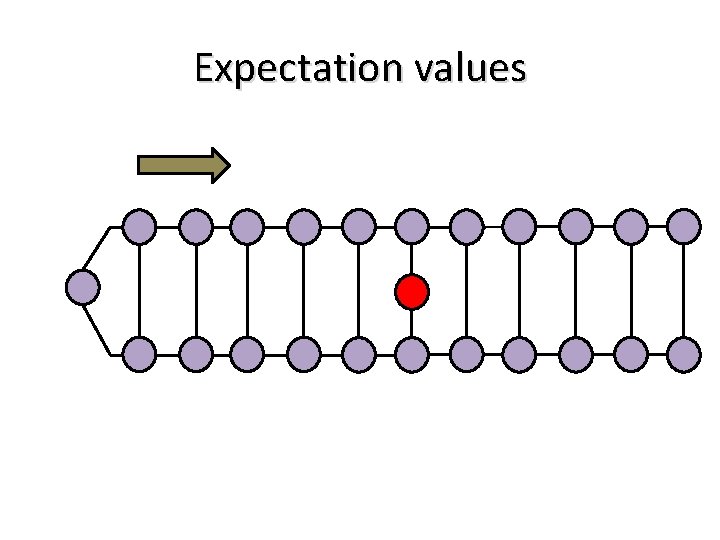
Expectation values

Expectation values

But is the MPS good for representing ground states?

But is the MPS good for representing ground states? Claim: Yes! Naturally suited for gapped systems.

Recall! 1) Gapped Hamiltonian 2) Critical Hamiltonian

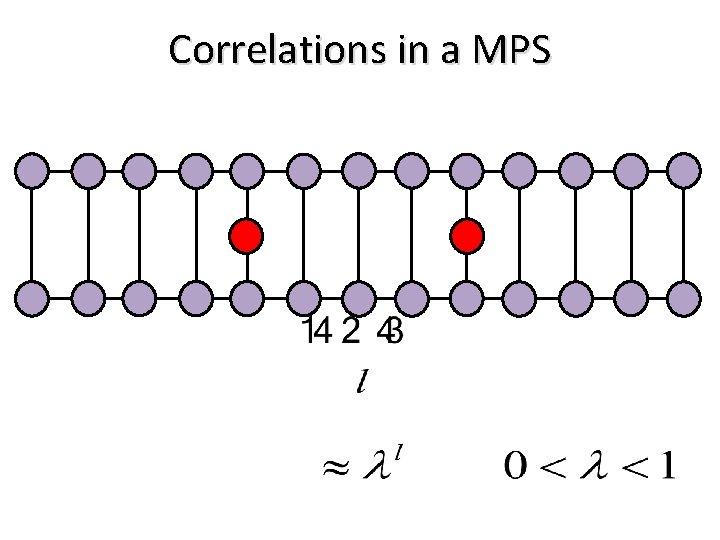
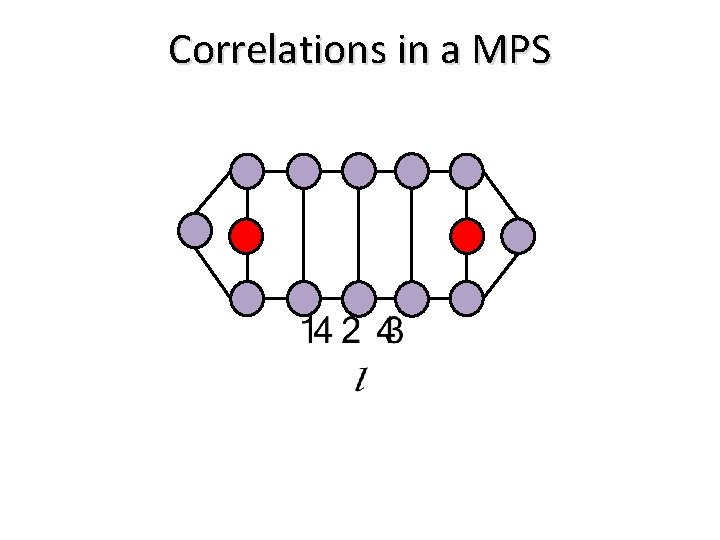
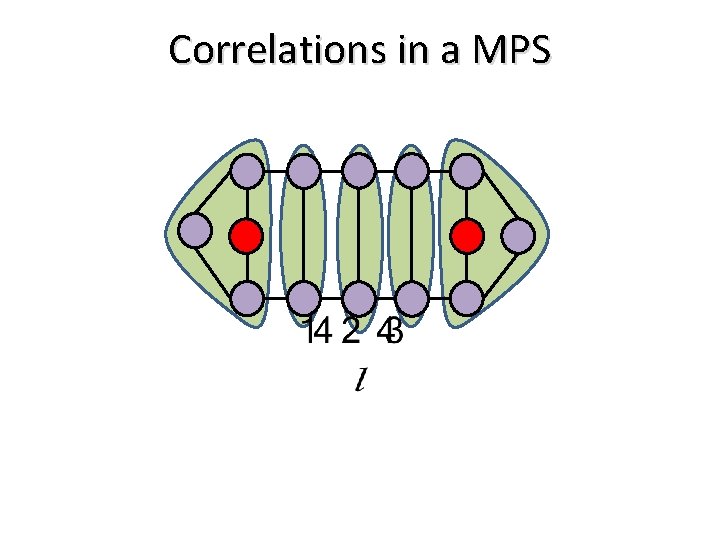
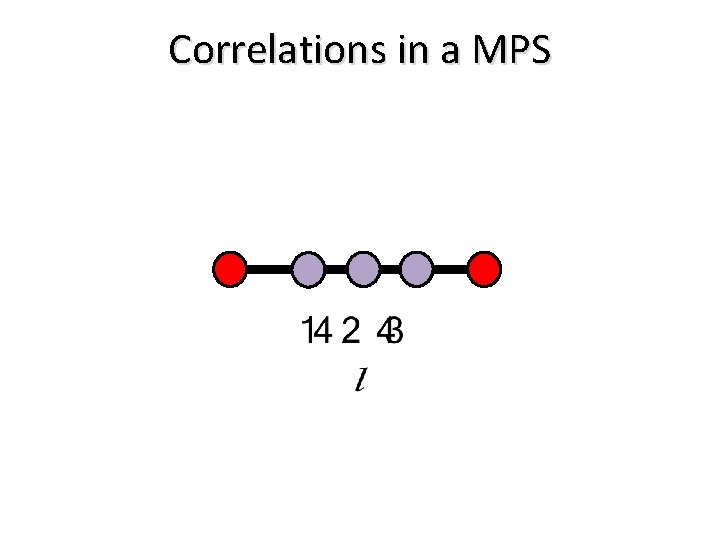
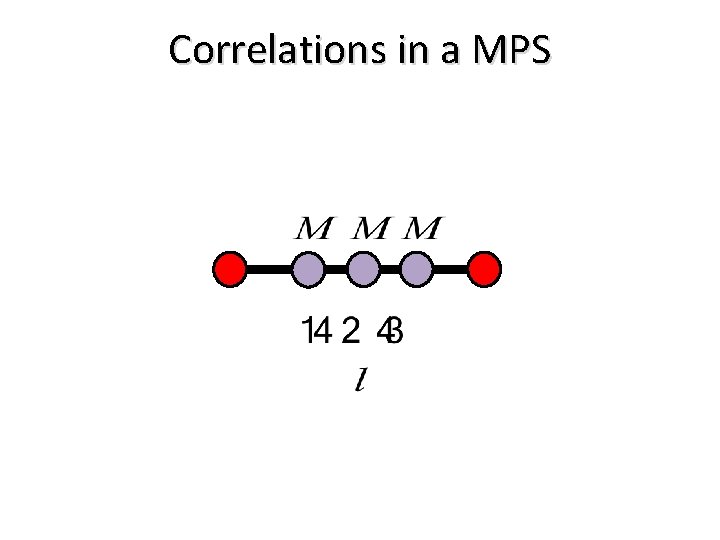
In any MPS Correlations decay exponentially Entropy saturates to a constant

Recall!

Correlations in a MPS

Correlations in a MPS

Correlations in a MPS

Correlations in a MPS

Correlations in a MPS

Correlations in a MPS

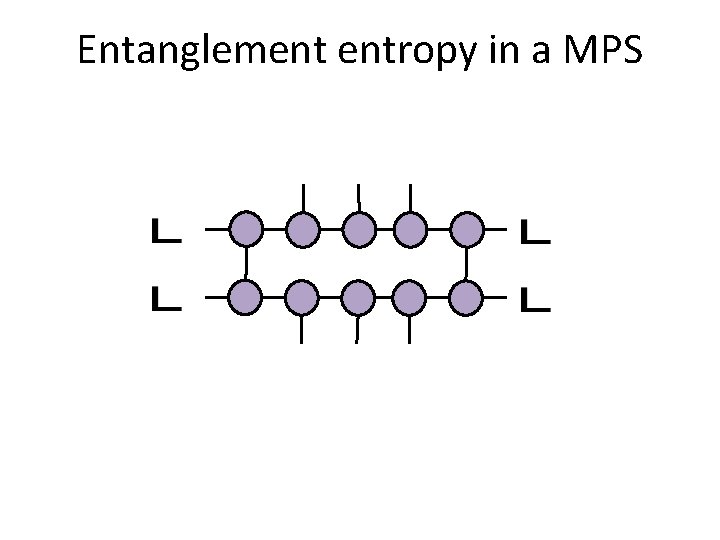
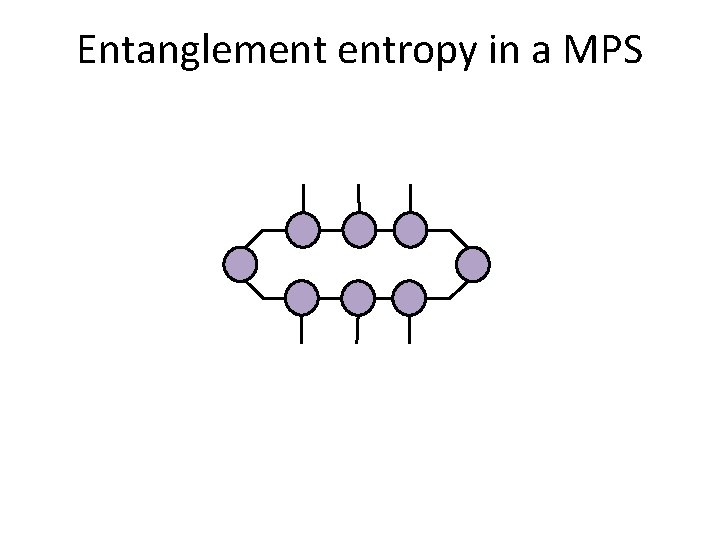
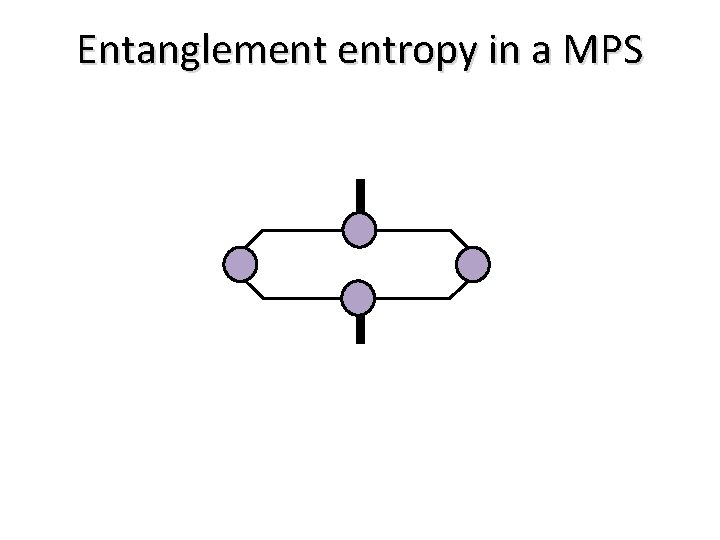
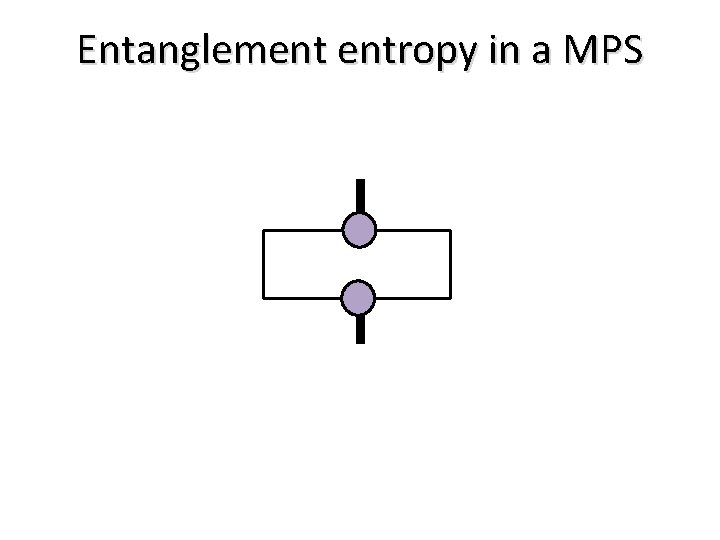
Entanglement entropy in a MPS

Entanglement entropy in a MPS

Entanglement entropy in a MPS

Entanglement entropy in a MPS

Entanglement entropy in a MPS

Entanglement entropy in a MPS

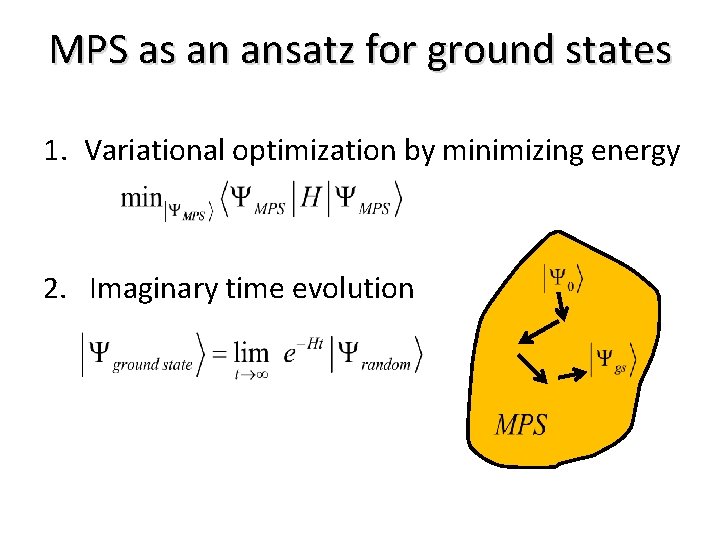
MPS as an ansatz for ground states 1. Variational optimization by minimizing energy 2. Imaginary time evolution

Contents • The quantum many body problem. • Diagrammatic Notation • What is a tensor network? • Example 1 : MPS • Example 2 : MERA


Summary • The quantum many body problem. • Diagrammatic Notation • What is a tensor network? • Example 1 : MPS • Example 2 : MERA

Thanks !