Introduction to Stochastic Models GSLM 54100 1 Outline

Introduction to Stochastic Models GSLM 54100 1

Outline è memoryless property ègeometric and exponential è V(X) = E[V(X|Y)] + V[E(X|Y)] è conditional probability 2

Memoryless Property of Geometric Distribution è X ~ Geo (p) è Y = the remaining life of given that X > 1 è Y = (X-1|X > 1) è P(Y = k) = P(X - 1 = k| X > 1) = = = (1 -p)k-1 p = P(X = k) è Y ~ X è similarly, (X - m|X > m) ~ X for all m 1 è the memoryless property of Geometric 3

Memoryless Property of Exponent Distribution è X ~ exp( ), P(X > s) = e s, s > 0 è Y = the remaining life of given that X > t (> 0) è Y = (X-t|X > t) è P(Y > s) = P(X - t > s| X > t) = = = e s = P(X > s) è Y ~ X è the memoryless property of exponential 4

Finding Variance by Conditioning 5

Finding Variance By Conditioning Proposition 3. 1 of Ross è X & Y: two random variables è both V(X|Y) and E(X|Y) being random variables è well-defined E[V(X|Y)] & V[E(X|Y)] è E[V(X|Y)] = E[E(X 2|Y)] - E[E 2(X|Y)] è V[E(X|Y)] = E[E 2(X|Y)] - E 2[E(X|Y)] è E[V(X|Y)] + V[E(X|Y)] = E[E(X 2|Y)] E 2[E(X|Y)] = E[X 2] E 2[X] = V(X) 6

Variance of Random Sum è Xi's ~ i. i. d. random variables, mean & variance 2 è N: an integer non-negative random variable independent of Xi's, mean & variance 2 è S = 7

Variance of Random Sum è V(S) = E[V(S|N)] + V[E(S|N)] è V(S|N = n) = V( ) = n 2 èE[V(S|N)] = E[N 2] = 2 E[N] = 2 è E(S|N = n) = E( ) = n èV[E(S|N)] = V[N ] = 2 V(N) = 2 2 è V(S) = 2 + 2 2 ènot necessary to find the distribution of S 8

Variance of Geometric è X ~ Geo(p), 0 < p < 1 è IA = 1 if {X = 1} and IA = 0 if {X > 1} èP(IA = 1) = p and P(IA = 0) = 1 -p = q è E[V(X|IA)] èV(X|X=1) = 0 èV(X|X>1) = V(1+X-1|X>1) = V(X) è E[V(X|IA)] = p 0 + q. V(X) = q. V(X) 9

Variance of Geometric Example 3. 18 of Ross è V[E(X|IA)] èE[X|X=1] = 1 memoryless property of geometric èE[X|X>1] = 1+ E[X-1| X>1] = èV[E(X|IA)] = E[E 2(X|IA)] - E 2[E(X| IA)] è 10

Conditional Probability 11

First Part of Example 3. 26 of Ross è n men mixed their hats & randomly picked one è En: no matches for these n men è P(En) = ? è p 1 = 0 è p 2 = 0. 5 12

First Part of Example 3. 26 of Ross è n = 3 A a è M: correct hat for the first man B b è Mc: wrong hat for the first man C c è p 3 = P(E 3) = P(E 3|M)P(M) + P(E 3|Mc)P(Mc) = P(E 3|Mc)P(Mc) è P(Mc) = 2/3 & P(E 3|Mc) = 1/2 13

First Part of Example 3. 26 of Ross è n = 4 A a è M: correct hat for the first man B b è Mc: wrong hat for the first man C c D d è p 4 = P(E 4) = P(E 4|M)P(M) + P(E 4|Mc)P(Mc) = P(E 4|Mc)P(Mc) è P(Mc) = 3/4 & P(E 4|Mc) = ? ? ? 14

First Part of Example 3. 26 of Ross è P(E 4|Mc) = ? ? ? A a è Ca: C gets a B b è Cna: C does not get a C c D d è {E 4|Mc} = {E 4 Ca|Mc} {E 4 Cna|Mc} è P(E 4|Mc) = P(E 4 Ca|Mc) + P(E 4 Cna|Mc) 15

First Part of Example 3. 26 of Ross è P(E 4 Cna|Mc) = P(E 3) A a è P(E 4 Ca|Mc) B b C c D d = P(E 4|Ca Mc)P(Ca|Mc) = P(E 2)(2/3) 16

First Part of Example 3. 26 of Ross è è è è pn = P(En) = P(En|M)P(M) + P(En|Mc)P(Mc) = P(En|Mc)P(Mc) Ha: the man whose hat picked by A picked A’s hat Hna: the man whose hat picked by A did not pick A’s hat P(En|Mc) = P(En Hna|Mc) + P(En Ha|Mc) P(En Hna|Mc) = pn-1 P(En Ha|Mc) = P(En|Ha Mc)P(Ha|Mc) = pn-2(1/n-1) so solving 17

Recursive Relationships 18

Ex. #4 of WS#10 è #1. (Solve Exercise #4 of Worksheet #10 by conditioning, not direct computation. ) Let X and Y be two independent random variables ~ geo(p). è (a). Find P(X = Y). è (b). Find P(X > Y). è (c). Find P(min(X, Y) > k) for k {1, 2, …}. è (d). From (c) or otherwise, Find E[min(X, Y)]. è (e). Show that max(X, Y) + min(X, Y) = X + Y. Hence find E[max(X, Y)]. 19

Ex. #4 of WS#10 è (a). different ways to solve the problem è by computation: è P(X = Y) = = p/(2 -p) 20

Ex. #4 of WS#10 è by conditioning: è P(X = Y|X = 1, Y = 1) = 1 è P(X = Y|X = 1, Y > 1) = 0 è P(X = Y|X > 1, Y = 1) = 0 è P(X = Y|X > 1, Y > 1) = P(X = Y) è P(X = Y) = P(X = 1, Y = 1)(1) + P(X > 1, Y > 1)P(X = Y) è P(X = Y) = p 2 + (1 p)2 P(X = Y) i. e. , P(X = Y) = p/(2 p) 21

Ex. #4 of WS#10 è (b) P(X > Y) è by symmetry è P(X > Y) + P(X = Y) + P(X < Y) = 1 è P(X > Y) = P(X < Y) è P(X > Y) = = 22

Ex. #4 of WS#10 è by direct computation è P(X > Y) = 23

Ex. #4 of WS#10 è by conditioning è P(X > Y) = E[P(X > Y|Y)] è P(X > Y|Y = y) = P(X > y) = (1 -p)y è E[P(X > Y|Y)] = E[(1 -p)Y] 24

Ex. #4 of WS#10 è yet another way of conditioning è P(X > Y|X = 1, Y = 1) = 0 è P(X > Y|X = 1, Y > 1) = 0 è P(X > Y|X > 1, Y = 1) = 1 è P(X > Y|X > 1, Y > 1) = P(X > Y) = P(X > 1, Y = 1) + P(X > 1, Y > 1)P(X > Y) = (1 -p)p + (1 -p)2 P(X > Y) è P(X > Y) = (1 p)/(2 p) è 25

Ex. #5 of WS#10 è In the sea battle of Cape of No Return, two cruisers of country Landpower (unluckily) ran into two battleships of country Seapower. With artilleries of shorter range, the two cruisers had no choice other than receiving rounds of bombardment by the two battleships. Suppose that in each round of bombardment, a battleship only aimed at one cruiser, and it sank the cruiser with probability p in a round, 0 < p < 1, independent of everything else. The two battleships fired simultaneously in each round. 26

Ex. #5 of WS#10 (a) Suppose that the two battleships first co-operated together to sink the same cruiser. Find the expected number of rounds of bombardment taken to sink both of the two cruisers. è pc = P(a cruiser was sunk in a round) = 1 - P(a cruiser was not sunk in a round) = 1 -(1 -p)2 è expected number of rounds taken to sink a cruiser ~ Geo(pc) with mean = 1/pc è expected number of rounds taken to sink two cruisers = 2/pc è 27

Ex. #5 of WS#10 è (b) Now suppose that initially the two battleships aimed at a different cruiser. They helped the other battleship only if its targeted cruiser was sunk before the other one. è (i) What is the probability that the two cruisers were sunk at the same time (with the same number of rounds of bombardment). 28

Ex. #5 of WS#10 è (b). (i). Ni = the number of rounds taken to sink the ith cruiser; Ni ~ Geo (p); N 1 and N 2 are independent. è ps = P(2 cruisers sunk at the same round) = P(N 1 = N 2) èdiscussed before 29

Ex. #5 of WS#10 è different ways to solve the problem è by computation: è P(N 1 = N 2) = = = = p/(2 -p) 30

Ex. #5 of WS#10 è by conditioning: è P(N 1 = N 2|N 1 = 1, N 2 = 1) = 1 è P(N 1 = N 2|N 1 = 1, N 2 > 1) = 0 è P(N 1 = N 2|N 1 > 1, N 2 = 1) = 0 è P(N 1 = N 2|N 1 > 1, N 2 > 1) = P(X = Y) è P(N 1 = N 2) = P(N 1 = 1, N 2 = 1)(1) + P(N 1 = 1, N 2 = 1)P(X = Y) è P(N 1 = N 2) = p 2 + (1 p)2 P(N 1 = N 2) i. e. , P(N 1 = N 2) = p/(2 p) 31

Ex. #5 of WS#10 è (ii). Find the probability of taking k ( {1, 2, …}) rounds to have the first sinking of a cruiser. è Y = the number of rounds to have the first sinking of a cruiser è different ways to find P(Y = k) 32

Ex. #5 of WS#10 è from the tail distribution è P(min(N 1, N 2) > k) = P(N 1 > k, N 2 > k) = P(N 1 > k)P(N 2 > k) = (1 -p)2 k è P(Y = k) = P(Y > k-1) - P(Y > k) = P(min(N 1, N 2) > k -1) - P(min(N 1, N 2) > k) = P(N 1 > k – 1, N 2 > k – 1) - P(N 1 > k, N 2 > k) = P(N 1 > k – 1)P(N 2> k – 1) - P(N 1> k)P(N 2> k) = (1 p)2 k-2 (1 p)2 k = (1 p)2 k-2 p(2 p) 33

Ex. #5 of WS#10 è from direct calculation è P(Y = k) = P(min(N 1, N 2) = k) = P(N 1 = k, N 2 = k) + P(N 1 > k, N 2 = k) + P(N 1 = k, N 2 > k) = P(N 1 = k)P(N 2 = k) + P(N 1 > k)P(N 2 = k) + P(N 1 = k) P(N 2 > k) = (1 p)2 k-2 p 2 + 2(1 p)k-1 p = (1 p)2 k-2 p(2 p) 34

Ex. #5 of WS#10 è (iii). Find the expected number of rounds taken to have the first sinking of a cruiser è different ways to find E(Y) è by direct computation èE(Y) = = 35

Ex. #5 of WS#10 è from the tail distribution èE(Y) = = = = 36

Ex. #5 of WS#10 è by conditioning è E[min(N 1, N 2)|N 1 = 1, N 2 = 1] = 1 è E[min(N 1, N 2)|N 1 = 1, N 2 > 1] = 1 è E[min(N 1, N 2)|N 1 > 1, N 2 = 1] = 1 è E[min(N 1, N 2)|N 1 > 1, N 2 > 1] = 1 + E[min(N 1, N 2)] è E[min(N 1, N 2)] = 1 + (1 -p)2 E[min(N 1, N 2)] è E[min(N 1, N 2)] = 37

Ex. #5 of WS#10 è (iv). Z = # of rounds taken to sink both cruisers; find E(Z) è by conditioning èE(Z|N 1 = 1, N 2 = 1) = 1 èE(Z|N 1 = 1, N 2 > 1) = 1 + E(N 2’) èE(Z|N 1 > 1, N 2 = 1) = 1 + E(N 1’) èE(Z|N 1 > 1, N 2 > 1) = 1 + E(Z) 38

Ex. #5 of WS#10 è N 1’, N 2’ ~ Geo( 1 (1 p)2) è E(Z) = è solving E(Z) = 39

Ex. #5 of WS#10 è by direct computation Solving, 40

Exercise 3. 62 of Ross è A, B, and C are evenly matched tennis players. Initially A and B play a set, and the winner then plays C. This continues, with the winner always playing the waiting player, until one of the players has won two sets in a row. That player is then declared the overall winner. Find the probability that A is the overall winner. 41

Exercise 3. 62 of Ross è by direct computation è convention of a sample point: x 1 x 2…xn , where xj is the winner of the jth match èAA = A first beats B and then beats C è sample points with A winning the first match and eventually winning the game èAA ACBACBAA … è sample points with A losing the first match but eventually winning the game èBCAA BCACBACBAA … 42

Exercise 3. 62 of Ross è by direct computation èP(A wins the game) = P(AA ACBACBAA …) + P(BCAA BCACBACBAA …) = = èP(B wins the game) = èP(C wins the game) = 43

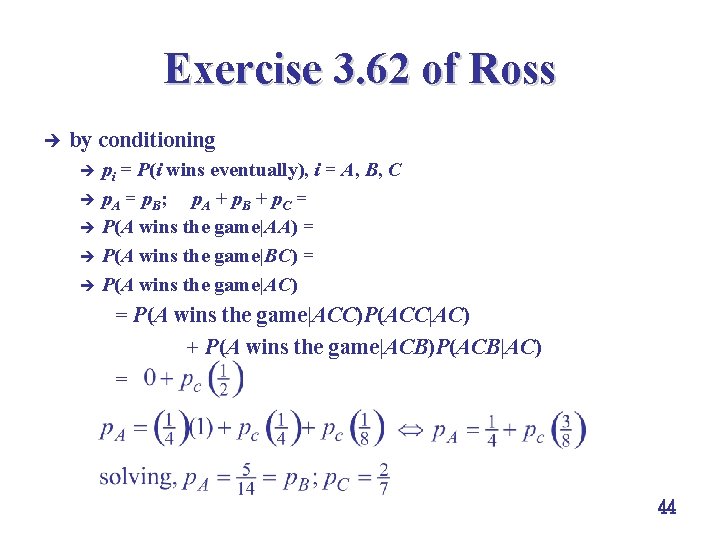
Exercise 3. 62 of Ross è by conditioning pi = P(i wins eventually), i = A, B, C è p. A = p. B; p. A + p. B + p. C = 1 è P(A wins the game|AA) = 1; P(A wins the game|BB) = 0 è P(A wins the game|BC) = p. C è P(A wins the game|AC) è = P(A wins the game|ACC)P(ACC|AC) + P(A wins the game|ACB)P(ACB|AC) = 44

Stochastic Modeling è given a problem statement è formulate the problem by defining events, random variables, etc. è understand the stochastic mechanism è deduce means (including probabilities, variances, etc. ) èidentifying special structure and In the sea battle of Cape of No Return, two cruisers of country Landpower (unluckily) ran into two battleships of country Seapower. With artilleries of shorter range, the two cruisers had no choice other than receiving rounds of bombardment by the two battleships. Suppose that in each round of bombardment, a battleship only aimed at one cruiser, and it sank the cruiser with probability p in a round, 0 < p < 1, independent of everything else. The two battleships fired simultaneously in each round. (b) Now suppose that initially the two battleships aimed at a different cruiser. They helped the other battleship only if its targeted cruiser was sunk before the other one. (i) What is the probability that the two cruisers were sunk at the same time (with the same number of rounds of bombardment). properties of the stochastic mechanism 45

Examples of Ross in Chapter 3 è Examples 3. 2, 3. 3, 3. 4, 3. 5, 3. 6, 3. 7, 3. 11, 2. 12, 3. 13 46

Exercises of Ross in Chapter 3 è Exercises 3. 1, 3. 3, 3. 5, 3. 7, 3. 8, 3. 14, 3. 21, 3. 23, 3. 24, 3. 25, 3. 27, 3. 29, 3. 30, 3. 34, 3. 37, 3. 40, 3. 41, 3. 44, 3. 49, 3. 51, 3. 54, 3. 61, 3. 62, 3. 63, 3. 64, 3. 66 47