Introduction to Statistics with Graph Pad Prism 8

Introduction to Statistics with Graph. Pad Prism 8 Anne Segonds-Pichon v 2019 -03

Outline of the course • Power analysis with G*Power • Basic structure of a Graph. Pad Prism project • Analysis of qualitative data: • Chi-square test • Analysis of quantitative data: • Student’s t-test, One-way ANOVA, correlation and curve fitting

Power analysis • Definition of power: probability that a statistical test will reject a false null hypothesis (H 0). • Translation: the probability of detecting an effect, given that the effect is really there. • In a nutshell: the bigger the experiment (big sample size), the bigger the power (more likely to pick up a difference). • Main output of a power analysis: • Estimation of an appropriate sample size • Too big: waste of resources, • Too small: may miss the effect (p>0. 05)+ waste of resources, • Grants: justification of sample size, • Publications: reviewers ask for power calculation evidence, • Home office: the 3 Rs: Replacement, Reduction and Refinement.

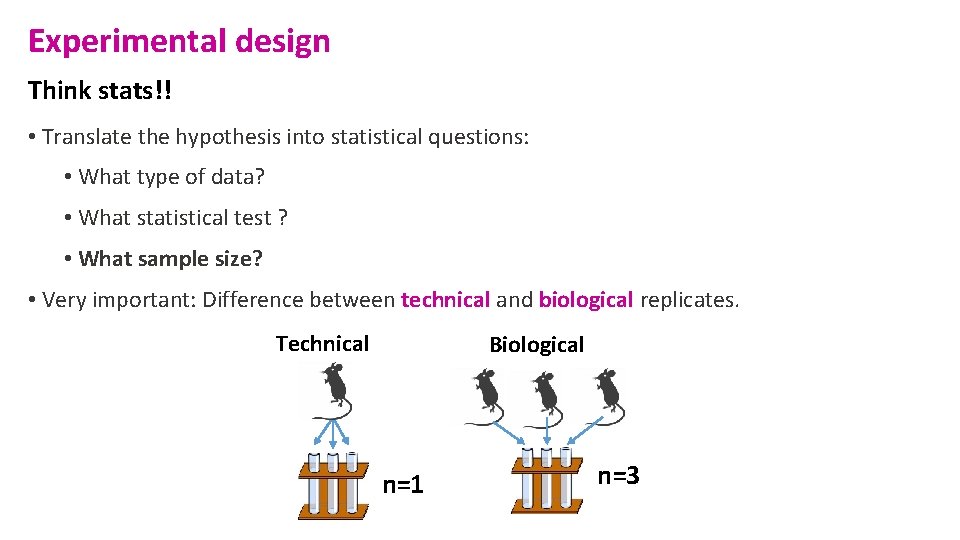
Experimental design Think stats!! • Translate the hypothesis into statistical questions: • What type of data? • What statistical test ? • What sample size? • Very important: Difference between technical and biological replicates. Technical Biological n=1 n=3

Power analysis A power analysis depends on the relationship between 6 variables: • the difference of biological interest • the variability in the data (standard deviation) Effect size • the significance level (5%) • the desired power of the experiment (80%) • the sample size • the alternative hypothesis (ie one or two-sided test)

1 The difference of biological interest • This is to be determined scientifically, not statistically. • minimum meaningful effect of biological relevance • the larger the effect size, the smaller the experiment will need to be to detect it. • How to determine it? • Substantive knowledge, previous research, pilot study … 2 The Standard Deviation (SD) • Variability of the data • How to determine it? • Substantive knowledge, previous research, pilot study … • In ‘power context’: effect size: combination of both: • e. g. : Cohen’s d = (Mean 1 – Mean 2)/Pooled SD

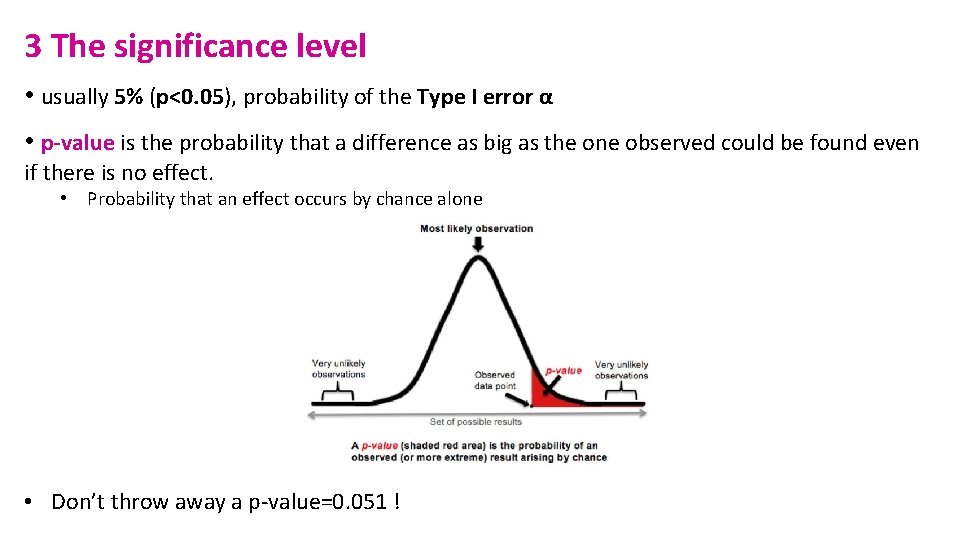
3 The significance level • usually 5% (p<0. 05), probability of the Type I error α • p-value is the probability that a difference as big as the one observed could be found even if there is no effect. • Probability that an effect occurs by chance alone • Don’t throw away a p-value=0. 051 !

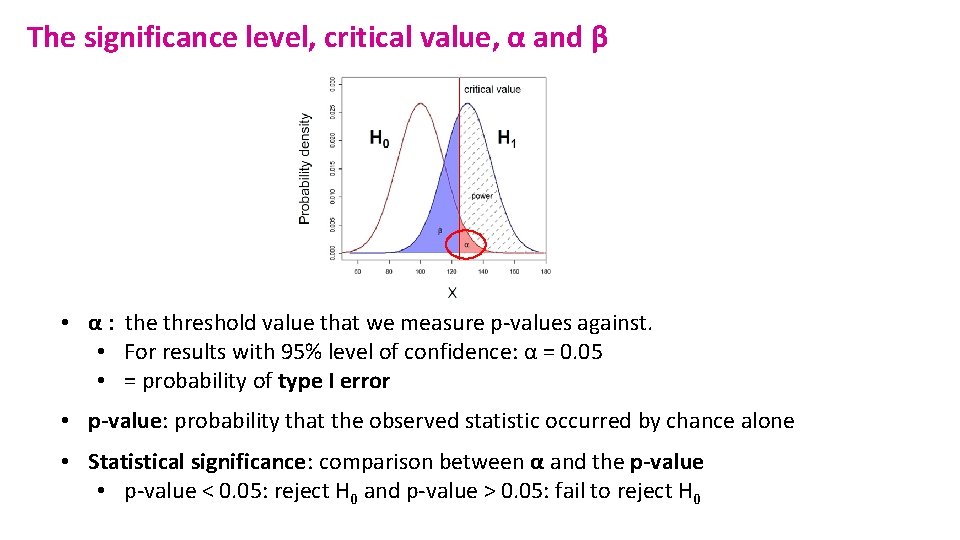
The significance level, critical value, α and β • α : the threshold value that we measure p-values against. • For results with 95% level of confidence: α = 0. 05 • = probability of type I error • p-value: probability that the observed statistic occurred by chance alone • Statistical significance: comparison between α and the p-value • p-value < 0. 05: reject H 0 and p-value > 0. 05: fail to reject H 0

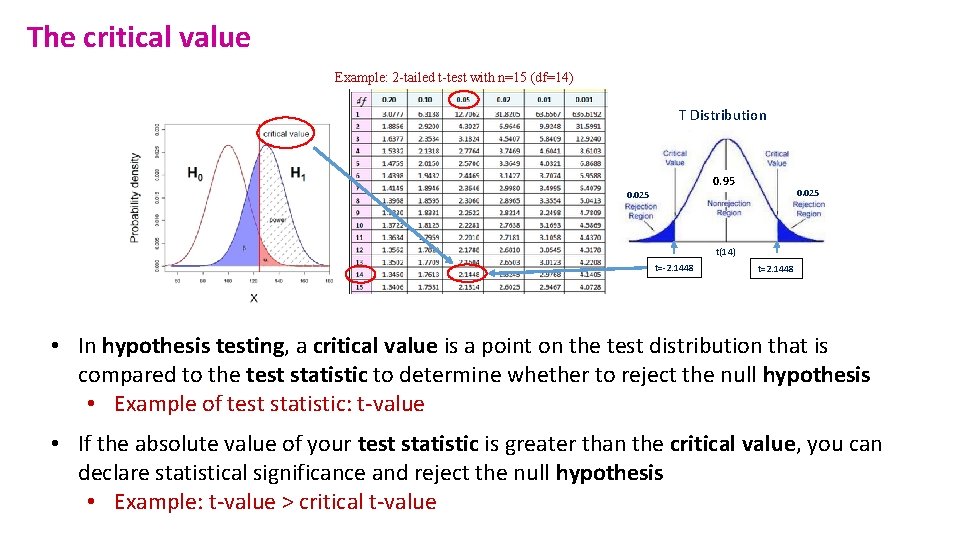
The critical value Example: 2 -tailed t-test with n=15 (df=14) T Distribution 0. 95 0. 025 t(14) t=-2. 1448 t=2. 1448 • In hypothesis testing, a critical value is a point on the test distribution that is compared to the test statistic to determine whether to reject the null hypothesis • Example of test statistic: t-value • If the absolute value of your test statistic is greater than the critical value, you can declare statistical significance and reject the null hypothesis • Example: t-value > critical t-value

4 The desired power: 80% • Type II error (β) is the failure to reject a false H 0 • Direct relationship between Power and type II error: • if β = 0. 2 and Power = 1 – β = 0. 8 (80%) • Hence a true difference will be missed 20% of the time • General convention: 80% but could be more or less • Cohen (1988): • For most researchers: Type I errors are four times more serious than Type II errors: 0. 05 * 4 = 0. 2 • Compromise: 2 groups comparisons: 90% = +30% sample size, 95% = +60%

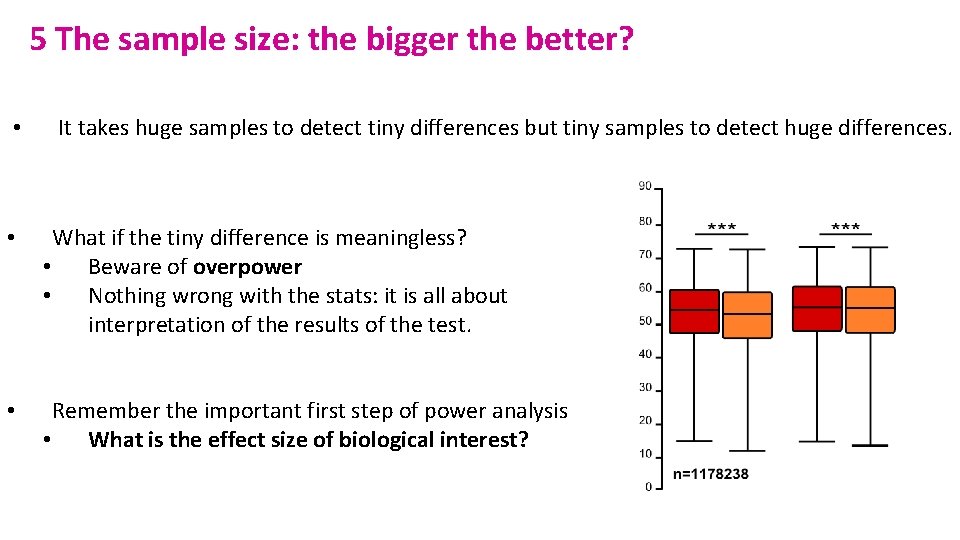
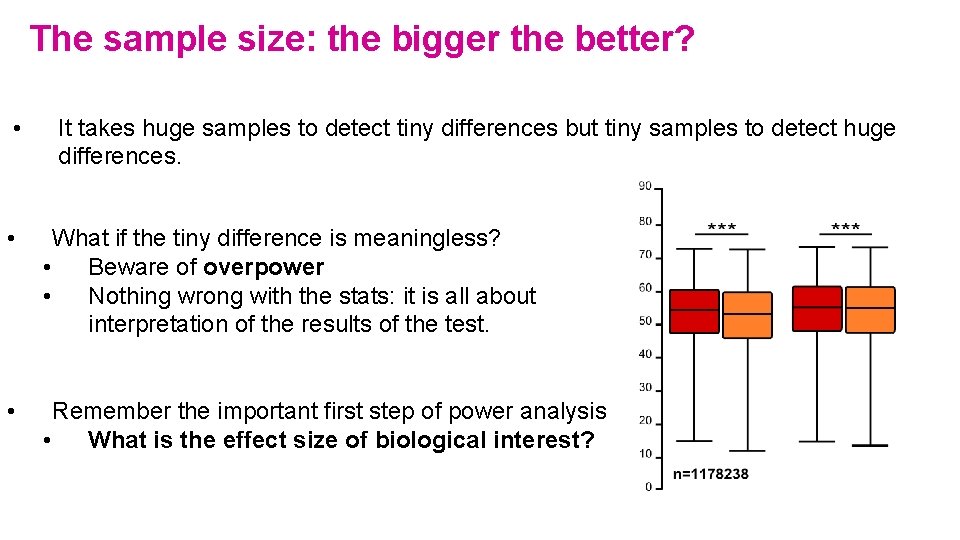
5 The sample size: the bigger the better? • It takes huge samples to detect tiny differences but tiny samples to detect huge differences. • What if the tiny difference is meaningless? • Beware of overpower • Nothing wrong with the stats: it is all about interpretation of the results of the test. • Remember the important first step of power analysis • What is the effect size of biological interest?

6 The alternative hypothesis • One-tailed or 2 -tailed test? One-sided or 2 -sided tests? • Is the question: • • Is there a difference? Is it bigger than or smaller than? Can rarely justify the use of a one-tailed test Two times easier to reach significance with a one-tailed than a two-tailed • Suspicious reviewer!

To recapitulate: • The null hypothesis (H 0): H 0 = no effect • The aim of a statistical test is to reject or not H 0. Statistical decision True state of H 0 True (no effect) H 0 False (effect) Reject H 0 Type I error α False Positive Correct True Positive Do not reject H 0 Correct True Negative Type II error β False Negative • Traditionally, a test or a difference are said to be “significant” if the probability of type I error is: α =< 0. 05 • High specificity = low False Positives = low Type I error • High sensitivity = low False Negatives = low Type II error

Hypothesis Experimental design Choice of a Statistical test Power analysis: Sample size Experiment(s) Data exploration Statistical analysis of the results

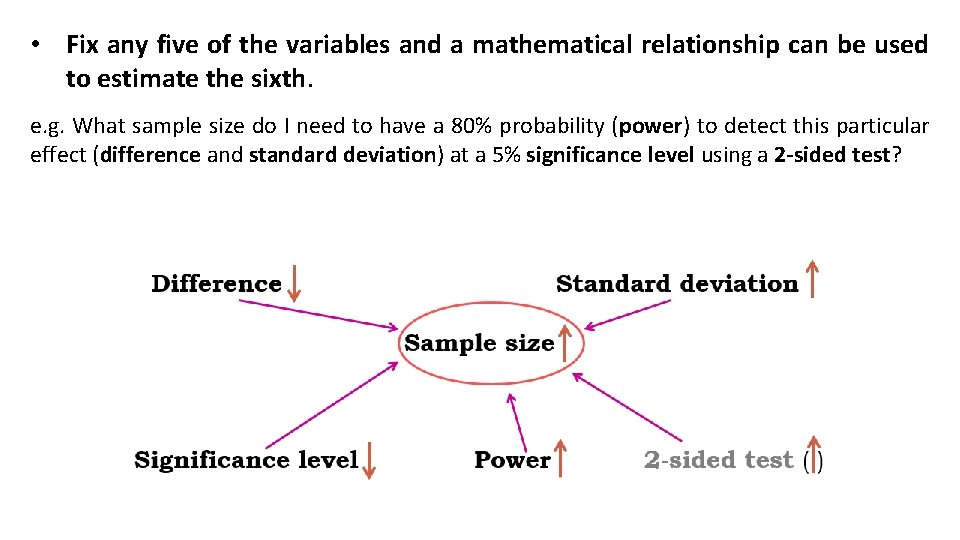
• Fix any five of the variables and a mathematical relationship can be used to estimate the sixth. e. g. What sample size do I need to have a 80% probability (power) to detect this particular effect (difference and standard deviation) at a 5% significance level using a 2 -sided test?

• Good news: there are packages that can do the power analysis for you . . . providing you have some prior knowledge of the key parameters! difference + standard deviation = effect size • Free packages: • R • G*Power and In. Vivo. Stat • Russ Lenth's power and sample-size page: • http: //www. divms. uiowa. edu/~rlenth/Power/ • Cheap package: Stat. Mate (~ $95) • Not so cheap package: Med. Calc (~ $495)

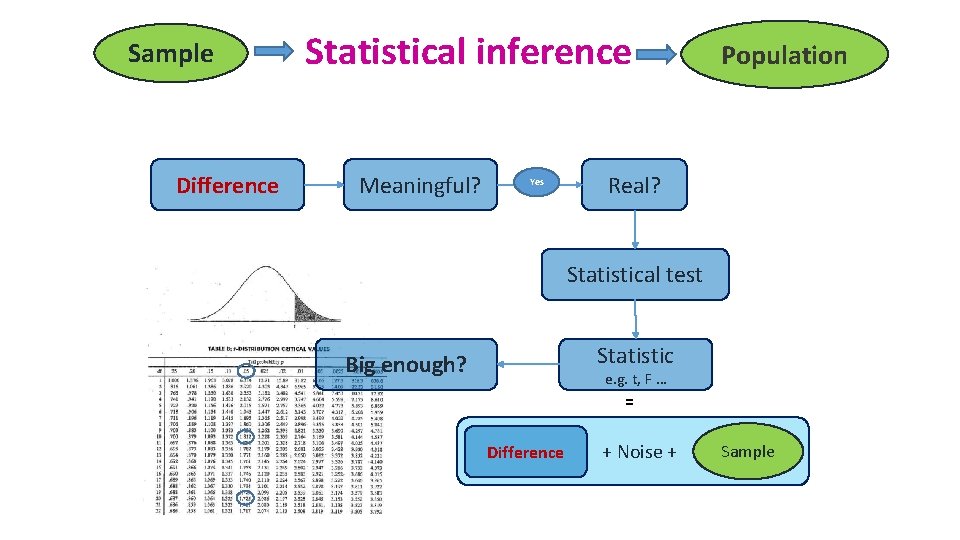
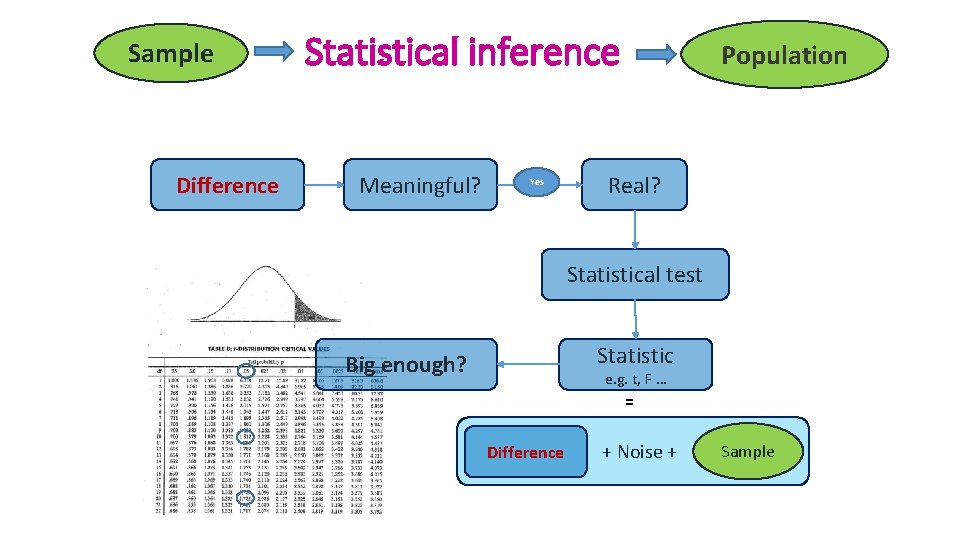
Sample Difference Statistical inference Meaningful? Yes Population Real? Statistical test Statistic Big enough? e. g. t, F … = Difference + Noise + Sample

Qualitative data

Qualitative data • = not numerical • = values taken = usually names (also nominal) • e. g. causes of death in hospital • Values can be numbers but not numerical • e. g. group number = numerical label but not unit of measurement • Qualitative variable with intrinsic order in their categories = ordinal • Particular case: qualitative variable with 2 categories: binary or dichotomous • e. g. alive/dead or presence/absence

Fisher’s exact and Chi 2 Example: cats and dogs. xlsx • Cats and dogs trained to line dance • 2 different rewards: food or affection • Question: Is there a difference between the rewards? • Is there a significant relationship between the 2 variables? – does the reward significantly affect the likelihood of dancing? • To answer this type of question: – Contingency table – Fisher’s exact or Chi 2 tests But first: how many cats do we need? Food Affection Dance ? ? No dance ? ?

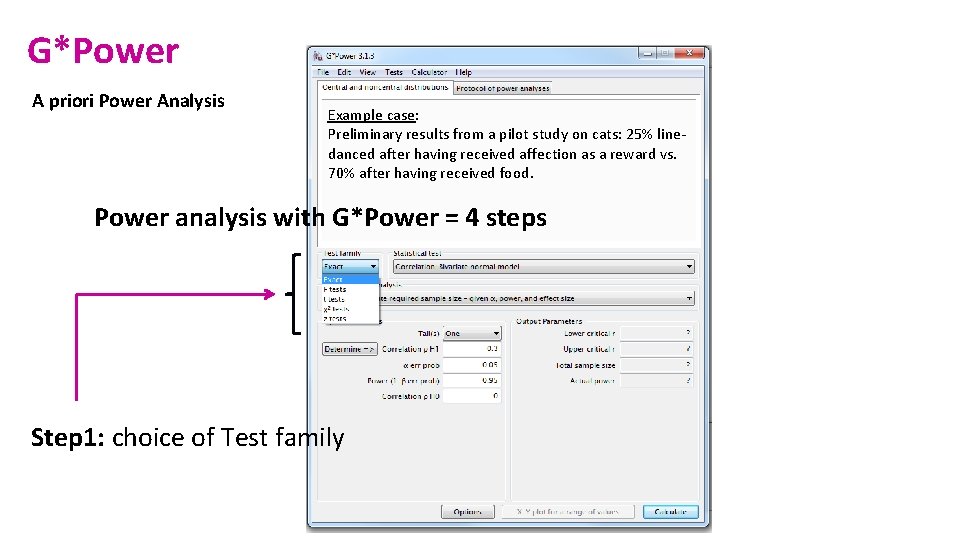
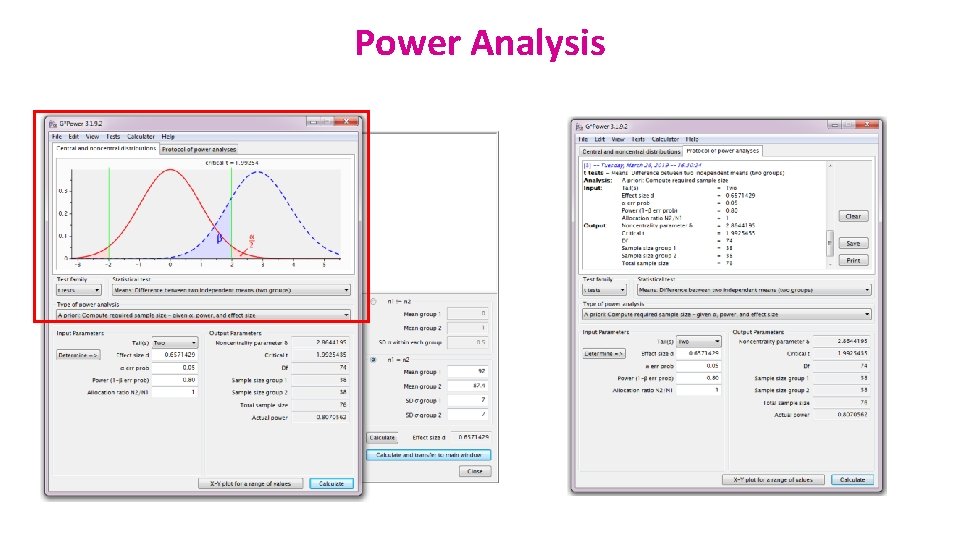
G*Power A priori Power Analysis Example case: Preliminary results from a pilot study on cats: 25% linedanced after having received affection as a reward vs. 70% after having received food. Power analysis with G*Power = 4 steps Step 1: choice of Test family

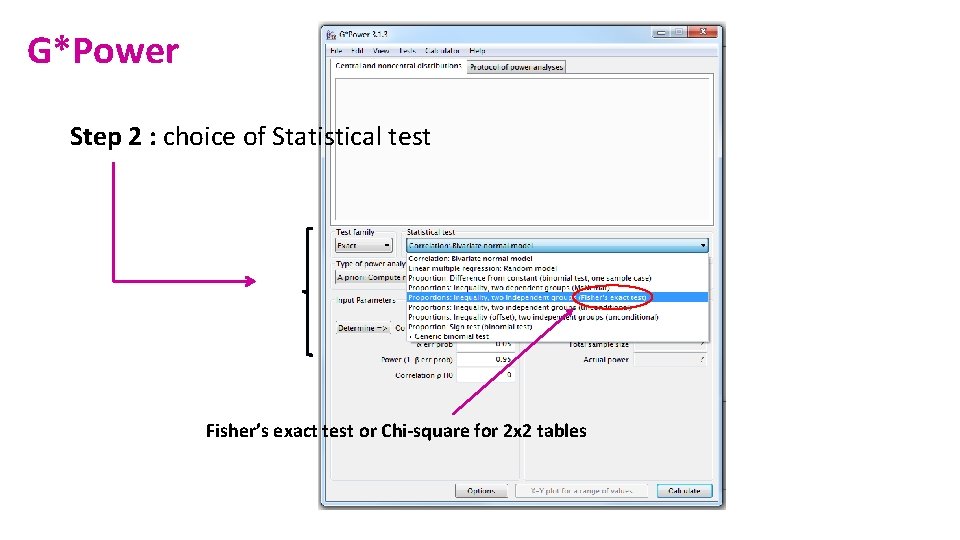
G*Power Step 2 : choice of Statistical test Fisher’s exact test or Chi-square for 2 x 2 tables

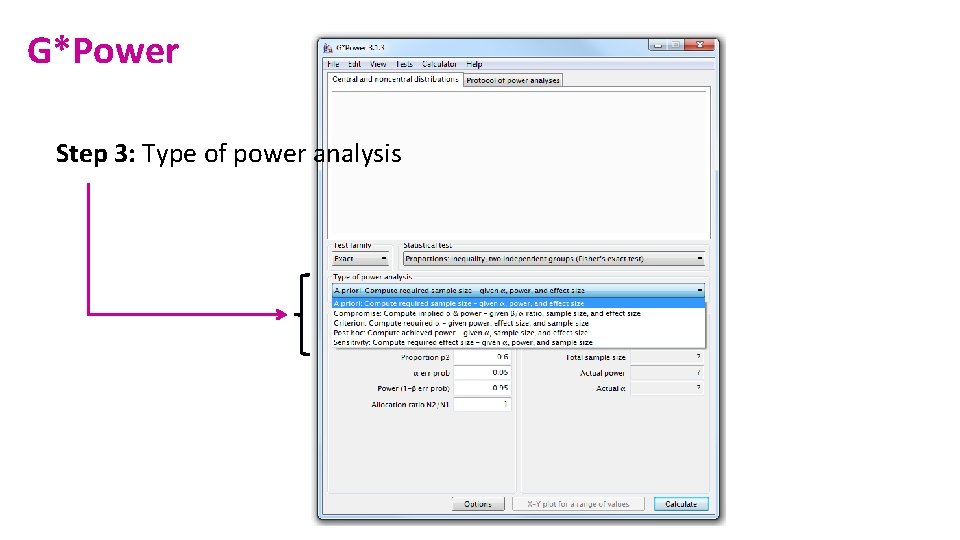
G*Power Step 3: Type of power analysis

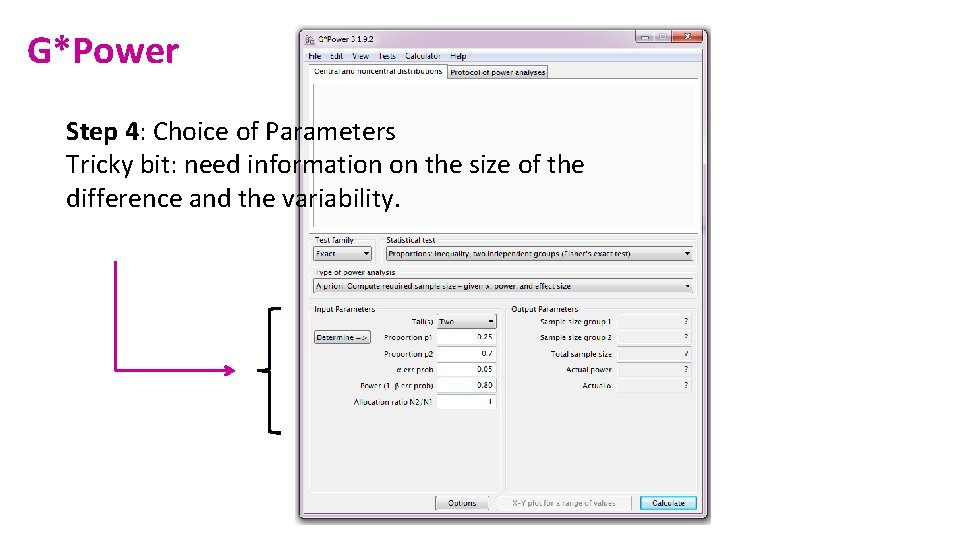
G*Power Step 4: Choice of Parameters Tricky bit: need information on the size of the difference and the variability.

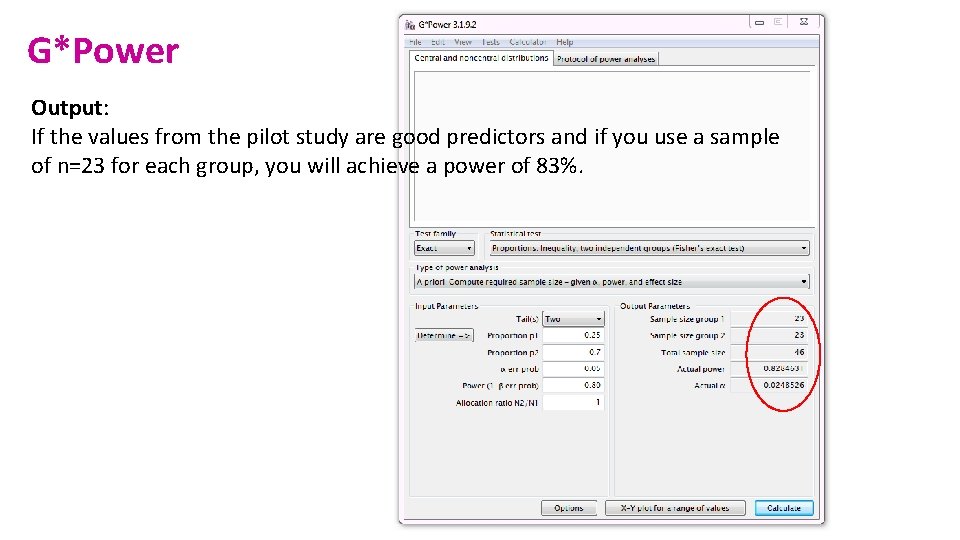
G*Power Output: If the values from the pilot study are good predictors and if you use a sample of n=23 for each group, you will achieve a power of 83%.

Chi-square and Fisher’s tests • Chi 2 test very easy to calculate by hand but Fisher’s very hard • Many software will not perform a Fisher’s test on tables > 2 x 2 • • Fisher’s test more accurate than Chi 2 test on small samples Chi 2 test more accurate than Fisher’s test on large samples • Chi 2 test assumptions: • 2 x 2 table: no expected count <5 • Bigger tables: all expected > 1 and no more than 20% < 5 • Yates’s continuity correction • All statistical tests work well when their assumptions are met • When not: probability Type 1 error increases • Solution: corrections that increase p-values • Corrections are dangerous: no magic • Probably best to avoid them

Chi-square test • In a chi-square test, the observed frequencies for two or more groups are compared with expected frequencies by chance. • With observed frequency = collected data • Example with ‘cats and dogs’

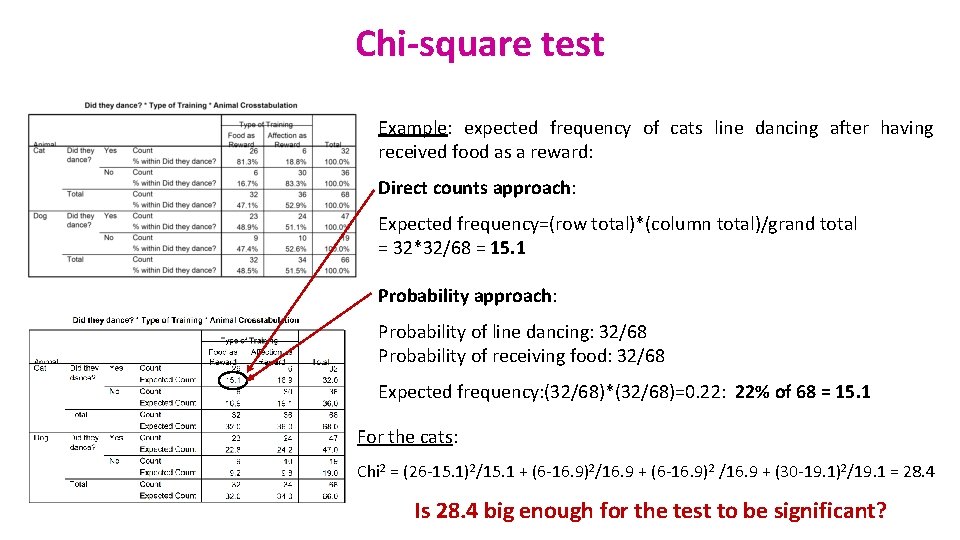
Chi-square test Example: expected frequency of cats line dancing after having received food as a reward: Direct counts approach: Expected frequency=(row total)*(column total)/grand total = 32*32/68 = 15. 1 Probability approach: Probability of line dancing: 32/68 Probability of receiving food: 32/68 Expected frequency: (32/68)*(32/68)=0. 22: 22% of 68 = 15. 1 For the cats: Chi 2 = (26 -15. 1)2/15. 1 + (6 -16. 9)2/16. 9 + (6 -16. 9)2 /16. 9 + (30 -19. 1)2/19. 1 = 28. 4 Is 28. 4 big enough for the test to be significant?

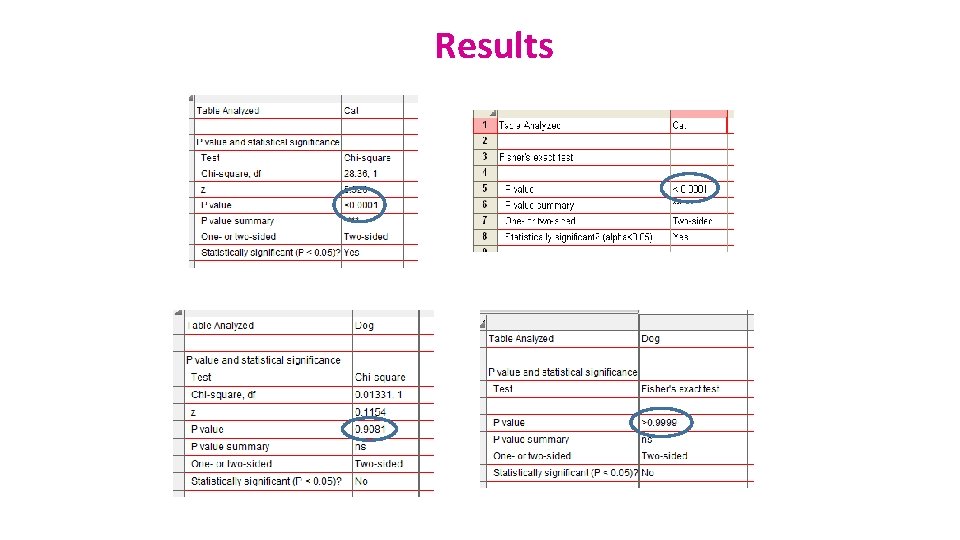
Results

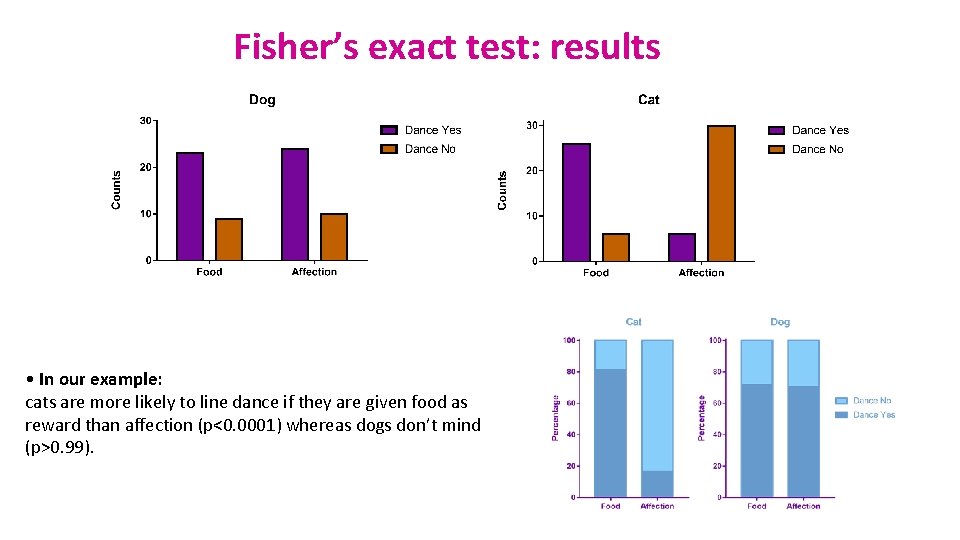
Fisher’s exact test: results • In our example: cats are more likely to line dance if they are given food as reward than affection (p<0. 0001) whereas dogs don’t mind (p>0. 99).

Quantitative data

Quantitative data • They take numerical values (units of measurement) • Discrete: obtained by counting • Example: number of students in a class • values vary by finite specific steps • or continuous: obtained by measuring • Example: height of students in a class • any values • They can be described by a series of parameters: • Mean, variance, standard deviation, standard error and confidence interval

Measures of central tendency Mode and Median • Mode: most commonly occurring value in a distribution • Median: value exactly in the middle of an ordered set of numbers

Measures of central tendency Mean • Definition: average of all values in a column • It can be considered as a model because it summaries the data • Example: a group of 5 lecturers: number of friends of each members of the group: 1, 2, 3, 3 and 4 • Mean: (1+2+3+3+4)/5 = 2. 6 friends person • Clearly an hypothetical value • How can we know that it is an accurate model? • Difference between the real data and the model created

Measures of dispersion • From Field, 2000

Sum of Squared errors (SS) •

Variance and standard deviation •

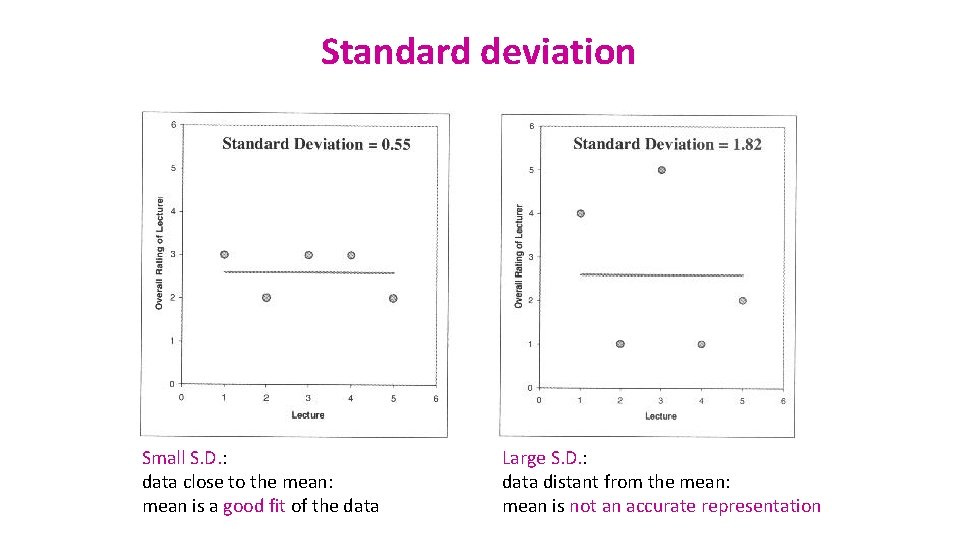
Standard deviation Small S. D. : data close to the mean: mean is a good fit of the data Large S. D. : data distant from the mean: mean is not an accurate representation

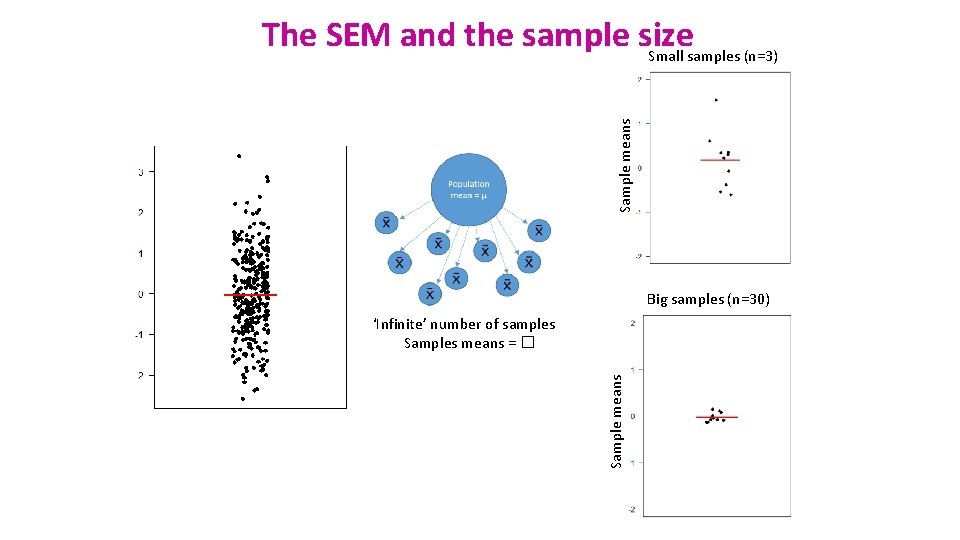
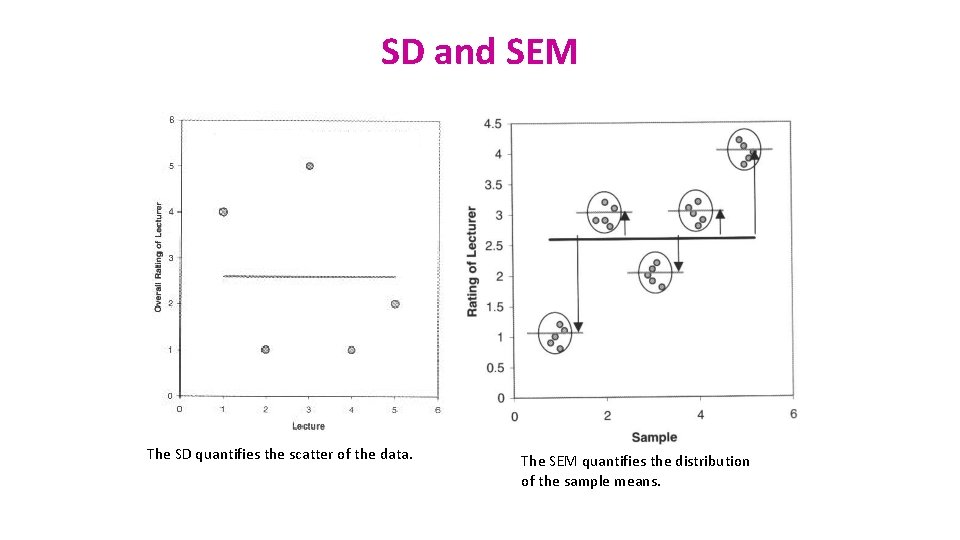
SD and SEM (SEM = SD/√N) • What are they about? • The SD quantifies how much the values vary from one another: scatter or spread • The SD does not change predictably as you acquire more data. • The SEM quantifies how accurately you know the true mean of the population. • Why? Because it takes into account: SD + sample size • The SEM gets smaller as your sample gets larger • Why? Because the mean of a large sample is likely to be closer to the true mean than is the mean of a small sample.

The SEM and the sample size A population

Sample means The SEM and the sample size Small samples (n=3) Big samples (n=30) Sample means ‘Infinite’ number of samples Samples means = �

SD and SEM The SD quantifies the scatter of the data. The SEM quantifies the distribution of the sample means.

SD or SEM ? • If the scatter is caused by biological variability, it is important to show the variation. • Report the SD rather than the SEM. • Better even: show a graph of all data points. • If you are using an in vitro system with no biological variability, the scatter is about experimental imprecision (no biological meaning). • Report the SEM to show well you have determined the mean.

Confidence interval • Range of values that we can be 95% confident contains the true mean of the population. - So limits of 95% CI: [Mean - 1. 96 SEM; Mean + 1. 96 SEM] (SEM = SD/√N) Error bars Type Description Standard deviation Descriptive Typical or average difference between the data points and their mean. Standard error Inferential A measure of how variable the mean will be, if you repeat the whole study many times. Confidence interval usually 95% CI Inferential A range of values you can be 95% confident contains the true mean.

Analysis of Quantitative Data • Choose the correct statistical test to answer your question: • They are 2 types of statistical tests: • Parametric tests with 4 assumptions to be met by the data, • Non-parametric tests with no or few assumptions (e. g. Mann-Whitney test) and/or for qualitative data (e. g. Fisher’s exact and χ2 tests).

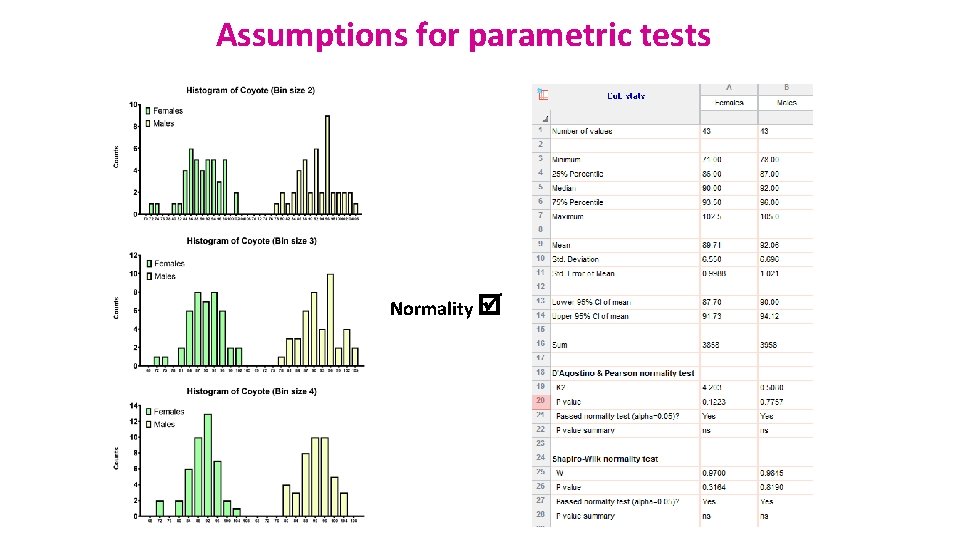
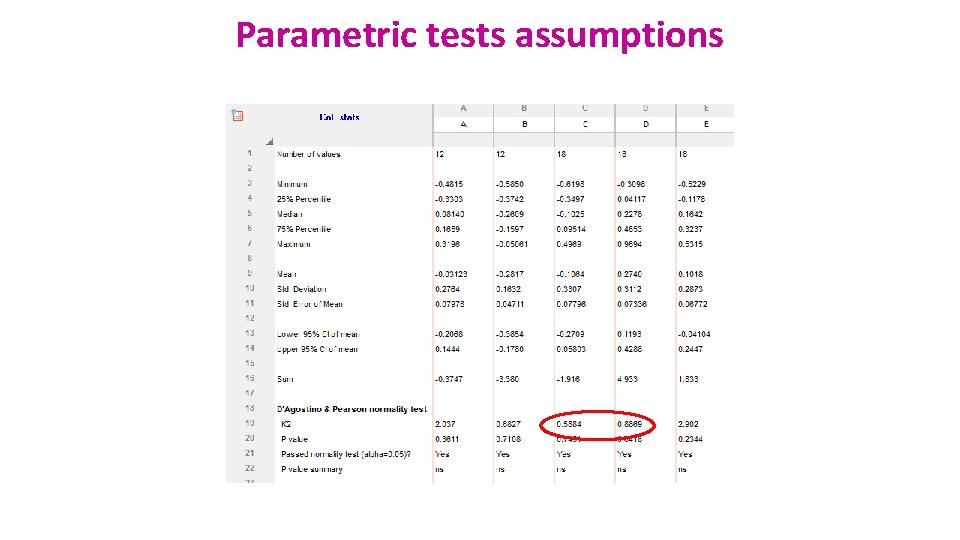
Assumptions of Parametric Data • All parametric tests have 4 basic assumptions that must be met for the test to be accurate. 1) Normally distributed data • Normal shape, bell shape, Gaussian shape • Transformations can be made to make data suitable for parametric analysis.

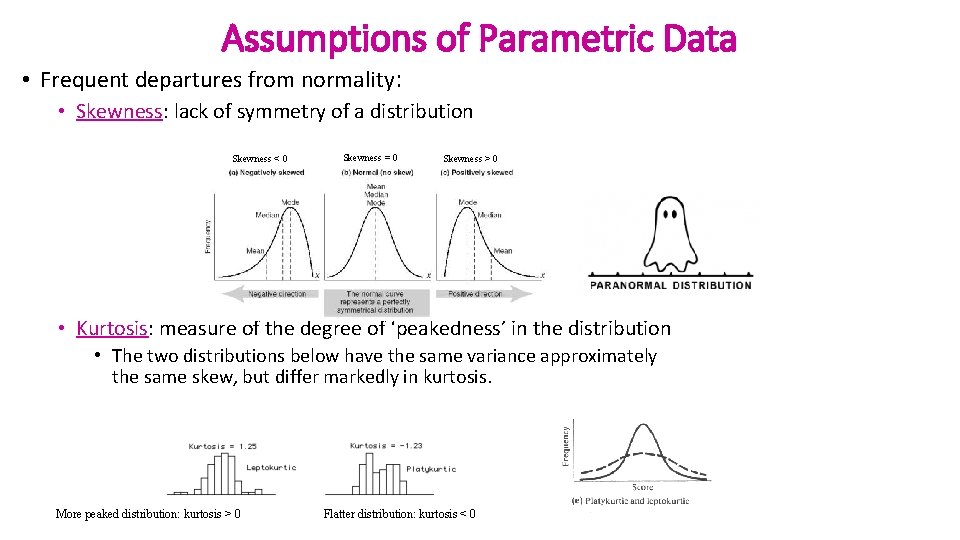
Assumptions of Parametric Data • Frequent departures from normality: • Skewness: lack of symmetry of a distribution Skewness < 0 Skewness = 0 Skewness > 0 • Kurtosis: measure of the degree of ‘peakedness’ in the distribution • The two distributions below have the same variance approximately the same skew, but differ markedly in kurtosis. More peaked distribution: kurtosis > 0 Flatter distribution: kurtosis < 0

Assumptions of Parametric Data 2) Homogeneity in variance • The variance should not change systematically throughout the data 3) Interval data (linearity) • The distance between points of the scale should be equal at all parts along the scale. 4) Independence • Data from different subjects are independent • Values corresponding to one subject do not influence the values corresponding to another subject. • Important in repeated measures experiments

Analysis of Quantitative Data • Is there a difference between my groups regarding the variable I am measuring? • e. g. are the mice in the group A heavier than those in group B? • Tests with 2 groups: • Parametric: Student’s t-test • Non parametric: Mann-Whitney/Wilcoxon rank sum test • Tests with more than 2 groups: • Parametric: Analysis of variance (one-way ANOVA) • Non parametric: Kruskal Wallis • Is there a relationship between my 2 (continuous) variables? • e. g. is there a relationship between the daily intake in calories and an increase in body weight? • Test: Correlation (parametric) and curve fitting

Sample Difference Statistical inference Meaningful? Yes Population Real? Statistical test Statistic Big enough? e. g. t, F … = Difference + Noise + Sample

Signal-to-noise ratio • Stats are all about understanding and controlling variation. Difference + Noise signal noise If the noise is low then the signal is detectable … = statistical significance signal noise … but if the noise (i. e. interindividual variation) is large then the same signal will not be detected = no statistical significance • In a statistical test, the ratio of signal to noise determines the significance.

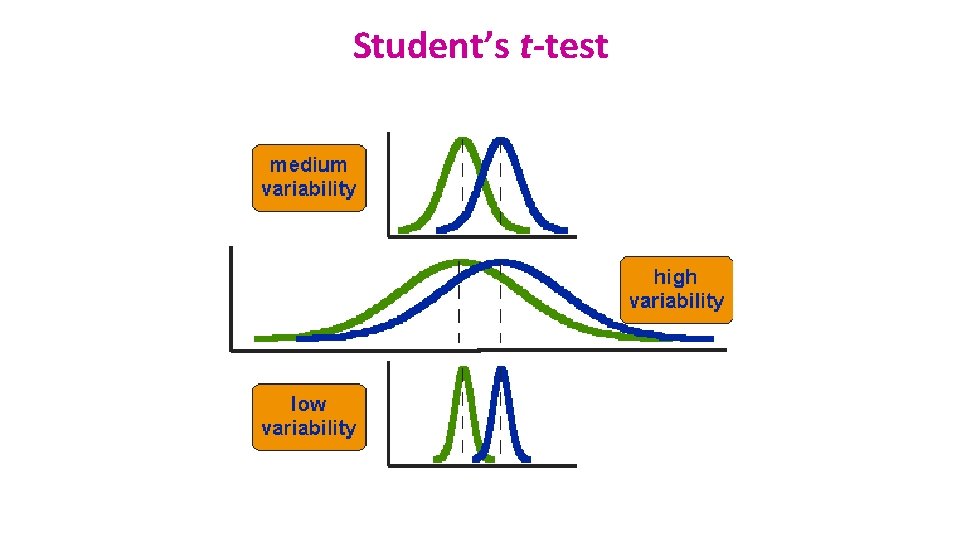
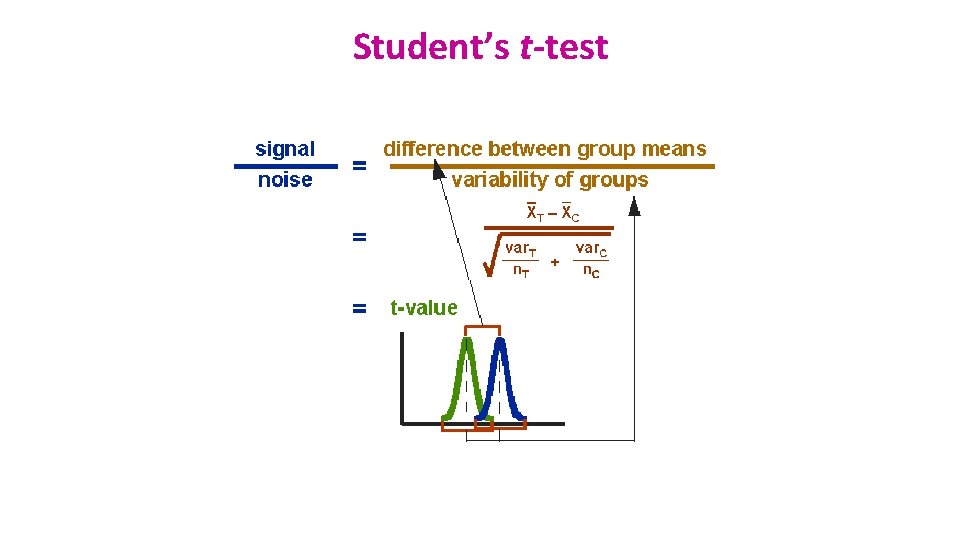
Comparison between 2 groups: Student’s t-test • Basic idea: • When we are looking at the differences between scores for 2 groups, we have to judge the difference between their means relative to the spread or variability of their scores. • Eg: comparison of 2 groups: control and treatment

Student’s t-test

Student’s t-test

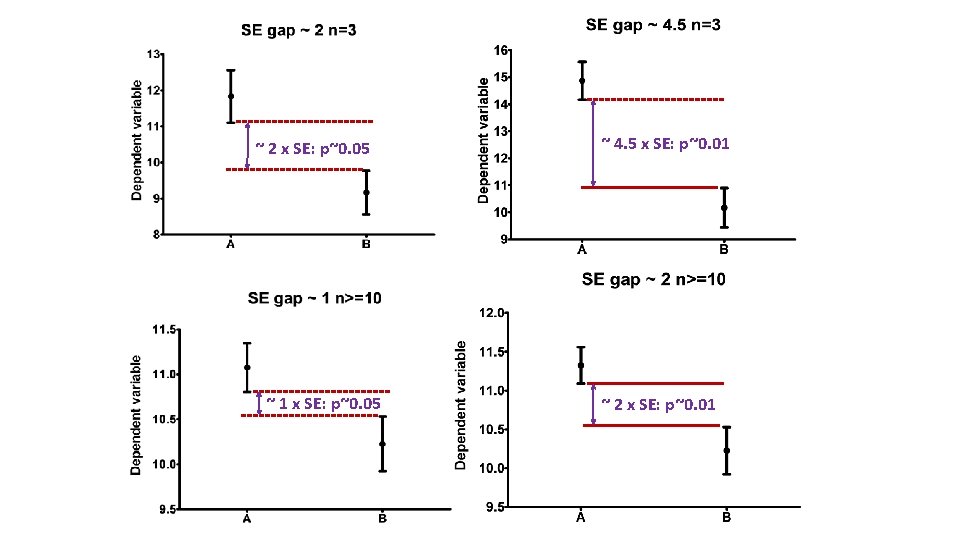
~ 2 x SE: p~0. 05 ~ 1 x SE: p~0. 05 ~ 4. 5 x SE: p~0. 01 ~ 2 x SE: p~0. 01

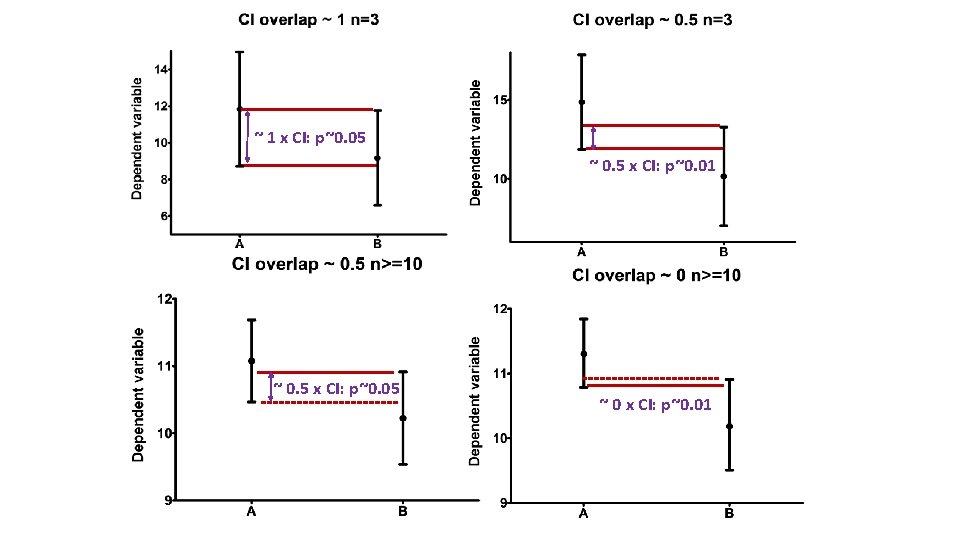
~ 1 x CI: p~0. 05 ~ 0. 5 x CI: p~0. 01 ~ 0. 5 x CI: p~0. 05 ~ 0 x CI: p~0. 01

Student’s t-test • 3 types: • Independent t-test • compares means for two independent groups of cases. • Paired t-test • looks at the difference between two variables for a single group: • the second ‘sample’ of values comes from the same subjects (mouse, petri dish …). • One-Sample t-test • tests whether the mean of a single variable differs from a specified constant (often 0)

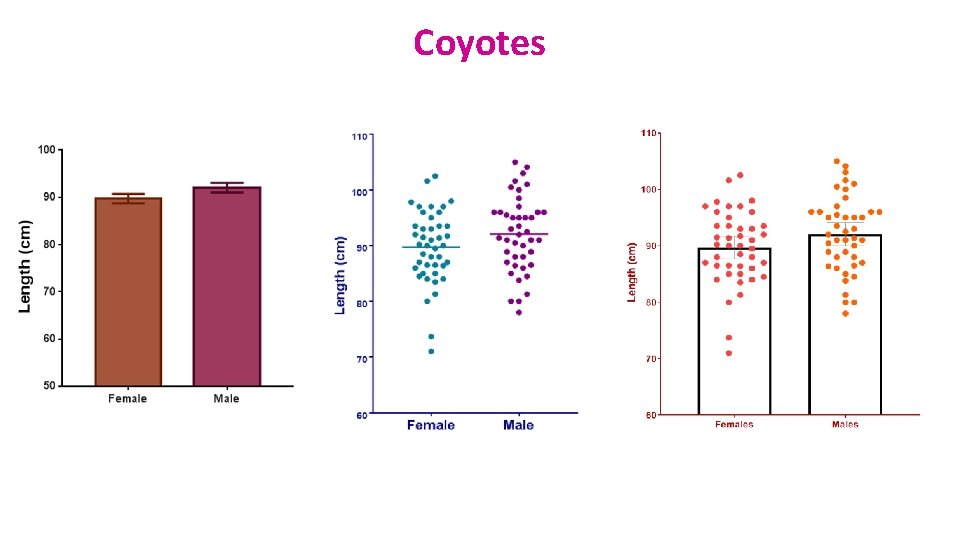
Example: coyotes. xlsx • Question: do male and female coyotes differ in size? • Sample size • Data exploration • Check the assumptions for parametric test • Statistical analysis: Independent t-test

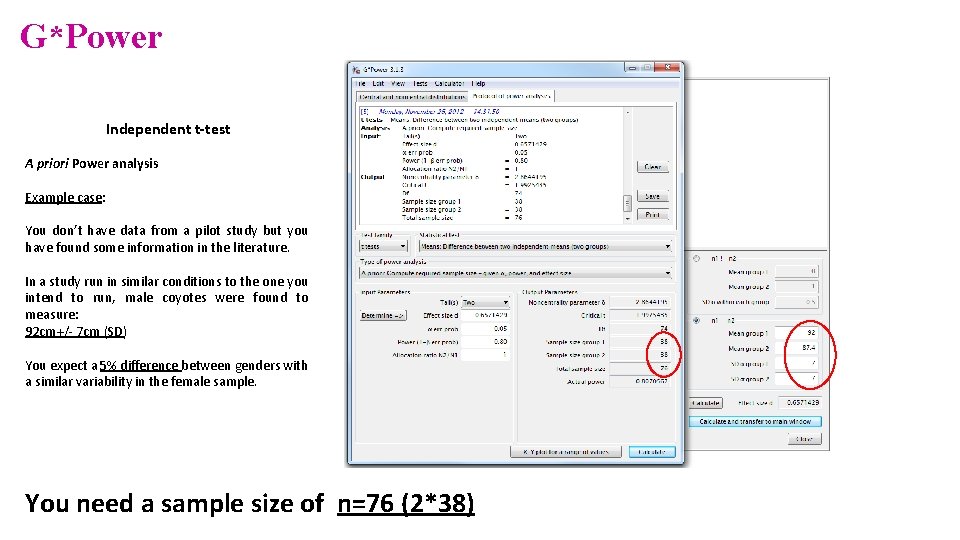
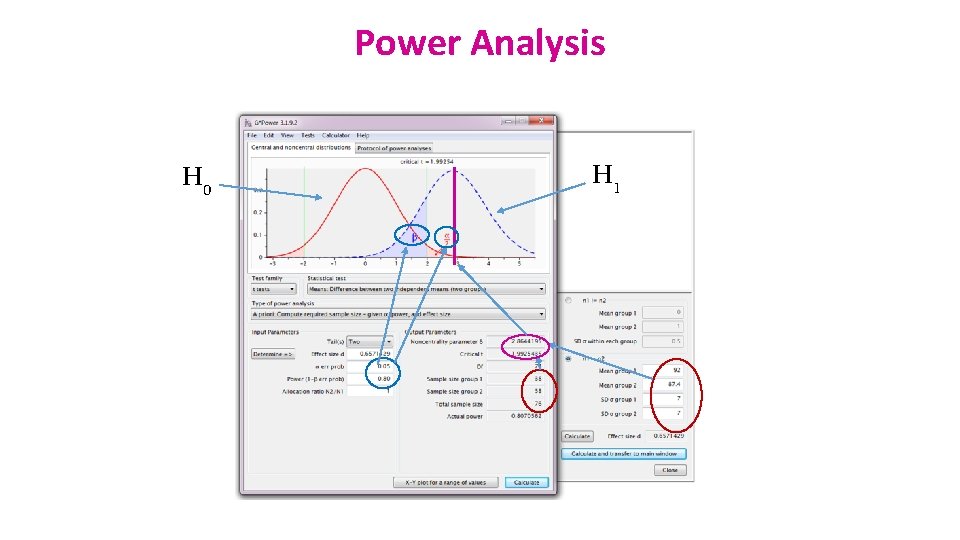
Power analysis • Example case: No data from a pilot study but we have found some information in the literature. In a study run in similar conditions as in the one we intend to run, male coyotes were found to measure: 92 cm+/- 7 cm (SD). We expect a 5% difference between genders. • smallest biologically meaningful difference

G*Power Independent t-test A priori Power analysis Example case: You don’t have data from a pilot study but you have found some information in the literature. In a study run in similar conditions to the one you intend to run, male coyotes were found to measure: 92 cm+/- 7 cm (SD) You expect a 5% difference between genders with a similar variability in the female sample. You need a sample size of n=76 (2*38)

Power Analysis

Power Analysis H 0 H 1

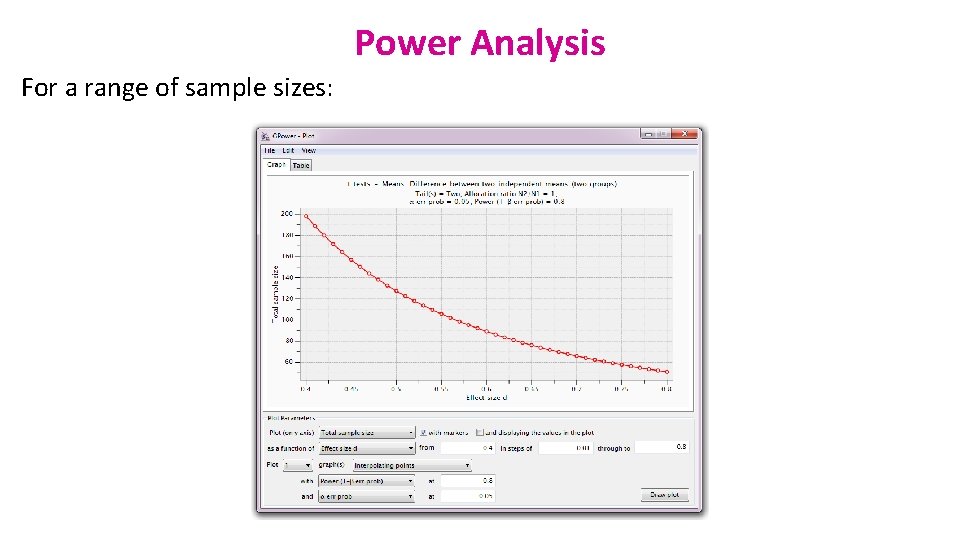
Power Analysis For a range of sample sizes:

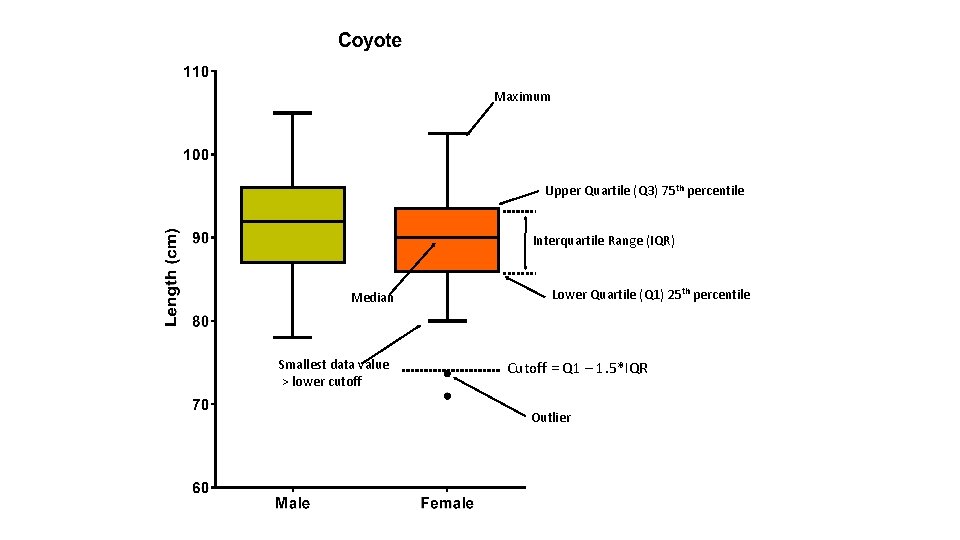
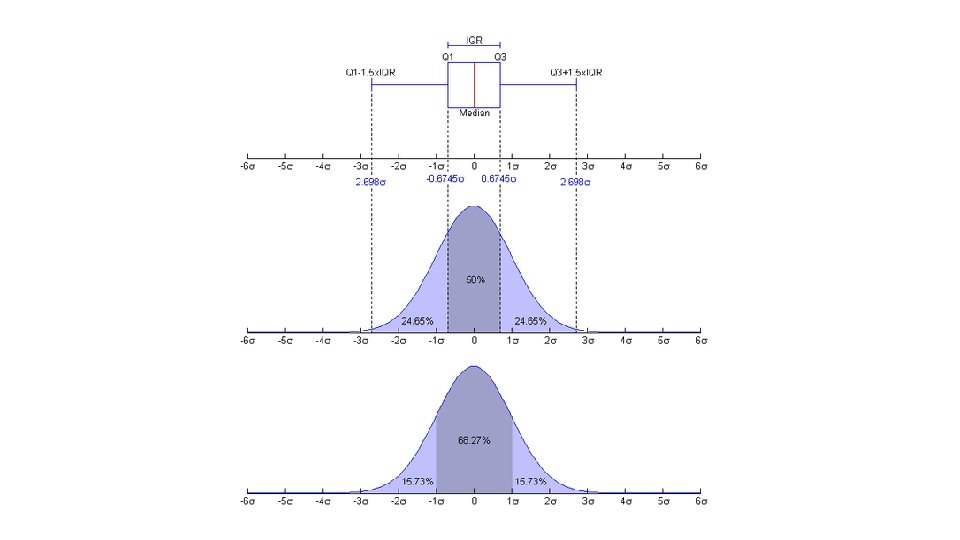
Maximum Upper Quartile (Q 3) 75 th percentile Interquartile Range (IQR) Median Smallest data value > lower cutoff Lower Quartile (Q 1) 25 th percentile Cutoff = Q 1 – 1. 5*IQR Outlier

Assumptions for parametric tests Normality

Coyotes

Independent t-test: results Males tend to be longer than females but not significantly so (p=0. 1045) Homogeneity in variance What about the power of the analysis?

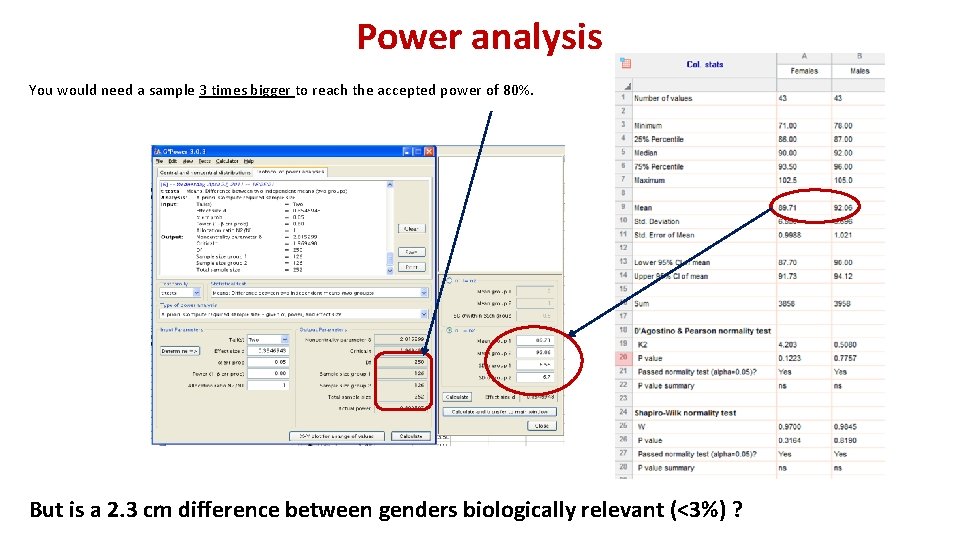
Power analysis You would need a sample 3 times bigger to reach the accepted power of 80%. But is a 2. 3 cm difference between genders biologically relevant (<3%) ?

The sample size: the bigger the better? • It takes huge samples to detect tiny differences but tiny samples to detect huge differences. • What if the tiny difference is meaningless? • Beware of overpower • Nothing wrong with the stats: it is all about interpretation of the results of the test. • Remember the important first step of power analysis • What is the effect size of biological interest?

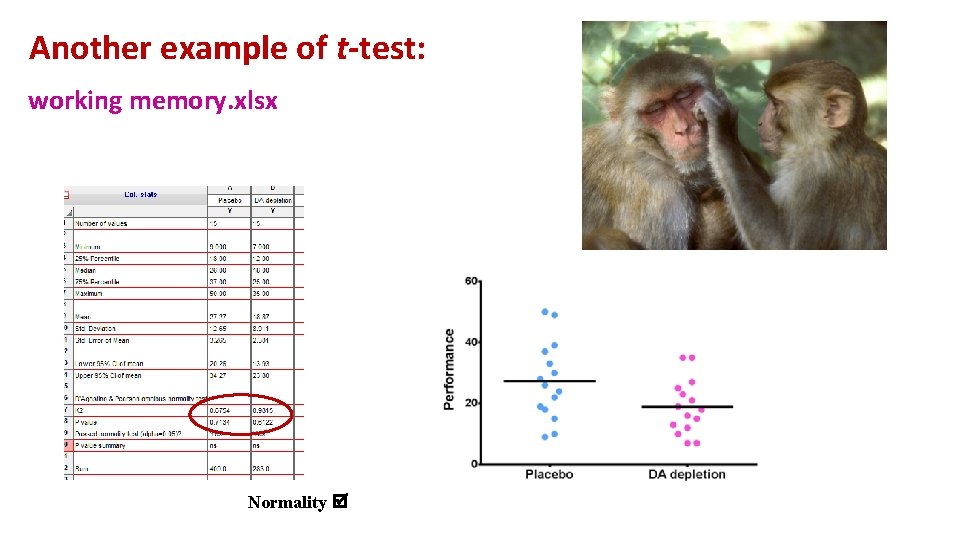
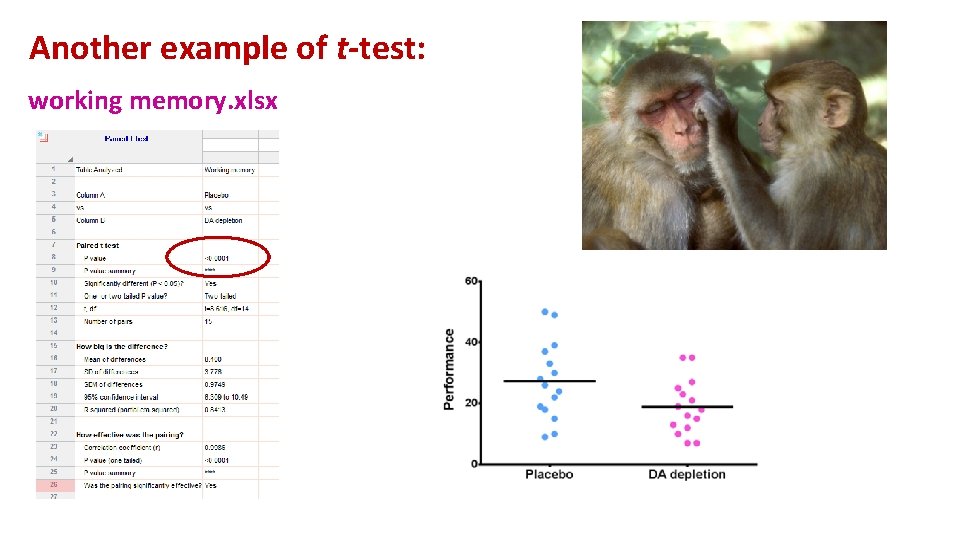
Another example of t-test: working memory. xlsx A group of rhesus monkeys (n=15) performs a task involving memory after having received a placebo. Their performance is graded on a scale from 0 to 100. They are then asked to perform the same task after having received a dopamine depleting agent. Is there an effect of treatment on the monkeys' performance?

Another example of t-test: working memory. xlsx Normality

Another example of t-test: working memory. xlsx

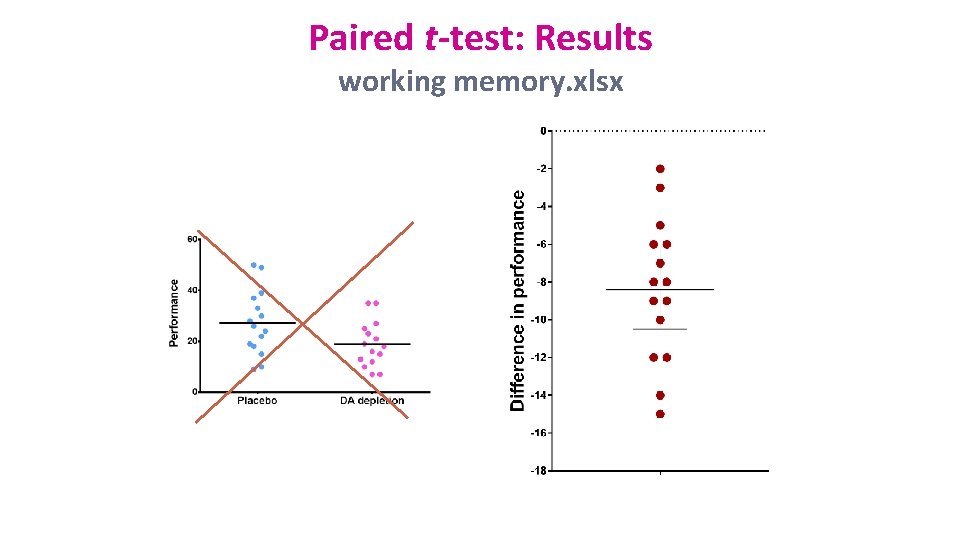
Paired t-test: Results working memory. xlsx

Comparison of more than 2 means • Running multiple tests on the same data increases the familywise error rate. • What is the familywise error rate? – The error rate across tests conducted on the same experimental data. • One of the basic rules (‘laws’) of probability: – The Multiplicative Rule: The probability of the joint occurrence of 2 or more independent events is the product of the individual probabilities.

Familywise error rate • Example: All pairwise comparisons between 3 groups A, B and C: – A-B, A-C and B-C • Probability of making the Type I Error: 5% – The probability of not making the Type I Error is 95% (=1 – 0. 05) • Multiplicative Rule: – Overall probability of no Type I errors is: 0. 95 * 0. 95 = 0. 857 • So the probability of making at least one Type I Error is 1 -0. 857 = 0. 143 or 14. 3% • The probability has increased from 5% to 14. 3% • Comparisons between 5 groups instead of 3, the familywise error rate is 40% (=1 -(0. 95)n)

Familywise error rate • Solution to the increase of familywise error rate: correction for multiple comparisons – Post-hoc tests • Many different ways to correct for multiple comparisons: – Different statisticians have designed corrections addressing different issues • e. g. unbalanced design, heterogeneity of variance, liberal vs conservative • However, they all have one thing in common: – the more tests, the higher the familywise error rate: the more stringent the correction • Tukey, Bonferroni, Sidak, Benjamini-Hochberg … – Two ways to address the multiple testing problem • Familywise Error Rate (FWER) vs. False Discovery Rate (FDR)

Multiple testing problem • FWER: Bonferroni: αadjust = 0. 05/n comparisons e. g. 3 comparisons: 0. 05/3=0. 016 – Problem: very conservative leading to loss of power (lots of false negative) – 10 comparisons: threshold for significance: 0. 05/10: 0. 005 – Pairwise comparisons across 20. 000 genes • FDR: Benjamini-Hochberg: the procedure controls the expected proportion of “discoveries” (significant tests) that are false (false positive). – Less stringent control of Type I Error than FWER procedures which control the probability of at least one Type I Error – More power at the cost of increased numbers of Type I Errors. • Difference between FWER and FDR: – a p-value of 0. 05 implies that 5% of all tests will result in false positives. – a FDR adjusted p-value (or q-value) of 0. 05 implies that 5% of significant tests will result in false positives.

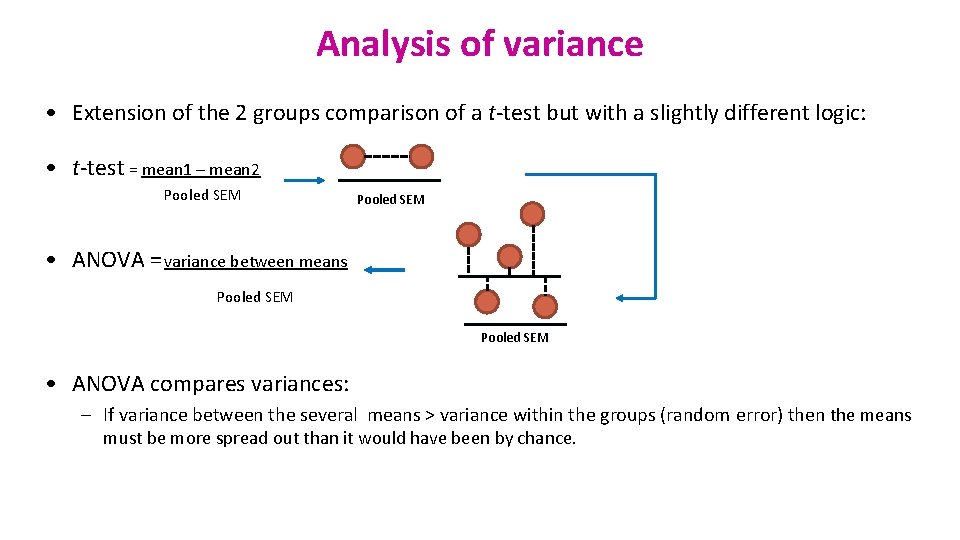
Analysis of variance • Extension of the 2 groups comparison of a t-test but with a slightly different logic: • t-test = mean 1 – mean 2 Pooled SEM • ANOVA = variance between means Pooled SEM • ANOVA compares variances: – If variance between the several means > variance within the groups (random error) then the means must be more spread out than it would have been by chance.

Analysis of variance • The statistic for ANOVA is the F ratio. • F = Variance between the groups Variance within the groups (individual variability) Variation explained by the model (= systematic) Variation explained by unsystematic factors (= random variation) • If the variance amongst sample means is greater than the error/random variance, then F>1 – In an ANOVA, we test whether F is significantly higher than 1 or not.

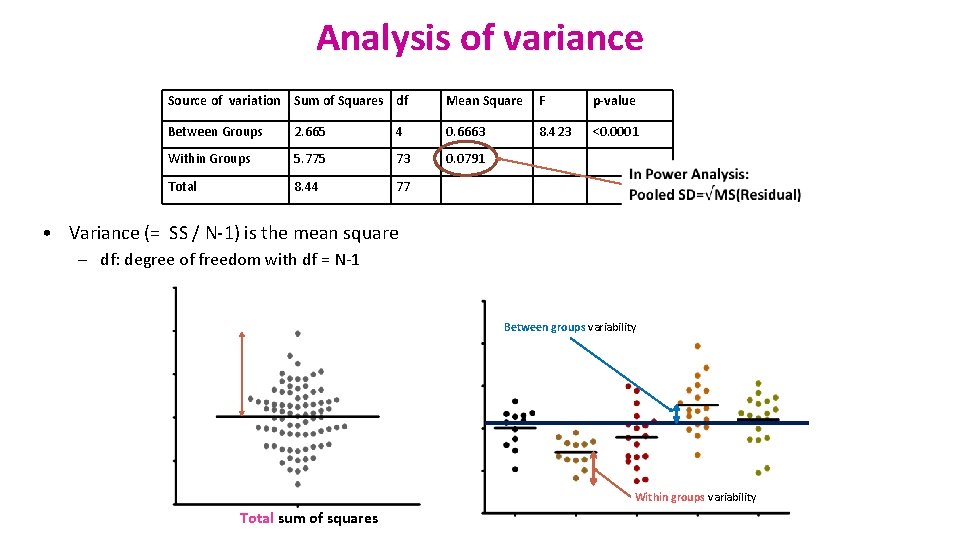
Analysis of variance Source of variation Sum of Squares df Mean Square F p-value Between Groups 2. 665 4 0. 6663 8. 423 <0. 0001 Within Groups 5. 775 73 0. 0791 Total 8. 44 77 • Variance (= SS / N-1) is the mean square – df: degree of freedom with df = N-1 Between groups variability Within groups variability Total sum of squares

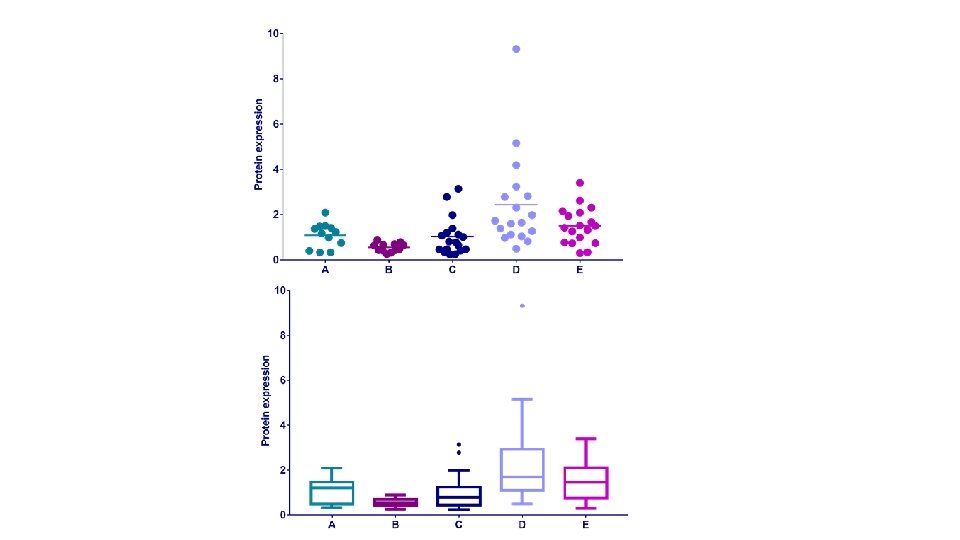
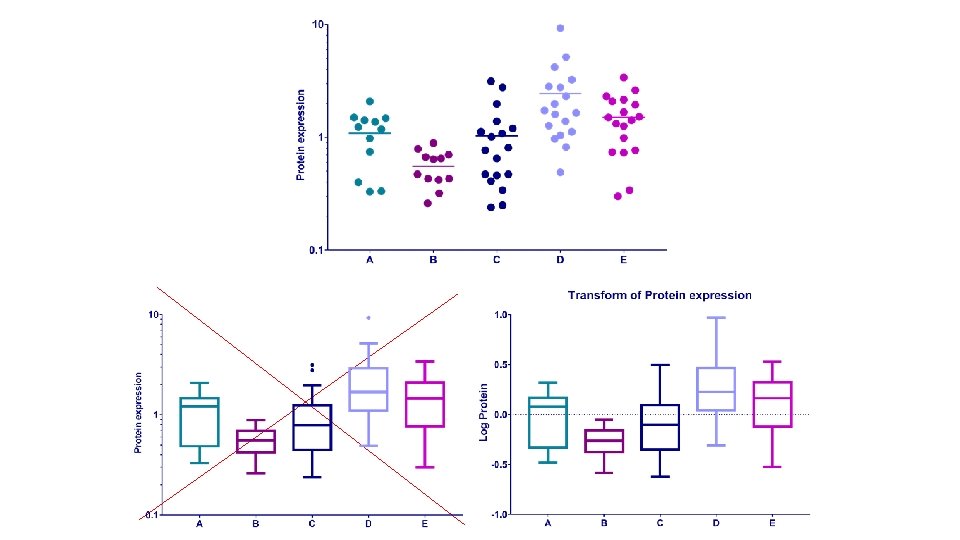
Example: protein. expression. csv • Question: is there a difference in protein expression between the 5 cell lines? • 1 Plot the data • 2 Check the assumptions for parametric test • 3 Statistical analysis: ANOVA

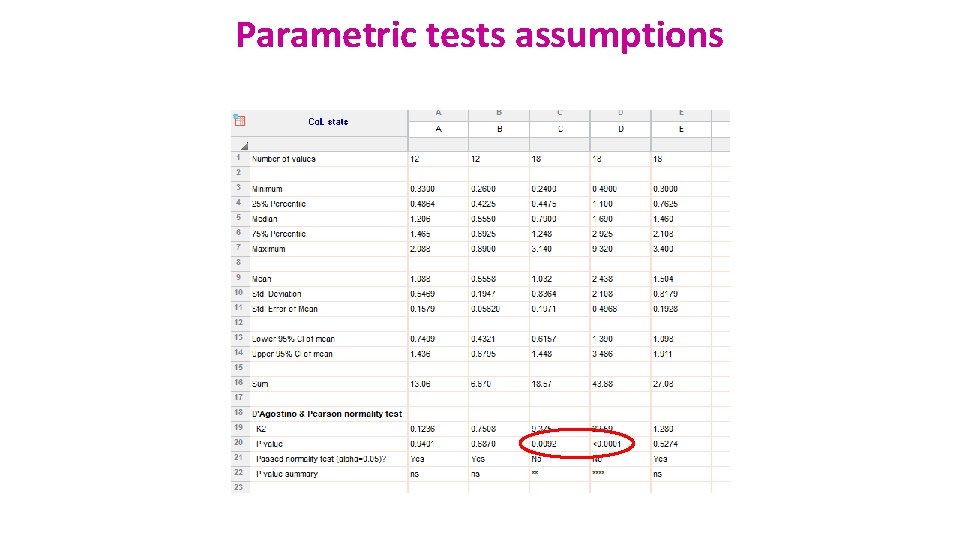
Parametric tests assumptions

Parametric tests assumptions

Analysis of variance: Post hoc tests • The ANOVA is an “omnibus” test: it tells you that there is (or not) a difference between your means but not exactly which means are significantly different from which other ones. – To find out, you need to apply post hoc tests. – These post hoc tests should only be used when the ANOVA finds a significant effect.

Analysis of variancec

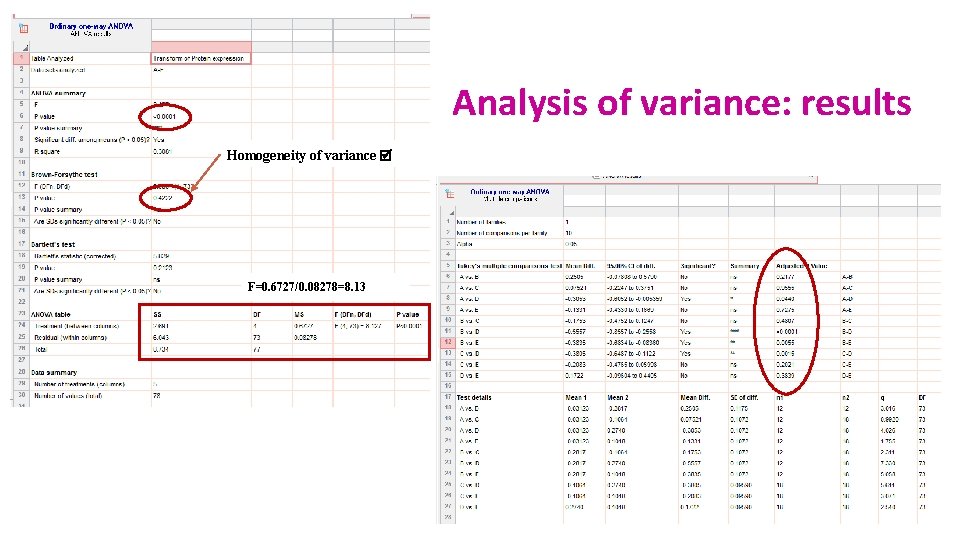
Analysis of variance: results Homogeneity of variance F=0. 6727/0. 08278=8. 13

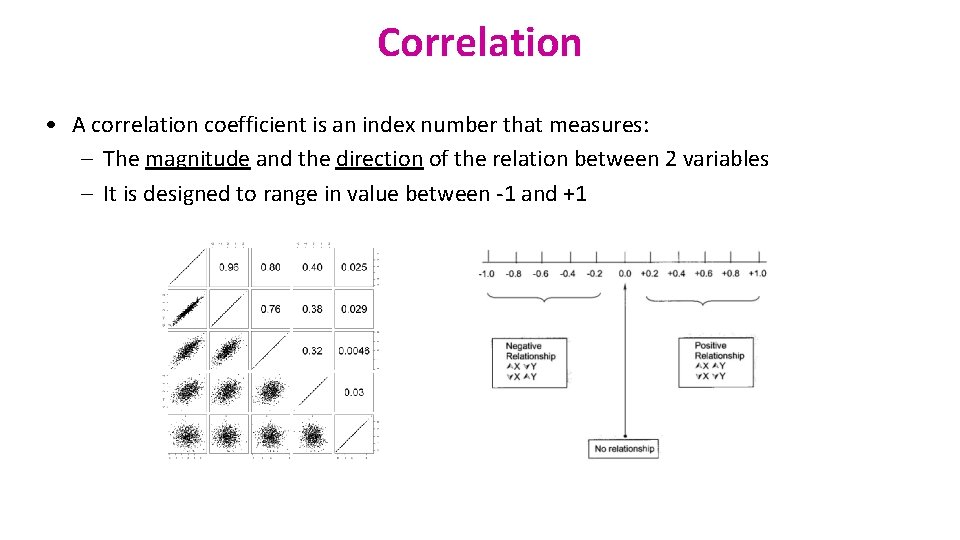
Correlation • A correlation coefficient is an index number that measures: – The magnitude and the direction of the relation between 2 variables – It is designed to range in value between -1 and +1

Correlation • Most widely-used correlation coefficient: – Pearson product-moment correlation coefficient “r” • The 2 variables do not have to be measured in the same units but they have to be proportional (meaning linearly related) – Coefficient of determination: • r is the correlation between X and Y • r 2 is the coefficient of determination: – It gives you the proportion of variance in Y that can be explained by X, in percentage.

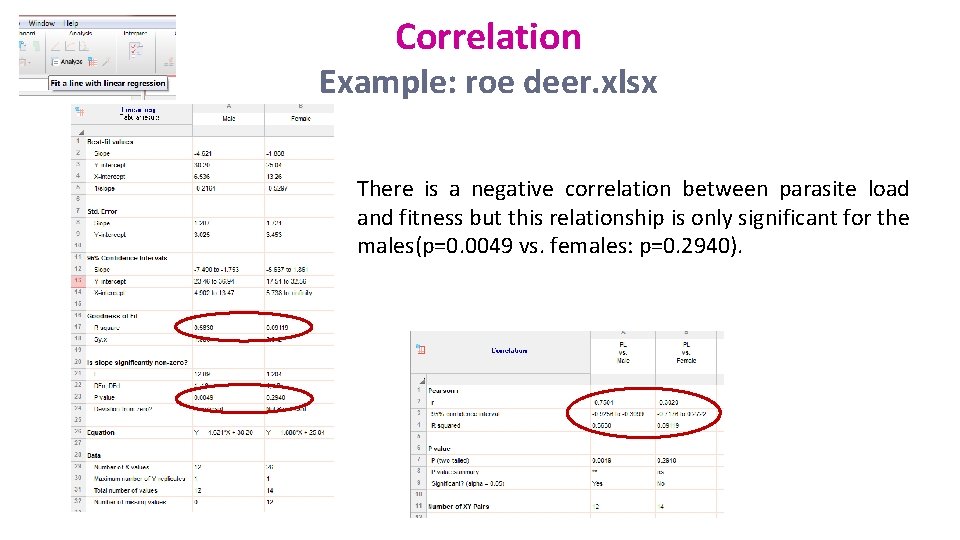
Correlation Example: roe deer. xlsx • Is there a relationship between parasite burden and body mass in roe deer?

Correlation Example: roe deer. xlsx There is a negative correlation between parasite load and fitness but this relationship is only significant for the males(p=0. 0049 vs. females: p=0. 2940).

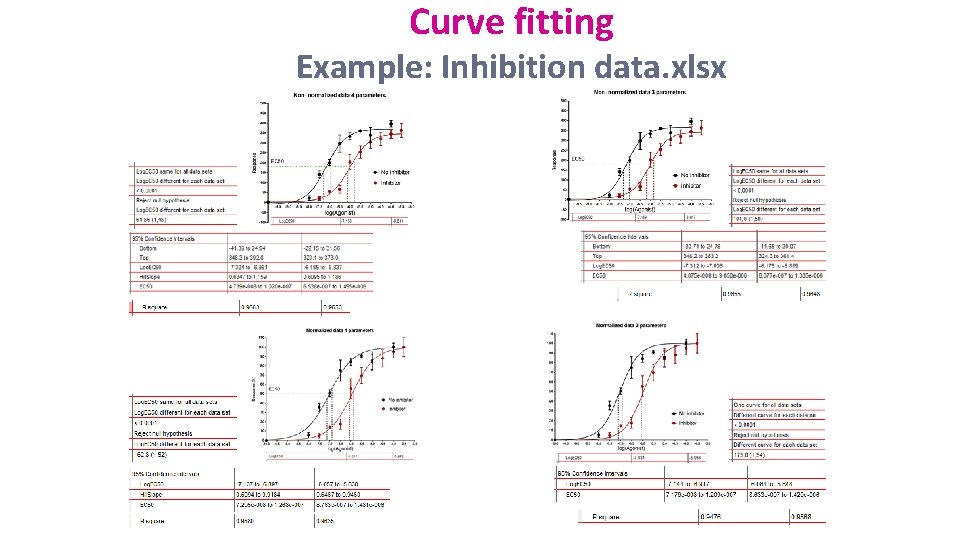
• Dose-response curves Curve fitting – Nonlinear regression – Dose-response experiments typically use around 5 -10 doses of agonist, equally spaced on a logarithmic scale – Y values are responses • The aim is often to determine the IC 50 or the EC 50 – IC 50 (I=Inhibition): concentration of an agonist that provokes a response half way between the maximal (Top) response and the maximally inhibited (Bottom) response. – EC 50 (E=Effective): concentration that gives half-maximal response Stimulation: Y=Bottom + (Top-Bottom)/(1+10^((Log. EC 50 -X)*Hill. Slope)) Inhibition: Y=Bottom + (Top-Bottom)/(1+10^((X-Log. IC 50)))

Curve fitting Example: Inhibition data. xlsx Step by step analysis and considerations: 1 - Choose a Model: not necessary to normalise should choose it when values defining 0 and 100 are precise variable slope better if plenty of data points (variable slope or 4 parameters) 2 - Choose a Method: outliers, fitting method, weighting method and replicates 3 - Compare different conditions: Diff in parameters Diff between conditions for one or more parameters Constraint vs no constraint Diff between conditions for one or more parameters 4 - Constrain: depends on your experiment depends if your data don’t define the top or the bottom of the curve

Curve fitting Example: Inhibition data. xlsx Step by step analysis and considerations: 5 - Initial values: defaults usually OK unless the fit looks funny 6 - Range: defaults usually OK unless you are not interested in the x-variable full range (ie time) 7 - Output: summary table presents same results in a … summarized way. 8 – Confidence: calculate and plot confidence intervals 9 - Diagnostics: check for normality (weights) and outliers (but keep them in the analysis) check Replicates test residual plots

Curve fitting Example: Inhibition data. xlsx

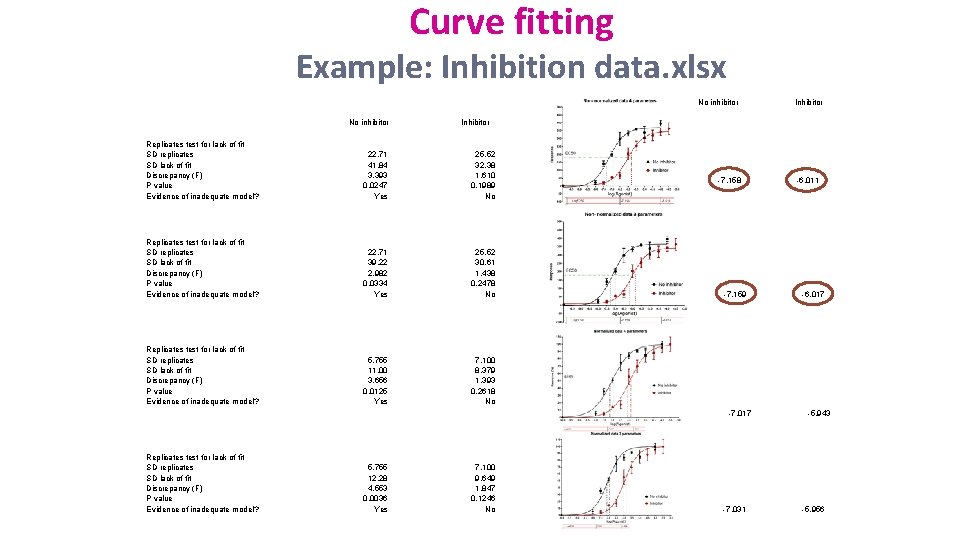
Curve fitting Example: Inhibition data. xlsx No inhibitor Inhibitor Replicates test for lack of fit SD replicates SD lack of fit Discrepancy (F) P value Evidence of inadequate model? 22. 71 41. 84 3. 393 0. 0247 Yes 25. 52 32. 38 1. 610 0. 1989 No Replicates test for lack of fit SD replicates SD lack of fit Discrepancy (F) P value Evidence of inadequate model? 22. 71 39. 22 2. 982 0. 0334 Yes 25. 52 30. 61 1. 438 0. 2478 No Replicates test for lack of fit SD replicates SD lack of fit Discrepancy (F) P value Evidence of inadequate model? 5. 755 11. 00 3. 656 0. 0125 Yes 7. 100 8. 379 1. 393 0. 2618 No -7. 158 -7. 159 -7. 017 Replicates test for lack of fit SD replicates SD lack of fit Discrepancy (F) P value Evidence of inadequate model? 5. 755 12. 28 4. 553 0. 0036 Yes Inhibitor 7. 100 9. 649 1. 847 0. 1246 No -7. 031 -6. 017 -5. 943 -5. 956

My email address if you need some help with Graph. Pad: anne. segonds-pichon@babraham. ac. uk Slides and manual available on: https: //www. bioinformatics. babraham. ac. uk/training. html